 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
約数の和 愛知高校

単元:
#計算と数の性質#数学(中学生)#約数・倍数を利用する問題#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
p,qは素数。積pqの正の約数の和が18のとき
pq=?
愛知高等学校
この動画を見る
p,qは素数。積pqの正の約数の和が18のとき
pq=?
愛知高等学校
【まず手を動かそう】一次関数:駿台甲府高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
xについての方程式$ 4+5(a-2x)=a-2x $の解が$ x=1 $であるとき,
$ a $の値を求めよ.
駿台甲府高校過去問
この動画を見る
xについての方程式$ 4+5(a-2x)=a-2x $の解が$ x=1 $であるとき,
$ a $の値を求めよ.
駿台甲府高校過去問
東大寺学園の因数分解

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$x^2(y^3-2y^2)-5x(y^2-2y)+4y-8$
東大寺学園高等学校
この動画を見る
因数分解せよ
$x^2(y^3-2y^2)-5x(y^2-2y)+4y-8$
東大寺学園高等学校
東大寺学園の因数分解

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$(x^2-2x)^2 + 4(x^2 - 2x) + 3$
東大寺学園高等学校
この動画を見る
因数分解せよ
$(x^2-2x)^2 + 4(x^2 - 2x) + 3$
東大寺学園高等学校
【中学数学】平行四辺形の性質の証明~定義と定理の違いを明確に~【中2数学】

図形問題の流れを一発で理解するmovie~全国入試問題解法 #shorts #数学 #math #高校入試

単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
図においてxの値を求めなさい.
興南高校過去問
この動画を見る
図においてxの値を求めなさい.
興南高校過去問
【得点源への道!】二次関数:京都府公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#1次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
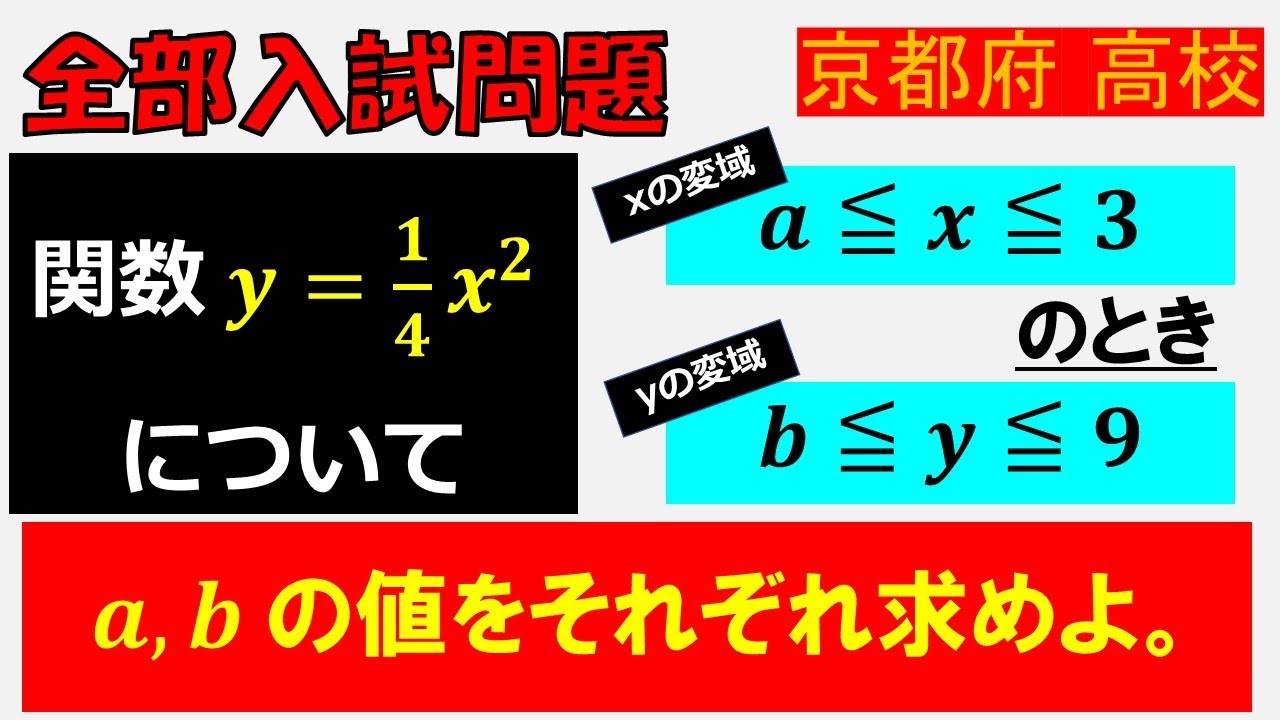
xの変域が$ a \leqq x \leqq 3$のとき,yの変域は$ b \leqq y \leqq 9 $である.
関数$ y=\dfrac{1}{4}x^2 $について$ a,b $の値をそれぞれ求めよ.
京都府高校過去問
この動画を見る
xの変域が$ a \leqq x \leqq 3$のとき,yの変域は$ b \leqq y \leqq 9 $である.
関数$ y=\dfrac{1}{4}x^2 $について$ a,b $の値をそれぞれ求めよ.
京都府高校過去問
勘で視力検査全問正解する確率

【公式より「思考」が大切!】整数:埼玉県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#数A#整数の性質#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
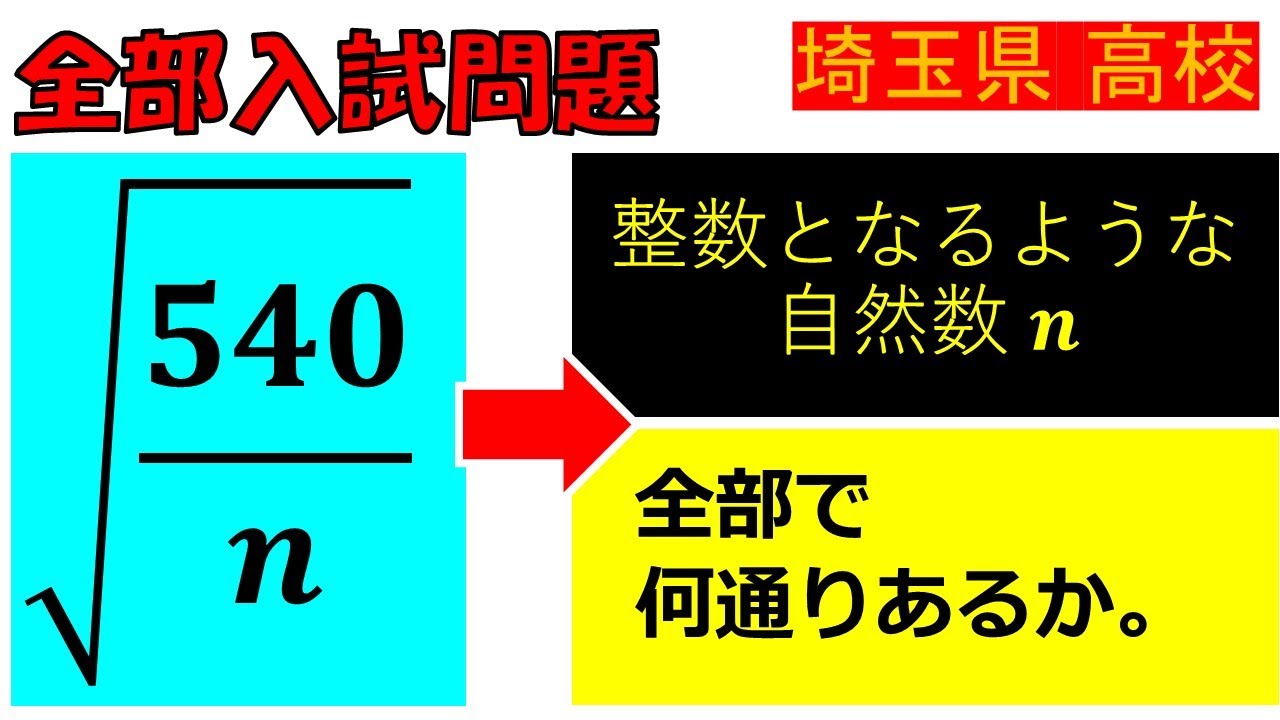
$ \sqrt{\dfrac{540}{n}}$
整数となるような自然数$ n $は全部で何通りあるか.
埼玉県高校過去問
この動画を見る
$ \sqrt{\dfrac{540}{n}}$
整数となるような自然数$ n $は全部で何通りあるか.
埼玉県高校過去問
【5つのパターン短時間でマスター!!】因数分解〔現役講師解説、中学、数学〕

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
3rd School
問題文全文(内容文):
①$x^2-9x+14$
②$x^2+x-12$
③$x^2-14x+49$
④$x^2-25$
⑤$x^2-6x$
この動画を見る
①$x^2-9x+14$
②$x^2+x-12$
③$x^2-14x+49$
④$x^2-25$
⑤$x^2-6x$
【1分で得意分野!】整数:精華女子高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
ある自然数を2乗して3引くところを間違えて2倍して3を引いたので
正しい答えより15小さくなった.ある自然数を求めよ.
精華女子高等学校過去問
この動画を見る
ある自然数を2乗して3引くところを間違えて2倍して3を引いたので
正しい答えより15小さくなった.ある自然数を求めよ.
精華女子高等学校過去問
中2数学「平行四辺形の面積の2等分線」【毎日配信】

単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
~例題~
次の図の四角形$OAB$は平行四辺形で,点$A$の座標は,(5,0),点$C$の座標は(1,4)です.
$y$軸上に$y$座標が4である点$P$をとるとき,点$P$を通り,四角形$OABC$の面積を2等分する直線の式を求めなさい.
この動画を見る
~例題~
次の図の四角形$OAB$は平行四辺形で,点$A$の座標は,(5,0),点$C$の座標は(1,4)です.
$y$軸上に$y$座標が4である点$P$をとるとき,点$P$を通り,四角形$OABC$の面積を2等分する直線の式を求めなさい.
小学生も解ける高校入試問題 大阪教育大附属

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
109×1009+91×991
大阪教育大学附属高等学校平野校舎
この動画を見る
109×1009+91×991
大阪教育大学附属高等学校平野校舎
丸暗記するな

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
数学を数楽に
問題文全文(内容文):
式の展開
$(a+b)^2 = a^2+2ab+b^2$
$(a-b)^2 = a^2-2ab+b^2$
この動画を見る
式の展開
$(a+b)^2 = a^2+2ab+b^2$
$(a-b)^2 = a^2-2ab+b^2$
連立方程式の難問を誰でも解けるようにする動画~全国入試問題解法 #shorts #数学 #高校入試 #裏ワザ

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{3x+4y}-\dfrac{4}{4x-3y}=10 \\
\dfrac{4}{3x+4y}+\dfrac{3}{4x-3y}=5
\end{array}
\right.
\end{eqnarray}$
を解け.
東大寺学園高校過去問
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{3x+4y}-\dfrac{4}{4x-3y}=10 \\
\dfrac{4}{3x+4y}+\dfrac{3}{4x-3y}=5
\end{array}
\right.
\end{eqnarray}$
を解け.
東大寺学園高校過去問
【題意から式を導く!】文章題:帝京高等学校~全国入試問題解法
単元:
#数学(中学生)#文章題#売買損益と食塩水#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
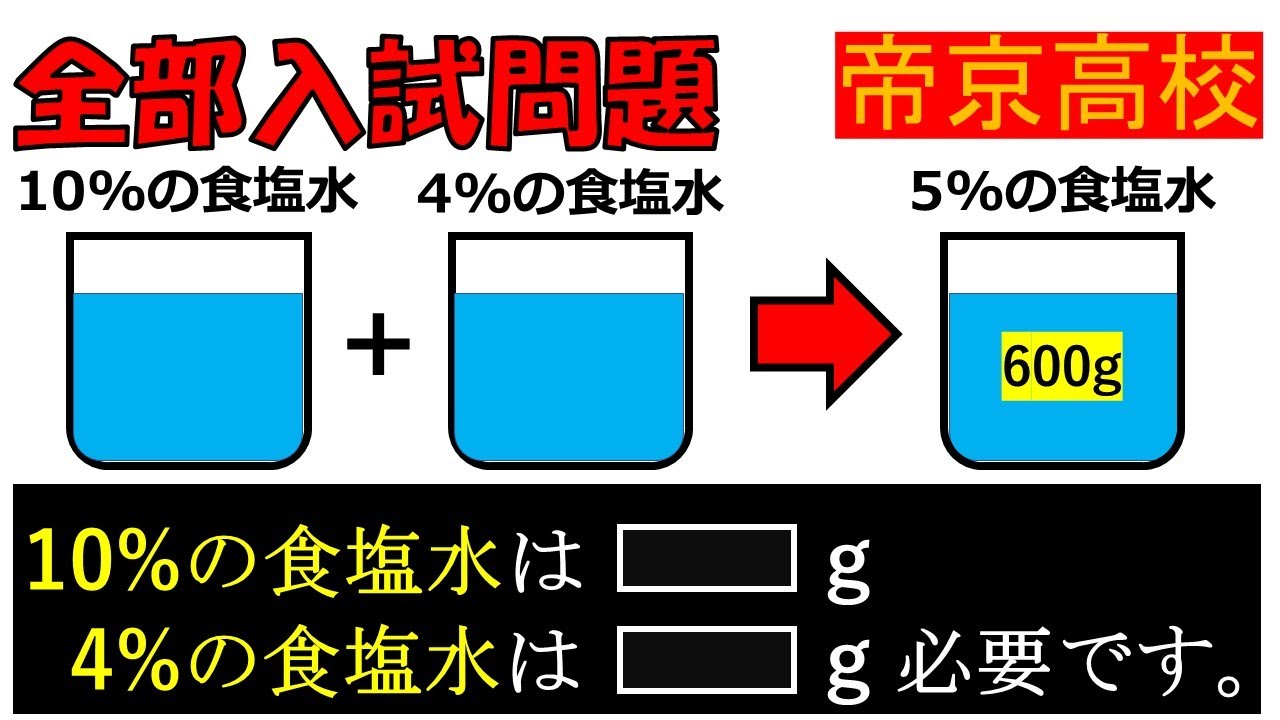
10%の食塩水と4%の食塩水を混ぜて5%の食塩水を600gつくるとき,
10%の食塩水と4%の食塩水はそれぞれ何g必要か?
帝京高等学校過去問
この動画を見る
10%の食塩水と4%の食塩水を混ぜて5%の食塩水を600gつくるとき,
10%の食塩水と4%の食塩水はそれぞれ何g必要か?
帝京高等学校過去問
【計算のルールと平方根のガイネン】平方根:東京都立新宿高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \dfrac{\sqrt{(-3)^2}+(-2)^2}{(-\sqrt2)^3}+\dfrac{(\sqrt3-2)^2}{\sqrt{2^3}}$を計算せよ.
都立新宿高校過去問
この動画を見る
$ \dfrac{\sqrt{(-3)^2}+(-2)^2}{(-\sqrt2)^3}+\dfrac{(\sqrt3-2)^2}{\sqrt{2^3}}$を計算せよ.
都立新宿高校過去問
【迷わず進め!】二次方程式:東京都立八王子東高等学校~全国入試問題解法

単元:
#数学(中学生)#数Ⅰ#数と式#2次関数#2次方程式と2次不等式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$ (x+1)^2+(x+1)(x+2)+4x+5=0 $を解け.
都立八王子東高校過去問
この動画を見る
2次方程式$ (x+1)^2+(x+1)(x+2)+4x+5=0 $を解け.
都立八王子東高校過去問
【奥が深い?スッキリ解答】一次関数:函館ラ・サール高等学校~全国入試問題解法

単元:
#数学(中学生)#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
1次関数$ y=ax+3(a \lt 0)$
xの変域$ -2 \leqq x \leqq 5$であるとき,yの変域$ -2 \leqq y \leqq b $となるような
aとbの値を求めなさい.
函館ラサール高校過去問
この動画を見る
1次関数$ y=ax+3(a \lt 0)$
xの変域$ -2 \leqq x \leqq 5$であるとき,yの変域$ -2 \leqq y \leqq b $となるような
aとbの値を求めなさい.
函館ラサール高校過去問
【よく見てみれば…!】因数分解:明治大学付属中野高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ (x^2+x)^2-x(x+1)-2 $を因数分解しなさい.
明大中野高校過去問
この動画を見る
$ (x^2+x)^2-x(x+1)-2 $を因数分解しなさい.
明大中野高校過去問
何の動画か分かる?
【「学ぶ」は「真似する」ところから】2元2次連立方程式⑤:中学からの連立方程式~全国入試問題解法
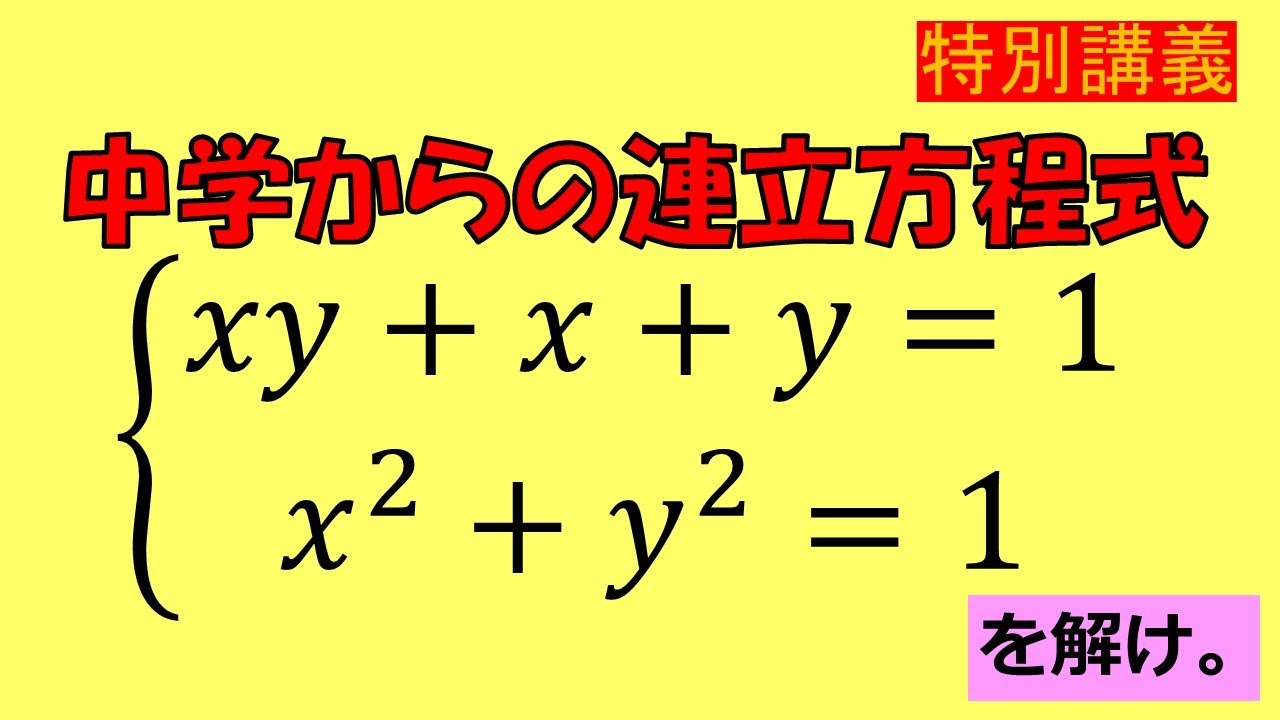
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
xy+x+y=1 \\
x^2+y^2=1
\end{array}
\right.
\end{eqnarray}$
を解け.
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
xy+x+y=1 \\
x^2+y^2=1
\end{array}
\right.
\end{eqnarray}$
を解け.
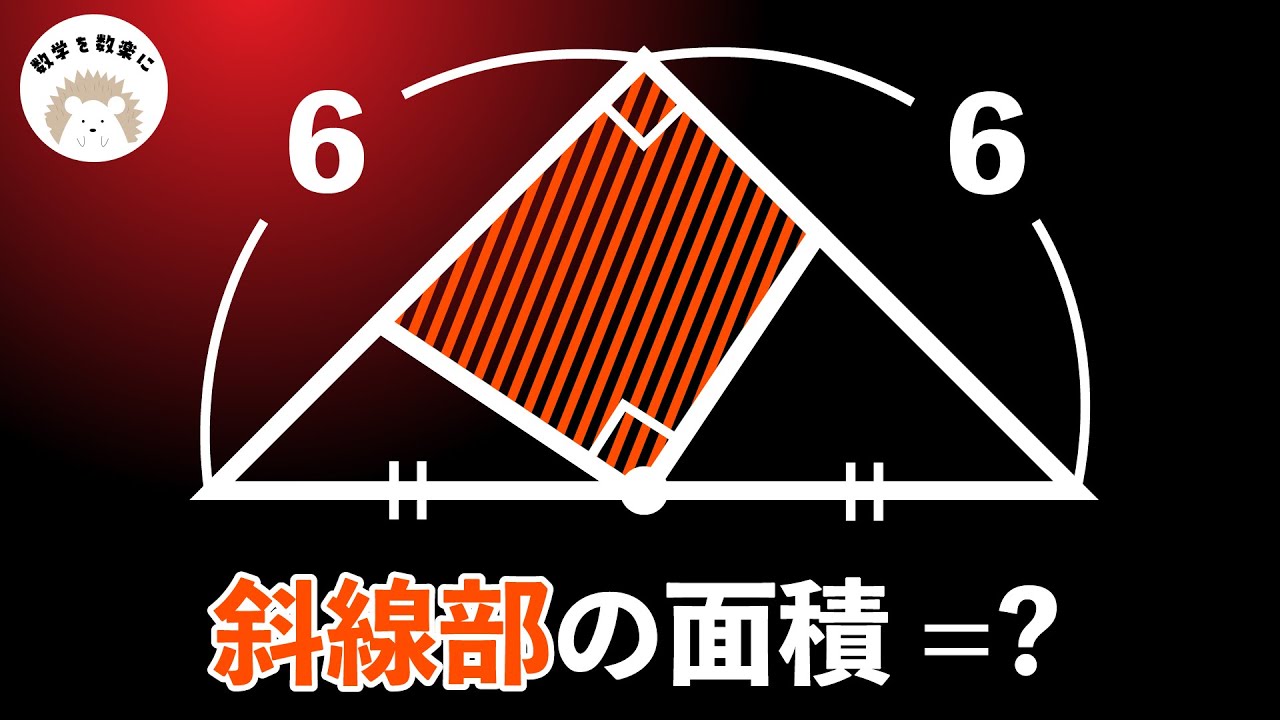
気付けば一瞬!! 直角二等辺三角形 小学生も解ける
【これまでの知識を利用して】2元2次連立方程式④:中学からの連立方程式~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x^2+xy-2y^2=4 \\
x^2+2xy-y^2=7
\end{array}
\right.
\end{eqnarray}$
を解け.
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x^2+xy-2y^2=4 \\
x^2+2xy-y^2=7
\end{array}
\right.
\end{eqnarray}$
を解け.
【やり方を短時間でマスター!!】連立方程式(代入法・加減法)〔現役講師解説、中学、数学〕

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
3rd School
問題文全文(内容文):
中学2年生 数学
連立方程式
加減法
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x + 2y = 15 \\
9x - 5y = 12
\end{array}
\right.
\end{eqnarray}$
代入法
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x - 2y = 2 \\
y = x + 2
\end{array}
\right.
\end{eqnarray}$
この動画を見る
中学2年生 数学
連立方程式
加減法
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x + 2y = 15 \\
9x - 5y = 12
\end{array}
\right.
\end{eqnarray}$
代入法
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x - 2y = 2 \\
y = x + 2
\end{array}
\right.
\end{eqnarray}$
二次関数と三角形には簡単に面積を導ける裏ワザがある~全国入試問題解法 #shorts #数学 #高校入試 #sound #裏ワザ

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
関数$ y=x^2 $のグラフ上に2点A,Bがある.
点A:x=-2,点B:x=1
(1)点Aのy座標を求めよ.
(2)直線ABの式を求めよ.
(3)$ \triangle OAB $の面積を求めよ.
長崎県高校過去問
この動画を見る
関数$ y=x^2 $のグラフ上に2点A,Bがある.
点A:x=-2,点B:x=1
(1)点Aのy座標を求めよ.
(2)直線ABの式を求めよ.
(3)$ \triangle OAB $の面積を求めよ.
長崎県高校過去問
中2数学「高さが等しい三角形の面積比②」

単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
~例題~
次の図の$\triangle ABC$で,点$D,E$は辺$AB$上の点で点$F,G$は辺$BC$上の点です.
線分$EF,DF,DG,AG$によって,$\triangle ABC$の面積が5等分されています.
(1)
$BG:GC$を最も簡単な整数の比で表しなさい.
(2)
$BC=15$cmのとき,$BF$の長さを求めなさい.
この動画を見る
~例題~
次の図の$\triangle ABC$で,点$D,E$は辺$AB$上の点で点$F,G$は辺$BC$上の点です.
線分$EF,DF,DG,AG$によって,$\triangle ABC$の面積が5等分されています.
(1)
$BG:GC$を最も簡単な整数の比で表しなさい.
(2)
$BC=15$cmのとき,$BF$の長さを求めなさい.
中2数学「高さが等しい三角形の面積比②」【毎日配信】

単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
~例題~
次の図の$\triangle ABC$で点$D,E$は辺$AB$上の点で点$F,G$は辺$BC$上の点です.
線分$EF,DF,DG,AG$によって$\triangle ABC$の面積が5等分されています.
(1)
$BG:GC$を最も簡単な整数の比で表しなさい.
(2)
$BC=15$cmのとき,$BF$の長さを求めなさい.
この動画を見る
~例題~
次の図の$\triangle ABC$で点$D,E$は辺$AB$上の点で点$F,G$は辺$BC$上の点です.
線分$EF,DF,DG,AG$によって$\triangle ABC$の面積が5等分されています.
(1)
$BG:GC$を最も簡単な整数の比で表しなさい.
(2)
$BC=15$cmのとき,$BF$の長さを求めなさい.
中2数学「高さが等しい三角形の面積比①」【毎日配信】

単元:
#数学(中学生)#中2数学#平行と合同#三角形と四角形
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~高さが等しい三角形の面積比①~
1 次の図の△ABCで、点は辺BC上の点で、BD=15cm, DC=10cmです。次の2つの三角形の面積の比を. 最も簡単な整数の比で表しなさい。
△ABCと△DEFの面積比は?
例2 次の図の△ABCで、点DはBC上の点で、BD:DC=3:5. 点は辺AC上の点で、AE:EC=2:1です。 また△ADEの面積は10cmです。
(1) △EDCの面積を求めなさい。
(2) △ABCの面積を求めなさい。
この動画を見る
中2~高さが等しい三角形の面積比①~
1 次の図の△ABCで、点は辺BC上の点で、BD=15cm, DC=10cmです。次の2つの三角形の面積の比を. 最も簡単な整数の比で表しなさい。
△ABCと△DEFの面積比は?
例2 次の図の△ABCで、点DはBC上の点で、BD:DC=3:5. 点は辺AC上の点で、AE:EC=2:1です。 また△ADEの面積は10cmです。
(1) △EDCの面積を求めなさい。
(2) △ABCの面積を求めなさい。
方程式立てずに解ける! 大阪教育大附属天王寺

単元:
#数学(中学生)#中1数学#文章題#文章題その他#平面図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
ある正方形の各辺の長さを1cmずつ短くすると面積が半分になった。
もとの正方形の一辺の長さは?
大阪教育大学附属高等学校天王寺校舎
この動画を見る
ある正方形の各辺の長さを1cmずつ短くすると面積が半分になった。
もとの正方形の一辺の長さは?
大阪教育大学附属高等学校天王寺校舎
