 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
補助線を引く喜びを
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
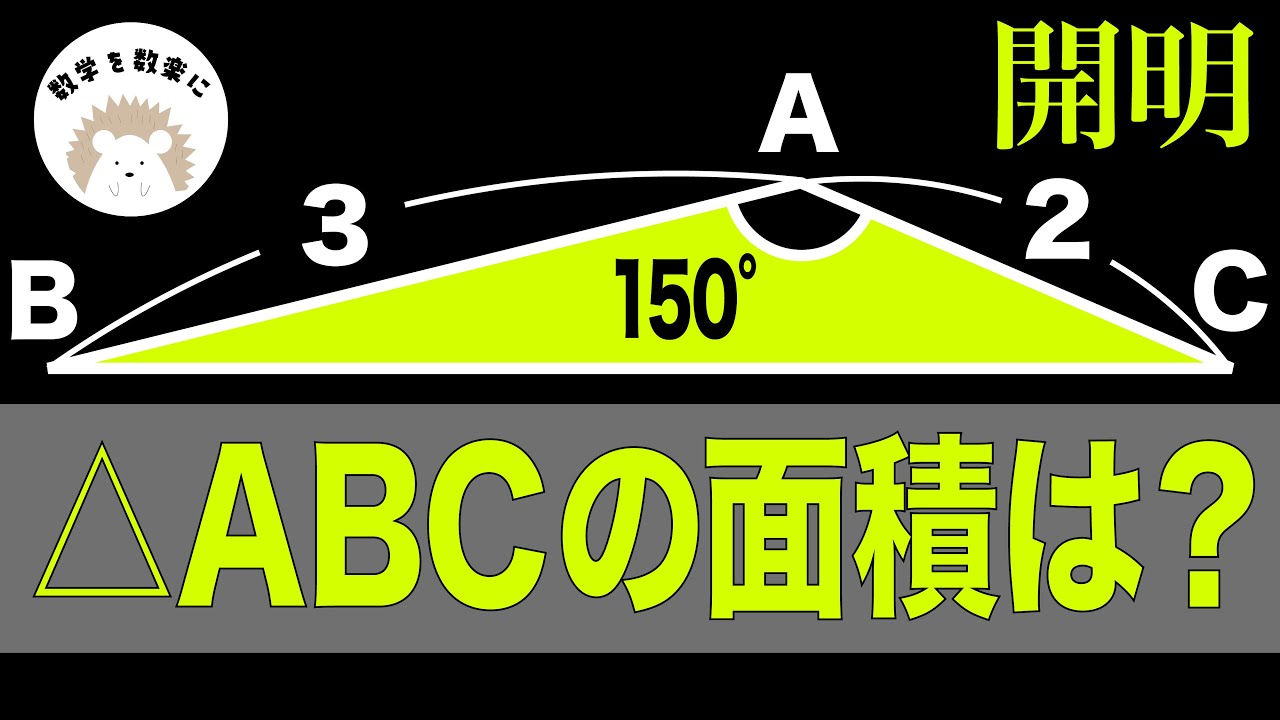
△ABC=?
*図は動画内参照
開明高等学校
この動画を見る
△ABC=?
*図は動画内参照
開明高等学校
√2✖️整数=整数??
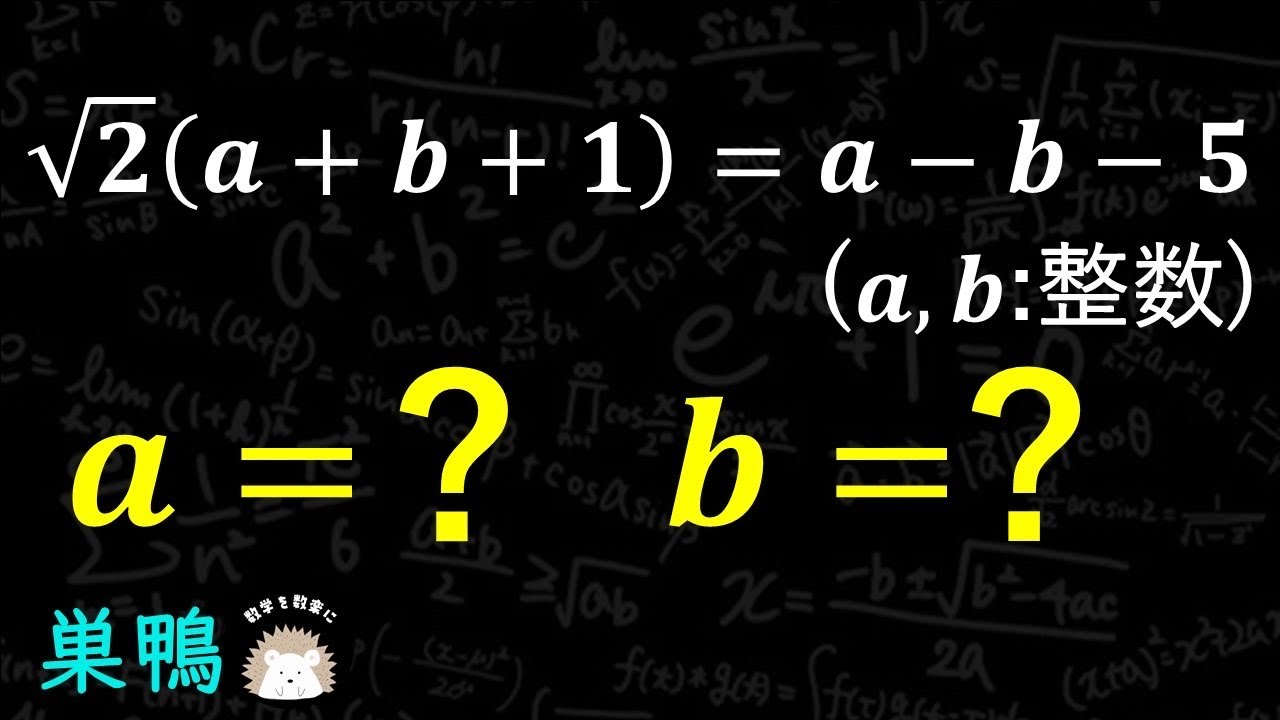
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt 2(a+b+1) = a-b-5$(a,bは整数)
a=? b=?
巣鴨高等学校
この動画を見る
$\sqrt 2(a+b+1) = a-b-5$(a,bは整数)
a=? b=?
巣鴨高等学校
【裏技】単位変換

単元:
#算数(中学受験)#計算と数の性質#数学(中学生)#単位・比と割合・比例・反比例#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
単位変換の説明動画です
この動画を見る
単位変換の説明動画です
これ説明して

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数学(中学生)#中1数学#中2数学#中3数学#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
2$\div \displaystyle \frac{1}{2}$
この動画を見る
2$\div \displaystyle \frac{1}{2}$
おうぎ形と円

単元:
#数学(中学生)#中3数学#数A#図形の性質#三平方の定理#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
赤い円の面積=?
*図は動画内参照
この動画を見る
赤い円の面積=?
*図は動画内参照
階乗に関する問題!!

単元:
#数学(中学生)#数列#数列とその和(等差・等比・階差・Σ)#高校入試過去問(数学)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$x! = \frac{(5!)!}{5!}$のときx=?
川端高校
この動画を見る
$x! = \frac{(5!)!}{5!}$のときx=?
川端高校
式の値 立命館 補足説明あり
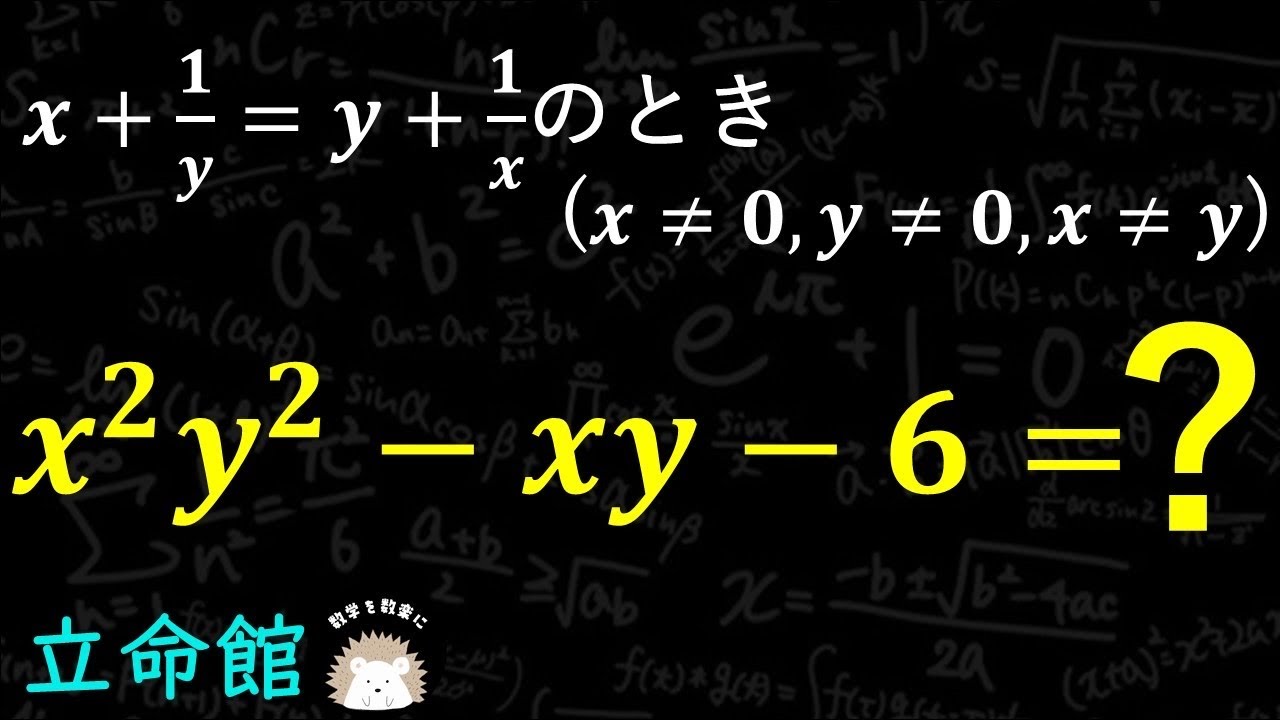
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x+\frac{1}{y} = y +\frac{1}{x}$のとき$(x \neq y)$
$x^2y^2 -xy -6 =?$
立命館高等学校
この動画を見る
$x+\frac{1}{y} = y +\frac{1}{x}$のとき$(x \neq y)$
$x^2y^2 -xy -6 =?$
立命館高等学校
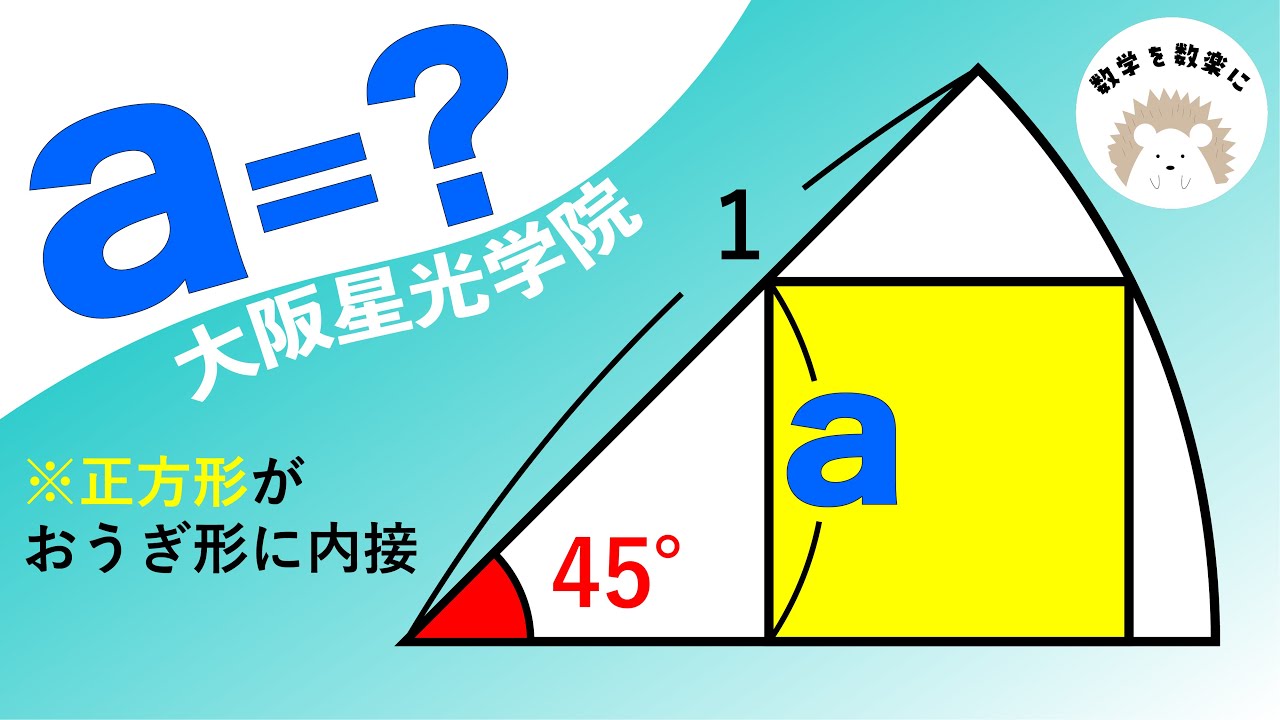
正方形がおうぎ形に内接 大阪星光学院
【ポイントは2つ!時間は有限!】整数:同志社高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 同志社高等学校
$a〇b=a-b$
$a*b=(a-1)(b-1)$
のように定めるとき
$\lbrace (2x-1) 〇(x+1)\rbrace$
$*\lbrace (3x-4y^2) 〇(3x-5y^2)\rbrace=15$
を満たす正の整数の組(x, y)をすべて求めよ。
この動画を見る
入試問題 同志社高等学校
$a〇b=a-b$
$a*b=(a-1)(b-1)$
のように定めるとき
$\lbrace (2x-1) 〇(x+1)\rbrace$
$*\lbrace (3x-4y^2) 〇(3x-5y^2)\rbrace=15$
を満たす正の整数の組(x, y)をすべて求めよ。
【裏技】ルートの近似値出し方

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
ルートの近似値出し方
この動画を見る
ルートの近似値出し方
分母が文字 昭和学院秀英

単元:
#数学(中学生)#数Ⅱ#式と証明#整式の除法・分数式・二項定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{3}{a} - \frac{2}{a+b} - \frac{3b}{a^2+ab}$
昭和学院秀英高等学校
この動画を見る
$\frac{3}{a} - \frac{2}{a+b} - \frac{3b}{a^2+ab}$
昭和学院秀英高等学校
放物線が回転!!!びびったら負け

単元:
#数学(中学生)#中2数学#中3数学#2次関数#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
放物線が原点を中心に30°回転
赤線部の面積=?
*図は動画内参照
早稲田大学 高等学院
この動画を見る
放物線が原点を中心に30°回転
赤線部の面積=?
*図は動画内参照
早稲田大学 高等学院
高校入試ではめずらしい整数問題

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$n^2+n$が100の倍数となる最も小さい自然数nは?
熊本マリスト学園高等学校
この動画を見る
$n^2+n$が100の倍数となる最も小さい自然数nは?
熊本マリスト学園高等学校
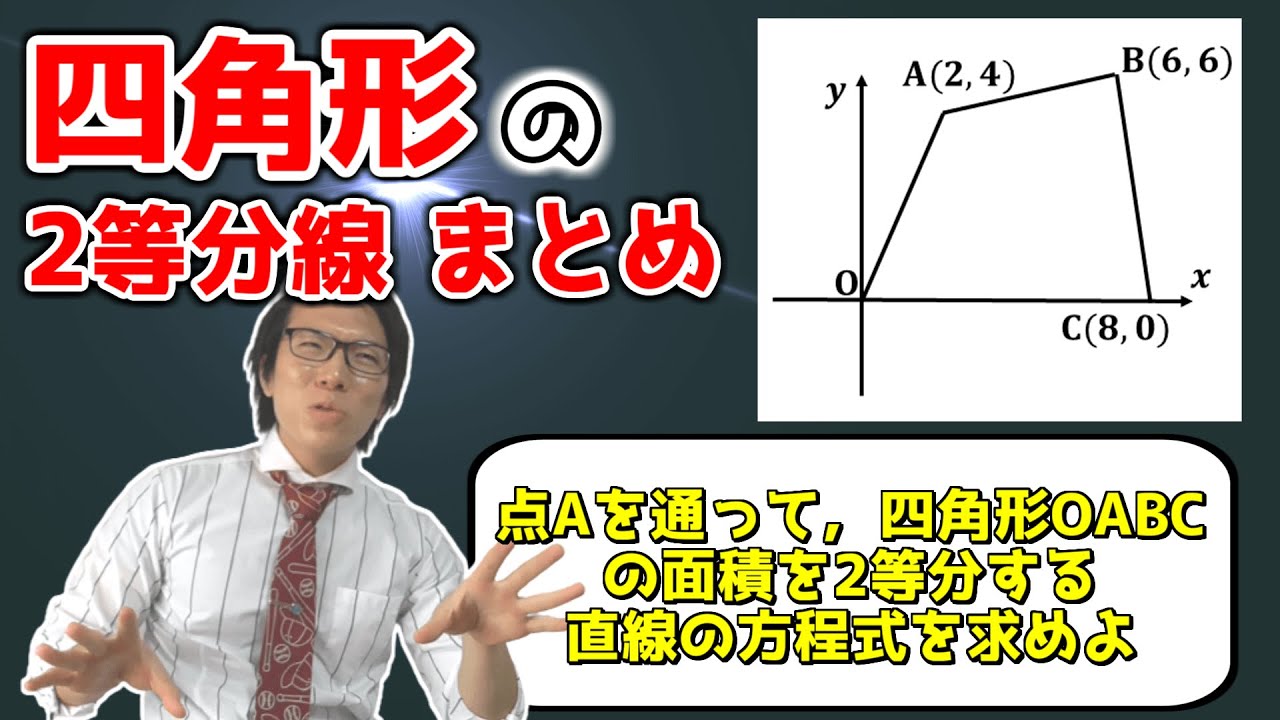
【中学数学】四角形の面積を2等分する直線のまとめ【中2数学】
単元:
#数学(中学生)#中1数学#中2数学#平行と合同#平面図形#三角形と四角形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
動画内の図、点Aを通て、四角形OABCを二等分する直線の式を求めよ。
この動画を見る
動画内の図、点Aを通て、四角形OABCを二等分する直線の式を求めよ。
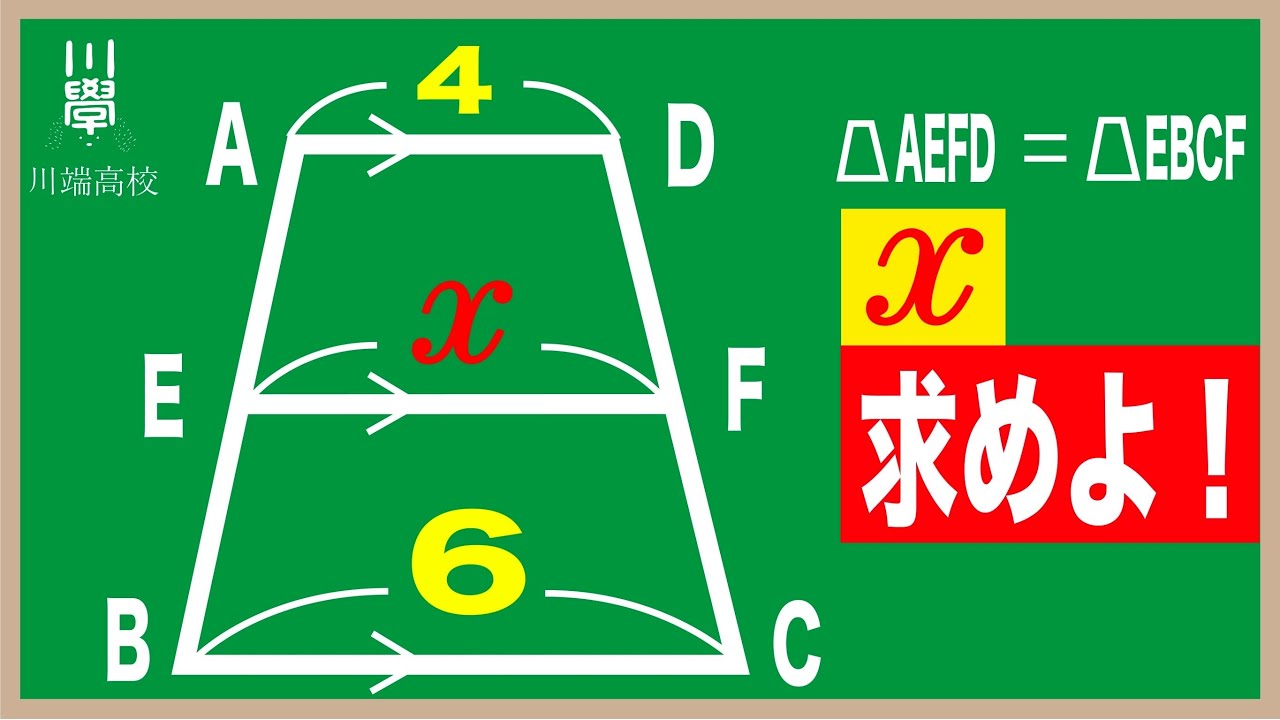
2つの台形の面積が等しいとき。(高校入試 数学)
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
台形AEFD=台形EBCFのとき x=?
*図は動画内参照
川端高校
この動画を見る
台形AEFD=台形EBCFのとき x=?
*図は動画内参照
川端高校
【一歩先行く3分間!】二次方程式:東大寺学園高等学校~全国入試問題解法

単元:
#数学(中学生)#2次方程式#高校入試過去問(数学)#数学
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東大寺学園高等学校
aの値とpの値を求めよ。
【$x$の二次方程式】
$\sqrt{ 5x^2 }+ax+4\sqrt{ 5 }=0$
の解の1つが
$\sqrt{ 15x }+ax+2\sqrt{ 3 }=0$
の解である。
もう一つの解を pとする。
この動画を見る
入試問題 東大寺学園高等学校
aの値とpの値を求めよ。
【$x$の二次方程式】
$\sqrt{ 5x^2 }+ax+4\sqrt{ 5 }=0$
の解の1つが
$\sqrt{ 15x }+ax+2\sqrt{ 3 }=0$
の解である。
もう一つの解を pとする。
【裏技】〇●の二等分線の図形の問題

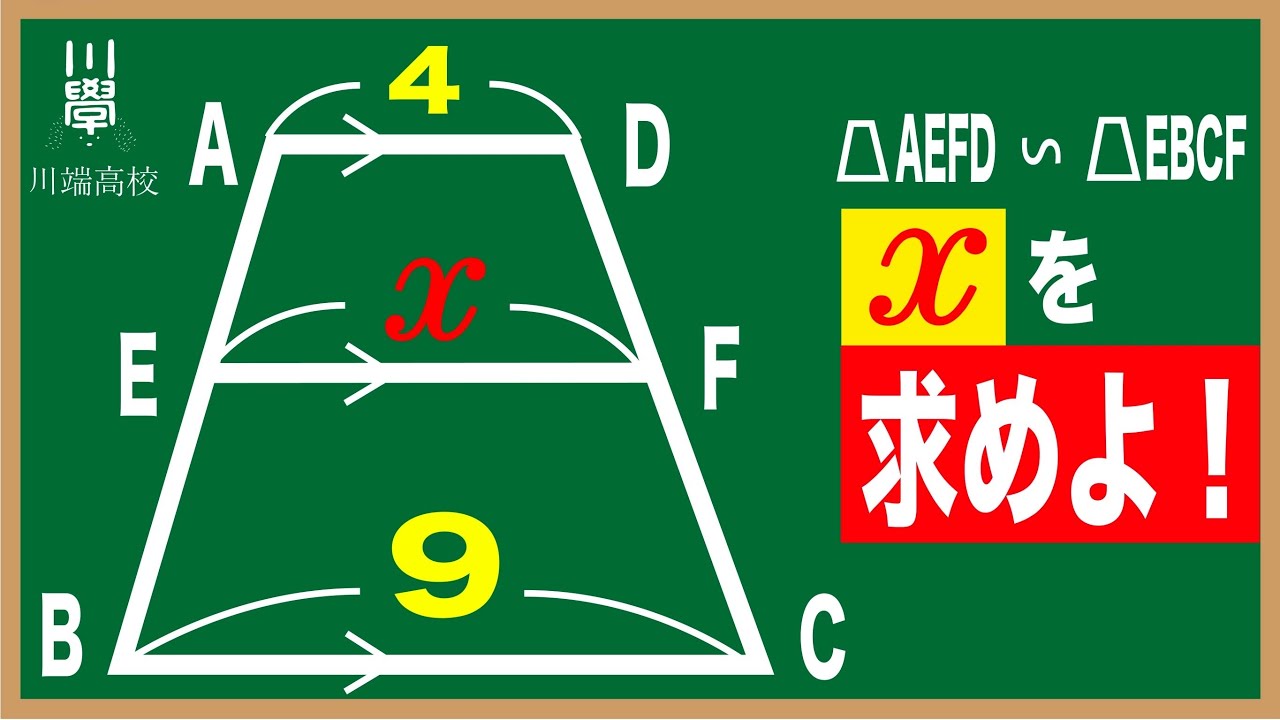
台形の相似 気づけば一瞬!!(高校入試 数学)
単元:
#数学(中学生)#中2数学#中3数学#相似な図形#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
台形AEFD∽台形EBCF
x=?
*図は動画内参照
川端高校
この動画を見る
台形AEFD∽台形EBCF
x=?
*図は動画内参照
川端高校
【高校受験対策/数学】関数55

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数55
Q.
図1のように、関数$y=-\frac{1}{4}x^2$・・・①のグラフ上に点$A(4,-4)$があり、$x$軸上に点$P$がある。
また、点$B(-2,-4)$がある。
問1
関数$y=-\frac{1}{4}x^2$について、$x$の変域が$-6 \leqq x \leqq 1$のとき、$y$の変域を求めなさい。
問2
$\triangle PAB$が二等辺三角形となる$P$はいくつあるか、求めなさい。
問3
図2のように、関数$y=ax^2(a \gt0)$・・・②のグラフ上に、 $x$座標が$-3$である点$D$がある。
$P$の$x$座標が$4$のとき、四角形$PABD$の面積が$50$となるような$a$の値を求めなさい。
この動画を見る
高校受験対策・関数55
Q.
図1のように、関数$y=-\frac{1}{4}x^2$・・・①のグラフ上に点$A(4,-4)$があり、$x$軸上に点$P$がある。
また、点$B(-2,-4)$がある。
問1
関数$y=-\frac{1}{4}x^2$について、$x$の変域が$-6 \leqq x \leqq 1$のとき、$y$の変域を求めなさい。
問2
$\triangle PAB$が二等辺三角形となる$P$はいくつあるか、求めなさい。
問3
図2のように、関数$y=ax^2(a \gt0)$・・・②のグラフ上に、 $x$座標が$-3$である点$D$がある。
$P$の$x$座標が$4$のとき、四角形$PABD$の面積が$50$となるような$a$の値を求めなさい。
【高校受験対策/数学】死守75

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#2次方程式#1次関数#平行と合同#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守75
①$-8+5$を計算しなさい。
②$1+3×-(\frac{2}{7})$を計算しなさい。
③$2(a+4b)+3(a-2b)$を計算しなさい。
④$\sqrt{27}-\frac{6}{\sqrt{3}}$を計算しなさい。
⑤$(x+1)^2+(x-4)(x+2)$を計算しなさい。
⑥次の式を因数分解しなさい。
$9x^2-4y^2$
⑦右の図のように、長方形$ABCD$を対角線$AC$を折り目として折り返し、
頂点$B$が移った点を$E$とする。
$\angle ACE=20°$のとき、$\angle x$の大きさを求めなさい。
⑧右の図のように、2点$A(2,6)$、$B(8,2)$がある。
次の文中の(ア)、(イ)にあてはまる数を求めなさい。
直線$y=ax$のグラフが、線分$AB$上の点を通るとき、$a$の値の範囲は、(ア) $ \leqq a\leqq$ (イ)である。
この動画を見る
高校受験対策・死守75
①$-8+5$を計算しなさい。
②$1+3×-(\frac{2}{7})$を計算しなさい。
③$2(a+4b)+3(a-2b)$を計算しなさい。
④$\sqrt{27}-\frac{6}{\sqrt{3}}$を計算しなさい。
⑤$(x+1)^2+(x-4)(x+2)$を計算しなさい。
⑥次の式を因数分解しなさい。
$9x^2-4y^2$
⑦右の図のように、長方形$ABCD$を対角線$AC$を折り目として折り返し、
頂点$B$が移った点を$E$とする。
$\angle ACE=20°$のとき、$\angle x$の大きさを求めなさい。
⑧右の図のように、2点$A(2,6)$、$B(8,2)$がある。
次の文中の(ア)、(イ)にあてはまる数を求めなさい。
直線$y=ax$のグラフが、線分$AB$上の点を通るとき、$a$の値の範囲は、(ア) $ \leqq a\leqq$ (イ)である。
問題というのは人間が作っている。だから、うまくできていることが多いのだ。

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
3x-5y=10のとき
$9x^2-25y^2-18x-70y-27$
徳島文理高等学校
この動画を見る
3x-5y=10のとき
$9x^2-25y^2-18x-70y-27$
徳島文理高等学校
【中学数学】連立方程式の演習~2014年石川県過去問~【高校受験】

ブーメラン型の面積を求める

僕は素数でありたい。 早稲田高等学院

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y = m \\
x-y = n
\end{array}
\right.
\end{eqnarray}
$
のとき素数x,y,m,nを求めよ。
早稲田大学高等学院
この動画を見る
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y = m \\
x-y = n
\end{array}
\right.
\end{eqnarray}
$
のとき素数x,y,m,nを求めよ。
早稲田大学高等学院
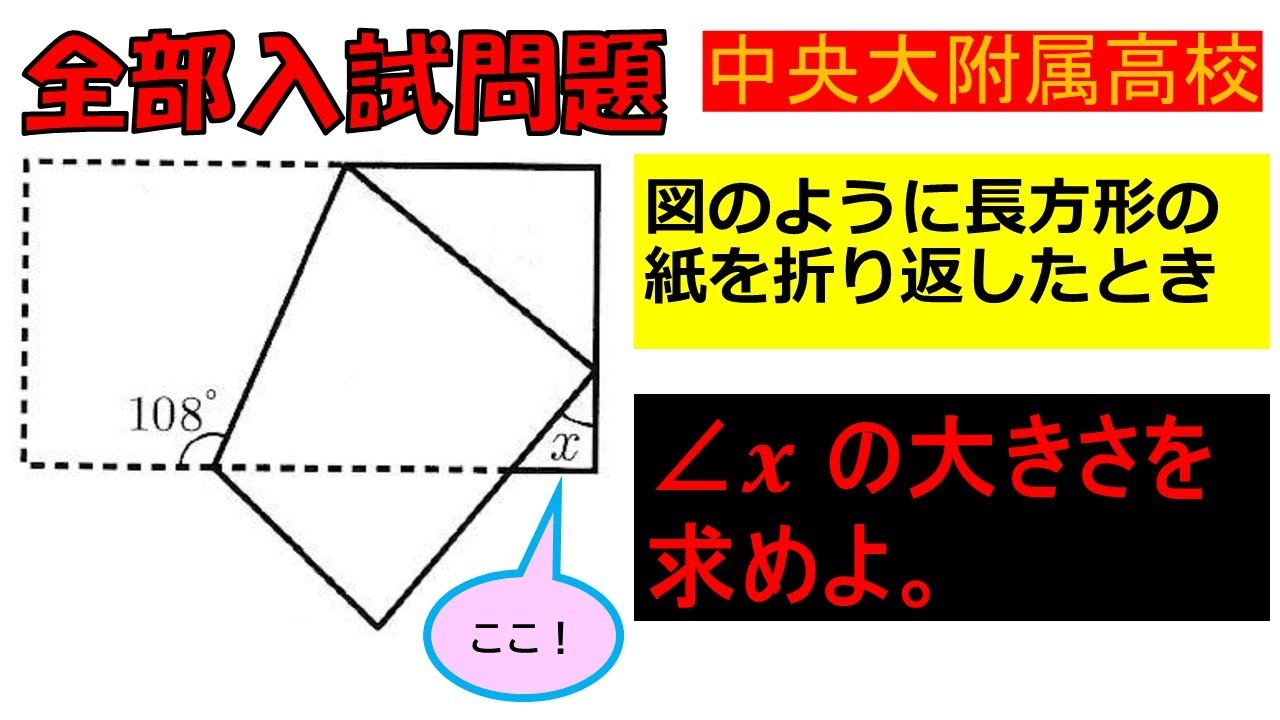
【意外と難しい⁈誰でも納得できる5分間!】図形:中央大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#図形の性質#高校入試過去問(数学)#数学
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 中央大学附属高等学校
図のように長方形の 紙を折り返したとき
$\angle x$の大きさを 求めよ。
※図は動画内参照
この動画を見る
入試問題 中央大学附属高等学校
図のように長方形の 紙を折り返したとき
$\angle x$の大きさを 求めよ。
※図は動画内参照
ルート16%

【中学数学】意外と間違える2次方程式の問題 3-5.5【中3数学】

早稲田高等学院 整数 数字がない!!

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y = m \\
xy = n \\
x>y\\
m,nは素数
\end{array}
\right.
\end{eqnarray}
$
自然数x,y,m,nを求めよ
早稲田大学高等学院
この動画を見る
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y = m \\
xy = n \\
x>y\\
m,nは素数
\end{array}
\right.
\end{eqnarray}
$
自然数x,y,m,nを求めよ
早稲田大学高等学院
図形の問題でこんなオチが待っているとは。。。
単元:
#算数(中学受験)#数学(中学生)#中1数学#平面図形#図形の移動#平面図形その他#平面図形
指導講師:
数学を数楽に
問題文全文(内容文):
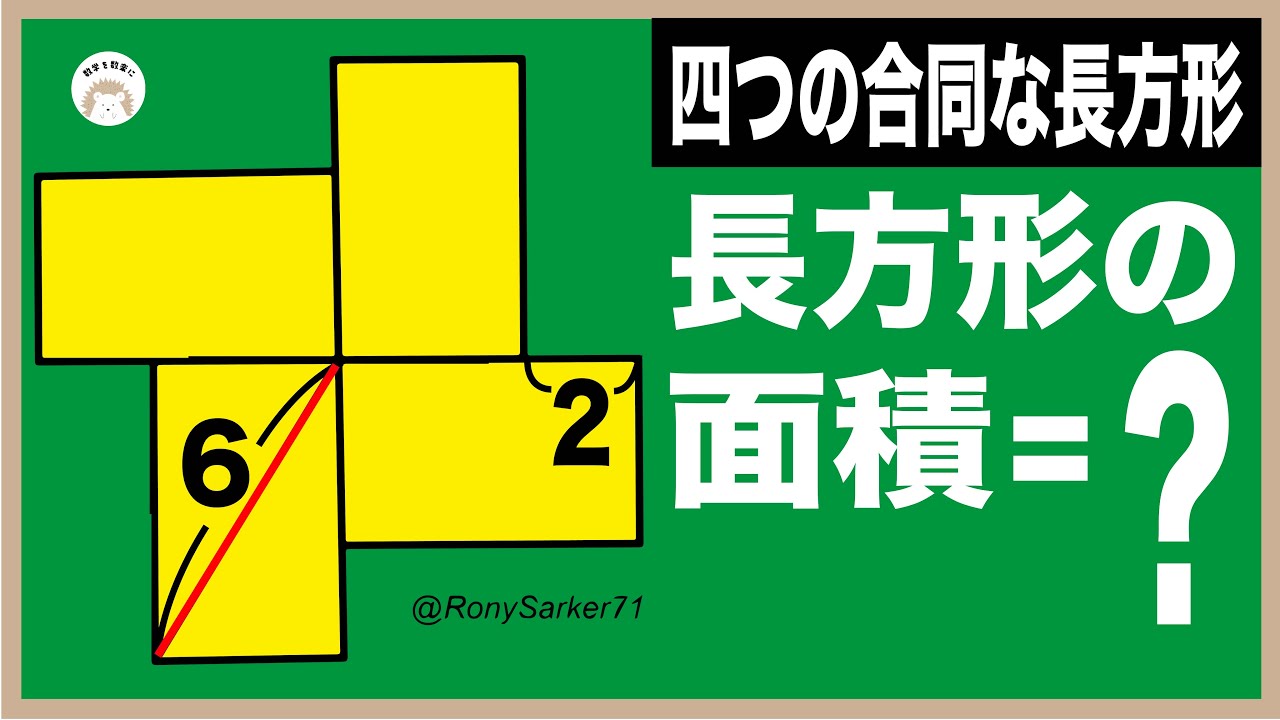
4つの合同な長方形
長方形の面積は?
*図は動画内参照
この動画を見る
4つの合同な長方形
長方形の面積は?
*図は動画内参照
【裏技】これすげぇ

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数学(中学生)#中1数学#中2数学#中3数学#約数・倍数を利用する問題#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
約分のテクニック紹介動画です
この動画を見る
約分のテクニック紹介動画です
