数学検定
数学検定
#数検準1級1次_4#不定積分
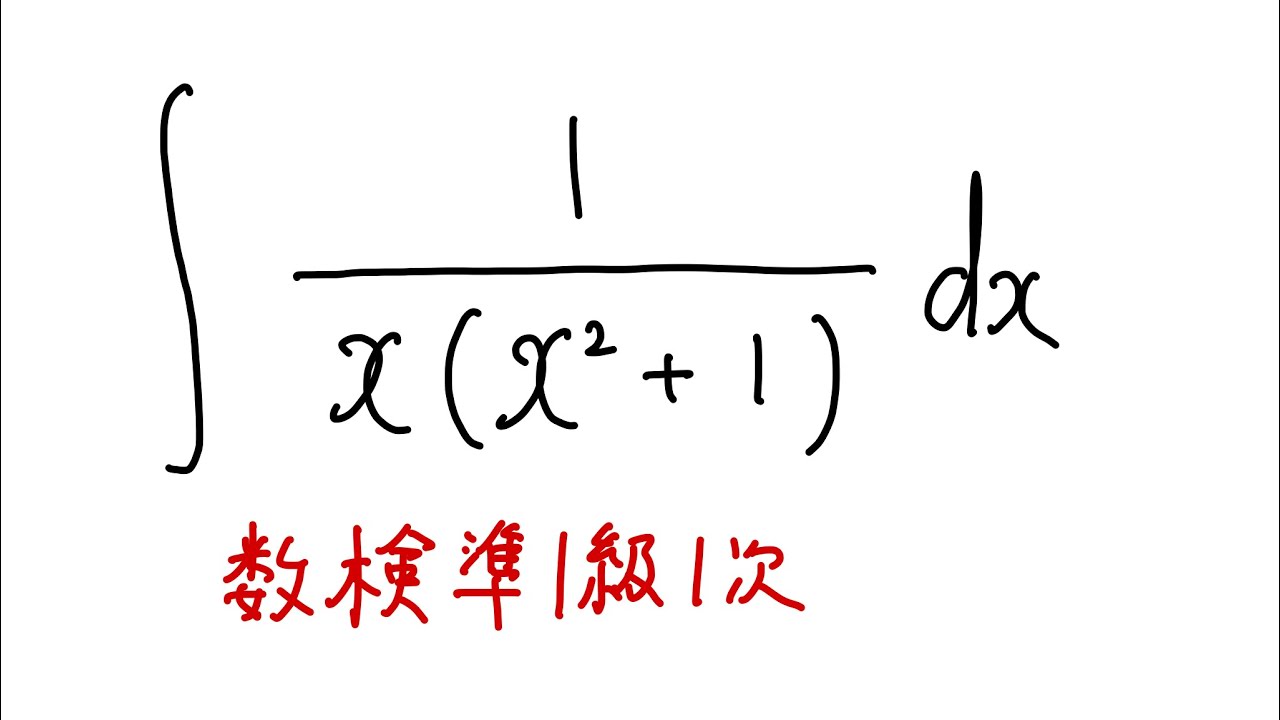
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{1}{x(x^2+1)} dx$
出典：数検準1級1次
この動画を見る
$\displaystyle \int \displaystyle \frac{1}{x(x^2+1)} dx$
出典：数検準1級1次
#数検準1級1次_2 #不定積分
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{e^x}{e^x+e^{-x}} dx$
出典：数検準1級1次
この動画を見る
$\displaystyle \int \displaystyle \frac{e^x}{e^x+e^{-x}} dx$
出典：数検準1級1次
#数検準1級1次 #7
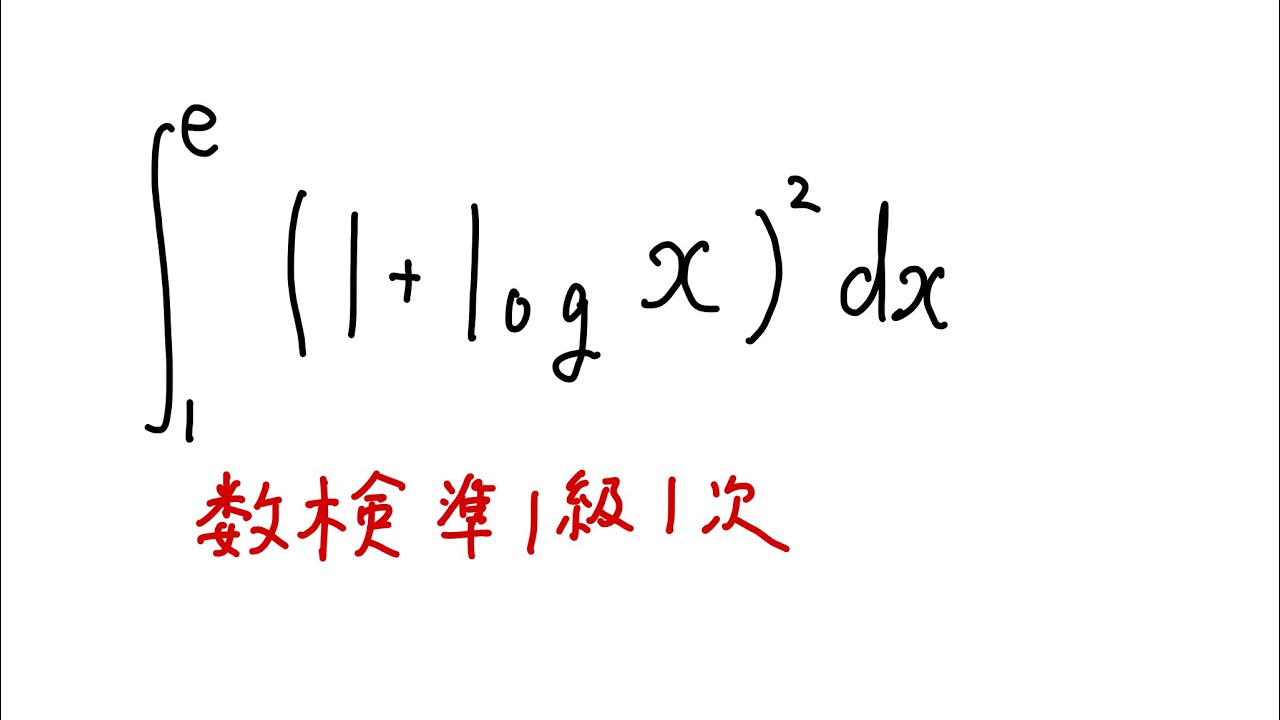
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{e} (1+log x)^2$ $dx$
出典：数検準1級1次
この動画を見る
$\displaystyle \int_{1}^{e} (1+log x)^2$ $dx$
出典：数検準1級1次
#数検準1級1次-1 #定積分
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
以下の定積分を解け。
$\displaystyle \int_{0}^{1} \displaystyle \frac{x}{x^4+2x^2+1} dx$
出典：数検準1級1次
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{1} \displaystyle \frac{x}{x^4+2x^2+1} dx$
出典：数検準1級1次
#数検準1級1次#6#極限
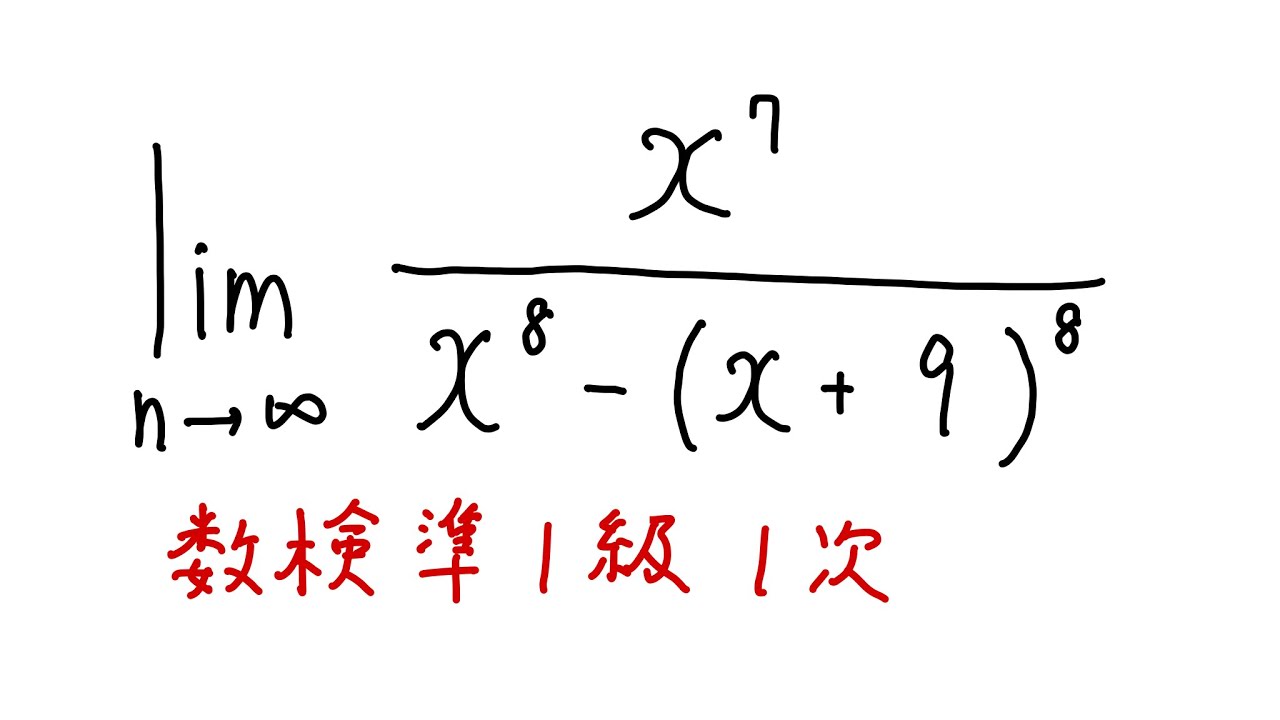
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x^7}{x^8-(x+9)^8}$
出典：数検準1級1次
この動画を見る
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x^7}{x^8-(x+9)^8}$
出典：数検準1級1次
#数検準1級1次過去問#極限#ますただ
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
以下の極限を解け。
$\displaystyle \lim_{ n \to \infty } \{2\sqrt{ n^2+4n }-\sqrt{ 4n^2+5n }\}$
出典：数検準1級1次
この動画を見る
以下の極限を解け。
$\displaystyle \lim_{ n \to \infty } \{2\sqrt{ n^2+4n }-\sqrt{ 4n^2+5n }\}$
出典：数検準1級1次
#数学検定準1級2次過去問#70「根性出すしかないんかなー」 #定積分
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} \displaystyle \frac{x^4(1-x)^4}{1+x^2} dx$
出典：数検準1級2次
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{x^4(1-x)^4}{1+x^2} dx$
出典：数検準1級2次
#数検準1級1次#5#不定積分
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ x+1 }} dx$
出典：数検準1級
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ x+1 }} dx$
出典：数検準1級
#数検準1級-1#定積分#ますただ
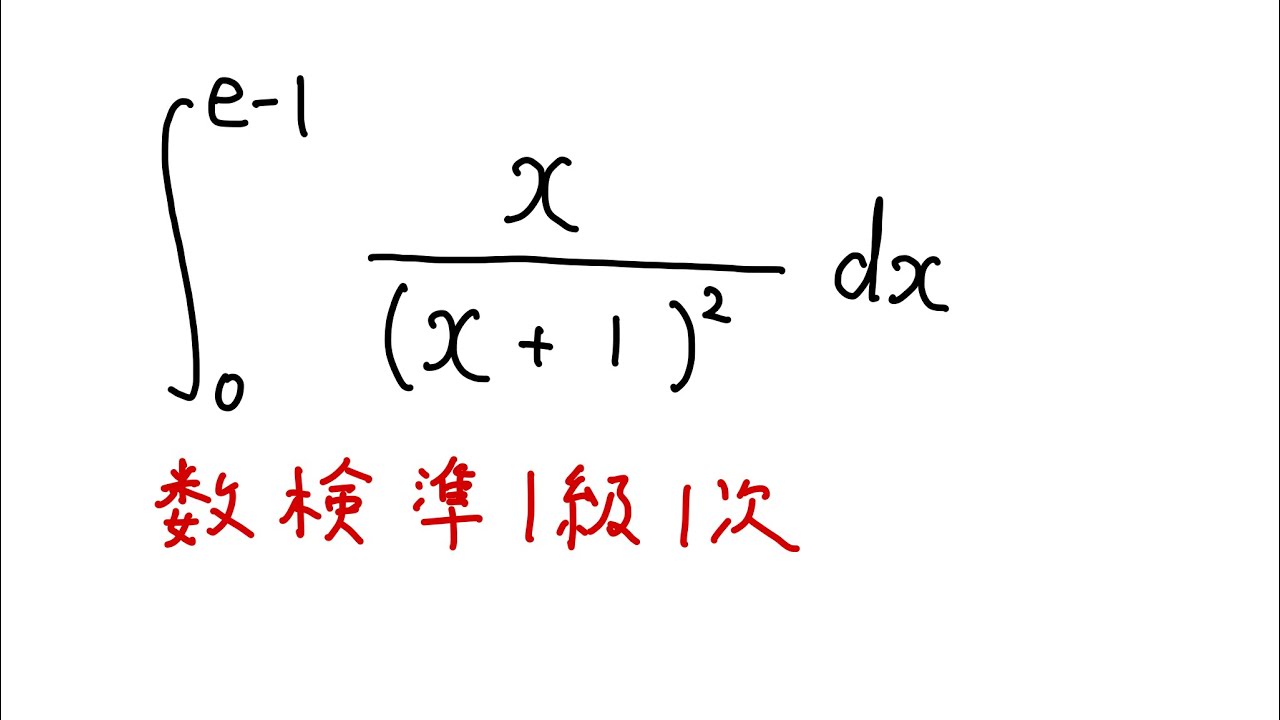
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{e-1} \displaystyle \frac{x}{(x+1)^2} dx$
出典：数検準1級1次
この動画を見る
$\displaystyle \int_{0}^{e-1} \displaystyle \frac{x}{(x+1)^2} dx$
出典：数検準1級1次
#数検準1級1次#極限#ますただ
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to 3 } \displaystyle \frac{x-3}{\sqrt{ 3x+7 }-4}$
出典：数検準1級1次
この動画を見る
$\displaystyle \lim_{ x \to 3 } \displaystyle \frac{x-3}{\sqrt{ 3x+7 }-4}$
出典：数検準1級1次
#数学検定準1級2次過去問#69「展開が最短かも」 #定積分
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} x^4(1-x)^4$ $dx$
出典：数検準1級1次
この動画を見る
$\displaystyle \int_{0}^{1} x^4(1-x)^4$ $dx$
出典：数検準1級1次
#数検準1級1次#定積分#ますただ
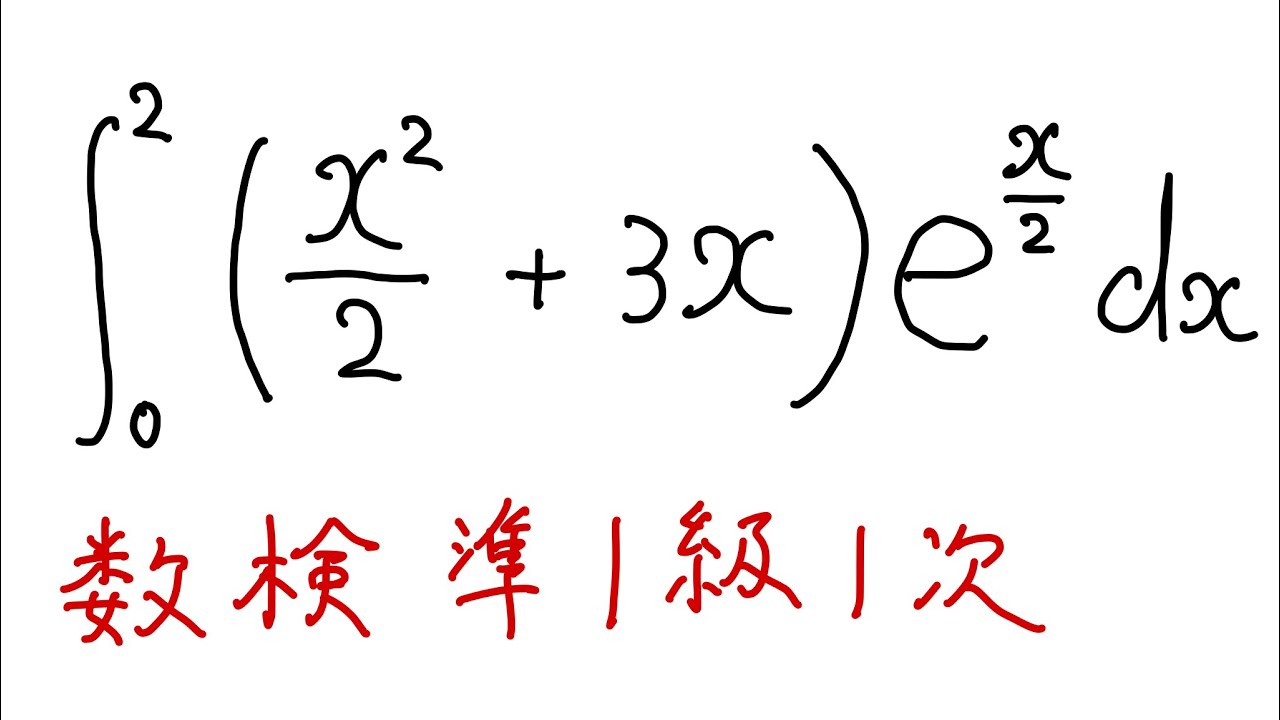
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{2} (\displaystyle \frac{x^2}{2}+3x)e^{\frac{x}{2}}dx$
出典：
この動画を見る
$\displaystyle \int_{0}^{2} (\displaystyle \frac{x^2}{2}+3x)e^{\frac{x}{2}}dx$
出典：
#数検準1級1次過去問#定積分
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{e^2-1} log(x+1)$ $dx$
出典：数検準1級1次
この動画を見る
$\displaystyle \int_{0}^{e^2-1} log(x+1)$ $dx$
出典：数検準1級1次
#68数学検定1級1次「答えはめっちゃスッキリ」 #定積分
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-1}^{ 1 } \displaystyle \frac{x^4+2x^3+4x^2+6x+2}{x^3+2x^2+2x+4}$ $dx$
出典：数検1級1次
この動画を見る
$\displaystyle \int_{-1}^{ 1 } \displaystyle \frac{x^4+2x^3+4x^2+6x+2}{x^3+2x^2+2x+4}$ $dx$
出典：数検1級1次
#67数学検定1級1次「こんな問題で時間使いたくない」 #因数分解
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$xy(x^2-y^2)+yz(y^2-z^2)+zx(z^2-x^2)$を因数分解せよ
出典：数検1級1次
この動画を見る
$xy(x^2-y^2)+yz(y^2-z^2)+zx(z^2-x^2)$を因数分解せよ
出典：数検1級1次
#66数学検定1級1次過去問「怖いのは計算ミスのみ」 #式変形
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$(1-\sqrt[ 3 ]{ 2 }+\sqrt[ 3 ]{ 4 })^3$を簡単にせよ
出典：数検1級1次
この動画を見る
$(1-\sqrt[ 3 ]{ 2 }+\sqrt[ 3 ]{ 4 })^3$を簡単にせよ
出典：数検1級1次
#64 #数検1級1次過去問 #高次方程式
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$4$次方程式
$x^4-4x-1=0$について、次の問いに答えよ。
１．上の方程式の実数解を求めよ。
２．上の方程式の虚数解を求めよ
出典：数検1級1次過去問
この動画を見る
$4$次方程式
$x^4-4x-1=0$について、次の問いに答えよ。
１．上の方程式の実数解を求めよ。
２．上の方程式の虚数解を求めよ
出典：数検1級1次過去問
高校数学：数学検定準1級2次：問題7 関数の増減と変曲点
単元：
#数学検定・数学甲子園・数学オリンピック等#微分とその応用#微分法#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$f(x)＝\displaystyle \frac{2x－1}{x^2－x＋1}$
について、次の問いに答えなさい。
(1) $f(x)$の増減を調べ、その極値を求めなさい。また、極値をとるときのxの値も求めなさい。
(2) $xy$平面における曲線$y＝f(x)$は３個の変曲点をもちます(このことを証明する必要はありません)。これらの変曲点の座標をすべて求めなさい。
この動画を見る
$f(x)＝\displaystyle \frac{2x－1}{x^2－x＋1}$
について、次の問いに答えなさい。
(1) $f(x)$の増減を調べ、その極値を求めなさい。また、極値をとるときのxの値も求めなさい。
(2) $xy$平面における曲線$y＝f(x)$は３個の変曲点をもちます(このことを証明する必要はありません)。これらの変曲点の座標をすべて求めなさい。
#64 #数検1級1次過去問「久しぶりに重積分やってみよー」 #重積分 #高専
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
領域$D$が次のように与えられている。
$D=\{(x,y)|0 \leq x \leq 1,0 \leq y \leq 1\}$
このとき、次の2重積分を計算せよ。
$\displaystyle \int\displaystyle \int_{D}|x-y|^{-\frac{2}{3}}dxdy$
出典：数検1級1次
この動画を見る
領域$D$が次のように与えられている。
$D=\{(x,y)|0 \leq x \leq 1,0 \leq y \leq 1\}$
このとき、次の2重積分を計算せよ。
$\displaystyle \int\displaystyle \int_{D}|x-y|^{-\frac{2}{3}}dxdy$
出典：数検1級1次
#60数検1級1次「ええ問題！落とし穴に注意」 数検1級1次
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
全ての実数$x$について
$\displaystyle \frac{\pi}{2} \lt \tan^{-1}x \lt \displaystyle \frac{\pi}{2}$とするとき、次の値を求めよ。
$\tan^{-1}1+\tan^{-1}2+\tan^{-1}3$
出典：数検1級1次
この動画を見る
全ての実数$x$について
$\displaystyle \frac{\pi}{2} \lt \tan^{-1}x \lt \displaystyle \frac{\pi}{2}$とするとき、次の値を求めよ。
$\tan^{-1}1+\tan^{-1}2+\tan^{-1}3$
出典：数検1級1次
高校数学：数学検定準1級2次：問題6 3次方程式の解と係数の関係
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#数学検定#数学検定準1級#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の２つの３次方程式
$x^3+10x^2+ax＋14＝0$
$x^3+2x^2+bx－2＝0$
はそれぞれ異なる３個の解をもちますが、そのうちの２個は共通な解です。このと き、定数$a,b$の値および共通な２個の解を求めなさい。
この動画を見る
次の２つの３次方程式
$x^3+10x^2+ax＋14＝0$
$x^3+2x^2+bx－2＝0$
はそれぞれ異なる３個の解をもちますが、そのうちの２個は共通な解です。このと き、定数$a,b$の値および共通な２個の解を求めなさい。
高校数学：数学検定準1級1次：問題6,7 双曲線の焦点、関数の極限
単元：
#数学検定・数学甲子園・数学オリンピック等#平面上の曲線#関数と極限#2次曲線#関数の極限#数学検定#数学検定準1級#数学(高校生)#数C#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
xy平面上の双曲線
$\frac{x^2}{36}-\frac{y^2}{64}=-1$
の焦点の座標を求めなさい。
次の極限値を求めなさい。
$\displaystyle \lim_{ x \to 1 }\displaystyle \frac{x^2+2x-3}{\sqrt[ 3 ]{ x }-1}$
この動画を見る
xy平面上の双曲線
$\frac{x^2}{36}-\frac{y^2}{64}=-1$
の焦点の座標を求めなさい。
次の極限値を求めなさい。
$\displaystyle \lim_{ x \to 1 }\displaystyle \frac{x^2+2x-3}{\sqrt[ 3 ]{ x }-1}$
高校数学：数学検定準1級1次:問題3,4 :ベクトルの内積、複素数平面絶対値と角度
単元：
#数学検定・数学甲子園・数学オリンピック等#平面上のベクトル#複素数平面#平面上のベクトルと内積#複素数平面#数学検定#数学検定準1級#数学(高校生)#数C
指導講師：
理数個別チャンネル
問題文全文(内容文)：
問題３ ３つの単位ベクトル$\vec{ a },\vec{ b },\vec{ c }$が2$\vec{ a }+3\vec{ b }+4\vec{ c }=\vec{ 0 }$を満たすとき、$\vec{ a }$と$\vec{ c }$の内積$\vec{ a }・\vec{ c }$を求めなさい。
ただし、$\vec{ 0 }$は零ベクトルを表します。
問題４ 複素数 $z＝－2－i$について、次の問いに答えなさい。ただし、iは虚数単位を表します。
① zの絶対値を求めなさい。
② zの偏角を$\theta$とします。このとき、$sin4\theta$の値を求めなさい。
この動画を見る
問題３ ３つの単位ベクトル$\vec{ a },\vec{ b },\vec{ c }$が2$\vec{ a }+3\vec{ b }+4\vec{ c }=\vec{ 0 }$を満たすとき、$\vec{ a }$と$\vec{ c }$の内積$\vec{ a }・\vec{ c }$を求めなさい。
ただし、$\vec{ 0 }$は零ベクトルを表します。
問題４ 複素数 $z＝－2－i$について、次の問いに答えなさい。ただし、iは虚数単位を表します。
① zの絶対値を求めなさい。
② zの偏角を$\theta$とします。このとき、$sin4\theta$の値を求めなさい。
#58数検1級1次「ぱっと見はちょろそうだけど・・・」 #方程式
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
方程式
$x^6-14x^4+17x^2-4=0$を解け。
出典：数検1級1次
この動画を見る
方程式
$x^6-14x^4+17x^2-4=0$を解け。
出典：数検1級1次
#57数検準1級1次「ほぼ1本道」 #極限
単元：
#数学検定・数学甲子園・数学オリンピック等#関数と極限#関数の極限#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to 1 } \displaystyle \frac{x^2+2x-3}{\sqrt[ 3 ]{ x }-1}$
出典：数検準1級1次
この動画を見る
$\displaystyle \lim_{ x \to 1 } \displaystyle \frac{x^2+2x-3}{\sqrt[ 3 ]{ x }-1}$
出典：数検準1級1次
#57数検準1級1次 #定積分
単元：
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{2} (\displaystyle \frac{x^2}{2}+3x)e^{\frac{x}{2}}\ dx$
出典：数検準1級1次
この動画を見る
$\displaystyle \int_{0}^{2} (\displaystyle \frac{x^2}{2}+3x)e^{\frac{x}{2}}\ dx$
出典：数検準1級1次
#56数検１級１次 過去問 #4次方程式
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
方程式
$x^4-4x-1=0$の実数解を求めよ
出典：数検1級1次
この動画を見る
方程式
$x^4-4x-1=0$の実数解を求めよ
出典：数検1級1次
【数検準2級】高校数学：数学検定準2級2次：問7
単元：
#数学検定・数学甲子園・数学オリンピック等#その他#数学検定#数学検定準2級#その他#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
問7. 次の問いに答えなさい。
(10) さきこさんとゆうたさんは、次のような数当てゲームをしています。
① さきこさんは、４桁の数を決めて紙に書く。ただし、どの位の数字も異なり、０は含まないものとする。
② ゆうたさんは、さきこさんが書いた４桁の数を予想して伝える。
③ さきこさんは、ゆうたさんが予想した４桁の数で、位と数字も当たっている数字の個数と、位は違うが数字が当たっている数字の
個数をヒントとして伝える。
④ ゆうたさんは、さきこさんのヒントをもとに、再び数を予想する。
ゆうたさんは６回めの予想で、さきこさんが書いた４桁の数を当てました。下の表は、ゆうたさんが５回めまでに予想した数を、それに対するさきこ
さんのヒントです。
このとき、さきこさんが書いた４桁の数を求めなさい。この問題は答えだけを書いてください。
この動画を見る
問7. 次の問いに答えなさい。
(10) さきこさんとゆうたさんは、次のような数当てゲームをしています。
① さきこさんは、４桁の数を決めて紙に書く。ただし、どの位の数字も異なり、０は含まないものとする。
② ゆうたさんは、さきこさんが書いた４桁の数を予想して伝える。
③ さきこさんは、ゆうたさんが予想した４桁の数で、位と数字も当たっている数字の個数と、位は違うが数字が当たっている数字の
個数をヒントとして伝える。
④ ゆうたさんは、さきこさんのヒントをもとに、再び数を予想する。
ゆうたさんは６回めの予想で、さきこさんが書いた４桁の数を当てました。下の表は、ゆうたさんが５回めまでに予想した数を、それに対するさきこ
さんのヒントです。
このとき、さきこさんが書いた４桁の数を求めなさい。この問題は答えだけを書いてください。
【数検準2級】高校数学：数学検定準2級2次：問6
単元：
#数A#数学検定・数学甲子園・数学オリンピック等#場合の数と確率#確率#数学検定#数学検定準2級#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
問6. AチームとBチームが野球の試合を行います。どの試合も、AチームがBチームに勝つ確率は1/3で、引き分けはないものとします。
これについて、次の問いに答えなさい。
(8) ３試合めまで終えた時点でAチームが３勝０敗となる確率を求めなさい。この問題は答えだけを書いてください。
(9) ５試合めまで終えた時点でAチームが３勝２敗となる確率を求めなさい。
この動画を見る
問6. AチームとBチームが野球の試合を行います。どの試合も、AチームがBチームに勝つ確率は1/3で、引き分けはないものとします。
これについて、次の問いに答えなさい。
(8) ３試合めまで終えた時点でAチームが３勝０敗となる確率を求めなさい。この問題は答えだけを書いてください。
(9) ５試合めまで終えた時点でAチームが３勝２敗となる確率を求めなさい。
【数検準2級】高校数学：数学検定準2級2次：問5
単元：
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#図形と計量#三角比（三角比・拡張・相互関係・単位円）#三角比への応用（正弦・余弦・面積）#数学検定#数学検定準2級#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
問5. 次の問いに答えなさい。
(7) 地点Aから、湖を隔てた地点Bまでの距離を測定するために、地点Aから100ｍ、地点Ｂから60ｍ離れたところに地点Ｐをとります。地点Ｐから地点Ａ、Ｂをみて$\angle ＡＰＢ$の大きさを調べたところ、$\angle ＡＰＢ＝120°$でした。
このとき、2地点Ａ、Ｂ間の距離は何ｍですか。余弦定理を用いて求めなさい。
この動画を見る
問5. 次の問いに答えなさい。
(7) 地点Aから、湖を隔てた地点Bまでの距離を測定するために、地点Aから100ｍ、地点Ｂから60ｍ離れたところに地点Ｐをとります。地点Ｐから地点Ａ、Ｂをみて$\angle ＡＰＢ$の大きさを調べたところ、$\angle ＡＰＢ＝120°$でした。
このとき、2地点Ａ、Ｂ間の距離は何ｍですか。余弦定理を用いて求めなさい。