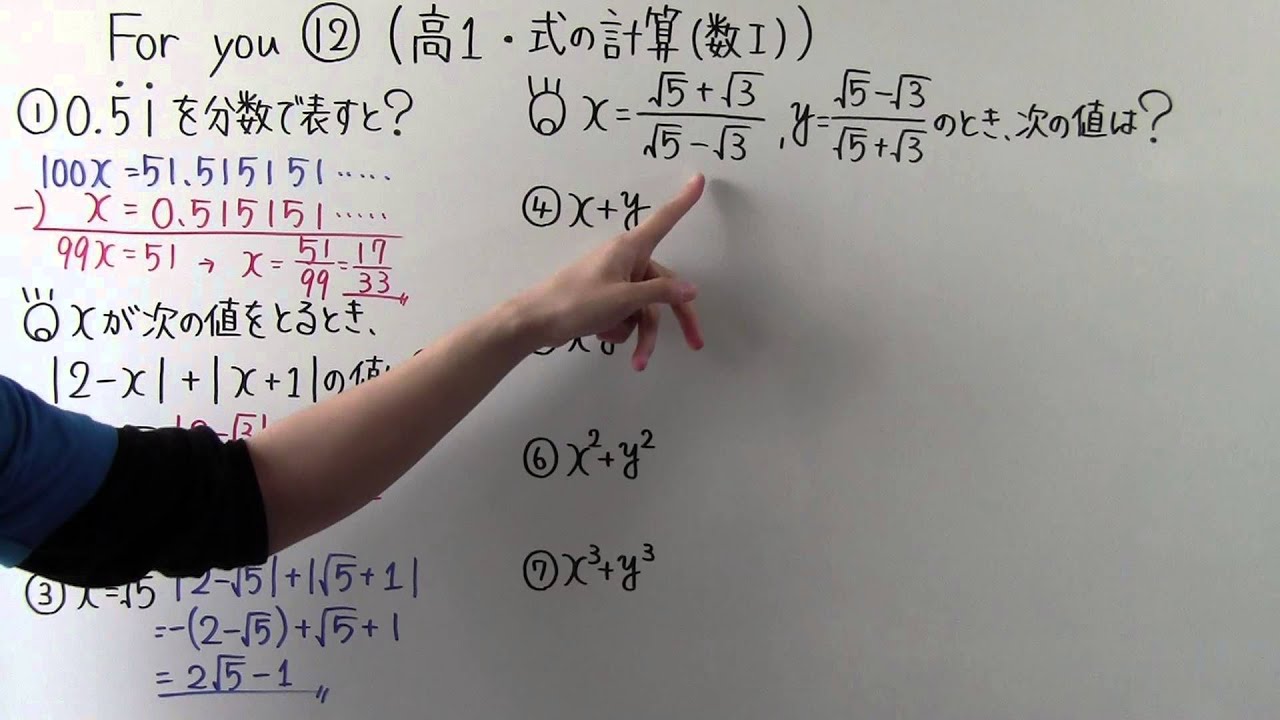問題文全文(内容文):
${\Large\boxed{1}}$ 座標平面上の原点を中心とする$半径2$の円を$C_1$、中心の座標が$(7,0)$、$半径3$の円を$C_2$とする。さらに$r$を正の実数とするとき、$C_1$と$C_2$に同時に外接する円で、その中心の座標が$(a,b)$、半径が$r$であるものを$C_3$とする。ただし、2つの円が外接するとは、それらが$1点$を共有し、中心が互いの外部にあるときをいう。
$(1)r$の最小値は$\boxed{\ \ ア\ \ }$であり、$a$の最大値は$\boxed{\ \ イ\ \ }$となる。
$(2)a$と$b$は関係式$b^2=\boxed{\ \ ウエ\ \ }(a+\boxed{\ \ オカ\ \ })(a-4)$を満たす。
$(3)C_3$が$直線x=-3$に接するとき、$a=\frac{\boxed{\ \ キク\ \ }}{\boxed{\ \ ケ\ \ }},$ $|b|=\frac{\sqrt{\boxed{\ \ コサシ\ \ }}}{\boxed{\ \ ス\ \ }}$である。
$(4)点(a,b)$と原点を通る直線と、$点(a,b)$と$点(7,0)$を通る直線が直交するとき、
$|b|=\frac{\boxed{\ \ セソ\ \ }}{\boxed{\ \ タ\ \ }}$となる。
2021慶應義塾大学経済学部過去問
${\Large\boxed{1}}$ 座標平面上の原点を中心とする$半径2$の円を$C_1$、中心の座標が$(7,0)$、$半径3$の円を$C_2$とする。さらに$r$を正の実数とするとき、$C_1$と$C_2$に同時に外接する円で、その中心の座標が$(a,b)$、半径が$r$であるものを$C_3$とする。ただし、2つの円が外接するとは、それらが$1点$を共有し、中心が互いの外部にあるときをいう。
$(1)r$の最小値は$\boxed{\ \ ア\ \ }$であり、$a$の最大値は$\boxed{\ \ イ\ \ }$となる。
$(2)a$と$b$は関係式$b^2=\boxed{\ \ ウエ\ \ }(a+\boxed{\ \ オカ\ \ })(a-4)$を満たす。
$(3)C_3$が$直線x=-3$に接するとき、$a=\frac{\boxed{\ \ キク\ \ }}{\boxed{\ \ ケ\ \ }},$ $|b|=\frac{\sqrt{\boxed{\ \ コサシ\ \ }}}{\boxed{\ \ ス\ \ }}$である。
$(4)点(a,b)$と原点を通る直線と、$点(a,b)$と$点(7,0)$を通る直線が直交するとき、
$|b|=\frac{\boxed{\ \ セソ\ \ }}{\boxed{\ \ タ\ \ }}$となる。
2021慶應義塾大学経済学部過去問
単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 座標平面上の原点を中心とする$半径2$の円を$C_1$、中心の座標が$(7,0)$、$半径3$の円を$C_2$とする。さらに$r$を正の実数とするとき、$C_1$と$C_2$に同時に外接する円で、その中心の座標が$(a,b)$、半径が$r$であるものを$C_3$とする。ただし、2つの円が外接するとは、それらが$1点$を共有し、中心が互いの外部にあるときをいう。
$(1)r$の最小値は$\boxed{\ \ ア\ \ }$であり、$a$の最大値は$\boxed{\ \ イ\ \ }$となる。
$(2)a$と$b$は関係式$b^2=\boxed{\ \ ウエ\ \ }(a+\boxed{\ \ オカ\ \ })(a-4)$を満たす。
$(3)C_3$が$直線x=-3$に接するとき、$a=\frac{\boxed{\ \ キク\ \ }}{\boxed{\ \ ケ\ \ }},$ $|b|=\frac{\sqrt{\boxed{\ \ コサシ\ \ }}}{\boxed{\ \ ス\ \ }}$である。
$(4)点(a,b)$と原点を通る直線と、$点(a,b)$と$点(7,0)$を通る直線が直交するとき、
$|b|=\frac{\boxed{\ \ セソ\ \ }}{\boxed{\ \ タ\ \ }}$となる。
2021慶應義塾大学経済学部過去問
${\Large\boxed{1}}$ 座標平面上の原点を中心とする$半径2$の円を$C_1$、中心の座標が$(7,0)$、$半径3$の円を$C_2$とする。さらに$r$を正の実数とするとき、$C_1$と$C_2$に同時に外接する円で、その中心の座標が$(a,b)$、半径が$r$であるものを$C_3$とする。ただし、2つの円が外接するとは、それらが$1点$を共有し、中心が互いの外部にあるときをいう。
$(1)r$の最小値は$\boxed{\ \ ア\ \ }$であり、$a$の最大値は$\boxed{\ \ イ\ \ }$となる。
$(2)a$と$b$は関係式$b^2=\boxed{\ \ ウエ\ \ }(a+\boxed{\ \ オカ\ \ })(a-4)$を満たす。
$(3)C_3$が$直線x=-3$に接するとき、$a=\frac{\boxed{\ \ キク\ \ }}{\boxed{\ \ ケ\ \ }},$ $|b|=\frac{\sqrt{\boxed{\ \ コサシ\ \ }}}{\boxed{\ \ ス\ \ }}$である。
$(4)点(a,b)$と原点を通る直線と、$点(a,b)$と$点(7,0)$を通る直線が直交するとき、
$|b|=\frac{\boxed{\ \ セソ\ \ }}{\boxed{\ \ タ\ \ }}$となる。
2021慶應義塾大学経済学部過去問
投稿日:2021.07.05