【数学】中3-34 二次関数の式をもとめよう - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(中学生) > 中３数学 > 2次関数 > 【数学】中3-34 二次関数の式をもとめよう

【数学】中3-34 二次関数の式をもとめよう

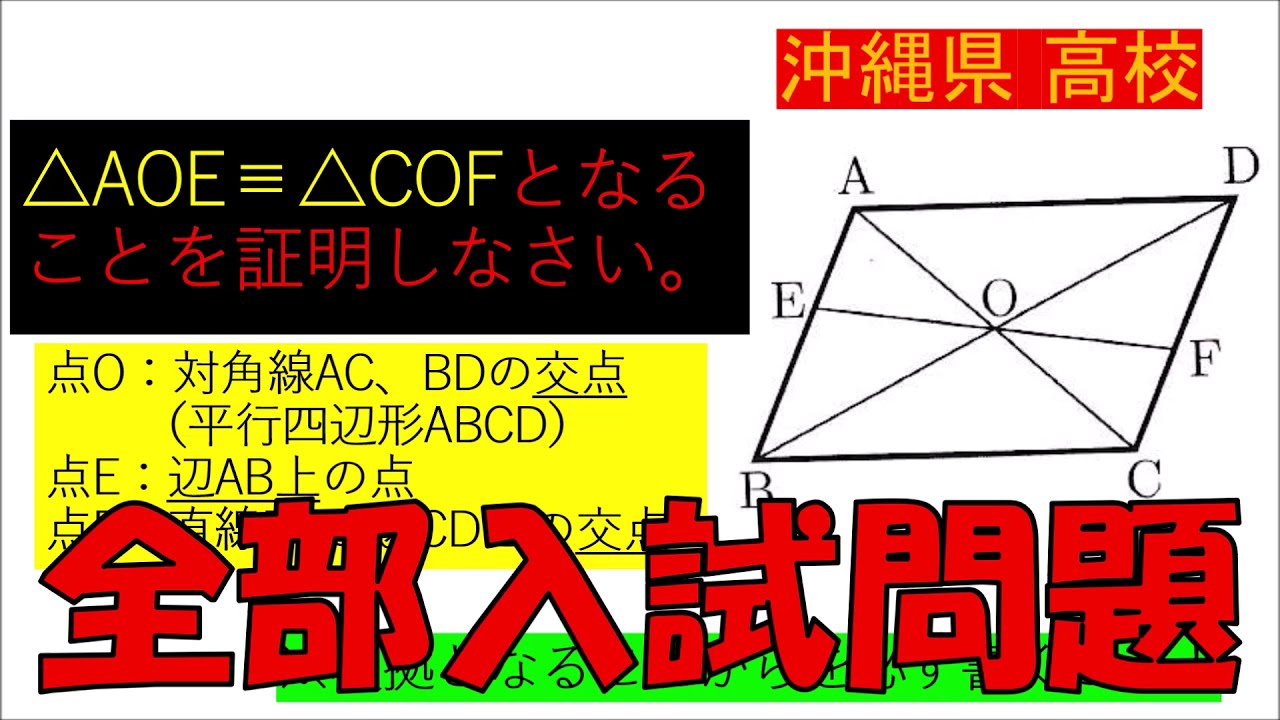
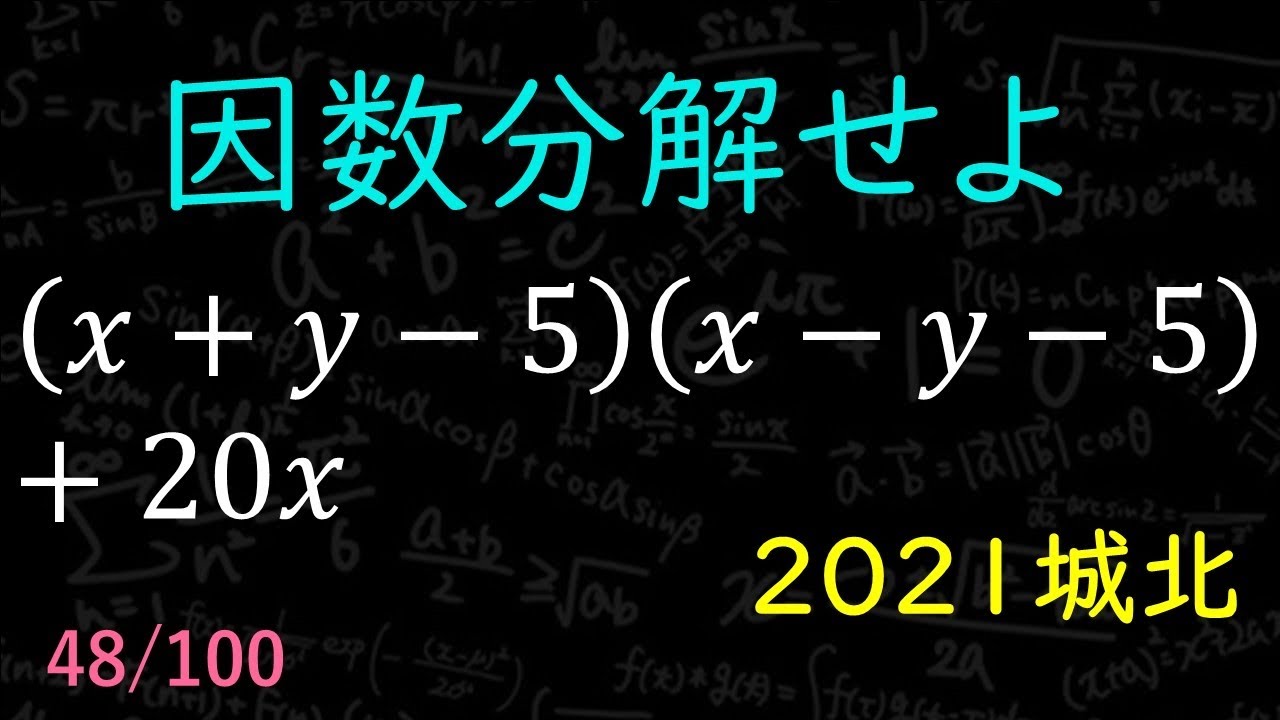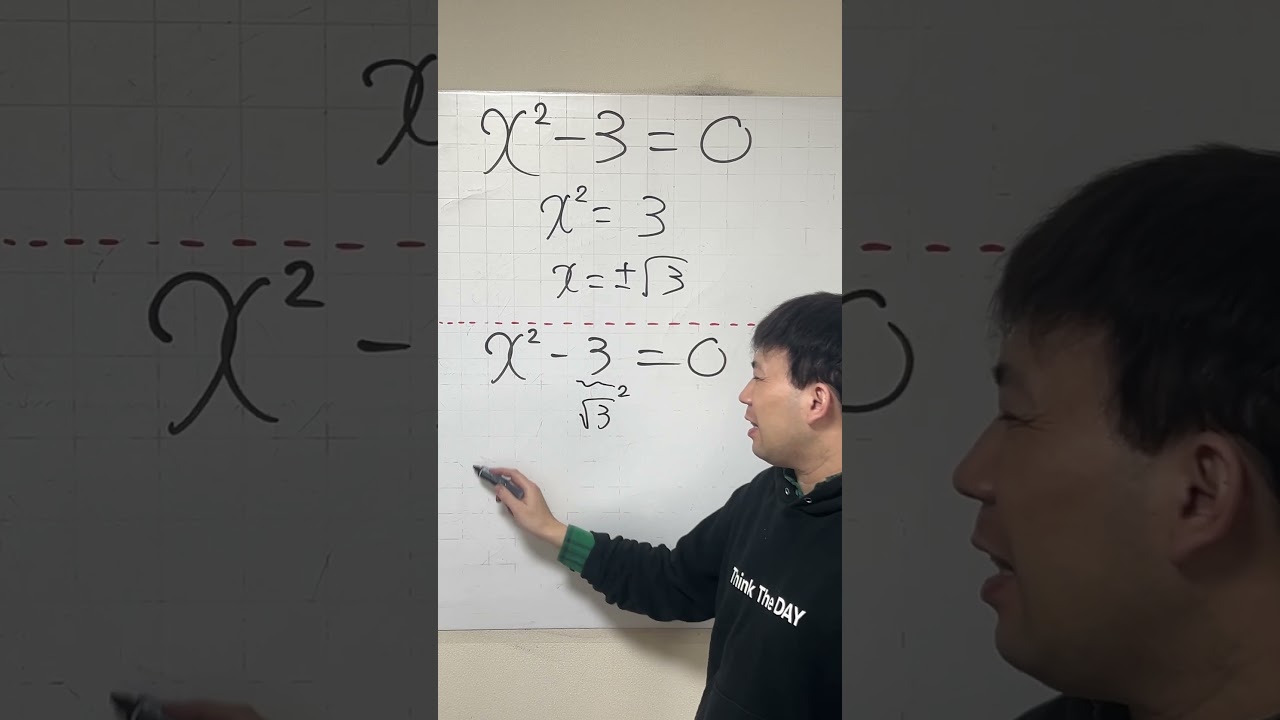問題文全文(内容文)：
二次関数といえば、y=①＿＿＿＿

◎xとyの関係を式に表そう。
②yはxの2乗に比例し、x=-2のときy=24。

③yはxの2乗に比例し、x=-4のとき、y=-8。

◎次の値をだそう。
④yはxの2乗に比例し、x=-3のときy=-4である。
x=2のとき、yの値は？

⑤yはxの2乗に比例し、x=2のときy=-3である。
y=12のときxの値は？
単元： #数学(中学生)#中３数学#2次関数
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
二次関数といえば、y=①＿＿＿＿

◎xとyの関係を式に表そう。
②yはxの2乗に比例し、x=-2のときy=24。

③yはxの2乗に比例し、x=-4のとき、y=-8。

◎次の値をだそう。
④yはxの2乗に比例し、x=-3のときy=-4である。
x=2のとき、yの値は？

⑤yはxの2乗に比例し、x=2のときy=-3である。
y=12のときxの値は？
投稿日：2013.07.27

＜関連動画＞

素因数分解　　教えて下さい たくさんのコメントありがとうございます。

アイキャッチ画像
単元： #数学(中学生)#中３数学#式の計算（展開、因数分解）
指導講師： 数学を数楽に
問題文全文(内容文)：
$7^4-2^4 \times 3^2$を素因数分解せよ。
この動画を見る　

工夫して解く平方根の計算…！～全国入試問題解法 #shorts, #数学 #高校入試, #頭の体操. #ルチルクォーツ

アイキャッチ画像
単元： #数学(中学生)#中３数学#平方根
指導講師： 高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ \sqrt{50^2-1}$を$ a\sqrt b$の形で表せ.
*aは自然数であり,bはできるだけ小さな自然数である.

福井県入試問題過去問
この動画を見る　

これも連立方程式だって分かってる!?～全国入試問題解法 #shorts #数学 #math #高校受験

アイキャッチ画像
単元： #数学(中学生)#中２数学#中３数学#連立方程式#２次方程式
指導講師： 高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x + y = 3 \\
x^2+y^2=5
\end{array}
\right.
\end{eqnarray}$ を解け.
この動画を見る　

三平方の定理の3:4:5とかの出し方

アイキャッチ画像
単元： #中３数学#三平方の定理
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
三平方の定理の3:4:5とかの出し方説明動画です
この動画を見る　

【形を変えて…！】二次方程式：東京都立墨田川高等学校～全国入試問題解法

アイキャッチ画像
単元： #数学(中学生)#中３数学#２次方程式
指導講師： 高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
二次方程式:(x-3)^2=4x^2を解け。
この動画を見る　
PAGE TOP