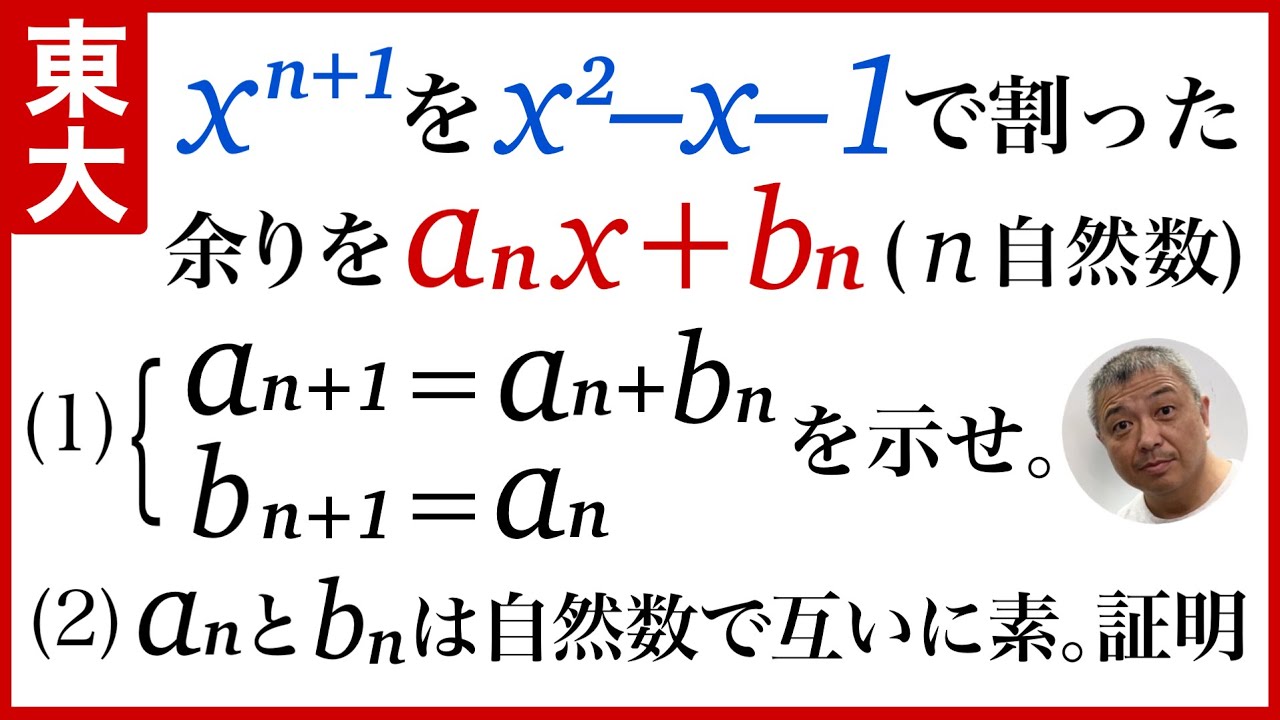問題文全文(内容文):
$\boxed{2}$
数列$\{a_n\}$に対して
$T_n=\displaystyle \sum_{k=1}^n \dfrac{(k+2)!}{(k-1)!}a_k (n=1,2,3,\cdots)$
とおくとき、
$T_n=\left(n-\dfrac{1}{2}\right)^2 (n=1,2,3,\cdots)$
が成り立つとする。ただし、$0!=1$である。
(1)$a_1=\dfrac{\boxed{ア}}{\boxed{イウ}},a_2=\dfrac{\boxed{エ}}{\boxed{オ}}$である。
(2)$n\geqq 2$に対して$T_n-T_{n-1}=\boxed{カ}n-\boxed{キ}$が
成り立つから、
$a_n=r^n\dfrac{n-\boxed{ク}}{(n+s)(n+t)(n+u)} (n=2,3,4,\cdots)$
である。ただし、ここに$r=\boxed{ケ}$であり、
$s\lt t \lt u$として$s=\boxed{コ},t=\boxed{サ},u=\boxed{シ}$である。
$2025$年慶應義塾大学経済学部過去問題
$\boxed{2}$
数列$\{a_n\}$に対して
$T_n=\displaystyle \sum_{k=1}^n \dfrac{(k+2)!}{(k-1)!}a_k (n=1,2,3,\cdots)$
とおくとき、
$T_n=\left(n-\dfrac{1}{2}\right)^2 (n=1,2,3,\cdots)$
が成り立つとする。ただし、$0!=1$である。
(1)$a_1=\dfrac{\boxed{ア}}{\boxed{イウ}},a_2=\dfrac{\boxed{エ}}{\boxed{オ}}$である。
(2)$n\geqq 2$に対して$T_n-T_{n-1}=\boxed{カ}n-\boxed{キ}$が
成り立つから、
$a_n=r^n\dfrac{n-\boxed{ク}}{(n+s)(n+t)(n+u)} (n=2,3,4,\cdots)$
である。ただし、ここに$r=\boxed{ケ}$であり、
$s\lt t \lt u$として$s=\boxed{コ},t=\boxed{サ},u=\boxed{シ}$である。
$2025$年慶應義塾大学経済学部過去問題
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
数列$\{a_n\}$に対して
$T_n=\displaystyle \sum_{k=1}^n \dfrac{(k+2)!}{(k-1)!}a_k (n=1,2,3,\cdots)$
とおくとき、
$T_n=\left(n-\dfrac{1}{2}\right)^2 (n=1,2,3,\cdots)$
が成り立つとする。ただし、$0!=1$である。
(1)$a_1=\dfrac{\boxed{ア}}{\boxed{イウ}},a_2=\dfrac{\boxed{エ}}{\boxed{オ}}$である。
(2)$n\geqq 2$に対して$T_n-T_{n-1}=\boxed{カ}n-\boxed{キ}$が
成り立つから、
$a_n=r^n\dfrac{n-\boxed{ク}}{(n+s)(n+t)(n+u)} (n=2,3,4,\cdots)$
である。ただし、ここに$r=\boxed{ケ}$であり、
$s\lt t \lt u$として$s=\boxed{コ},t=\boxed{サ},u=\boxed{シ}$である。
$2025$年慶應義塾大学経済学部過去問題
$\boxed{2}$
数列$\{a_n\}$に対して
$T_n=\displaystyle \sum_{k=1}^n \dfrac{(k+2)!}{(k-1)!}a_k (n=1,2,3,\cdots)$
とおくとき、
$T_n=\left(n-\dfrac{1}{2}\right)^2 (n=1,2,3,\cdots)$
が成り立つとする。ただし、$0!=1$である。
(1)$a_1=\dfrac{\boxed{ア}}{\boxed{イウ}},a_2=\dfrac{\boxed{エ}}{\boxed{オ}}$である。
(2)$n\geqq 2$に対して$T_n-T_{n-1}=\boxed{カ}n-\boxed{キ}$が
成り立つから、
$a_n=r^n\dfrac{n-\boxed{ク}}{(n+s)(n+t)(n+u)} (n=2,3,4,\cdots)$
である。ただし、ここに$r=\boxed{ケ}$であり、
$s\lt t \lt u$として$s=\boxed{コ},t=\boxed{サ},u=\boxed{シ}$である。
$2025$年慶應義塾大学経済学部過去問題
投稿日:2025.05.21