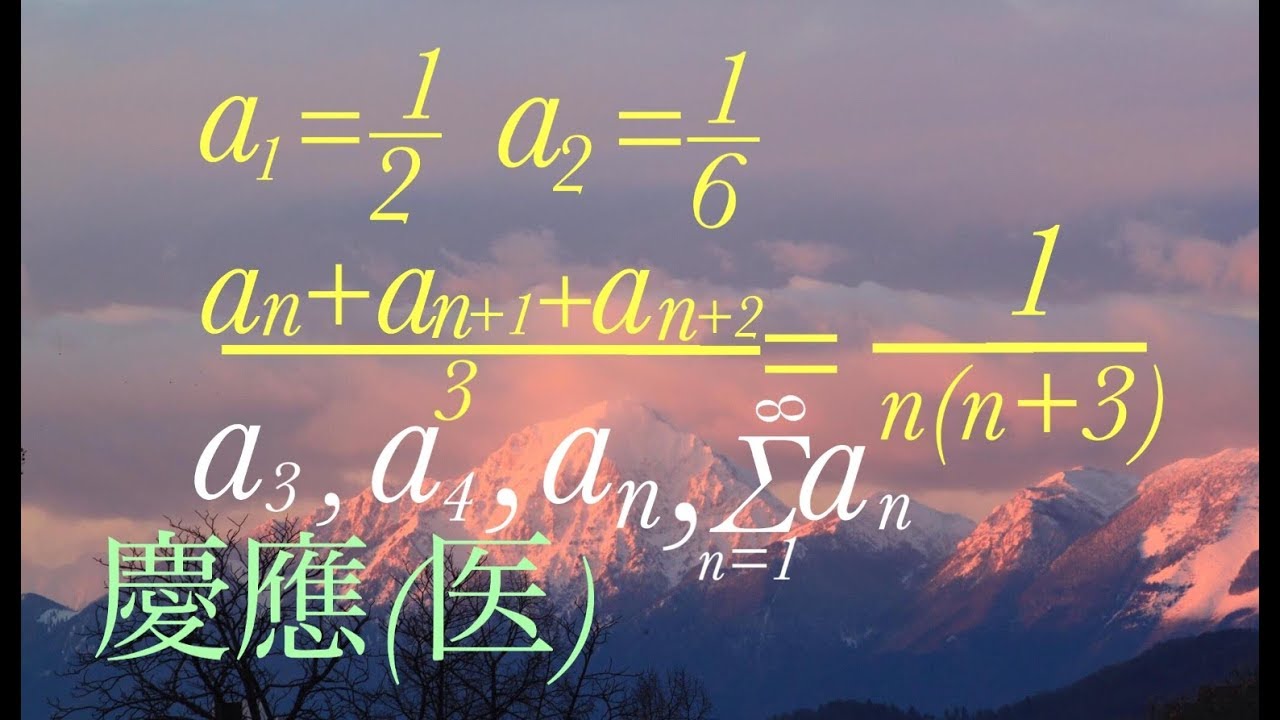問題文全文(内容文):
n自然数
$\sqrt{n}$に最も近い整数を$a_n$とする
(例)$a_3=2$,$a_{10}=3$
$\displaystyle\sum_{n=1}^{2023}\frac{1}{a_n}$を求めよ
n自然数
$\sqrt{n}$に最も近い整数を$a_n$とする
(例)$a_3=2$,$a_{10}=3$
$\displaystyle\sum_{n=1}^{2023}\frac{1}{a_n}$を求めよ
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
n自然数
$\sqrt{n}$に最も近い整数を$a_n$とする
(例)$a_3=2$,$a_{10}=3$
$\displaystyle\sum_{n=1}^{2023}\frac{1}{a_n}$を求めよ
n自然数
$\sqrt{n}$に最も近い整数を$a_n$とする
(例)$a_3=2$,$a_{10}=3$
$\displaystyle\sum_{n=1}^{2023}\frac{1}{a_n}$を求めよ
投稿日:2023.07.27