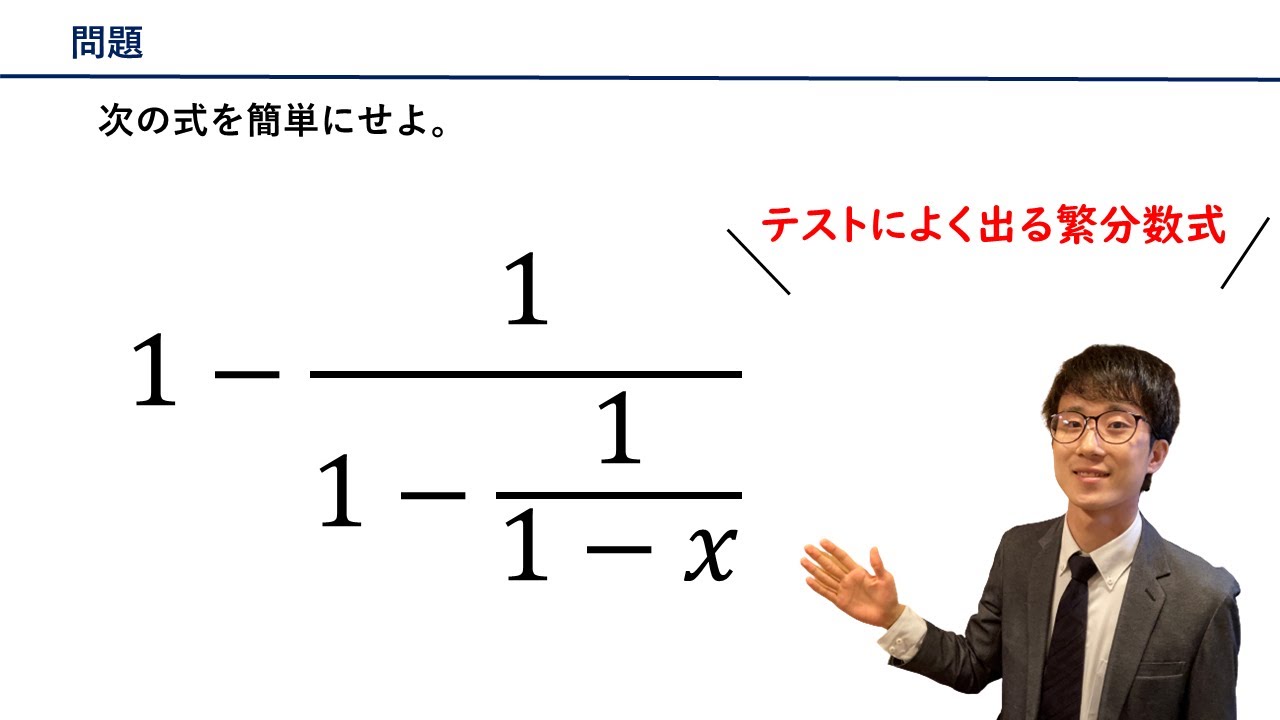大学入試問題#158 名古屋市立大学(2020) ２項展開の応用

問題文全文(内容文)：
$(x+2y)^2(x+2y+3z)^4$を展開した時
$x^4y^2,x^3y^2z$の係数をそれぞれ求めよ。

出典：2020年名古屋市立大学　入試問題

チャプター：

03:58~解答のみ掲載　約１０秒間隔

単元： #数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋市立大学

指導講師：ますただ

問題文全文(内容文)：
$(x+2y)^2(x+2y+3z)^4$を展開した時
$x^4y^2,x^3y^2z$の係数をそれぞれ求めよ。

出典：2020年名古屋市立大学　入試問題

投稿日：2022.04.02

単元： #数学(中学生)#数Ⅱ#式と証明#整式の除法・分数式・二項定理#高校入試過去問(数学)

指導講師：数学を数楽に

問題文全文(内容文)：
$\frac{\frac{1}{3} - \frac{2}{5} }
{\frac{1}{3} - \frac{2}{5} + \frac{3}{7}}$

慶應義塾高等学校

この動画を見る　

単元： #数学(中学生)#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#恒等式・等式・不等式の証明#数列#数列とその和（等差・等比・階差・Σ）#高校入試過去問(数学)#数B

指導講師：鈴木貫太郎

問題文全文(内容文)：
2022都立入試　整数問題証明に関して解説していきます.

この動画を見る　

単元： #数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$n$は自然数である.
(1)$x^n$を$x^5-1$で割った余りを求めよ.
(2)$x^{4n}+x^{3n}+x^{2n}+x^n$を$x^4+x^3+x^2+x+1$で割った余りを求めよ.

2005大分大(医)過去問

この動画を見る　

単元： #数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)#新潟大学

指導講師：ますただ

問題文全文(内容文)：
$a,b,c,d$：正の実数
$\displaystyle \frac{a+b+c+d}{4} \geqq \sqrt[ 4 ]{ abcd }$を示せ

出典：2012年新潟大学　入試問題

この動画を見る　

単元： #数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+･･･････+\dfrac{32}{33}=\dfrac{a}{33!}$
$a$を17で割った余りを求めよ.

この動画を見る　