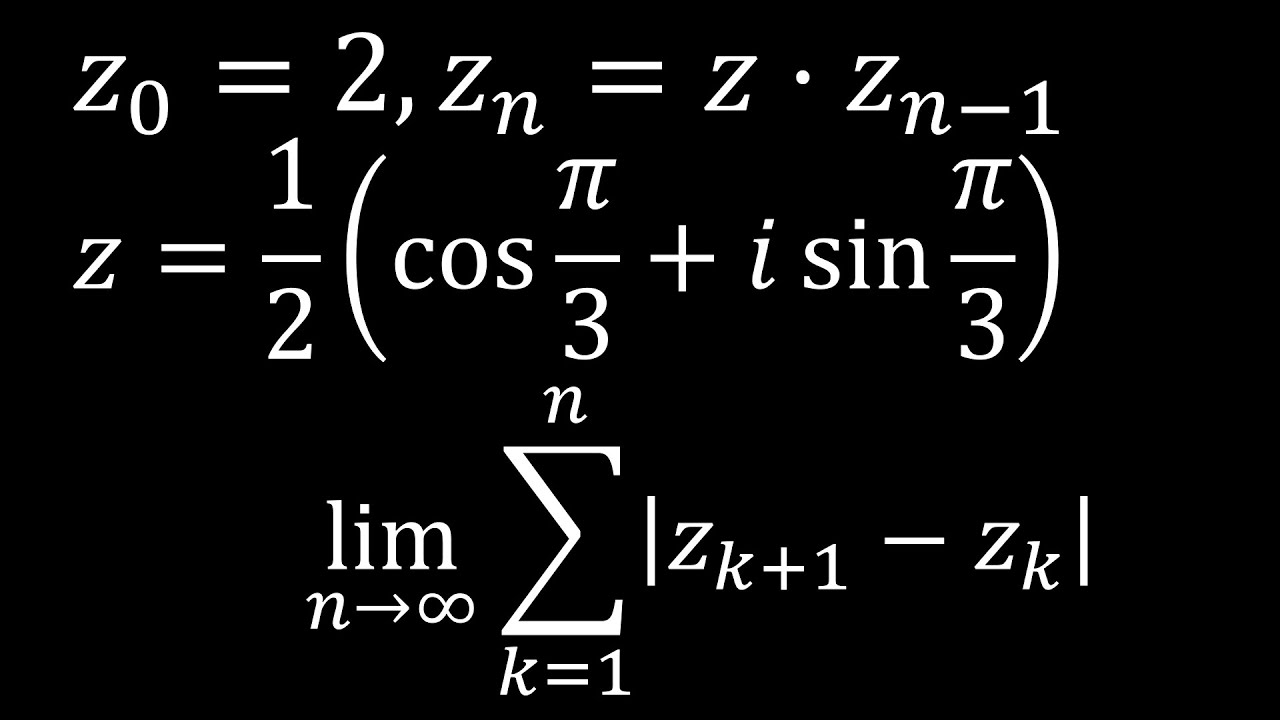3次不等式を解け

単元： #数Ⅱ#複素数と方程式#複素数

指導講師：数学を数楽に

投稿日：2024.10.02

単元： #数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数平面#複素数#複素数平面#数学検定#数学検定1級#数学(高校生)#数C

指導講師：ますただ

問題文全文(内容文)：
$\sqrt{ 1+\sqrt{ 3 }i }+\sqrt{ 1-\sqrt{ 3 }i }$を簡単にせよ
ただし、外側の平方根の実数部の値は正とする。

この動画を見る　

単元： #数Ⅱ#複素数と方程式#複素数#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
三倍角の公式を複素数の掛け算（ド・モアブルの定理）で簡単に導きます.

この動画を見る　

単元： #数Ⅱ#複素数と方程式#複素数#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
以下を求めよ。
$\sqrt{ 2 }\times\sqrt{ 3 }=??$
$\sqrt{ (-2) }\times\sqrt{ (-3) }=??$

この動画を見る　

単元： #数Ⅱ#複素数と方程式#複素数#数学(高校生)

教材： #4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#複素数と方程式#中高教材

指導講師：理数個別チャンネル

問題文全文(内容文)：
2つの複素数a+biと2-3iの和が純虚数、積が実数となるように、実数a, bの値を定めよ。

虚数α、βの和、積がともに実数ならば、α、βは互いに共役であることを示せ。

この動画を見る　

単元： #数Ⅱ#複素数と方程式#複素数#数学(高校生)

指導講師：とある男が授業をしてみた

問題文全文(内容文)：
$\boxed{1}$次の複素数の絶対値を求めよう.

③$3+i$
④$-2i$
⑤$1-\sqrt3$

$\boxed{2}$次の2点間の距離を求めよう.

⑥$A(5-2i),B(1-i)$
⑦$A(-1-3i),B(3-5i)$

この動画を見る　