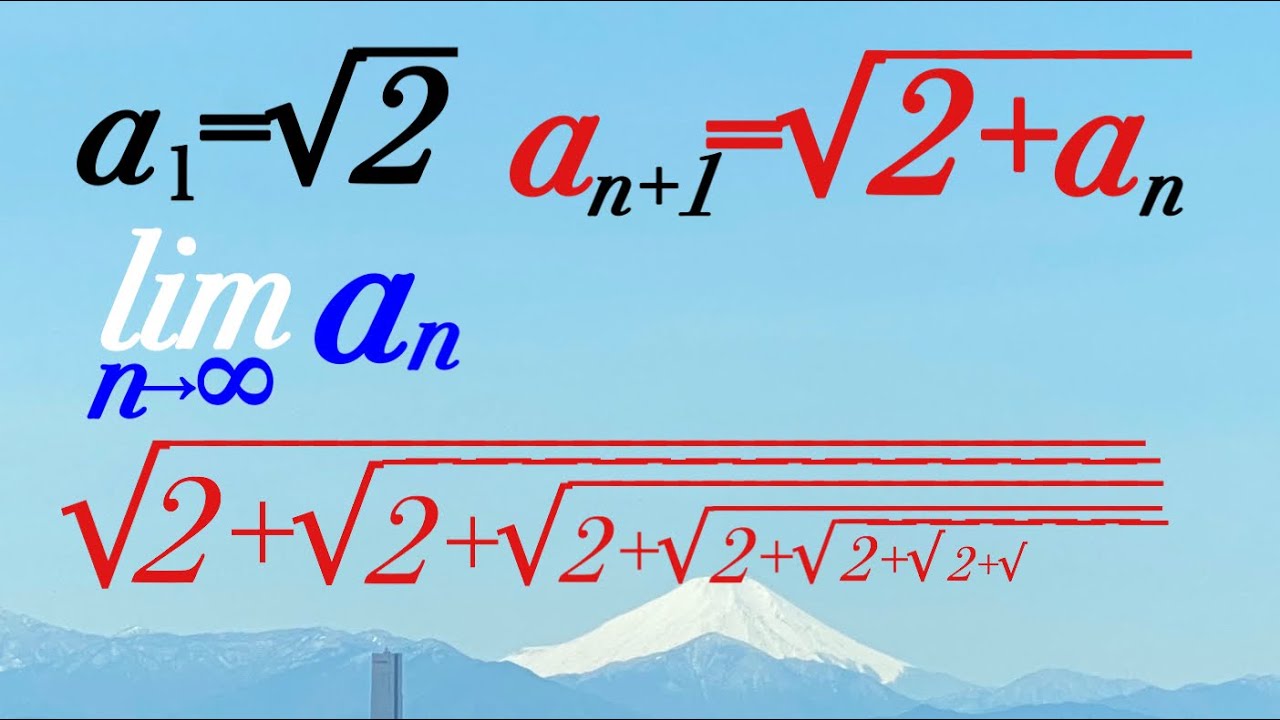これの説明できますか？

問題文全文(内容文)：
1-1-+1-1-+1-1...
解説動画です

単元： #数列#漸化式#数列の極限#数学(高校生)#数B#数Ⅲ

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
1-1-+1-1-+1-1...
解説動画です

投稿日：2022.04.18

＜関連動画＞

【0から理解できる】数学B・数列和の記号Σ②（等比数列の和）

単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B

指導講師：【ゼロから理解できる】高校数学・物理

問題文全文(内容文)：
次の和を求めよ。
（1）
$\displaystyle \sum_{k=1}^7 2^k$

（2）
$\displaystyle \sum_{k=1}^{n-1} 3^k$

（3）
$\displaystyle \sum_{k=1}^n 3・(-2)^k$

この動画を見る　

【数B】数列：等差×等比型の数列和！　∑[k=1からn]k・2^kの和を求めよ。

単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)

指導講師：理数個別チャンネル

問題文全文(内容文)：
$\displaystyle \sum_{k\to1}^k・2^k$の和を求めよ.

この動画を見る　

数列の収束

単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B

指導講師：鈴木貫太郎

問題文全文(内容文)：
数列の収束に関して解説していきます.

この動画を見る　

例のアレ

単元： #数列とその和（等差・等比・階差・Σ）

指導講師：鈴木貫太郎

問題文全文(内容文)：
$\displaystyle \frac{1}{1×2×3×4}＋\displaystyle \frac{1}{2×3×4×5}+\displaystyle \frac{1}{3×4×5×6}$$＋…+\displaystyle \frac{1}{6×7×8×9}＋\displaystyle \frac{1}{7×8×9×10}$

この動画を見る　

【数学B/テスト対策】等比数列の一般項と和

単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B

指導講師：【ゼロから理解できる】高校数学・物理

問題文全文(内容文)：
等比数列$-2,6,-18,54,…$について、次の問いに答えよ。
（1）
一般項$a_n$を求めよ。

（2）
初項から第$n$項までの和$S_n$を求めよ。

（3）
初項から第$5$項までの和$S_5$を求めよ。

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> これの説明できますか？

＜関連動画＞

【0から理解できる】数学B・数列 和の記号Σ②（等比数列の和）

【数B】数列： 等差×等比型の数列和！ ∑[k=1からn]k・2^kの和を求めよ。

数列の収束

例のアレ

【数学B/テスト対策】等比数列の一般項と和