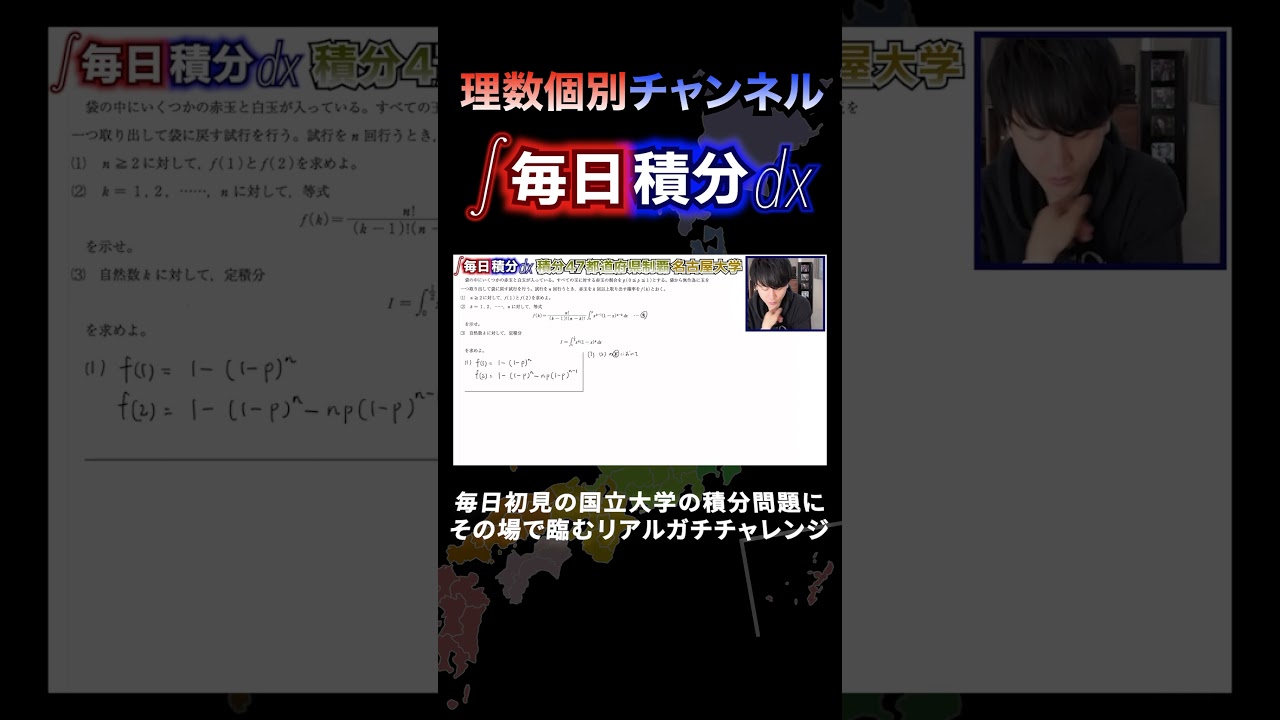
問題文全文(内容文):
確率の求め方で、間違った数え方していませんか?
確率の計算方法について解説します。
大小二つのサイコロを振った時、目の合計が3になる確率は?
二つのサイコロを振った時、目の合計が3になる確率は?
答えに違いはある??
確率の求め方で、間違った数え方していませんか?
確率の計算方法について解説します。
大小二つのサイコロを振った時、目の合計が3になる確率は?
二つのサイコロを振った時、目の合計が3になる確率は?
答えに違いはある??
チャプター:
0:00 OP
0:06 本編
2:40 ED
単元:
#数学(中学生)#中2数学#数A#場合の数と確率#確率#確率#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
確率の求め方で、間違った数え方していませんか?
確率の計算方法について解説します。
大小二つのサイコロを振った時、目の合計が3になる確率は?
二つのサイコロを振った時、目の合計が3になる確率は?
答えに違いはある??
確率の求め方で、間違った数え方していませんか?
確率の計算方法について解説します。
大小二つのサイコロを振った時、目の合計が3になる確率は?
二つのサイコロを振った時、目の合計が3になる確率は?
答えに違いはある??
投稿日:2023.02.08