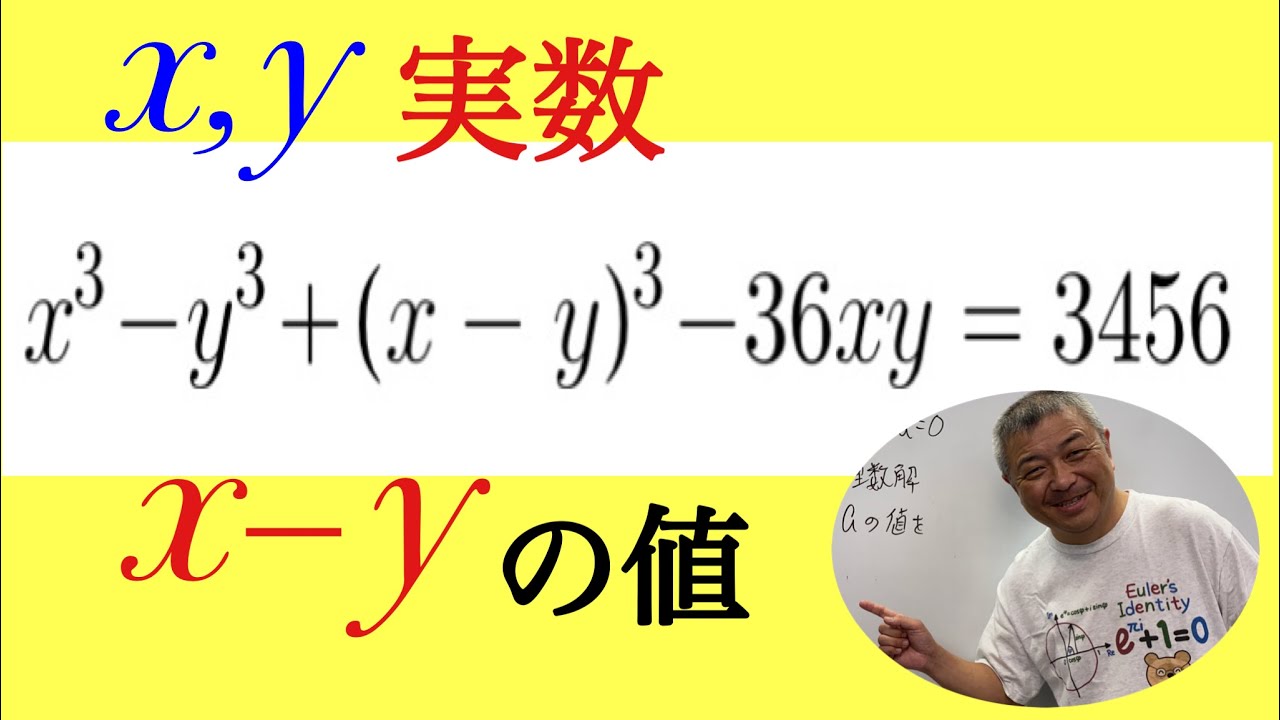問題文全文(内容文):
2⃣$x^3-7x^2-4x+1=0$
の3つの解をα、β、γとする。
$α^2+β^2+γ^2$の値を求めよ。
解と係数の関係
$ax^3+bx^2+cx+d=0$
$α+β+γ=- \frac{b}{a}$
$αβ+βγ+γα=\frac{c}{a}$
$αβγ=- \frac{d}{a}$
2⃣$x^3-7x^2-4x+1=0$
の3つの解をα、β、γとする。
$α^2+β^2+γ^2$の値を求めよ。
解と係数の関係
$ax^3+bx^2+cx+d=0$
$α+β+γ=- \frac{b}{a}$
$αβ+βγ+γα=\frac{c}{a}$
$αβγ=- \frac{d}{a}$
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#解と判別式・解と係数の関係#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
2⃣$x^3-7x^2-4x+1=0$
の3つの解をα、β、γとする。
$α^2+β^2+γ^2$の値を求めよ。
解と係数の関係
$ax^3+bx^2+cx+d=0$
$α+β+γ=- \frac{b}{a}$
$αβ+βγ+γα=\frac{c}{a}$
$αβγ=- \frac{d}{a}$
2⃣$x^3-7x^2-4x+1=0$
の3つの解をα、β、γとする。
$α^2+β^2+γ^2$の値を求めよ。
解と係数の関係
$ax^3+bx^2+cx+d=0$
$α+β+γ=- \frac{b}{a}$
$αβ+βγ+γα=\frac{c}{a}$
$αβγ=- \frac{d}{a}$
投稿日:2020.11.30