【数学】中2-46 対頂角同位角錯角② 問題編

問題文全文(内容文)：
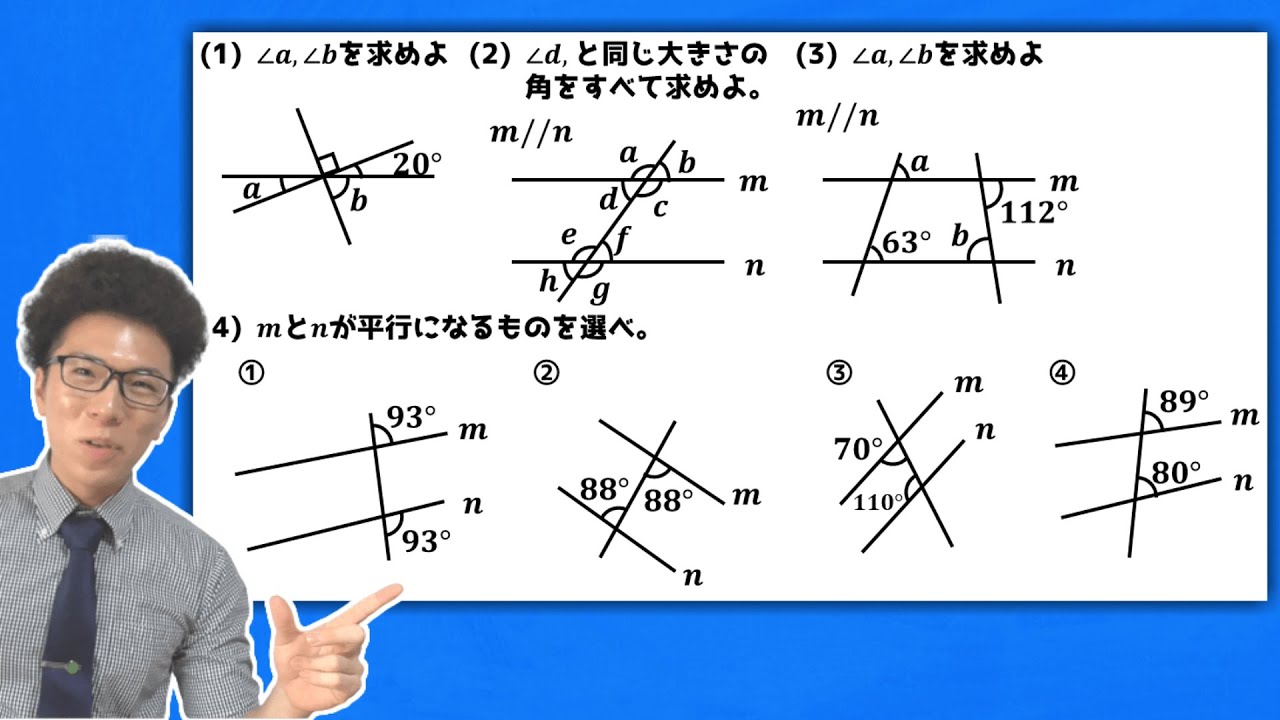
◎ℓ//mのとき、$\angle x,\angle y $の大きさを求めよう！
※図は動画内参照

単元： #数学(中学生)#中２数学#平行と合同#三角形と四角形

指導講師：とある男が授業をしてみた

問題文全文(内容文)：
◎ℓ//mのとき、$\angle x,\angle y $の大きさを求めよう！
※図は動画内参照

投稿日：2013.10.28

単元： #数学(中学生)#中２数学#1次関数#高校入試過去問(数学)#函館ラ・サール高等学校

指導講師：高校入試から見た数学の世界「全部入試問題」by しろたん

問題文全文(内容文)：
1次関数$ y=ax+3(a \lt 0)$
$ -2 \leqq x \leqq 5 $であるとき,$ -2 \leqq y \leqq b $となるような
$ a $と$ b $の値を求めなさい.

函館ラサール高校過去問

この動画を見る　

単元： #数学(中学生)#中１数学#中２数学#平面図形#三角形と四角形#高校入試過去問(数学)

指導講師：数学を数楽に

問題文全文(内容文)：
n=?
＊図は動画内参照

2022立教新座高等学校（改）

この動画を見る　

単元： #数学(中学生)#中２数学#式の計算（単項式・多項式・式の四則計算）

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
０で割れると成り立つ不思議な世界についての動画です

この動画を見る　

単元： #数学(中学生)#中２数学#三角形と四角形

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
1⃣
十五角形の内角の和を求めよ。

2⃣
正八角形の1つの内角の大きさを答えよ。

3⃣
1つの内角の大きさが150$^{ \circ }$である正多角形は何角形か。

この動画を見る　

単元： #連立方程式

指導講師：数学を数楽に

問題文全文(内容文)：
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y +2z= 2 \\
x + 2y +z= 7 \\
2x + y + z = -1
\end{array}
\right.
\end{eqnarray}

この動画を見る　