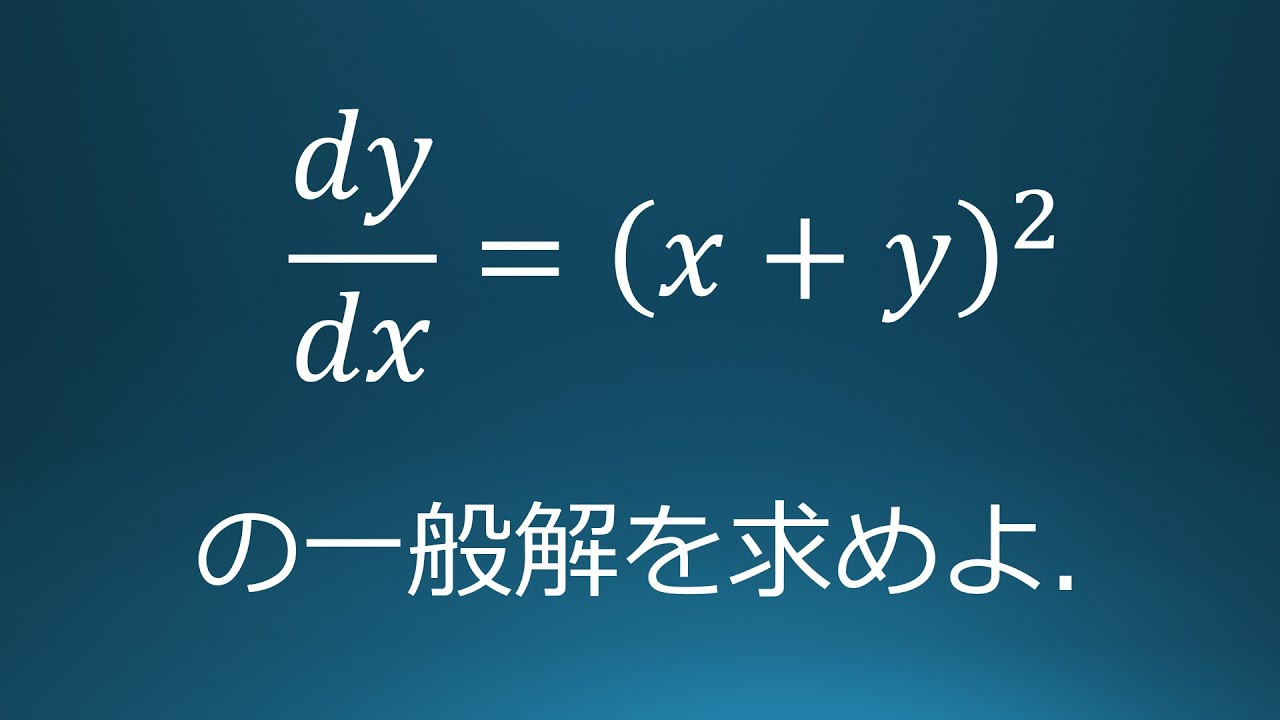問題文全文(内容文):
$Z \in A \not \subset $
次の方程式を解け.
(1)$Z^6=1$
(2)$Z^4=-1$
(3)$Z^3=8i$
「$Z・r(\cos\theta+i\sin\theta)$
$r\geqq 0,0\leqq \theta \lt 2\pi」$
$Z \in A \not \subset $
次の方程式を解け.
(1)$Z^6=1$
(2)$Z^4=-1$
(3)$Z^3=8i$
「$Z・r(\cos\theta+i\sin\theta)$
$r\geqq 0,0\leqq \theta \lt 2\pi」$
単元:
#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$Z \in A \not \subset $
次の方程式を解け.
(1)$Z^6=1$
(2)$Z^4=-1$
(3)$Z^3=8i$
「$Z・r(\cos\theta+i\sin\theta)$
$r\geqq 0,0\leqq \theta \lt 2\pi」$
$Z \in A \not \subset $
次の方程式を解け.
(1)$Z^6=1$
(2)$Z^4=-1$
(3)$Z^3=8i$
「$Z・r(\cos\theta+i\sin\theta)$
$r\geqq 0,0\leqq \theta \lt 2\pi」$
投稿日:2021.02.07