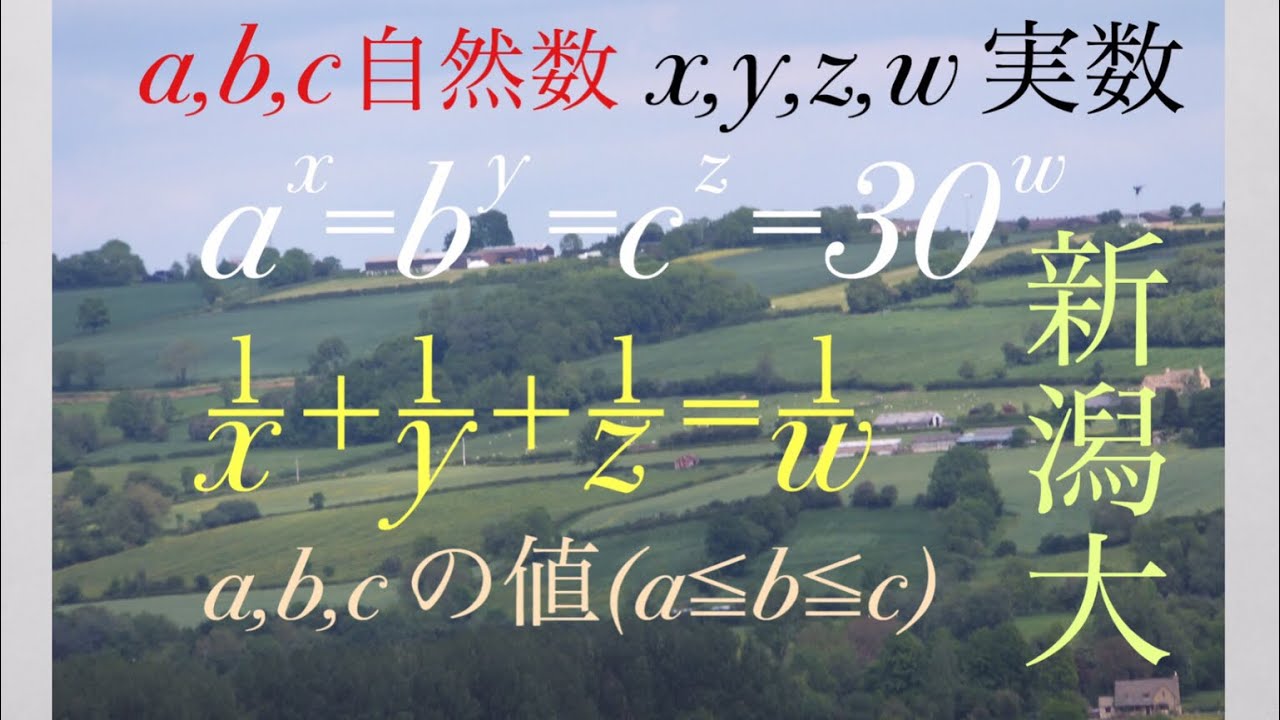問題文全文(内容文):
$a,b,c,d:$自然数
$a \lt b \lt c \lt d$
$\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b}+\displaystyle \frac{1}{c}+\displaystyle \frac{1}{d}=2$を満たすとき$a+b+c+d$の値を求めよ
$a,b,c,d:$自然数
$a \lt b \lt c \lt d$
$\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b}+\displaystyle \frac{1}{c}+\displaystyle \frac{1}{d}=2$を満たすとき$a+b+c+d$の値を求めよ
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$a,b,c,d:$自然数
$a \lt b \lt c \lt d$
$\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b}+\displaystyle \frac{1}{c}+\displaystyle \frac{1}{d}=2$を満たすとき$a+b+c+d$の値を求めよ
$a,b,c,d:$自然数
$a \lt b \lt c \lt d$
$\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b}+\displaystyle \frac{1}{c}+\displaystyle \frac{1}{d}=2$を満たすとき$a+b+c+d$の値を求めよ
投稿日:2021.11.12