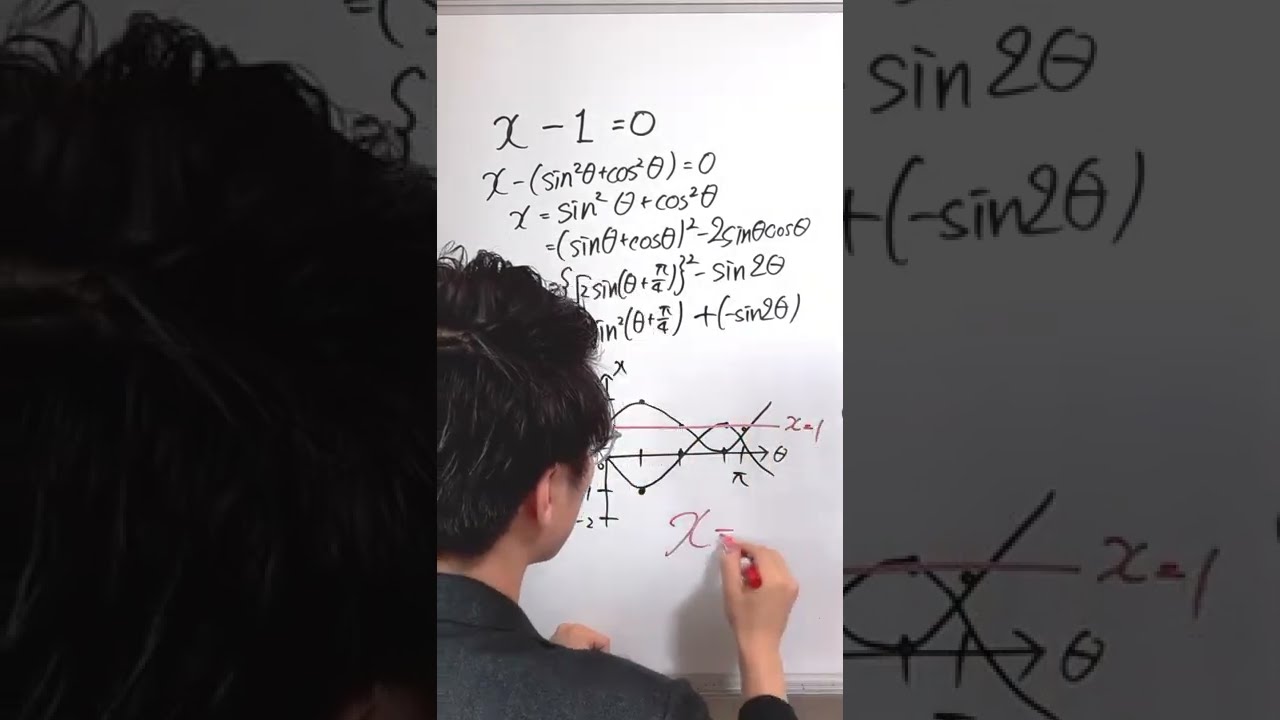【数B】数列：次の条件を満たす等差数列anの一般項を求めよ。a1+a4=12,a1+a7=18

問題文全文(内容文)：
次の条件を満たす等差数列anの一般項を求めよ。
a1+a4=12,a1+a7=18

チャプター：

0:00 オープニング
0:05 問題解説
1:57 名言

単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)

指導講師：理数個別チャンネル

問題文全文(内容文)：
次の条件を満たす等差数列anの一般項を求めよ。
a1+a4=12,a1+a7=18

投稿日：2020.06.17

単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)

指導講師：理数個別チャンネル

問題文全文(内容文)：
$\displaystyle \sum_{k\to1}^k・2^k$の和を求めよ.

この動画を見る　

単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B

指導講師：福田次郎

問題文全文(内容文)：
$\displaystyle \sum_{k=1}^n \frac {5^k(4k-1)}{k(k+1)}$を求めよ。

この動画を見る　

単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B

指導講師：数学を数楽に

問題文全文(内容文)：
4!=
3!=
2!=
1!=
0!=

この動画を見る　

単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B

教材： #4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#中高教材#数列

指導講師：理数個別チャンネル

問題文全文(内容文)：
nは自然数とする。座標平面上の3点(0,0),(3n,0)(0,n)を頂点とする三角形の周および内部にある格子点の個数を求めよ。

この動画を見る　

単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
次の等差数列の和を求めよ。
(1)初項100,末項30,項数7
(2)初項50,公差-4,項数n
(3)100,105,110,…,200

この動画を見る　