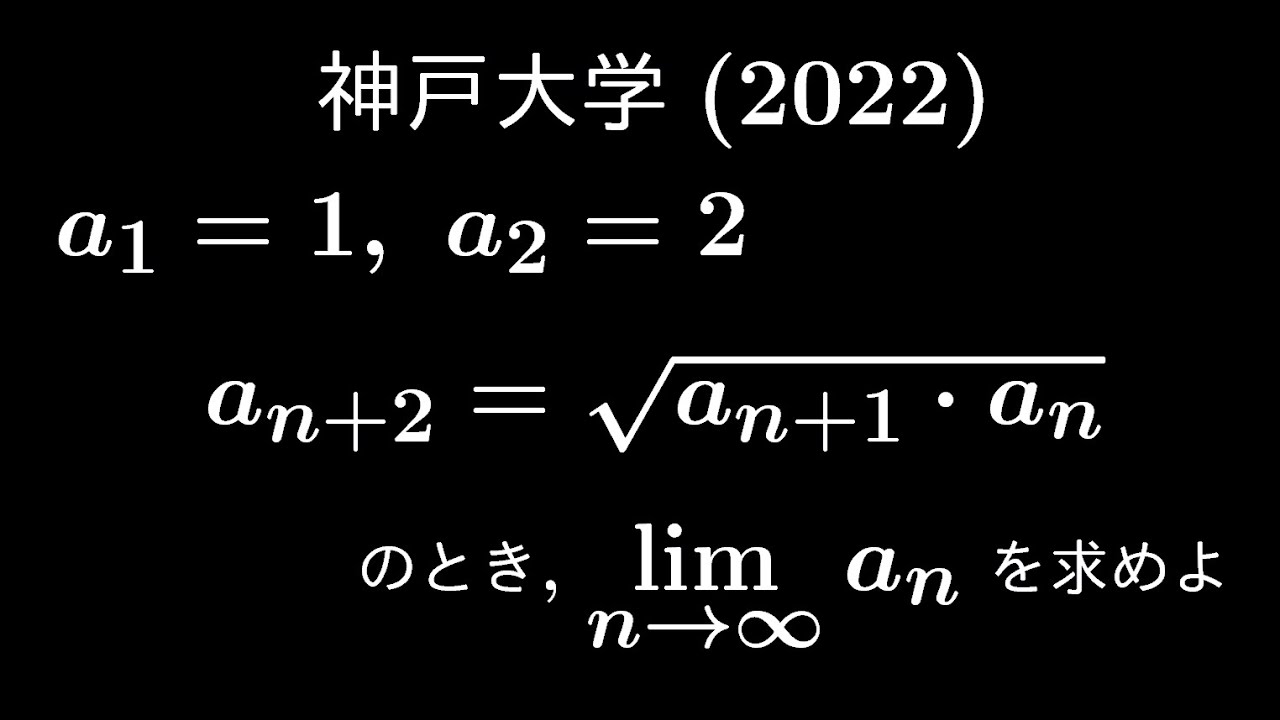問題文全文(内容文):
$n$は自然数である.
$f(n)$を$n!$の末尾に並ぶ$0$の個数とする.
(例)$f(10)=2,f(100)=24$
$\displaystyle \lim_{n\to\infty}\dfrac{f(10^n)}{10^n}$を求めよ.
1991東工大過去問
$n$は自然数である.
$f(n)$を$n!$の末尾に並ぶ$0$の個数とする.
(例)$f(10)=2,f(100)=24$
$\displaystyle \lim_{n\to\infty}\dfrac{f(10^n)}{10^n}$を求めよ.
1991東工大過去問
単元:
#関数と極限#数列の極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数である.
$f(n)$を$n!$の末尾に並ぶ$0$の個数とする.
(例)$f(10)=2,f(100)=24$
$\displaystyle \lim_{n\to\infty}\dfrac{f(10^n)}{10^n}$を求めよ.
1991東工大過去問
$n$は自然数である.
$f(n)$を$n!$の末尾に並ぶ$0$の個数とする.
(例)$f(10)=2,f(100)=24$
$\displaystyle \lim_{n\to\infty}\dfrac{f(10^n)}{10^n}$を求めよ.
1991東工大過去問
投稿日:2020.06.30