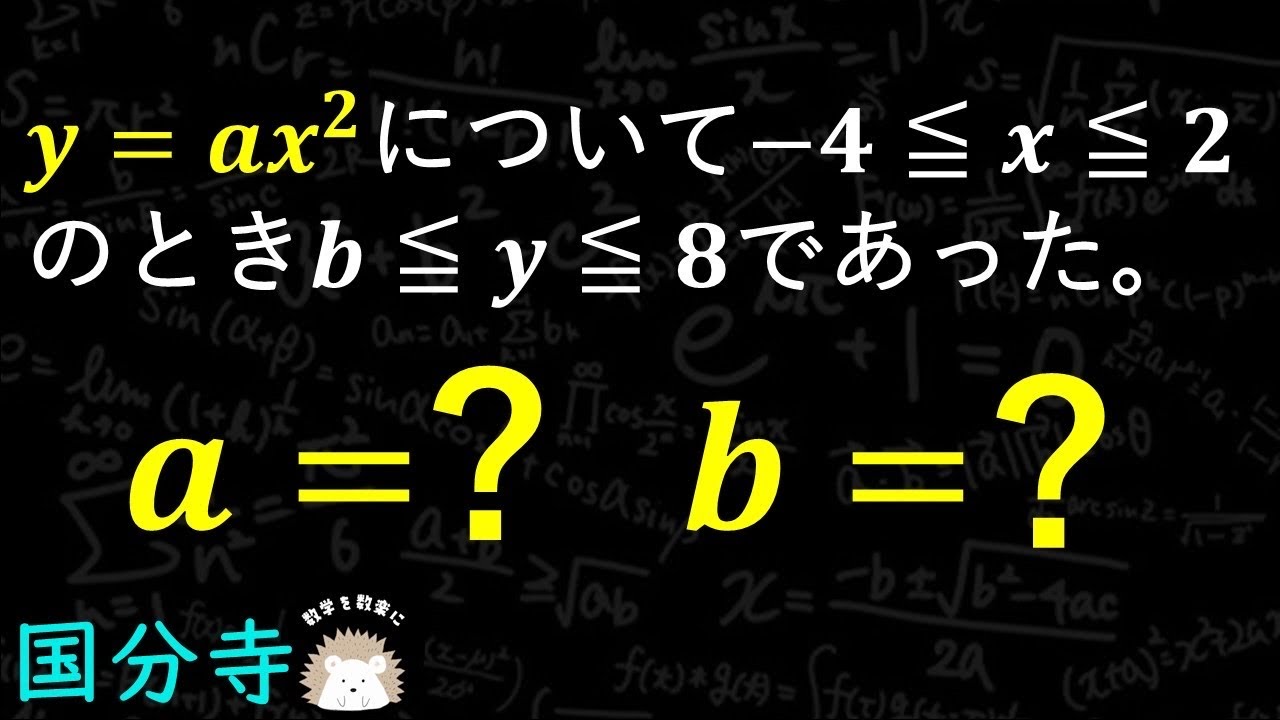平方根の計算工夫せよ久留米大附設 - 質問解決D.B.（データベース）

問題文全文(内容文)：
$(\sqrt {33} + \sqrt {21})(\sqrt {77} - 7)=$

久留米大附設高等学校

単元： #数学(中学生)#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#高校入試過去問(数学)#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
$(\sqrt {33} + \sqrt {21})(\sqrt {77} - 7)=$

久留米大附設高等学校

投稿日：2021.07.02

単元： #数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)

教材： #TK数学#TK数学問題集3(論理・確率編)#中高教材

指導講師：理数個別チャンネル

問題文全文(内容文)：
A=｛2,4,x-1｝,B=｛3,2x-y-1｝,C=｛2,2x+z-2｝とする。
B⊂A、B=Cが成り立つとき、x,y,zの値を求めよう。

この動画を見る　

単元： #数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：
\begin{eqnarray}
数学\textrm{I}　部屋割り論法(2)\\
座標平面上で異なる5個の格子点の\\
どれか2個を結ぶと、その中点が格子点になることを証明せよ。
\end{eqnarray}

この動画を見る　

単元： #数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
$y=x^2-2x+2$の最大値と最小値を求めよ

この動画を見る　

単元： #数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)

教材： #中高教材

指導講師：理数個別チャンネル

問題文全文(内容文)：
$\sqrt{\dfrac{1}{24}},\dfrac{1}{5},\sqrt{\dfrac{1}{20}},\dfrac{1}{6}$の大小を比較せよ。

この動画を見る　

単元： #数Ⅰ#数Ⅱ#２次関数#2次方程式と2次不等式#図形と方程式#軌跡と領域#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：
数学$\textrm{II}$対称式と領域(1)
実数$x,\ yがx^2+y^2 \leqq 1$を
満たしながら動くとき、
次の点の存在範囲を図示せよ。
(1)$P(x+y,\ x-y)　　(2)Q(x+y,\ xy)$

この動画を見る　