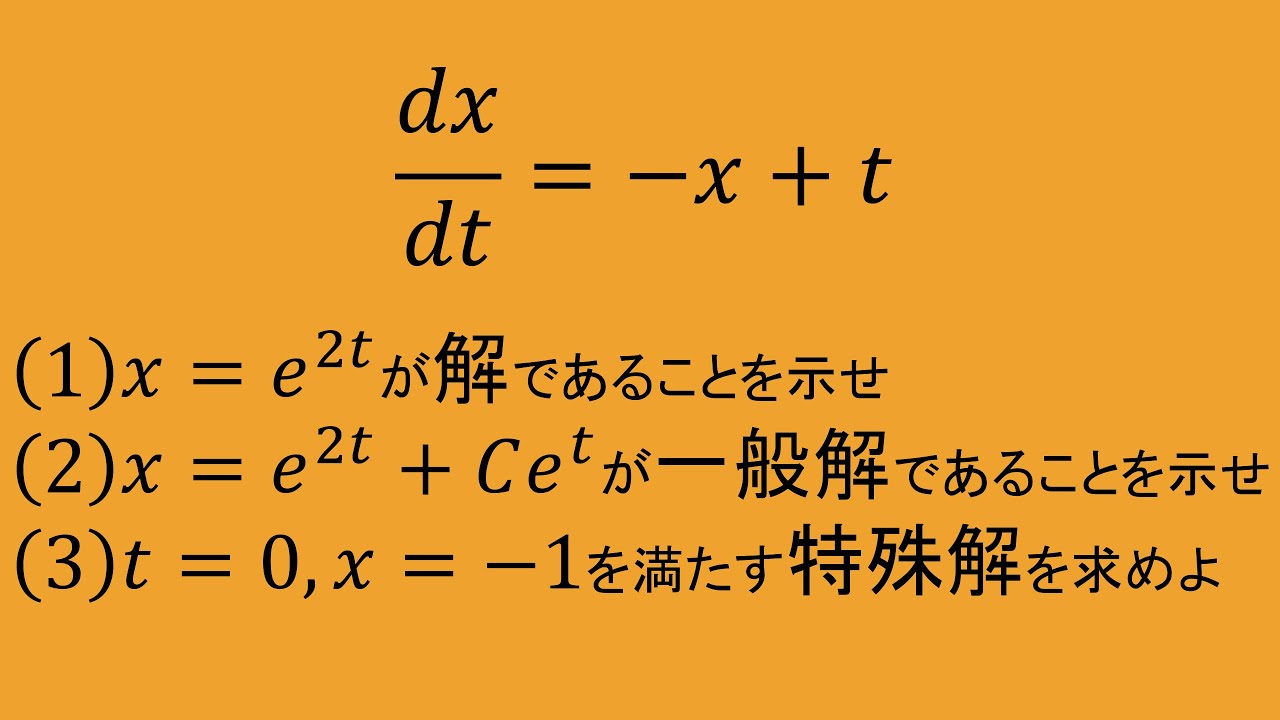問題文全文(内容文):
数Ⅲ(微分の方程式への応用)
$a$を定数とするとき、次の$x$についての方程式の異なる実数解の個数を調べよ。
①$e^x=x+a$
②$2x^3-ax^2+1$
数Ⅲ(微分の方程式への応用)
$a$を定数とするとき、次の$x$についての方程式の異なる実数解の個数を調べよ。
①$e^x=x+a$
②$2x^3-ax^2+1$
単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数Ⅲ(微分の方程式への応用)
$a$を定数とするとき、次の$x$についての方程式の異なる実数解の個数を調べよ。
①$e^x=x+a$
②$2x^3-ax^2+1$
数Ⅲ(微分の方程式への応用)
$a$を定数とするとき、次の$x$についての方程式の異なる実数解の個数を調べよ。
①$e^x=x+a$
②$2x^3-ax^2+1$
投稿日:2019.04.06