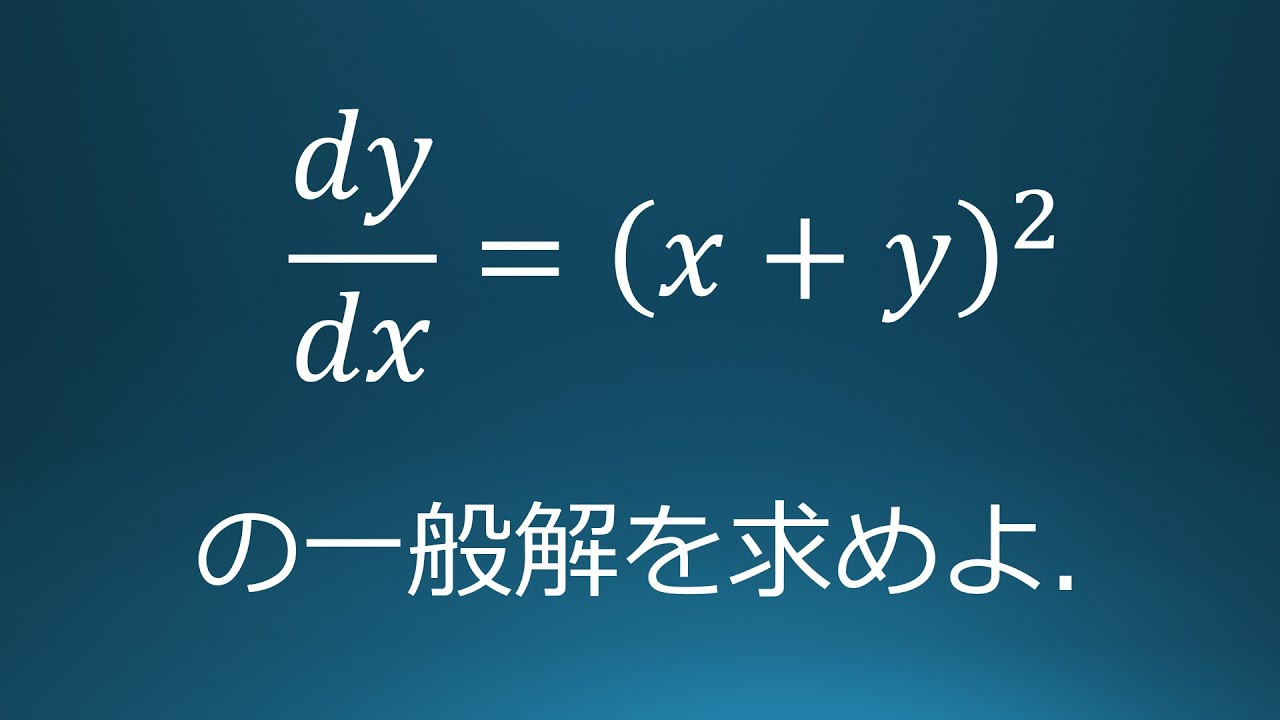【数Ⅲ】【微分とその応用】n次導関数と微分の表し方 ※問題文は概要欄

問題文全文(内容文)：
次の関数について,

\frac{d y}{d x}

を求めよ。ただし (1)(2)では

y

を用いて表してもよい。また(3)(4)では、t$$ の関数として表せ。

a, b

は正の定数とする。

x ² + 3 x y - y ² = 1

x

の関数

y

が、

t

を媒介変数として

x = c o s t + t s i n t, y = s i n t - t c o s t

と表せるとき、

\frac{d^{2} y}{d x^{2}}

を

t

の関数として表せ。

単元： #微分とその応用#微分法#色々な関数の導関数#数学(高校生)#数Ⅲ

教材： #4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用

指導講師：理数個別チャンネル

問題文全文(内容文)：
次の関数について,

\frac{d y}{d x}

を求めよ。ただし (1)(2)では

y

を用いて表してもよい。また(3)(4)では、t$$ の関数として表せ。

a, b

は正の定数とする。

x ² + 3 x y - y ² = 1

x

の関数

y

が、

t

を媒介変数として

x = c o s t + t s i n t, y = s i n t - t c o s t

と表せるとき、

\frac{d^{2} y}{d x^{2}}

を

t

の関数として表せ。

投稿日：2025.02.15

＜関連動画＞

福田の数学〜千葉大学2022年理系第９問〜関数が常に増加する条件

単元： #数Ⅰ#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ

指導講師：福田次郎

問題文全文(内容文)：
rを正の実数とし、関数

f (x) = x + \frac{r}{\sqrt{1 + \sin^{2} x}}

を考える。
(1)

r = 1

のとき、f

(x)

は常に増加することを示せ。
(2)次の条件を満たす最大の正の実数cを求めよ。

条件:

0 < r < c

のときは

f (x)

が常に増加する。

2022千葉大学理系過去問

この動画を見る　

大学入試問題#441「見た目と違って解いてみたら、良問と実感するはず！」　信州大学(2022)　#不等式

単元： #大学入試過去問(数学)#微分とその応用#色々な関数の導関数#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：

n

：自然数

0 ≦ x

：実数

l o g (1 + x) ≧ \sum_{k = 1}^{2 n} \frac{(- 1)^{k - 1}}{k} x^{k}

を示せ

出典：2022年信州大学　入試問題

この動画を見る　

福田の数学・入試問題解説〜東北大学2022年理系第２問〜4次関数の極値と最小値

単元： #数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#指数関数#接線と増減表・最大値・最小値#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ

指導講師：福田次郎

問題文全文(内容文)：
aを実数とし、実数xの関数

f (x) = (x^{2} + 3 x + a) (x + 1)^{2}

を考える。
(1)f(x)の最小値が負となるようなaのとりうる値の範囲を求めよ。
(2)

a < 2

のとき、f(x)は2つの極小値をもつ。このときf(x)が極小となる
xの値を

α_{1}, α_{2} (α_{1} < α_{2})

とする。

f (α_{1}) < f (α_{2})

を示せ。
(3)f(x)が

x < β

において単調減少し、かつ、

x = β

において最小値をとるとする。
このとき、aのとりうる値の範囲を求めよ。

2022東北大学理系過去問

この動画を見る　

数学「大学入試良問集」【18−7 球に外接する直円錐の最小体積】を宇宙一わかりやすく

単元： #大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京学芸大学

指導講師：ハクシ高校【数学科】良問演習チャンネル

問題文全文(内容文)：
半径

a

の球に外接する直円錐について、次の各問いに答えよ。
（1）直円錐の底面の半径を

x

とするとき、その高さを

x

を用いて表せ。
（2）このような直円錐の体積の最小値を求めよ。

この動画を見る　

19奈良県教員採用試験（数学：高校1番　微分）

単元： #微分とその応用#微分法#その他#数学(高校生)#数Ⅲ#教員採用試験

指導講師：ますただ

問題文全文(内容文)：
高

類題

f (x) = x s i n x が x = a で 微 分 可 能 を 示 せ

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> 【数Ⅲ】【微分とその応用】n次導関数と微分の表し方 ※問題文は概要欄

＜関連動画＞

福田の数学〜千葉大学2022年理系第９問〜関数が常に増加する条件

大学入試問題#441「見た目と違って解いてみたら、良問と実感するはず！」 信州大学(2022) #不等式

福田の数学・入試問題解説〜東北大学2022年理系第２問〜4次関数の極値と最小値

数学「大学入試良問集」【18−7 球に外接する直円錐の最小体積】を宇宙一わかりやすく

19奈良県教員採用試験（数学：高校1番 微分）