 【楽しい授業動画】あきとんとん
【楽しい授業動画】あきとんとん
 【楽しい授業動画】あきとんとん
【楽しい授業動画】あきとんとん
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
解説できる?

中学校では教えてくれない?

これ解けましたか?

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$5^x=7^y=1225$
$\displaystyle \frac{xy}{x+y}$の値を求めよ
この動画を見る
$5^x=7^y=1225$
$\displaystyle \frac{xy}{x+y}$の値を求めよ
これ解ける?

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$5^x=7^y=1225$
$\displaystyle \frac{xy}{x+y}$の値を求めよ
この動画を見る
$5^x=7^y=1225$
$\displaystyle \frac{xy}{x+y}$の値を求めよ
化学反応式これだけ!

1秒の定義ってなんですか?

計算の裏技

どう覚えた?

忘れ物の問題の裏技

単元:
#数学(中学生)#中1数学#方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
弟が5km離れた学校に向かって家を出た。
弟の忘れ物に気づいた兄は、その8分後に家を出て、弟を追いかけた。
弟は50m/分、兄は70m/分だったとき、兄は家を出て何分後に弟に追いつくか求めよ
この動画を見る
弟が5km離れた学校に向かって家を出た。
弟の忘れ物に気づいた兄は、その8分後に家を出て、弟を追いかけた。
弟は50m/分、兄は70m/分だったとき、兄は家を出て何分後に弟に追いつくか求めよ
【中学理科】植物の具体例の語呂合わせ~シダ植物・種子植物~【中1理科】

割と意味わからんくない?

これどう?

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$(x+a)^2=x^2+2ax+a^2$
図で説明してください
この動画を見る
$(x+a)^2=x^2+2ax+a^2$
図で説明してください
元素記号こう覚えましたか?

高校生が今すぐするべき勉強とは?~ここみらい×あきとんとん~

これの説明できる?

自然数ってなんですか?

これ問題不成立なんですか?

因数分解や解の公式が不要な新しい解き方~2次関数・2次方程式~

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\displaystyle
(1)\,x^2-2x-24=0
$
$\displaystyle
(2)\,3x^2-7x-6=0
$
この動画を見る
$\displaystyle
(1)\,x^2-2x-24=0
$
$\displaystyle
(2)\,3x^2-7x-6=0
$
1=5として,これ解けますか?

単元:
#数学(中学生)#中1数学#中2数学#中3数学#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1=5として
2=25
3=325
4=4325
5=?
この動画を見る
1=5として
2=25
3=325
4=4325
5=?
【中学数学】乗法をどこよりも分かりやすく~累乗と指数~ 1-5【中1数学】

単元:
#数学(中学生)#中1数学#正の数・負の数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\displaystyle
(1)\,(+8)\times (+3)
$
$\displaystyle
(2)\,(-12)\times (+4)
$
$\displaystyle
(3)\,(-2)\times (-1)\times (+6)\times (-3)
$
$\displaystyle
(4)\,(-3)\times (+\frac{3}{2})
$
$\displaystyle
(5)\,(-3)\times (-\frac{2}{3})\times (+4)
$
$\displaystyle
(6)\,(-\frac{3}{2})\times (+\frac{2}{6})\times(-\frac{2}{5})\times(-\frac{10}{3})
$
$\displaystyle
(7)\,(-0.5)\times (+3)
$
$\displaystyle
(8)\,(-0.2)\times (+2)\times (-\frac{3}{2})
$
この動画を見る
$\displaystyle
(1)\,(+8)\times (+3)
$
$\displaystyle
(2)\,(-12)\times (+4)
$
$\displaystyle
(3)\,(-2)\times (-1)\times (+6)\times (-3)
$
$\displaystyle
(4)\,(-3)\times (+\frac{3}{2})
$
$\displaystyle
(5)\,(-3)\times (-\frac{2}{3})\times (+4)
$
$\displaystyle
(6)\,(-\frac{3}{2})\times (+\frac{2}{6})\times(-\frac{2}{5})\times(-\frac{10}{3})
$
$\displaystyle
(7)\,(-0.5)\times (+3)
$
$\displaystyle
(8)\,(-0.2)\times (+2)\times (-\frac{3}{2})
$
ポケモンで一番強いのって誰ですか?

単元:
#理科(中学受験)#物理#物理分野#熱・波・音#理科(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
熱の伝わり方
・熱伝導
・熱伝達
・輻射
輻射の説明動画です
この動画を見る
熱の伝わり方
・熱伝導
・熱伝達
・輻射
輻射の説明動画です
これ解ける?
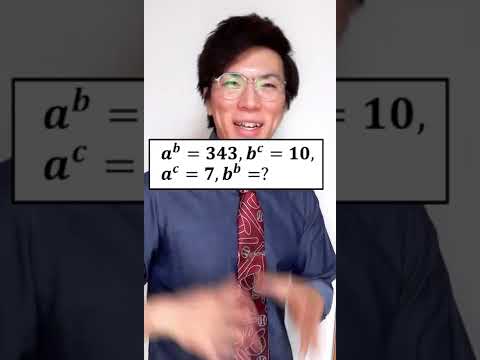
ここ分からんかったやろ?

単元:
#数学(中学生)#中1数学#数Ⅰ#資料の活用#データの分析#データの分析#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
四分位数
四分位範囲
箱ひげ図
解説動画です
この動画を見る
四分位数
四分位範囲
箱ひげ図
解説動画です
こんなに飲めない...

単元:
#算数(中学受験)#文章題#文章題その他
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
ジュースの空き缶5本集めると、新品のジュース1本と交換してもらえる。
あなたは新品のジュースを200本もっている。
何本のジュースが飲めますか?
この動画を見る
ジュースの空き缶5本集めると、新品のジュース1本と交換してもらえる。
あなたは新品のジュースを200本もっている。
何本のジュースが飲めますか?
【中学理科】1本の動画で中1生物分野を全部解説~初学者でも分かる~

このイメージある?

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$(x+a)^2=x^2+2ax+a^2$
図で説明してください
この動画を見る
$(x+a)^2=x^2+2ax+a^2$
図で説明してください
なんでか分かる?

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$7 \times 11 \times 13 $…の計算の謎紹介動画です
この動画を見る
$7 \times 11 \times 13 $…の計算の謎紹介動画です
【中学数学】加法・減法の混じった計算~項とは~ 1-4【中1数学】

単元:
#数学(中学生)#中1数学#正の数・負の数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
次の式の項を求めよ
$\displaystyle
(1)\,-20+50-2+7 \quad(2)\,3-5+5.4-8
$
次の計算をしなさい
$\displaystyle
(1)\,(-3)+(+2)-(-7)\quad(2)\,(+6)+(-3)-(+20)-(-2)\quad(3)\,(+12)-(-5)+(+2)+(-6)
$
この動画を見る
次の式の項を求めよ
$\displaystyle
(1)\,-20+50-2+7 \quad(2)\,3-5+5.4-8
$
次の計算をしなさい
$\displaystyle
(1)\,(-3)+(+2)-(-7)\quad(2)\,(+6)+(-3)-(+20)-(-2)\quad(3)\,(+12)-(-5)+(+2)+(-6)
$
【中学数学】式の値~問題演習で解き方を教えます~ 1-2【中2数学】

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1) $a=5,~b=-8$のとき、$4(2a-7b)-5(a-5b)$を求めよ
(2) $a=6,~b=-7$のとき、$5a^3b^2\div 15a^2b^4\times 2ab^3$を求めよ
(3) $x=\frac{3}{2},~y=-\frac{2}{17}$のとき、$(8x+3y)-2(3x-7y+1)$を求めよ
この動画を見る
(1) $a=5,~b=-8$のとき、$4(2a-7b)-5(a-5b)$を求めよ
(2) $a=6,~b=-7$のとき、$5a^3b^2\div 15a^2b^4\times 2ab^3$を求めよ
(3) $x=\frac{3}{2},~y=-\frac{2}{17}$のとき、$(8x+3y)-2(3x-7y+1)$を求めよ
これの説明できますか?





