 福田次郎
福田次郎
 福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田のおもしろ数学413〜2024個の分数からk個選んできて積を作って合計しよう

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\dfrac{1}{2},\dfrac{1}{3},\dfrac{1}{4},\dfrac{1}{5},\cdots \dfrac{1}{2025}$の$2024$個の数から
異なる$k$個を選んで作った積の総和を$s(k)$とする。
$s(2)+s(4)+s(6)+\cdots +s(2024)$
の値を求めて下さい。
この動画を見る
$\dfrac{1}{2},\dfrac{1}{3},\dfrac{1}{4},\dfrac{1}{5},\cdots \dfrac{1}{2025}$の$2024$個の数から
異なる$k$個を選んで作った積の総和を$s(k)$とする。
$s(2)+s(4)+s(6)+\cdots +s(2024)$
の値を求めて下さい。
福田のおもしろ数学412〜正n角形の内部の点から各辺に下ろした垂線の長さに関する不等式の証明
単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
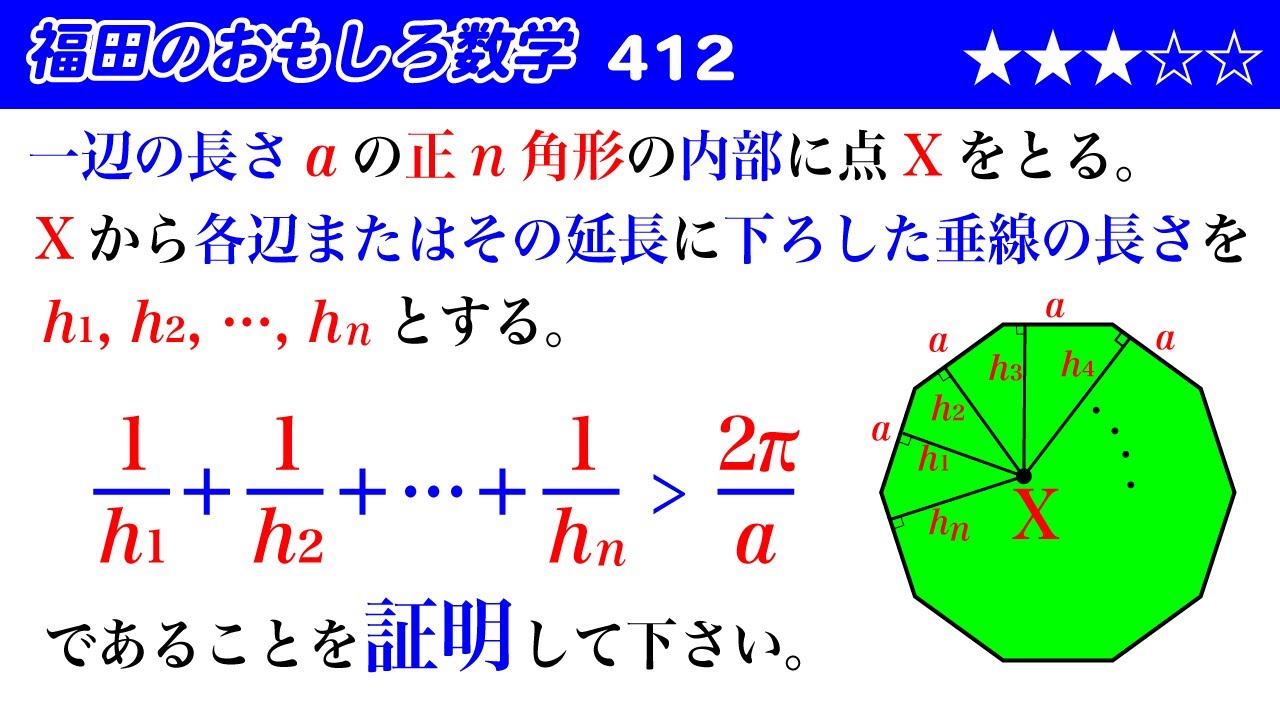
一辺の長さ$a$の正$n$角形の内部に点$X$をとる。
$X$から各辺またはその延長に下ろした垂線の長さを
$h_1,h_2,\cdots h_n$とする。
$\dfrac{1}{h_1}+\dfrac{1}{h_2}+\cdots +\dfrac{1}{h_n} \gt \dfrac{2\pi}{a}$
であることを証明して下さい。
図は動画内参照
この動画を見る
一辺の長さ$a$の正$n$角形の内部に点$X$をとる。
$X$から各辺またはその延長に下ろした垂線の長さを
$h_1,h_2,\cdots h_n$とする。
$\dfrac{1}{h_1}+\dfrac{1}{h_2}+\cdots +\dfrac{1}{h_n} \gt \dfrac{2\pi}{a}$
であることを証明して下さい。
図は動画内参照
福田のおもしろ数学411〜漸化式で定まる数列の2020項までの和と2030項までの和から2025項までの和を求める

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数列$\{a_n\}$は$a_n=a_{n-1}-a_{n-2} (n\geqq 3)$を
満たしている。
$\displaystyle \sum_{n=1}^{2020}=2030$ $\quad $ $\displaystyle \sum_{n=1}^{2030}=2020$
を満たすとき
$\displaystyle \sum_{n=1}^{2025} a_n$の値を求めよ。
この動画を見る
数列$\{a_n\}$は$a_n=a_{n-1}-a_{n-2} (n\geqq 3)$を
満たしている。
$\displaystyle \sum_{n=1}^{2020}=2030$ $\quad $ $\displaystyle \sum_{n=1}^{2030}=2020$
を満たすとき
$\displaystyle \sum_{n=1}^{2025} a_n$の値を求めよ。
福田のおもしろ数学410〜条件を満たすKの最大値

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の貢献を満たす実数$k$の最大値は?
「$a+b+c\leqq K$を満たす任意の正の実数
$a,b,c$に対して$abc \leqq K$が成り立つ」
この動画を見る
次の貢献を満たす実数$k$の最大値は?
「$a+b+c\leqq K$を満たす任意の正の実数
$a,b,c$に対して$abc \leqq K$が成り立つ」
福田のおもしろ数学409〜7進法と2025番目の数

単元:
#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
福田次郎
問題文全文(内容文):
$A=\{0,1,2,3,4,5,6\}$
$M=$
$\left\{\dfrac{a_1}{7}+\dfrac{a_2}{7^2}+\dfrac{a_3}{7^3}+\dfrac{a_4}{7^4} \vert a_i \in A,i=1,2,3,4 \right\}$
$M$のすべての要素を降順に並べる。
$2025$番目の要素を求めて下さい。
この動画を見る
$A=\{0,1,2,3,4,5,6\}$
$M=$
$\left\{\dfrac{a_1}{7}+\dfrac{a_2}{7^2}+\dfrac{a_3}{7^3}+\dfrac{a_4}{7^4} \vert a_i \in A,i=1,2,3,4 \right\}$
$M$のすべての要素を降順に並べる。
$2025$番目の要素を求めて下さい。
福田のおもしろ数学408〜変数が素数である連立方程式

単元:
#連立方程式#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
pq=r+1 \\
2(p^2+q^2)=r^2+1
\end{array}
\right.
\end{eqnarray}$
を満たす素数$p,q,r$を求めて下さい。
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
pq=r+1 \\
2(p^2+q^2)=r^2+1
\end{array}
\right.
\end{eqnarray}$
を満たす素数$p,q,r$を求めて下さい。
福田のおもしろ数学407〜a^3+b^3+c^3-3abcの取り得る最小の正の値

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
正の整数$a,b,c$に対して
$a^3+b^3+c^3-3abc$
が取り得る最小の正の値を求めよ。
またそのときの$a,b,c$の値は?
この動画を見る
正の整数$a,b,c$に対して
$a^3+b^3+c^3-3abc$
が取り得る最小の正の値を求めよ。
またそのときの$a,b,c$の値は?
福田のおもしろ数学406〜2次曲線のグラフを判定する

単元:
#平面上の曲線#2次曲線#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\dfrac{x^2}{\sin\sqrt 2-\sin\sqrt 3}+\dfrac{y^2}{\cos\sqrt2-\cos\sqrt3}=1$
この方程式の表す図形の概形を描け。
この動画を見る
$\dfrac{x^2}{\sin\sqrt 2-\sin\sqrt 3}+\dfrac{y^2}{\cos\sqrt2-\cos\sqrt3}=1$
この方程式の表す図形の概形を描け。
福田のおもしろ数学405〜√2+√3が円周率πよりも大きいことの証明

福田のおもしろ数学404〜単位円に内接する三角形に関する三角関数の値
単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
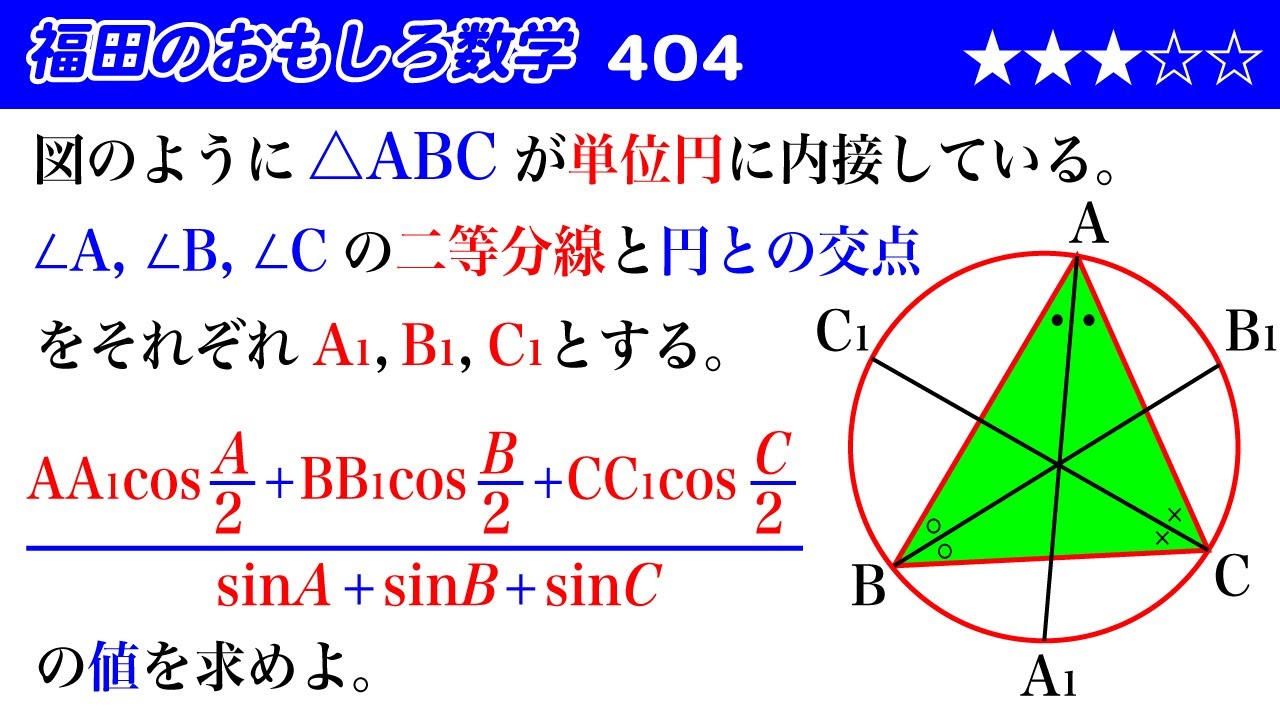
図のように$\triangle ABC$が単位円に内接している。
$\angle A,\angle B,\angle C$の二等分線と円との交点
をそれぞれ$A_1,B_1,C_1$とする。
$\dfrac{AA_1 \cos \dfrac{A}{2}+BB_1\cos\dfrac{B}{2}+CC_1\cos\dfrac{C}{2}}{\sin A+\sin B+\sin C}$
の値を求めよ。
この動画を見る
図のように$\triangle ABC$が単位円に内接している。
$\angle A,\angle B,\angle C$の二等分線と円との交点
をそれぞれ$A_1,B_1,C_1$とする。
$\dfrac{AA_1 \cos \dfrac{A}{2}+BB_1\cos\dfrac{B}{2}+CC_1\cos\dfrac{C}{2}}{\sin A+\sin B+\sin C}$
の値を求めよ。
福田のおもしろ数学403〜条件付きの不等式の証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x+y=2,x\gt 0,y\gt 0$のとき、
$x^3y^3(x^3+y^3)\leqq 2$
を証明して下さい。
この動画を見る
$x+y=2,x\gt 0,y\gt 0$のとき、
$x^3y^3(x^3+y^3)\leqq 2$
を証明して下さい。
福田のおもしろ数学402〜1組の色の揃った手袋を選ぶためには何個取り出せばよいだろうか

単元:
#文章題#文章題その他
指導講師:
福田次郎
問題文全文(内容文):
箱の中に、赤の手袋が5組、緑の手袋が3組、
黄色の手袋が2組、計20の手袋が入っている。
暗闇の中でいくつか選び、
どれを選んだかは後で確認するしかない。
少なくとも1組の色の揃った手袋を手に入れることを
保証するには
最低いくつの手袋を選べばよいだろうか?
この動画を見る
箱の中に、赤の手袋が5組、緑の手袋が3組、
黄色の手袋が2組、計20の手袋が入っている。
暗闇の中でいくつか選び、
どれを選んだかは後で確認するしかない。
少なくとも1組の色の揃った手袋を手に入れることを
保証するには
最低いくつの手袋を選べばよいだろうか?
福田のおもしろ数学401〜極限関数の個数

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=\displaystyle \lim_{n\to\infty} \dfrac{\tan^{2n+1}x-\tan^n x+1}{\tan^{2n+2}x+\tan^{2n}x+1}$
$\left(0\leqq x \lt \dfrac{\pi}{2}\right)$のグラフを描いて下さい。
この動画を見る
$f(x)=\displaystyle \lim_{n\to\infty} \dfrac{\tan^{2n+1}x-\tan^n x+1}{\tan^{2n+2}x+\tan^{2n}x+1}$
$\left(0\leqq x \lt \dfrac{\pi}{2}\right)$のグラフを描いて下さい。
福田のおもしろ数学400〜2項展開の係数と次数に関する個数

単元:
#数Ⅰ#数A#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\left(\sqrt x+\dfrac{1}{2\sqrt[4]{x}}\right)^n$の展開式を降順に並べたとき、
最初の3項の$x$の係数が等差数列になった。
この展開式の中に$x$の次数が整数となる
項は何個あるか?
この動画を見る
$\left(\sqrt x+\dfrac{1}{2\sqrt[4]{x}}\right)^n$の展開式を降順に並べたとき、
最初の3項の$x$の係数が等差数列になった。
この展開式の中に$x$の次数が整数となる
項は何個あるか?
福田のおもしろ数学399〜20002000以下で0と2以外の数字を使わない正の整数の個数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$20002000$以下で$0$と$2$以外の数字を
含まない正の整数は何個あるか?
この動画を見る
$20002000$以下で$0$と$2$以外の数字を
含まない正の整数は何個あるか?
福田のおもしろ数学398〜ガウス記号が付いた1次方程式の解を分類する

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$[x]=ax+1$
を解いて下さい。
*$a$は整数とし、
$[x]$は$x$を超えない最大の整数を表す。
この動画を見る
$[x]=ax+1$
を解いて下さい。
*$a$は整数とし、
$[x]$は$x$を超えない最大の整数を表す。
福田のおもしろ数学397〜与えられた連分数が整数になれないことの証明
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
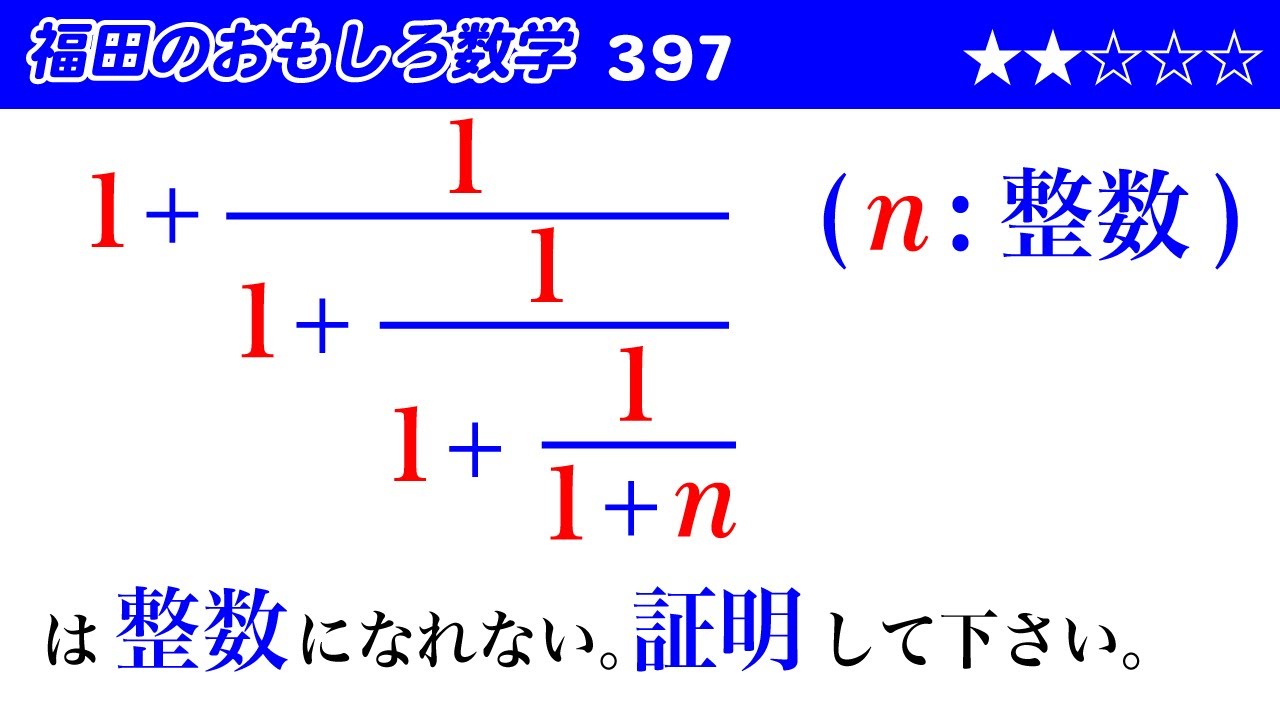
$\begin{eqnarray}
1+\frac{1}{1+\frac{1}{1+\frac{1}{1+n}}}
\end{eqnarray}$
は整数になれない。証明して下さい。
*$n$は整数である。
この動画を見る
$\begin{eqnarray}
1+\frac{1}{1+\frac{1}{1+\frac{1}{1+n}}}
\end{eqnarray}$
は整数になれない。証明して下さい。
*$n$は整数である。
福田のおもしろ数学396〜和が0のn個の実数に対して隣接2項の積の総和が0以下となるnは

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$n\geqq 3$のとき、
$a_1+a_2+\cdots+a_n=0$を
満たすすべての実数$a_1,a_2\cdots a_n$について
$a_1a_2+a_2a_3+\cdots+a_{n-1}a_n+a_na_1 \leqq 0$
が成り立つような整数$n$をすべて求めよ。
この動画を見る
$n\geqq 3$のとき、
$a_1+a_2+\cdots+a_n=0$を
満たすすべての実数$a_1,a_2\cdots a_n$について
$a_1a_2+a_2a_3+\cdots+a_{n-1}a_n+a_na_1 \leqq 0$
が成り立つような整数$n$をすべて求めよ。
福田のおもしろ数学395〜2変数関数の最大値

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$x\gt 0,y\gt 0$のとき、
$f(x,y=min \left(x,\dfrac{y}{x^2+y^2}\right)$
の最大値を求めて下さい。
*$min(a,b)$は$a,b$の大きくない方の値を
意味します。
この動画を見る
$x\gt 0,y\gt 0$のとき、
$f(x,y=min \left(x,\dfrac{y}{x^2+y^2}\right)$
の最大値を求めて下さい。
*$min(a,b)$は$a,b$の大きくない方の値を
意味します。
福田のおもしろ数学394〜6次の多項式に関する証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
6次の多項式$P(x)$について
$0\lt a \lt b$が
$P(a)=P(-a),P(b)=P(-b),P'(0)=0$
を満たしている。
任意の$x$に対し$P(x)=P(-x)$が
成り立つことを証明せよ。
この動画を見る
6次の多項式$P(x)$について
$0\lt a \lt b$が
$P(a)=P(-a),P(b)=P(-b),P'(0)=0$
を満たしている。
任意の$x$に対し$P(x)=P(-x)$が
成り立つことを証明せよ。
福田のおもしろ数学393〜半径1の円板上の点を3つに分類して距離1離れた2点が同じ部分集合に属さないようにできるか

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
半径1の円板(周も含む)上の点を3つの部分集合に分割し、
それぞれの部分集合において、
距離が1離れた2点を含まないようにすることは可能か?
この動画を見る
半径1の円板(周も含む)上の点を3つの部分集合に分割し、
それぞれの部分集合において、
距離が1離れた2点を含まないようにすることは可能か?
福田のおもしろ数学392〜2変数関数についての関数方程式

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
任意の正の整数$x,y$に対して定義された関数$f$は
$f(x,x)=x,f(x,y)=f(y,x)(x+y)f(x,y)=$
$yf(x,x+y)$
を満たしている。
このような関数$f(x,y)$をすべて求めよ。
この動画を見る
任意の正の整数$x,y$に対して定義された関数$f$は
$f(x,x)=x,f(x,y)=f(y,x)(x+y)f(x,y)=$
$yf(x,x+y)$
を満たしている。
このような関数$f(x,y)$をすべて求めよ。
福田のおもしろ数学391〜簡単な関数方程式

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
任意の実数$x,y$に対して$f(0)=1$、
$f(xy+1)=f(x)f(y)-f(y)-x+2$
が成り立つような実数値関数$f(x)$をすべて求めて下さい。
この動画を見る
任意の実数$x,y$に対して$f(0)=1$、
$f(xy+1)=f(x)f(y)-f(y)-x+2$
が成り立つような実数値関数$f(x)$をすべて求めて下さい。
福田のおもしろ数学390〜対数の性質

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a,b,c,d$は正の整数である。
$\log_a b=\dfrac{3}{2},\log_c d=\dfrac{5}{4},a-c=9$のとき、
$b-d$はいくつであるか?
この動画を見る
$a,b,c,d$は正の整数である。
$\log_a b=\dfrac{3}{2},\log_c d=\dfrac{5}{4},a-c=9$のとき、
$b-d$はいくつであるか?
福田のおもしろ数学389〜三角関数を含んだ連立方程式

単元:
#数学(中学生)#中2数学#連立方程式#三角関数
指導講師:
福田次郎
問題文全文(内容文):
連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
\sin x = y \\
\sin y = x
\end{array}
\right.
\end{eqnarray}$
を解いて下さい。
この動画を見る
連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
\sin x = y \\
\sin y = x
\end{array}
\right.
\end{eqnarray}$
を解いて下さい。
福田のおもしろ数学388〜条件付き最小問題

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
正の実数$x,y,z$が次を満たしている。
$x\sqrt{yz}+y\sqrt{zx}+z\sqrt{xy} \geqq 1$
このとき、$x+y+z$の最小値を求めよ。
この動画を見る
正の実数$x,y,z$が次を満たしている。
$x\sqrt{yz}+y\sqrt{zx}+z\sqrt{xy} \geqq 1$
このとき、$x+y+z$の最小値を求めよ。
福田のおもしろ数学387〜連立方程式を解こう

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
福田次郎
問題文全文(内容文):
$x,y,z$は正の実数とする。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x - y + \dfrac{1}{z}=2025 \\
y - z + \dfrac{1}{x}=2025 \\\
z - x + \dfrac{1}{y}=2025
\end{array}
\right.
\end{eqnarray}$
を解いて下さい。
この動画を見る
$x,y,z$は正の実数とする。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x - y + \dfrac{1}{z}=2025 \\
y - z + \dfrac{1}{x}=2025 \\\
z - x + \dfrac{1}{y}=2025
\end{array}
\right.
\end{eqnarray}$
を解いて下さい。
福田のおもしろ数学386〜ルートの付いた不定方程式の解

単元:
#整数の性質#約数・倍数・整数の割り算と余り・合同式
指導講師:
福田次郎
問題文全文(内容文):
a,b,cは0以上の整数
\begin{equation}
\sqrt{a}+\sqrt{b}+\sqrt{c}=\sqrt{2026}
\end{equation}
を満たす(a,b,c)の組をすべて求めよ。
この動画を見る
a,b,cは0以上の整数
\begin{equation}
\sqrt{a}+\sqrt{b}+\sqrt{c}=\sqrt{2026}
\end{equation}
を満たす(a,b,c)の組をすべて求めよ。
福田の数学〜過去の入試問題(期間限定)〜千葉大学理系2020第1問〜確率の基本性質

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
Aさんは1が書かれたカードを1枚、2が書かれたカードを2枚、4が書かれたカードを1枚、計4枚を無作為に横一列に並べて4桁の数Xを作る。Bさんは2が書かれたカードを2枚、3が書かれたカードを2枚、計4枚を無作為に横一列に並べて4桁の数Yを作る。
$$(1)Xが4の倍数となる確率を求めよ。
(2)X \lt Yとなる確率を求めよ。$$
この動画を見る
Aさんは1が書かれたカードを1枚、2が書かれたカードを2枚、4が書かれたカードを1枚、計4枚を無作為に横一列に並べて4桁の数Xを作る。Bさんは2が書かれたカードを2枚、3が書かれたカードを2枚、計4枚を無作為に横一列に並べて4桁の数Yを作る。
$$(1)Xが4の倍数となる確率を求めよ。
(2)X \lt Yとなる確率を求めよ。$$
福田のおもしろ数学385〜1^2025+2^2025+…+2024^2025を45で割った余り

単元:
#数A#整数の性質#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$1^{2025}+2^{2025}+…+2024^{2025}$
を$45$で割った余り
を求めてください。
この動画を見る
$1^{2025}+2^{2025}+…+2024^{2025}$
を$45$で割った余り
を求めてください。



