福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田の数学〜神戸大学2025理系第4問〜空間ベクトルと三角形の面積の最小
単元：
#数A#大学入試過去問(数学)#図形の性質#空間ベクトル#三角形の辺の比（内分・外分・二等分線）#空間ベクトル#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
$s,t$を実数とする。座標空間に$3$点
$A(-4,-1,0),B(-3,0,-1),P(s,t,-2s+t-1)$がある。
以下の問いに答えよ。
(1)$3$点$A,B,P$は一直線上にないことを示せ。
(2)点$P$から直線$AB$に下ろした垂線を$PH$とする。
点$H$の座標を$s$を用いて表せ。
(3)$s,t$が変化するとき、
三角形$ABP$の面積の最小値を求めよ。
$2025$年神戸大学理系過去問題
この動画を見る
$\boxed{4}$
$s,t$を実数とする。座標空間に$3$点
$A(-4,-1,0),B(-3,0,-1),P(s,t,-2s+t-1)$がある。
以下の問いに答えよ。
(1)$3$点$A,B,P$は一直線上にないことを示せ。
(2)点$P$から直線$AB$に下ろした垂線を$PH$とする。
点$H$の座標を$s$を用いて表せ。
(3)$s,t$が変化するとき、
三角形$ABP$の面積の最小値を求めよ。
$2025$年神戸大学理系過去問題
福田のおもしろ数学535〜1分チャレンジ！分数の計算
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\dfrac{20262025^2}{20262024^2+20262026^2-2}$
を計算して下さい。
この動画を見る
$\dfrac{20262025^2}{20262024^2+20262026^2-2}$
を計算して下さい。
福田の数学〜神戸大学2025理系第3問〜媒介変数表示で表された曲線
単元：
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#微分法と積分法#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#神戸大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
媒介変数$\theta$を用いて
$x=\sin\theta,y=\cos\theta + \vert \sin\theta \vert \quad (0\leqq \theta \leqq 2\pi)$
で表される曲線を$C$とする。以下の問いに答えよ。
(1)曲線$C$の概形をかけ。
(2)曲線$C$で囲まれた部分の面積を求めよ。
$2025$年神戸大学理系過去問題
この動画を見る
$\boxed{3}$
媒介変数$\theta$を用いて
$x=\sin\theta,y=\cos\theta + \vert \sin\theta \vert \quad (0\leqq \theta \leqq 2\pi)$
で表される曲線を$C$とする。以下の問いに答えよ。
(1)曲線$C$の概形をかけ。
(2)曲線$C$で囲まれた部分の面積を求めよ。
$2025$年神戸大学理系過去問題
福田のおもしろ数学534〜不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a,b$が正の実数のとき
$\sqrt[3]{\dfrac{a}{b}}+\sqrt[3]{{b}{a}}\leqq \sqrt[3]{2(a+b)\left(\dfrac{1}{a}+\dfrac{1}{b}\right)}$
を証明して下さい。
この動画を見る
$a,b$が正の実数のとき
$\sqrt[3]{\dfrac{a}{b}}+\sqrt[3]{{b}{a}}\leqq \sqrt[3]{2(a+b)\left(\dfrac{1}{a}+\dfrac{1}{b}\right)}$
を証明して下さい。
福田の数学〜神戸大学2025理系第2問〜整数部分と小数部分
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
実数$a$に対して、$a$を超えない最大の整数を
$k$とするとき、
$a-k$を$a$の小数部分という。
$n$を自然数とし、$a_n=\sqrt{n^2+1}-n$とおく。
以下の問いに答えよ。
(1)$0\lt a_n \lt 1$が成り立つことを示せ。
(2)$b_n$を$\left(3n-\dfrac{1}{a_n}\right)$の小数部分とする。
$b_n$を$n$を用いて表せ。
(3)$b_n$を(2)で定めるものとする。
$m,n$を異なる$2$つの自然数とするとき、
$a_m+b_n \neq 1$であることを示せ。
$2025$年神戸大学理系過去問題
この動画を見る
$\boxed{2}$
実数$a$に対して、$a$を超えない最大の整数を
$k$とするとき、
$a-k$を$a$の小数部分という。
$n$を自然数とし、$a_n=\sqrt{n^2+1}-n$とおく。
以下の問いに答えよ。
(1)$0\lt a_n \lt 1$が成り立つことを示せ。
(2)$b_n$を$\left(3n-\dfrac{1}{a_n}\right)$の小数部分とする。
$b_n$を$n$を用いて表せ。
(3)$b_n$を(2)で定めるものとする。
$m,n$を異なる$2$つの自然数とするとき、
$a_m+b_n \neq 1$であることを示せ。
$2025$年神戸大学理系過去問題
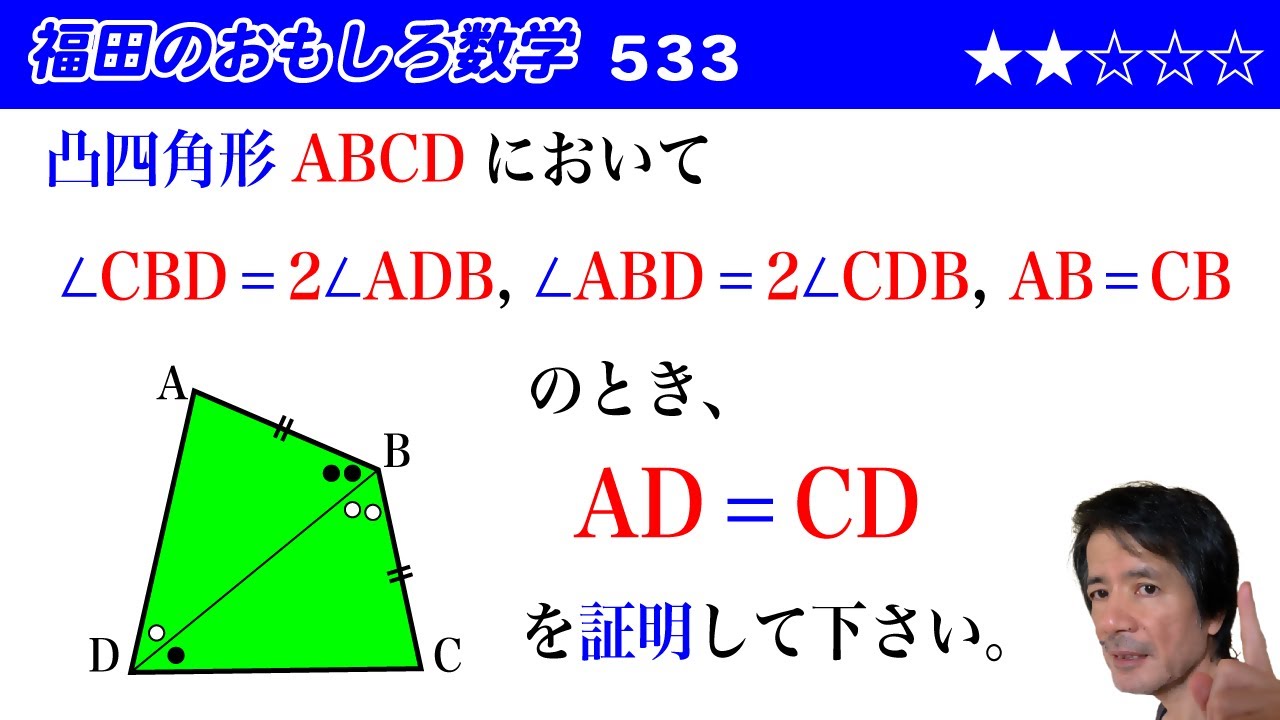
福田のおもしろ数学533〜凸四角形の性質に関する証明
単元：
#数A#数Ⅱ#図形の性質#式と証明#周角と円に内接する四角形・円と接線・接弦定理#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
凸四角形$ABCD$において
$\angle CBD = 2\angle ADB,\angle ABD = 2\angle CDB,AB=CB$
のとき、
$AD=CD$を証明して下さい。
図は動画内参照
この動画を見る
凸四角形$ABCD$において
$\angle CBD = 2\angle ADB,\angle ABD = 2\angle CDB,AB=CB$
のとき、
$AD=CD$を証明して下さい。
図は動画内参照
福田の数学〜神戸大学2025理系第1問〜曲線と直線の共有点の個数
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
$k$を実数とする。
$f(x)$と$g(x)$を
$f(x) = \vert x^3-x \vert,\quad g(x)=k(x+1)$
とおき、曲線$y=f(x)$を$C$、
直線$y=g(x)$を$\ell$とする。以下の問いに答えよ。
(1)曲線$C$の概形をかけ。
ただし、関数$f(x)$の極大値を調べる必要はない。
(2)曲線$C$と直線$\ell$がちょうど$4$つの
共有点をもつような$k$の値を求めよ。
$2025$年神戸大学理系過去問題
この動画を見る
$\boxed{1}$
$k$を実数とする。
$f(x)$と$g(x)$を
$f(x) = \vert x^3-x \vert,\quad g(x)=k(x+1)$
とおき、曲線$y=f(x)$を$C$、
直線$y=g(x)$を$\ell$とする。以下の問いに答えよ。
(1)曲線$C$の概形をかけ。
ただし、関数$f(x)$の極大値を調べる必要はない。
(2)曲線$C$と直線$\ell$がちょうど$4$つの
共有点をもつような$k$の値を求めよ。
$2025$年神戸大学理系過去問題
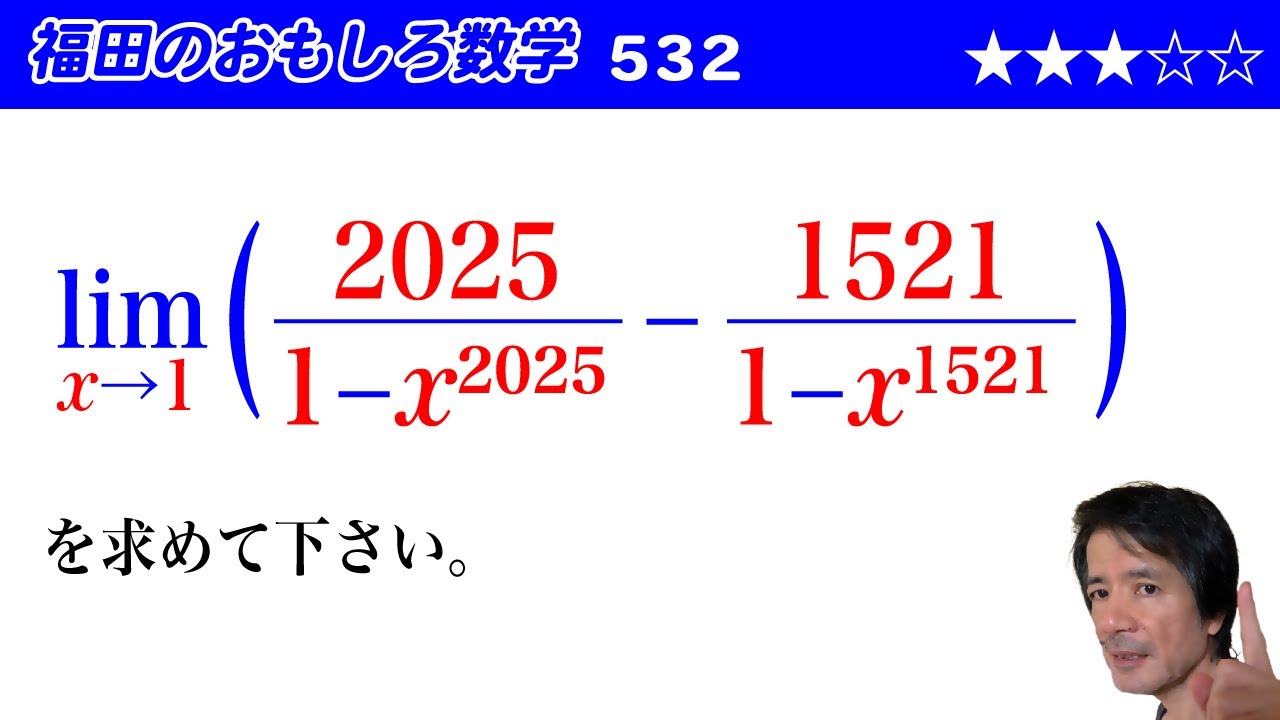
福田のおもしろ数学532〜「∞ー∞」型の極限
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\displaystyle \lim_{x\to 1} \left(\dfrac{2025}{1-x^{2025}}-\dfrac{1521}{1-x^{1521}}\right)$
を求めて下さい。
この動画を見る
$\displaystyle \lim_{x\to 1} \left(\dfrac{2025}{1-x^{2025}}-\dfrac{1521}{1-x^{1521}}\right)$
を求めて下さい。
福田の数学〜大阪大学2025文系第3問〜放物線と接線が作る面積の最大値
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
座標平面において、$y=x^2-1$で表される放物線を
$C$とする。
$C$上の点$P$における$C$の接線を$\ell$とする。
ただし、点$P$は$y$軸上にはないものとする。
$O$を原点とし、放物線$C$と線分$OP$をよび
$y$軸で囲まれた図形の面積を$S$、
放物線$C$と接線$\ell$および$y$軸で囲まれた図形の
面積を$T$とする。
$S-T$の最大値を求めよ。
$2025$年大阪大学文系過去問題
この動画を見る
$\boxed{3}$
座標平面において、$y=x^2-1$で表される放物線を
$C$とする。
$C$上の点$P$における$C$の接線を$\ell$とする。
ただし、点$P$は$y$軸上にはないものとする。
$O$を原点とし、放物線$C$と線分$OP$をよび
$y$軸で囲まれた図形の面積を$S$、
放物線$C$と接線$\ell$および$y$軸で囲まれた図形の
面積を$T$とする。
$S-T$の最大値を求めよ。
$2025$年大阪大学文系過去問題
福田のおもしろ数学531〜三角形に関する命題とその逆
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
左の三角形$ABC$において
$\angle A=3\angle B$
$\Rightarrow (a^2-b^2)(a-b)=bc^2$
が成り立つことを示せ。
また、逆は成り立つか？
図は動画内参照
この動画を見る
左の三角形$ABC$において
$\angle A=3\angle B$
$\Rightarrow (a^2-b^2)(a-b)=bc^2$
が成り立つことを示せ。
また、逆は成り立つか？
図は動画内参照
福田の数学〜大阪大学2025文系第2問〜漸化式と数列の和
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#漸化式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
次の条件によって定められる数列$\{ a_n\}$がある。
$a_1=1,a_{n+1}=\dfrac{2n-1}{2n}a_n \quad (n=1,2,3,\cdots)$
(1)正の整数$k,\ell$に対して
$\dfrac{k}{k+\ell-1}a_{k+1}a_{\ell}+\dfrac{\ell}{k+\ell-1}a_ka_{\ell+1}=a_ka_{\ell}$
が成り立つことを示せ。
(2)正の整数$m$に対して
$\displaystyle \sum_{k=1}^{m} a_ka_{m-K+1}=1$
が成り立つことを示せ。
$2025$年大阪大学文系過去問題
この動画を見る
$\boxed{2}$
次の条件によって定められる数列$\{ a_n\}$がある。
$a_1=1,a_{n+1}=\dfrac{2n-1}{2n}a_n \quad (n=1,2,3,\cdots)$
(1)正の整数$k,\ell$に対して
$\dfrac{k}{k+\ell-1}a_{k+1}a_{\ell}+\dfrac{\ell}{k+\ell-1}a_ka_{\ell+1}=a_ka_{\ell}$
が成り立つことを示せ。
(2)正の整数$m$に対して
$\displaystyle \sum_{k=1}^{m} a_ka_{m-K+1}=1$
が成り立つことを示せ。
$2025$年大阪大学文系過去問題
福田のおもしろ数学530〜三角関数の最大値
単元：
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x_i \in R \ (i=1,2,\cdots,n)$
$n$は$2$以上の自然数
$\sin x_1 \cos x_2 +\sin x_2 \cos x_3+ \cdots + \sin x_n \cos x_1$
の最大値を求めよ。
この動画を見る
$x_i \in R \ (i=1,2,\cdots,n)$
$n$は$2$以上の自然数
$\sin x_1 \cos x_2 +\sin x_2 \cos x_3+ \cdots + \sin x_n \cos x_1$
の最大値を求めよ。
福田の数学〜大阪大学2025理系第5問〜確率漸化式
単元：
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#数列#数列とその和（等差・等比・階差・Σ）#漸化式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{5}$
投げたときに表と裏の出る確率が
それぞれ$\dfrac{1}{2}$のコインがある。
$A,B,C$の$3$文字を$BAC$のように$1$個ずつ
すべて並べて得られる文字列に対して、
コインを投げて次の操作を行う。
・表がで出たら文字列の左から$1$文字目と
$2$文字目を入れかえる。
・裏がで出たら文字列の左から$2$文字目と
$3$文字目を入れかえる。
例えば、文字列が$BAC$であるときに、
$2$回続けてコインを投げて表、裏の順に出た
とすると、文字列は$BAC$から$ABC$を経て
$ACB$となる。
最初の文字列は$ABC$であるとする。
コインを$n$回続けて投げたあとの文字列が
$ABC$である確率を$p_n$とし、
$BCA$である確率を$q_n$とする。
(1)$k$を正の整数とするとき、
$p_{2k}-q_{2k}$を求めよ。
(2)$n$を正の整数とするとき、
$p_n$を求めよ。
$2025$年大阪大学理系過去問題
この動画を見る
$\boxed{5}$
投げたときに表と裏の出る確率が
それぞれ$\dfrac{1}{2}$のコインがある。
$A,B,C$の$3$文字を$BAC$のように$1$個ずつ
すべて並べて得られる文字列に対して、
コインを投げて次の操作を行う。
・表がで出たら文字列の左から$1$文字目と
$2$文字目を入れかえる。
・裏がで出たら文字列の左から$2$文字目と
$3$文字目を入れかえる。
例えば、文字列が$BAC$であるときに、
$2$回続けてコインを投げて表、裏の順に出た
とすると、文字列は$BAC$から$ABC$を経て
$ACB$となる。
最初の文字列は$ABC$であるとする。
コインを$n$回続けて投げたあとの文字列が
$ABC$である確率を$p_n$とし、
$BCA$である確率を$q_n$とする。
(1)$k$を正の整数とするとき、
$p_{2k}-q_{2k}$を求めよ。
(2)$n$を正の整数とするとき、
$p_n$を求めよ。
$2025$年大阪大学理系過去問題
福田の数学〜大阪大学2025理系第4問〜不等式の証明と関数の極限
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
次の問いに答えよ。
(1)$t\gt 0$のとき
$-\dfrac{1}{t}\lt \displaystyle \int_{t}^{2t} \dfrac{\sin x}{x^2}dx \lt \dfrac{1}{t}$
が成り立つことを示せ。
(2)$\displaystyle \lim_{t\to\infty}\displaystyle \dfrac{\cos x}{x}dx=0$を示せ。
(3)$f(x)=\sin\left(\dfrac{3x}{2}\right)\sin\left(\dfrac{x}{2}\right)$おく。
$\displaystyle \lim_{t\to\infty}\displaystyle \int_{1}^{t} \dfrac{f(x)}{x}dx=\dfrac{1}{2} \displaystyle \int_{1}^{2} \dfrac{\cos x}{x} dx$
を示せ。
$2025$年大阪大学理系過去問題
この動画を見る
$\boxed{4}$
次の問いに答えよ。
(1)$t\gt 0$のとき
$-\dfrac{1}{t}\lt \displaystyle \int_{t}^{2t} \dfrac{\sin x}{x^2}dx \lt \dfrac{1}{t}$
が成り立つことを示せ。
(2)$\displaystyle \lim_{t\to\infty}\displaystyle \dfrac{\cos x}{x}dx=0$を示せ。
(3)$f(x)=\sin\left(\dfrac{3x}{2}\right)\sin\left(\dfrac{x}{2}\right)$おく。
$\displaystyle \lim_{t\to\infty}\displaystyle \int_{1}^{t} \dfrac{f(x)}{x}dx=\dfrac{1}{2} \displaystyle \int_{1}^{2} \dfrac{\cos x}{x} dx$
を示せ。
$2025$年大阪大学理系過去問題
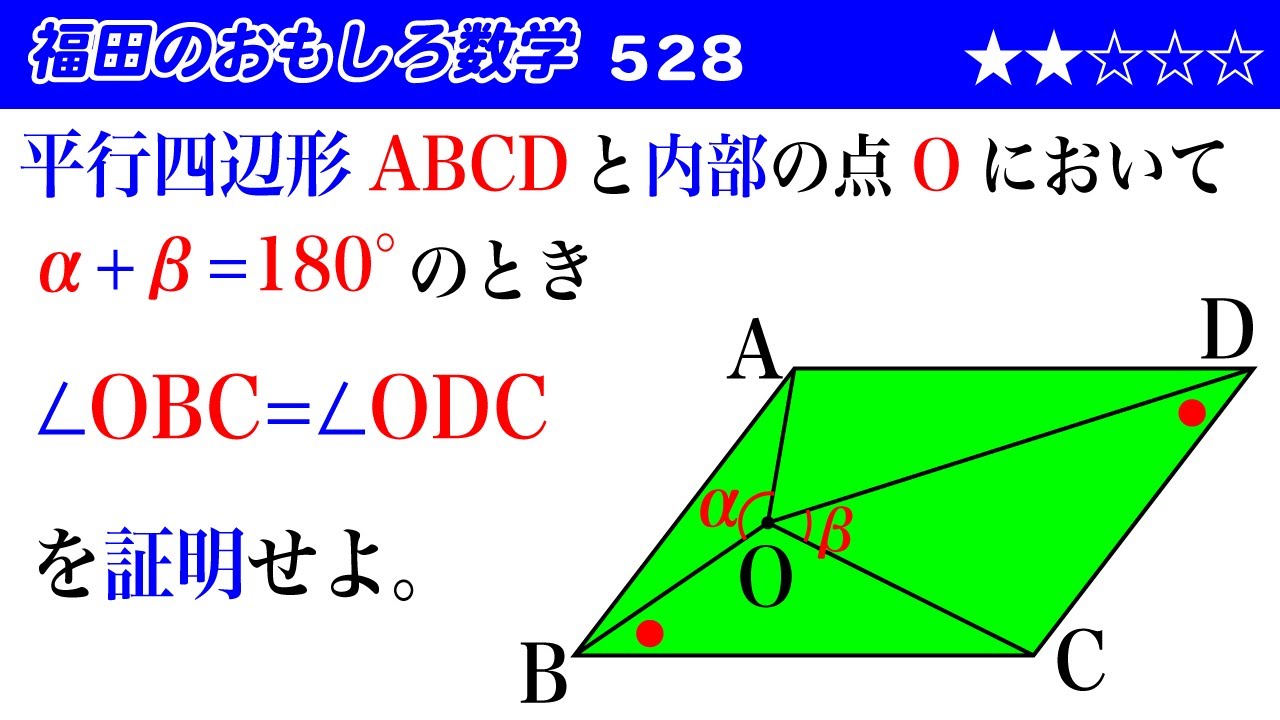
福田のおもしろ数学528〜平面幾何の証明
単元：
#複素数平面#図形への応用#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
平行四辺形$ABCD$と内部の点$O$において
$\alpha+\beta=180°$のとき
$\angle OBC=\angle ODC$
を証明せよ。
図は動画内参照
この動画を見る
平行四辺形$ABCD$と内部の点$O$において
$\alpha+\beta=180°$のとき
$\angle OBC=\angle ODC$
を証明せよ。
図は動画内参照
福田の数学〜大阪大学2025理系第3問〜空間図形と最大最小の軌跡
単元：
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#微分法と積分法#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
座標空間に$3$点$O(0,0,0),A(0,1,1),B(x,y,0)$がある。
$\angle OAP=30°$かつ$y\geqq 0$を満たすように
点$P$が動くとき、
$(x+1)(y+1)$の最大値と最小値を求めよ。
$2025$年大阪大学理系過去問題
この動画を見る
$\boxed{3}$
座標空間に$3$点$O(0,0,0),A(0,1,1),B(x,y,0)$がある。
$\angle OAP=30°$かつ$y\geqq 0$を満たすように
点$P$が動くとき、
$(x+1)(y+1)$の最大値と最小値を求めよ。
$2025$年大阪大学理系過去問題
福田のおもしろ数学527〜最大公約数と最小公倍数からxとyの組の個数を求める
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$gcd(x,y)=5!$
$Icm(x,y)=50!$
$(x\leqq y)$
を満たす自然数の組
$(x,y)$は何組あるか？
この動画を見る
$gcd(x,y)=5!$
$Icm(x,y)=50!$
$(x\leqq y)$
を満たす自然数の組
$(x,y)$は何組あるか？
福田の数学〜大阪大学2025理系第2問〜3次関数の極値と変曲点の軌跡
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
$p$と$m$を実数とし、
関数$f(x)=x^3+3px^2+3mx$は
$x=\alpha$で極大値をとり、
$x=\beta$で極小値をとるとする。
(1)$f(\alpha)-f(\beta)$を$p$と$m$を用いて表せ。
(2)$p$と$m$が$f(\alpha)-f(\beta)=4$を
満たしながら動くとき、
曲線$y=f(x)$の変曲点の軌跡を求めよ。
$2025$年大阪大学理系過去問題
この動画を見る
$\boxed{2}$
$p$と$m$を実数とし、
関数$f(x)=x^3+3px^2+3mx$は
$x=\alpha$で極大値をとり、
$x=\beta$で極小値をとるとする。
(1)$f(\alpha)-f(\beta)$を$p$と$m$を用いて表せ。
(2)$p$と$m$が$f(\alpha)-f(\beta)=4$を
満たしながら動くとき、
曲線$y=f(x)$の変曲点の軌跡を求めよ。
$2025$年大阪大学理系過去問題
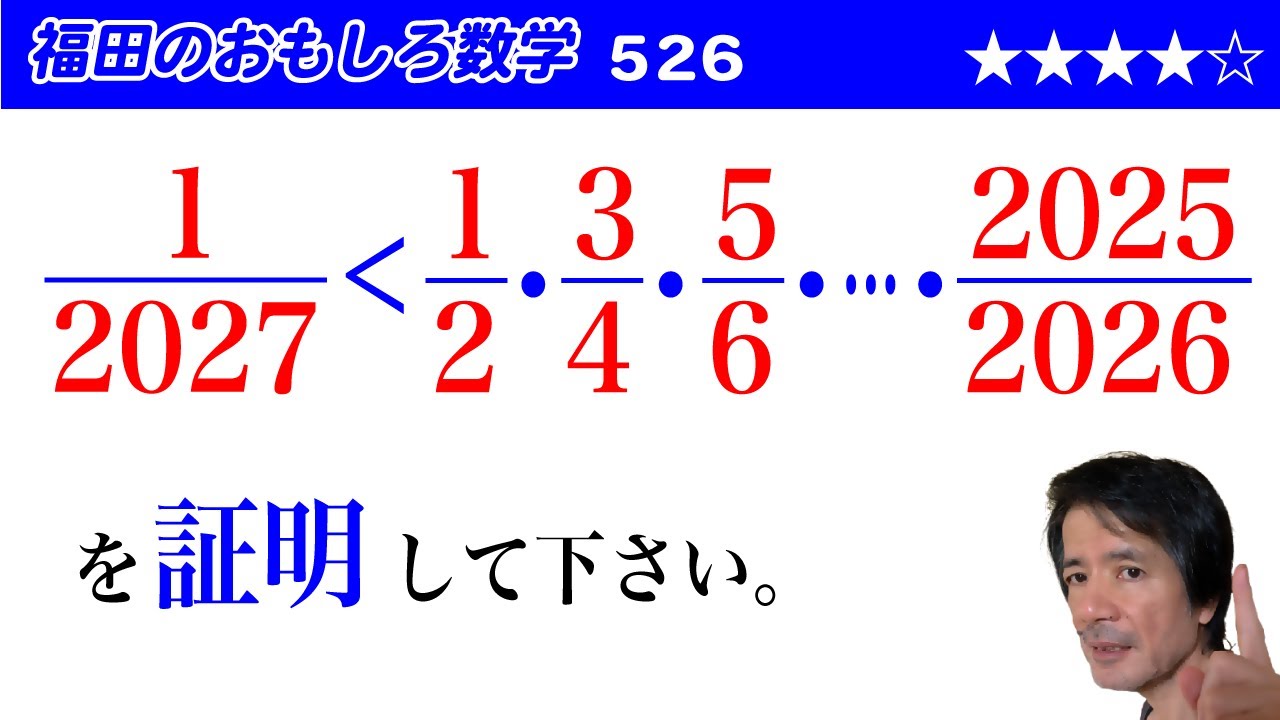
福田のおもしろ数学526〜数値評価
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\dfrac{1}{2027} \lt \dfrac{1}{2}･\dfrac{3}{4}･\dfrac{5}{6}･\cdots ･\dfrac{2025}{2026}$
を証明して下さい。
この動画を見る
$\dfrac{1}{2027} \lt \dfrac{1}{2}･\dfrac{3}{4}･\dfrac{5}{6}･\cdots ･\dfrac{2025}{2026}$
を証明して下さい。
福田の数学〜大阪大学2025理系第1問〜平面図形とベクトルの証明
単元：
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
平面上の三角形$OAB$を考える。
$\angle AOB$は鋭角、$OA=3,OB=t$とする。
また、点$A$から直線$OB$に下ろした垂線と
直線$OB$の交点を$C$とし、$OC=1$とする。
線分$AB$を$2:1$に内分する点を$P$、点$A$から
直線$OP$に下ろした垂線と直線$OB$との交点を
$R$とする。
(1)内積$\overrightarrow{OA}･\overrightarrow{OB}$を$t$を用いて表せ。
(2)線分$OR$の長さを$t$を用いて表せ。
(3)線分$OB$の中点を$M$とする。
点$R$が線分$MB$上にあるとき、
$t$のとりうる値の範囲を求めよ。
$2025$年大阪大学理系過去問題
この動画を見る
$\boxed{1}$
平面上の三角形$OAB$を考える。
$\angle AOB$は鋭角、$OA=3,OB=t$とする。
また、点$A$から直線$OB$に下ろした垂線と
直線$OB$の交点を$C$とし、$OC=1$とする。
線分$AB$を$2:1$に内分する点を$P$、点$A$から
直線$OP$に下ろした垂線と直線$OB$との交点を
$R$とする。
(1)内積$\overrightarrow{OA}･\overrightarrow{OB}$を$t$を用いて表せ。
(2)線分$OR$の長さを$t$を用いて表せ。
(3)線分$OB$の中点を$M$とする。
点$R$が線分$MB$上にあるとき、
$t$のとりうる値の範囲を求めよ。
$2025$年大阪大学理系過去問題
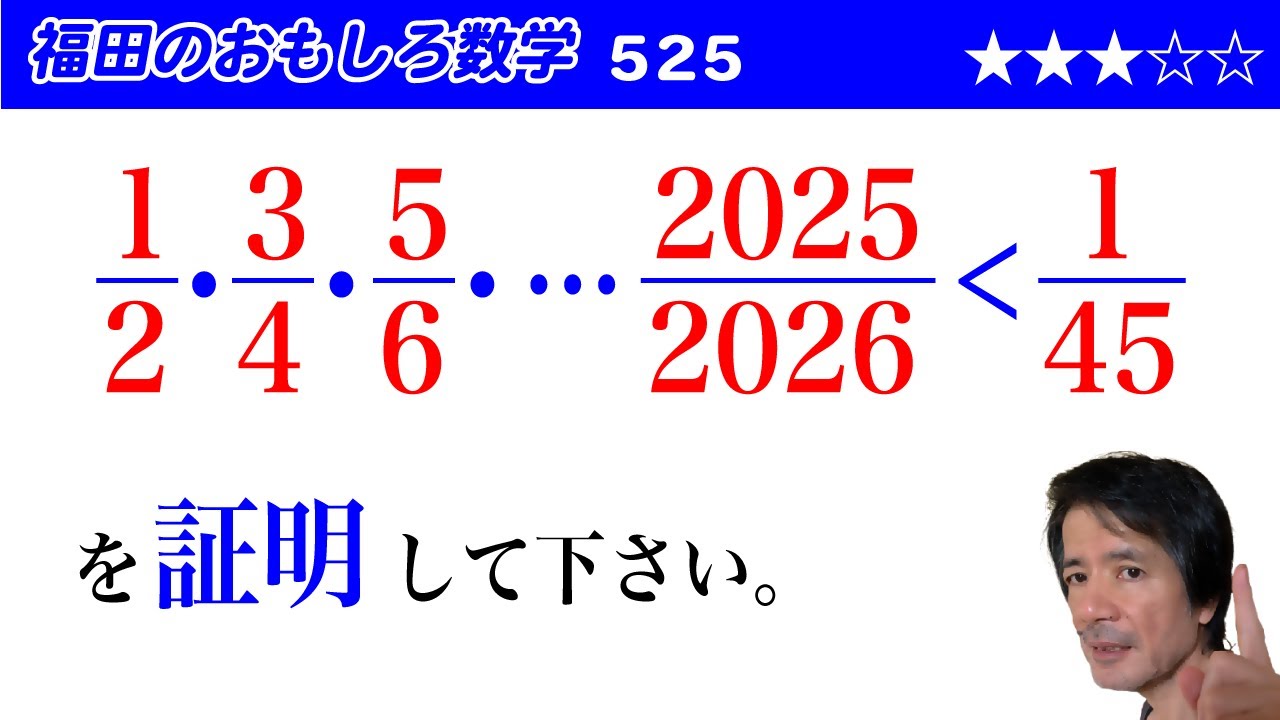
福田のおもしろ数学525〜数値評価
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\dfrac{1}{2}･\dfrac{3}{4}･\dfrac{5}{6}･\cdots \dfrac{2025}{2026}\lt \dfrac{1}{45}$
を証明して下さい。
この動画を見る
$\dfrac{1}{2}･\dfrac{3}{4}･\dfrac{5}{6}･\cdots \dfrac{2025}{2026}\lt \dfrac{1}{45}$
を証明して下さい。
福田の数学〜立教大学2025理学部第4問〜整式がある数の倍数であることの証明
単元：
#数Ⅰ#数A#数と式#式の計算（整式・展開・因数分解）#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数学的帰納法#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
$n$を$2$以上の自然数とする。次の問いに答えよ。
(1)$n^3-n$は$6$のばいすうであることを示せ。
(2)$n^4+2n^3-n^2-2n$は$24$の倍数であることを示せ。
(3)$n$に関する数学的帰納法を用いて、
$n^5+4n$は$5$の倍数であることを示せ。
(4)$n^9+2n^8-n^7-2n^6+4n^5+8n^4-4n^3-8n^2$は
$120$の倍数であることを示せ。
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{4}$
$n$を$2$以上の自然数とする。次の問いに答えよ。
(1)$n^3-n$は$6$のばいすうであることを示せ。
(2)$n^4+2n^3-n^2-2n$は$24$の倍数であることを示せ。
(3)$n$に関する数学的帰納法を用いて、
$n^5+4n$は$5$の倍数であることを示せ。
(4)$n^9+2n^8-n^7-2n^6+4n^5+8n^4-4n^3-8n^2$は
$120$の倍数であることを示せ。
$2025$年立教大学理学部過去問題
福田のおもしろ数学524〜無限級数の和
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\displaystyle \sum_{k=1}^{\infty} \dfrac{k^2}{3^k}$を求めて下さい。
この動画を見る
$\displaystyle \sum_{k=1}^{\infty} \dfrac{k^2}{3^k}$を求めて下さい。
福田の数学〜立教大学2025理学部第3問〜指数関数と円でできる領域の面積
単元：
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
$a,p$は正の実数とする。
座標平面上の曲線$C_1:y=e^x$と$C_1$上の点
$(p,e^p)$がある。
$P$における$C_1$の法線を$\ell,\ell$と$x$軸の
交点を$A(a,0)$、$A$を中心とする半径$r$の円を
$C_2$とする。
$P$が$C_1$と$C_2$のただ一つの共有点であるとき、
次の問いに答えよ。
(1)$\ell$の方程式を$p$を用いて表せ。
(2)$a$を$p$を用いて表せ。
(3)$r$を$p$を用いて表せ。
(4)$\angle OAP=\dfrac{\pi}{6}$のとき、$p$の値を求めよ。
(5)$p$を(4)で求めた値とするとき、
次の不等式の表す領域$D$の面積$S$を求めよ。
$-2 \leqq x \leqq p,\ y\geqq 0,\ y\leqq e^x,$
$(x-a)^2+y^2\geqq r^2$
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{3}$
$a,p$は正の実数とする。
座標平面上の曲線$C_1:y=e^x$と$C_1$上の点
$(p,e^p)$がある。
$P$における$C_1$の法線を$\ell,\ell$と$x$軸の
交点を$A(a,0)$、$A$を中心とする半径$r$の円を
$C_2$とする。
$P$が$C_1$と$C_2$のただ一つの共有点であるとき、
次の問いに答えよ。
(1)$\ell$の方程式を$p$を用いて表せ。
(2)$a$を$p$を用いて表せ。
(3)$r$を$p$を用いて表せ。
(4)$\angle OAP=\dfrac{\pi}{6}$のとき、$p$の値を求めよ。
(5)$p$を(4)で求めた値とするとき、
次の不等式の表す領域$D$の面積$S$を求めよ。
$-2 \leqq x \leqq p,\ y\geqq 0,\ y\leqq e^x,$
$(x-a)^2+y^2\geqq r^2$
$2025$年立教大学理学部過去問題
福田のおもしろ数学523〜命題の真偽の判定
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x+y$と$x+y^2$がともに有理数であるとき
$x$と$y$はともに有理数であると言えるか？
$x+y$と$x+y^2$と$x+y^3$がすべて
有理数であるとき
$x$と$y$はともに有理数であると言えるか？
この動画を見る
$x+y$と$x+y^2$がともに有理数であるとき
$x$と$y$はともに有理数であると言えるか？
$x+y$と$x+y^2$と$x+y^3$がすべて
有理数であるとき
$x$と$y$はともに有理数であると言えるか？
福田の数学〜立教大学2025理学部第2問〜三角関数の最大最小の定番
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
実数$x$に対し、関数$f(x)$を
$f(x)=\sin^3x+\cos^3x+4sin x \cos x$
により定める。
また、$t=\sin x+\cos x$とおく。次の問いに答えよ。
(1)$\sin x \cos x$を$t$を用いて表せ。
(2)$f(x)$を$t$を用いて表せ。
(3)$x$がすべてに実数を動くとき、
$t$のとりうる値の範囲を求めよ。
(4)$x$がすべてに実数を動くとき、
$f(x)$の最大値と最小値をそれぞれ求めよ。
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{2}$
実数$x$に対し、関数$f(x)$を
$f(x)=\sin^3x+\cos^3x+4sin x \cos x$
により定める。
また、$t=\sin x+\cos x$とおく。次の問いに答えよ。
(1)$\sin x \cos x$を$t$を用いて表せ。
(2)$f(x)$を$t$を用いて表せ。
(3)$x$がすべてに実数を動くとき、
$t$のとりうる値の範囲を求めよ。
(4)$x$がすべてに実数を動くとき、
$f(x)$の最大値と最小値をそれぞれ求めよ。
$2025$年立教大学理学部過去問題
福田のおもしろ数学522〜連続関数の性質
単元：
#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
すべての実数で定義された連続関数$f(x)$に対し、
$\dfrac{f(x)}{x} \ (x\neq 0)$
が常に正であるとき、
$f(0)$の値を求めて下さい。
この動画を見る
すべての実数で定義された連続関数$f(x)$に対し、
$\dfrac{f(x)}{x} \ (x\neq 0)$
が常に正であるとき、
$f(0)$の値を求めて下さい。
福田の数学〜立教大学2025理学部第1問(5)〜ド・モアブルの定理と複素数の計算
単元：
#複素数平面#複素数平面#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(5)$i$を虚数単位とする。
実数$a,b$が等式
$\left(\dfrac{1}{\sqrt2}+\dfrac{1}{\sqrt2}i\right)^9+\left(\dfrac{1}{2}+\dfrac{\sqrt3}{2}i\right)^{11}=a+bi$
を満たすとき、$a=\boxed{ク},b=\boxed{ケ}$である。
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{1}$
(5)$i$を虚数単位とする。
実数$a,b$が等式
$\left(\dfrac{1}{\sqrt2}+\dfrac{1}{\sqrt2}i\right)^9+\left(\dfrac{1}{2}+\dfrac{\sqrt3}{2}i\right)^{11}=a+bi$
を満たすとき、$a=\boxed{ク},b=\boxed{ケ}$である。
$2025$年立教大学理学部過去問題
福田のおもしろ数学521〜不定方程式の整数解を求める2つの方法
単元：
#数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x^2+2xy+y=49$
を満たす正の整数の組
$(x,y)$をすべて求めよ。
この動画を見る
$x^2+2xy+y=49$
を満たす正の整数の組
$(x,y)$をすべて求めよ。
福田の数学〜立教大学2025理学部第1問(4)〜確率の基本的な性質
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(4)箱の中に緑色のカードが$5$枚、
黄色のカードが$4$枚、赤色のカードが$3$枚
入っている。
箱から無作為にカードを$3$枚取り出すとき、
$3$枚とも同じ色である確率は$\boxed{オ}$、
$3$枚の色がすべて異なる確率は$\boxed{カ}$、
$2$枚が同じ色であり、かつ、
残りの$1$枚が他の$2$枚と異なる色である確率は
$\boxed{キ}$である。
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{1}$
(4)箱の中に緑色のカードが$5$枚、
黄色のカードが$4$枚、赤色のカードが$3$枚
入っている。
箱から無作為にカードを$3$枚取り出すとき、
$3$枚とも同じ色である確率は$\boxed{オ}$、
$3$枚の色がすべて異なる確率は$\boxed{カ}$、
$2$枚が同じ色であり、かつ、
残りの$1$枚が他の$2$枚と異なる色である確率は
$\boxed{キ}$である。
$2025$年立教大学理学部過去問題