福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田の数学〜早稲田大学理工学部2025第3問〜完全順列と漸化式
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
$1$から$n$までの異なる自然数が$1$つずつ書かれた
$n$枚のカードが一列に並んでいる。
このとき、
どのカードも現在とは異なる位置に移動するよう
並べ替えてできる順列の総数を$a_n$で表し、
並べ方の総数$n!$に閉める$a_n$の割合を$p_n$で表す。
例えば、$a_1=0,p_1=0,a_2=1,p_2=\dfrac{1}{2},$
$a_3=2,p_3=\dfrac{1}{3}$である。
(1)$a_4$の値を求めよ。
(2)$n\geqq 3$のとき、$a_n$を$a_{n-1}$と
$a_{n-2}$を用いて表せ。
(3)$n\geqq 2$のとき、$p_n-p_{n-1}$を
$n$を用いて表せ。
$2025$年早稲田大学理工学部過去問題
この動画を見る
$\boxed{3}$
$1$から$n$までの異なる自然数が$1$つずつ書かれた
$n$枚のカードが一列に並んでいる。
このとき、
どのカードも現在とは異なる位置に移動するよう
並べ替えてできる順列の総数を$a_n$で表し、
並べ方の総数$n!$に閉める$a_n$の割合を$p_n$で表す。
例えば、$a_1=0,p_1=0,a_2=1,p_2=\dfrac{1}{2},$
$a_3=2,p_3=\dfrac{1}{3}$である。
(1)$a_4$の値を求めよ。
(2)$n\geqq 3$のとき、$a_n$を$a_{n-1}$と
$a_{n-2}$を用いて表せ。
(3)$n\geqq 2$のとき、$p_n-p_{n-1}$を
$n$を用いて表せ。
$2025$年早稲田大学理工学部過去問題
福田のおもしろ数学475〜関数方程式の正しい解き方
単元：
#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$0$以上の実数の集合を$R'$とする。
$R'→R'$の関数$f(x)$が任意の$x,y$に対して
$xy(y)+yf(x)=f(x)f(y)(f(x)+f(y))$
を満たしている。
$f(x)$を求めて下さい。
この動画を見る
$0$以上の実数の集合を$R'$とする。
$R'→R'$の関数$f(x)$が任意の$x,y$に対して
$xy(y)+yf(x)=f(x)f(y)(f(x)+f(y))$
を満たしている。
$f(x)$を求めて下さい。
福田の数学〜早稲田大学理工学部2025第2問〜領域に含まれる三角形の面積の最大値
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
$xy$平面上で、
連立不等式
$0\lt x \leqq 1,0\leqq y \leqq \log\dfrac{1}{x}$
で定まる領域と$y$軸の
$y\geqq 0$の部分を合わせた図形を$D$とする。
$D$に含まれる三角形の最大値を求めよ。
$2025$年早稲田大学理工学部過去問題
この動画を見る
$\boxed{2}$
$xy$平面上で、
連立不等式
$0\lt x \leqq 1,0\leqq y \leqq \log\dfrac{1}{x}$
で定まる領域と$y$軸の
$y\geqq 0$の部分を合わせた図形を$D$とする。
$D$に含まれる三角形の最大値を求めよ。
$2025$年早稲田大学理工学部過去問題
福田のおもしろ数学474〜3変数の関係からa+b+cの値を求める
単元：
#連立方程式#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
実数$a,b,c$が次の条件を満たしている。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^2+b^2+c^2=1 \\
a^3+b^3+c^3=1
\end{array}
\right.
\end{eqnarray}$
$a+b+c$の値を求めよ。
この動画を見る
実数$a,b,c$が次の条件を満たしている。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^2+b^2+c^2=1 \\
a^3+b^3+c^3=1
\end{array}
\right.
\end{eqnarray}$
$a+b+c$の値を求めよ。
福田の数学〜早稲田大学理工学部2025第1問〜複素数平面上の点の軌跡と面積
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
複素数平面上で、複素数$z$が円$\vert z \vert=1$の上の点を動くとき、
$w=\left(\dfrac{1+\sqrt2}{2}\right)z+\left(\dfrac{1-\sqrt2}{2}\right)\dfrac{1}{z}$
を満たす点$w$の軌跡を$C$とする。
次の問いに答えよ。
(1)$C$はどのような図形か。複素数平面上に図示せよ。
(2)$C$と円$\left \vert z-\dfrac{2+\sqrt2}{2}\right \vert =\sqrt2$の共有点を求めよ。
(3)$C$で囲まれる領域と$\left \vert z-\dfrac{2+\sqrt2}{2}\right \vert \leqq \sqrt2$の
表す領域の共通部分の面積を求めよ。
$2025$年早稲田大学理工学部過去問題
この動画を見る
$\boxed{1}$
複素数平面上で、複素数$z$が円$\vert z \vert=1$の上の点を動くとき、
$w=\left(\dfrac{1+\sqrt2}{2}\right)z+\left(\dfrac{1-\sqrt2}{2}\right)\dfrac{1}{z}$
を満たす点$w$の軌跡を$C$とする。
次の問いに答えよ。
(1)$C$はどのような図形か。複素数平面上に図示せよ。
(2)$C$と円$\left \vert z-\dfrac{2+\sqrt2}{2}\right \vert =\sqrt2$の共有点を求めよ。
(3)$C$で囲まれる領域と$\left \vert z-\dfrac{2+\sqrt2}{2}\right \vert \leqq \sqrt2$の
表す領域の共通部分の面積を求めよ。
$2025$年早稲田大学理工学部過去問題
福田のおもしろ数学473〜難しい連立方程式を解くための飛び道具
単元：
#連立方程式#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
5\left(x+\dfrac{1}{x}\right)=12\left(y+\dfrac{1}{y}\right)=13\left(z+\dfrac{1}{z}\right) \\
xy+yz+zx=1
\end{array}
\right.
\end{eqnarray}$
を満たす実数$x,y,z$をすべて求めよ。
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
5\left(x+\dfrac{1}{x}\right)=12\left(y+\dfrac{1}{y}\right)=13\left(z+\dfrac{1}{z}\right) \\
xy+yz+zx=1
\end{array}
\right.
\end{eqnarray}$
を満たす実数$x,y,z$をすべて求めよ。
福田の数学〜慶應義塾大学理工学部2025第3問〜確率漸化式
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
点$P, Q$を数直線の原点におき、
$1$個のさいころを投げて
出た目に応じて$P, Q$を動かす。
偶数の目が出たときは$P$を正の向きに$1$だけ動かし、
$5$または$6$の目が出たときは
$Q$を正の向きに$1$だけ動かす。
たとえば、$6$の目が出たときは$P, Q$をともに
正の向きに$1$だけ動かす。
$P$と$Q$の距離が初めて$2$となるまで
さいころを投げ続けることとし、
$P$と$Q$の距離が$2$となったら、
それ以降はさいころを投げない。
$n$回さいころを投げて$P$と$Q$の距離が
$2$となる確率を$p_n$とする。
(1)$P_2 = \boxed{シ}$である。
(2)$n$回さいころを投げて、
$P$が$Q$よりも正の向きに
$1$だけ進んでいる確率を$x_n$、
$P$と$Q$が同じ位置にある確率を$y_n$、
$Q$が$P$よりも正の向きに$1$だけ進んでいる確率を
$z_n$とすると、
$y_{n+1}=\boxed{ス}x_n+\boxed{セ}y_n+\boxed{ソ}z_n$
という関係式が成立する。
また、$x_n=\boxed{タ}z_n$が成り立つ。
ただし、$\boxed{ス}$～$\boxed{タ}$には数を記入すること。
(3)関係式
$z_{n+1}+\alpha y_{n+1}=\beta(z_n+\alpha y_n)$
を満たす定数の組$(\alpha,\beta)$は$\boxed{チ}$と$\boxed{ツ}$の$2$組ある。
(4)$p_n$を$n$を用いて表すと$p_n=\boxed{テ}$となる。
$2025$年慶應義塾大学理工学部過去問題
この動画を見る
$\boxed{3}$
点$P, Q$を数直線の原点におき、
$1$個のさいころを投げて
出た目に応じて$P, Q$を動かす。
偶数の目が出たときは$P$を正の向きに$1$だけ動かし、
$5$または$6$の目が出たときは
$Q$を正の向きに$1$だけ動かす。
たとえば、$6$の目が出たときは$P, Q$をともに
正の向きに$1$だけ動かす。
$P$と$Q$の距離が初めて$2$となるまで
さいころを投げ続けることとし、
$P$と$Q$の距離が$2$となったら、
それ以降はさいころを投げない。
$n$回さいころを投げて$P$と$Q$の距離が
$2$となる確率を$p_n$とする。
(1)$P_2 = \boxed{シ}$である。
(2)$n$回さいころを投げて、
$P$が$Q$よりも正の向きに
$1$だけ進んでいる確率を$x_n$、
$P$と$Q$が同じ位置にある確率を$y_n$、
$Q$が$P$よりも正の向きに$1$だけ進んでいる確率を
$z_n$とすると、
$y_{n+1}=\boxed{ス}x_n+\boxed{セ}y_n+\boxed{ソ}z_n$
という関係式が成立する。
また、$x_n=\boxed{タ}z_n$が成り立つ。
ただし、$\boxed{ス}$～$\boxed{タ}$には数を記入すること。
(3)関係式
$z_{n+1}+\alpha y_{n+1}=\beta(z_n+\alpha y_n)$
を満たす定数の組$(\alpha,\beta)$は$\boxed{チ}$と$\boxed{ツ}$の$2$組ある。
(4)$p_n$を$n$を用いて表すと$p_n=\boxed{テ}$となる。
$2025$年慶應義塾大学理工学部過去問題
福田のおもしろ数学472〜漸化式で与えられた数列の逆数の和
単元：
#数列#数列とその和（等差・等比・階差・Σ）#漸化式#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$a_1=2,a_{n+1}={a_n}^2-a_n+1$のとき
$\dfrac{1}{a_1}+\dfrac{1}{a_2}+\dfrac{1}{a_3}+･･･+\dfrac{1}{a_{2025}}\lt 1$
を証明して下さい。
この動画を見る
$a_1=2,a_{n+1}={a_n}^2-a_n+1$のとき
$\dfrac{1}{a_1}+\dfrac{1}{a_2}+\dfrac{1}{a_3}+･･･+\dfrac{1}{a_{2025}}\lt 1$
を証明して下さい。
福田の数学〜慶應義塾大学理工学部2025第2問〜分数関数の接線とベクトル計算
単元：
#大学入試過去問(数学)#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
座標平面上の点$P(1,1)$と点$Q(1,-1)$および
曲線$C:y=\dfrac{1}{x-4}(x\gt 4)$を考える。
(1)曲線$C$の接線で点$Q$を通るものは存在しないことを
証明しなさい。
(2)曲線$C$の接線で点$P$を通るものを$l$とし、
$C$と$l$の接点を$A$とする。
このとき、$l$の方程式は$y=\boxed{キ}$であり、
点$A$の座標は$\boxed{ク}$である。
また、曲線$C$上の点の点$B$が
$\overrightarrow{PB}･\overrightarrow{PA}+\overrightarrow{PA}･\overrightarrow{AQ}+\overrightarrow{AB}･\overrightarrow{AQ}=-\dfrac{2}{3}$
を満たすとき、点$B$の座標は$\boxed{ケ}$である。
(3)$A,B$を(2)で定めた点とする。
正の数$t$に対し、曲線$C$上の点$R\left(t+4,\dfrac{1}{t}\right)$は
点$A$と異なるものとする。
線分$AR$を$2:1$に内分する点を$S$とし、
線分$BS$を$3:2$に内分する点を$T(u,v)$とするとき、
$u$を$t$の式で表すと$u=\boxed{コ}$である。
また、$uv$の値は$t-\boxed{サ}$のとき最小となる。
$2025$年慶應義塾大学理工学部過去問題
この動画を見る
$\boxed{2}$
座標平面上の点$P(1,1)$と点$Q(1,-1)$および
曲線$C:y=\dfrac{1}{x-4}(x\gt 4)$を考える。
(1)曲線$C$の接線で点$Q$を通るものは存在しないことを
証明しなさい。
(2)曲線$C$の接線で点$P$を通るものを$l$とし、
$C$と$l$の接点を$A$とする。
このとき、$l$の方程式は$y=\boxed{キ}$であり、
点$A$の座標は$\boxed{ク}$である。
また、曲線$C$上の点の点$B$が
$\overrightarrow{PB}･\overrightarrow{PA}+\overrightarrow{PA}･\overrightarrow{AQ}+\overrightarrow{AB}･\overrightarrow{AQ}=-\dfrac{2}{3}$
を満たすとき、点$B$の座標は$\boxed{ケ}$である。
(3)$A,B$を(2)で定めた点とする。
正の数$t$に対し、曲線$C$上の点$R\left(t+4,\dfrac{1}{t}\right)$は
点$A$と異なるものとする。
線分$AR$を$2:1$に内分する点を$S$とし、
線分$BS$を$3:2$に内分する点を$T(u,v)$とするとき、
$u$を$t$の式で表すと$u=\boxed{コ}$である。
また、$uv$の値は$t-\boxed{サ}$のとき最小となる。
$2025$年慶應義塾大学理工学部過去問題
福田のおもしろ数学471〜整数が整数で割りきれる条件
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$n$は正の整数とする。
$2025n+510$は$20n+2$で割り切れる。
このような$n$をすべて求めよ。
この動画を見る
$n$は正の整数とする。
$2025n+510$は$20n+2$で割り切れる。
このような$n$をすべて求めよ。
福田の数学〜慶應義塾大学理工学部2025第1問(3)〜逆関数の微分
単元：
#大学入試過去問(数学)#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(3)$f(x)$を微分可能な関数とし、
$g(x)=x^3+x$とする。
関数$g(x)$は微分可能な逆関数$g^{-1}(x)$をもつ。
定数$t$に対して、関数$t^2x^2-f(g^{-1}(x))$は
$x=t^3+t$で極値をとるとする。
このとき、$f'(t)$を$t$の多項式で表すと$f'(t)=\boxed{オ}$となる。
次に、任意の定数$t$に対して、関数$t^2x^2-f(g^{-1}(x))$は
$x=t^3+t$で極値をとるとする。
このとき、$f(0)=-2$ならば$f(1)=\boxed{カ}$である。
$2025$年慶應義塾大学理工学部過去問題
この動画を見る
$\boxed{1}$
(3)$f(x)$を微分可能な関数とし、
$g(x)=x^3+x$とする。
関数$g(x)$は微分可能な逆関数$g^{-1}(x)$をもつ。
定数$t$に対して、関数$t^2x^2-f(g^{-1}(x))$は
$x=t^3+t$で極値をとるとする。
このとき、$f'(t)$を$t$の多項式で表すと$f'(t)=\boxed{オ}$となる。
次に、任意の定数$t$に対して、関数$t^2x^2-f(g^{-1}(x))$は
$x=t^3+t$で極値をとるとする。
このとき、$f(0)=-2$ならば$f(1)=\boxed{カ}$である。
$2025$年慶應義塾大学理工学部過去問題
福田のおもしろ数学470〜不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$t\geqq \dfrac{1}{2},n$は自然数のとき
$t^{2n} \geqq (t-1)^{2n} + (2t-1)^{2n}$
を証明して下さい。
この動画を見る
$t\geqq \dfrac{1}{2},n$は自然数のとき
$t^{2n} \geqq (t-1)^{2n} + (2t-1)^{2n}$
を証明して下さい。
福田の数学〜慶應義塾大学理工学部2025第1問(2)〜6または8または9で割り切れる数の個数
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(2)$n$を自然数とする。
$1$から$n$までの自然数の中で$6$または$8$または
$9$で割り切れるものの個数を$a_n$で表す。
このとき、$a_{30}=\boxed{ウ}$となる。
また、$a_n=1000$を満たす最大の$n$は$\boxed{エ}$である。
$2025$年慶應義塾大学理工学部過去問題
この動画を見る
$\boxed{1}$
(2)$n$を自然数とする。
$1$から$n$までの自然数の中で$6$または$8$または
$9$で割り切れるものの個数を$a_n$で表す。
このとき、$a_{30}=\boxed{ウ}$となる。
また、$a_n=1000$を満たす最大の$n$は$\boxed{エ}$である。
$2025$年慶應義塾大学理工学部過去問題
福田のおもしろ数学469〜xとyに関する方程式を解く
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
方程式
$x+y+\dfrac{1}{x}+\dfrac{1}{y}+4=2(\sqrt{2x+1}+\sqrt{2y+1})$
を満たす正の数$x,y$をすべて求めよ。
この動画を見る
方程式
$x+y+\dfrac{1}{x}+\dfrac{1}{y}+4=2(\sqrt{2x+1}+\sqrt{2y+1})$
を満たす正の数$x,y$をすべて求めよ。
福田の数学〜慶應義塾大学理工学部2025第1問(1)〜複素数平面上の点の軌跡
単元：
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(1)複素数平面上で、方程式
$\vert z+i \vert = 2 \vert z-\sqrt3 \vert$
を満たす点$z$全体が表す図形は、
中心が$\boxed{ア}$,半径が$\boxed{イ}$である。
$2025$年慶應義塾大学理工学部過去問題
この動画を見る
$\boxed{1}$
(1)複素数平面上で、方程式
$\vert z+i \vert = 2 \vert z-\sqrt3 \vert$
を満たす点$z$全体が表す図形は、
中心が$\boxed{ア}$,半径が$\boxed{イ}$である。
$2025$年慶應義塾大学理工学部過去問題
福田のおもしろ数学468〜4変数の連立方程式
単元：
#連立方程式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
実数$x,y,z,w$の連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + y + z + w =5 \\
xy+yz+zw+wx=4 \\\
xyz+yzw+zwx+wxy3 \\\
xyzw=-1
\end{array}
\right.
\end{eqnarray}$
を解いて下さい。
この動画を見る
実数$x,y,z,w$の連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + y + z + w =5 \\
xy+yz+zw+wx=4 \\\
xyz+yzw+zwx+wxy3 \\\
xyzw=-1
\end{array}
\right.
\end{eqnarray}$
を解いて下さい。
福田の数学〜慶應義塾大学薬学部2025第4問〜確率と期待値と無限級数
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
当たりくじが$3$本入っている$9$本のくじがある。
このくじを無作為に$1$本引き、
当たりくじかどうかを確認してから元に戻す試行を、
当たりくじが出るまで繰り返す。
当たりくじが出たときのみ得点を得ることができ、
$n$回目にの試行で当たりくじが出た場合、
得られる得点は$50n$点とする。
$n$回目に得られる得点の期待値を$E_n$とする。
ただし、$n$は自然数とする。
(1)$5$回目までに当たりくじが出る確率は$\boxed{ノ}$である。
(2)$\dfrac{E_n}{E_{n+1}}=\dfrac{10}{7}$であるとき、$n=\boxed{ハ}$である。
(3)$\displaystyle \lim_{n\to\infty}\dfrac{E_n}{E_{n+1}}$を求めると$\boxed{ヒ}$である。
(4)$\displaystyle \sum_{k=1}^{n}E_k$を$n$の式で表すと$\boxed{フ}$であり、
$\displaystyle \sum_{k=1}^{\infty}E_k$を求めると$\boxed{ヘ}$である。
ただし、$\vert r \vert \lt 1$を満たす実数$r$に対し、
$\displaystyle \lim_{n\to\infty}n \times r^n=0$が
成り立つこととする。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{4}$
当たりくじが$3$本入っている$9$本のくじがある。
このくじを無作為に$1$本引き、
当たりくじかどうかを確認してから元に戻す試行を、
当たりくじが出るまで繰り返す。
当たりくじが出たときのみ得点を得ることができ、
$n$回目にの試行で当たりくじが出た場合、
得られる得点は$50n$点とする。
$n$回目に得られる得点の期待値を$E_n$とする。
ただし、$n$は自然数とする。
(1)$5$回目までに当たりくじが出る確率は$\boxed{ノ}$である。
(2)$\dfrac{E_n}{E_{n+1}}=\dfrac{10}{7}$であるとき、$n=\boxed{ハ}$である。
(3)$\displaystyle \lim_{n\to\infty}\dfrac{E_n}{E_{n+1}}$を求めると$\boxed{ヒ}$である。
(4)$\displaystyle \sum_{k=1}^{n}E_k$を$n$の式で表すと$\boxed{フ}$であり、
$\displaystyle \sum_{k=1}^{\infty}E_k$を求めると$\boxed{ヘ}$である。
ただし、$\vert r \vert \lt 1$を満たす実数$r$に対し、
$\displaystyle \lim_{n\to\infty}n \times r^n=0$が
成り立つこととする。
$2025$年慶應義塾大学薬学部過去問題
福田のおもしろ数学467〜不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a,b,c$を正の数とするとき、
不等式
$\sqrt{a^2-ab+b^2}+\sqrt{b^2-bc+c^2} \geqq \sqrt{a^2+ac+c^2}$
を証明して下さい。
この動画を見る
$a,b,c$を正の数とするとき、
不等式
$\sqrt{a^2-ab+b^2}+\sqrt{b^2-bc+c^2} \geqq \sqrt{a^2+ac+c^2}$
を証明して下さい。
福田の数学〜慶應義塾大学薬学部2025第3問〜逆関数と定積分
単元：
#大学入試過去問(数学)#関数と極限#積分とその応用#関数（分数関数・無理関数・逆関数と合成関数）#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
実数$x$に対して、関数
$f(x)=\dfrac{1}{3}x+\sqrt{\dfrac{1}{9}x^2+8}$
がある。ただし、定義域は$x\geqq 0$である。
$y=f(x)$の逆関数を$y=g(x)$とする。
(1)$g(x)$を求めると、$g(x)=\boxed{ナ}$であり、
$g(x)$定義域は$\boxed{ニ}$である。
(2)$\displaystyle \int_{2\sqrt2}^{4}g(x)dx$を求めると$\boxed{ヌ}$である。
(3)$\displaystyle \int_{0}^{3} f(x) dx$を求めると$\boxed{ネ}$である。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{3}$
実数$x$に対して、関数
$f(x)=\dfrac{1}{3}x+\sqrt{\dfrac{1}{9}x^2+8}$
がある。ただし、定義域は$x\geqq 0$である。
$y=f(x)$の逆関数を$y=g(x)$とする。
(1)$g(x)$を求めると、$g(x)=\boxed{ナ}$であり、
$g(x)$定義域は$\boxed{ニ}$である。
(2)$\displaystyle \int_{2\sqrt2}^{4}g(x)dx$を求めると$\boxed{ヌ}$である。
(3)$\displaystyle \int_{0}^{3} f(x) dx$を求めると$\boxed{ネ}$である。
$2025$年慶應義塾大学薬学部過去問題
福田のおもしろ数学466〜2次方程式の解の条件
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
方程式
$x^2+(a-2)x-2a^2+5a-3=0$
の解の一方の絶対値が、
もう一方の絶対値の$2$倍であるとき、
$a$の全ての値を求めよ。
この動画を見る
方程式
$x^2+(a-2)x-2a^2+5a-3=0$
の解の一方の絶対値が、
もう一方の絶対値の$2$倍であるとき、
$a$の全ての値を求めよ。
福田の数学〜慶應義塾大学薬学部2025第2問〜薬の効果を検定する
単元：
#大学入試過去問(数学)#確率分布と統計的な推測#確率分布#学校別大学入試過去問解説(数学)#標本調査#慶應義塾大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
薬を病気にかかっている患者に投与すると、
投与された患者のうちの$40$% に治療の効果が認められる。
この薬に対し、新しく開発した薬$\beta$の方が
治療の効果が認められる割合が高いかどうか、
有意水準$5$%で検定を行う。
病気$X$にかかっている患者から無作為に抽出した$1000$人に
薬を投与したとき、
$n$人以上に治療の効果が認められると、
薬$\alpha$よりも薬$\beta$の方が効果が認められる割合が高いと判断される。
ただし、薬の治療効果の標本比率を$R$、母比率を$p$とする。
(1) 帰無仮説$H_0$と対立仮説$H_1$に設定する式は
$H_0:\boxed{チ},H_1:\boxed{ツ}$である。
$H_0$が正しいと仮定するとき、
$R$は近似的に正規分布$N(\boxed{テ},\boxed{ト})$に従う。
(2) (1) をふまえ、
$n$のとりうる最小の値を求めなさい。
ただし、解答に
「標準正規分布」と「棄却域」という言葉を含めなさい。
なお、
$\sqrt{2}=1.4,\sqrt3=1.7,\sqrt5 = 2.2$として計算し、
必要に応じて正規分布表を用いなさい。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{2}$
薬を病気にかかっている患者に投与すると、
投与された患者のうちの$40$% に治療の効果が認められる。
この薬に対し、新しく開発した薬$\beta$の方が
治療の効果が認められる割合が高いかどうか、
有意水準$5$%で検定を行う。
病気$X$にかかっている患者から無作為に抽出した$1000$人に
薬を投与したとき、
$n$人以上に治療の効果が認められると、
薬$\alpha$よりも薬$\beta$の方が効果が認められる割合が高いと判断される。
ただし、薬の治療効果の標本比率を$R$、母比率を$p$とする。
(1) 帰無仮説$H_0$と対立仮説$H_1$に設定する式は
$H_0:\boxed{チ},H_1:\boxed{ツ}$である。
$H_0$が正しいと仮定するとき、
$R$は近似的に正規分布$N(\boxed{テ},\boxed{ト})$に従う。
(2) (1) をふまえ、
$n$のとりうる最小の値を求めなさい。
ただし、解答に
「標準正規分布」と「棄却域」という言葉を含めなさい。
なお、
$\sqrt{2}=1.4,\sqrt3=1.7,\sqrt5 = 2.2$として計算し、
必要に応じて正規分布表を用いなさい。
$2025$年慶應義塾大学薬学部過去問題
福田のおもしろ数学465〜最小公倍数を含んだ3項間漸化式
単元：
#数列#漸化式#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$x_1=19,x_2=95$
$x_{n+2}=1cm(x_{n+1},x_n)+x_n$
を満たす数列$\{x_n\}$に対して
$x_{2025}$と$x_{2026}$の最大公約数を求めよ。
＊$1cm(a,b)$は$a$と$b$の最小公倍数を表す。
この動画を見る
$x_1=19,x_2=95$
$x_{n+2}=1cm(x_{n+1},x_n)+x_n$
を満たす数列$\{x_n\}$に対して
$x_{2025}$と$x_{2026}$の最大公約数を求めよ。
＊$1cm(a,b)$は$a$と$b$の最小公倍数を表す。
福田の数学〜慶應義塾大学薬学部2025第1問(5)〜複素数平面上の正n角形の頂点に関する性質
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(5)$n$は$n\geqq 3$を満たす自然数とする。
複素数$z$を$\cos\dfrac{2\pi}{n}+i\sin \dfrac{2\pi}{n}$とおき、
複素数平面において$z^k (0\leqq k \leqq n-1)$が表す点を
$P_k$とする。
ただし、$k$は整数、$i$は虚数単位とする。
(i)$n$個の点$P_0,P_1,P_2,\cdots P_{n-1}$を
頂点とする正$n$角形の面積を$S_n$とする。
$S_n$を$n$の式で表すと$S_n=\boxed{シ}$であり、
$\displaystyle \lim_{n\to\infty}S_n$を求めると$\boxed{ス}$である。
(ii)$\displaystyle \sum_{k=1}^{n-1} z^k$を求めると$\boxed{ス}$である。
(iii)$n=7$とする。
三角形$P_1P_2P_4$の重心を$A(\alpha)$、
三角形$P_3P_5P_6$の重心を$B(\beta)$とおく。
複素数$\alpha,\beta$を求めると、
$\alpha=\boxed{ソ},\beta=\boxed{タ}$である。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{1}$
(5)$n$は$n\geqq 3$を満たす自然数とする。
複素数$z$を$\cos\dfrac{2\pi}{n}+i\sin \dfrac{2\pi}{n}$とおき、
複素数平面において$z^k (0\leqq k \leqq n-1)$が表す点を
$P_k$とする。
ただし、$k$は整数、$i$は虚数単位とする。
(i)$n$個の点$P_0,P_1,P_2,\cdots P_{n-1}$を
頂点とする正$n$角形の面積を$S_n$とする。
$S_n$を$n$の式で表すと$S_n=\boxed{シ}$であり、
$\displaystyle \lim_{n\to\infty}S_n$を求めると$\boxed{ス}$である。
(ii)$\displaystyle \sum_{k=1}^{n-1} z^k$を求めると$\boxed{ス}$である。
(iii)$n=7$とする。
三角形$P_1P_2P_4$の重心を$A(\alpha)$、
三角形$P_3P_5P_6$の重心を$B(\beta)$とおく。
複素数$\alpha,\beta$を求めると、
$\alpha=\boxed{ソ},\beta=\boxed{タ}$である。
$2025$年慶應義塾大学薬学部過去問題
福田のおもしろ数学464〜素数でないことを証明する
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
正の整数$a,b,c,d$が
$ab=cd$を満たすとする。
このとき、
$a+b+c+d$が
素数でないことを証明せよ。
この動画を見る
正の整数$a,b,c,d$が
$ab=cd$を満たすとする。
このとき、
$a+b+c+d$が
素数でないことを証明せよ。
福田の数学〜慶應義塾大学薬学部2025第1問(4)〜円柱を切ってできる立体の体積と側面積
単元：
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#立体図形#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(4)$xyz$空間において、
$xy$平面上に$(0,0,0)$を中心とする半径$2$の円がある。
この円と、$(0,0,2\sqrt3)$を中心とする半径$2$の円を
底面とする円柱を、
原点を通り$xz$平面と$30$度の角をなす平面によって
切断し、$2$つの立体に分ける。
いま$2$つの立体のうち、
体積の小さい方の立体について考える。
その立体の体積を$V$、切り口の面積を$S_1$、
円柱の側面であった部分の面積を$S_2$とする。
(i)$V=\boxed{ケ}$
(ii)$S_1=\boxed{コ},S_2=\boxed{サ}$である。
この動画を見る
$\boxed{1}$
(4)$xyz$空間において、
$xy$平面上に$(0,0,0)$を中心とする半径$2$の円がある。
この円と、$(0,0,2\sqrt3)$を中心とする半径$2$の円を
底面とする円柱を、
原点を通り$xz$平面と$30$度の角をなす平面によって
切断し、$2$つの立体に分ける。
いま$2$つの立体のうち、
体積の小さい方の立体について考える。
その立体の体積を$V$、切り口の面積を$S_1$、
円柱の側面であった部分の面積を$S_2$とする。
(i)$V=\boxed{ケ}$
(ii)$S_1=\boxed{コ},S_2=\boxed{サ}$である。
福田のおもしろ数学463〜2定点を見込む角を最大にする方法
単元：
#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学(高校生)#数Ⅲ
指導講師：
福田次郎
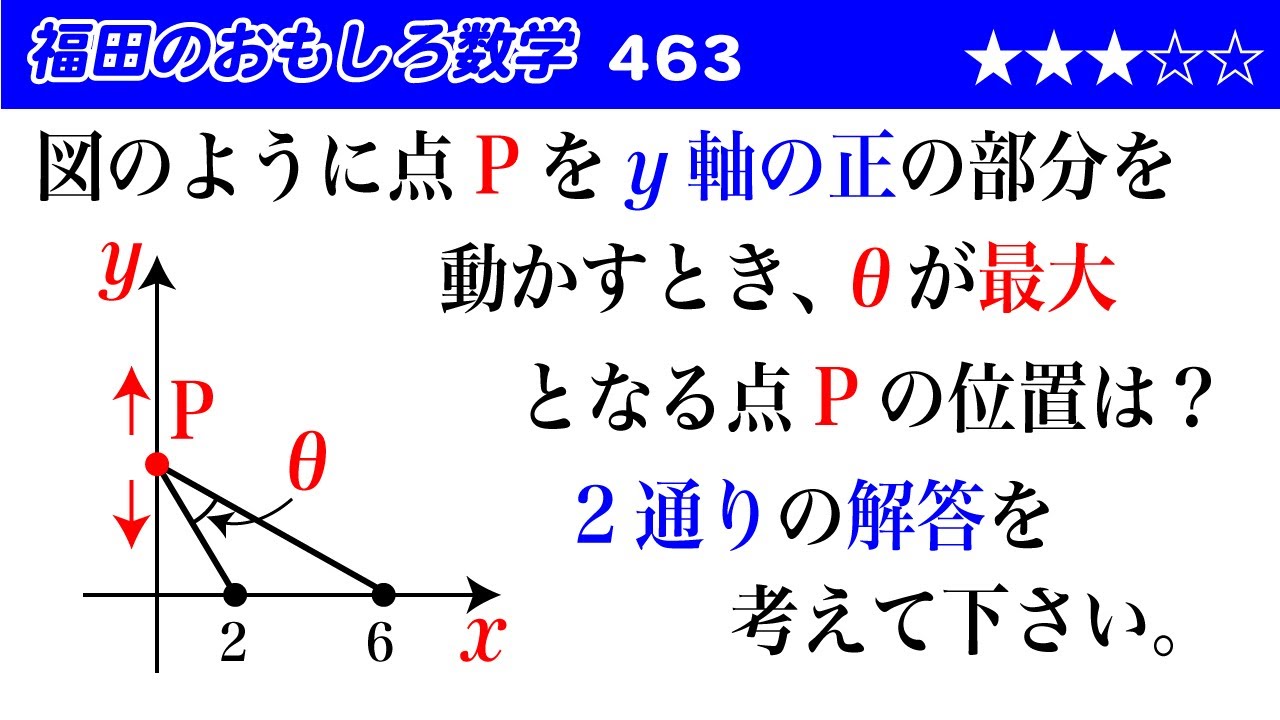
問題文全文(内容文)：
図のように点$P$を$y$軸の正の部分を
動かすとき、
$\theta$が最大となる点$P$の位置は？
$2$通りの解答を考えて下さい。
図は動画内参照
この動画を見る
図のように点$P$を$y$軸の正の部分を
動かすとき、
$\theta$が最大となる点$P$の位置は？
$2$通りの解答を考えて下さい。
図は動画内参照
福田の数学〜慶應義塾大学薬学部2025第1問(3)〜絶対値の付いた対数関数の最小
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(3)実数$x$に対して、関数
$f(x)=\left \vert \dfrac{1}{10^{-x}\log 10^{-x}}\right \vert$
は、$x=\boxed{キ}$のとき最小値$\boxed{ク}$をとる。
ただし、$x$は$x\gt 0$を満たし、対数は自然対数とする。
なお、$\log 2=0.69,\log 3=1.10,\log 5=1.61,$
自然対数の底$e$は$2.72$として計算し、
$\boxed{キ}$と$\boxed{ク}$は小数で答えなさい。
値が小数第$2$位までで割り切れない場合は、
小数第$3$位を四捨五入して小数第$2$位まで求めなさい。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{1}$
(3)実数$x$に対して、関数
$f(x)=\left \vert \dfrac{1}{10^{-x}\log 10^{-x}}\right \vert$
は、$x=\boxed{キ}$のとき最小値$\boxed{ク}$をとる。
ただし、$x$は$x\gt 0$を満たし、対数は自然対数とする。
なお、$\log 2=0.69,\log 3=1.10,\log 5=1.61,$
自然対数の底$e$は$2.72$として計算し、
$\boxed{キ}$と$\boxed{ク}$は小数で答えなさい。
値が小数第$2$位までで割り切れない場合は、
小数第$3$位を四捨五入して小数第$2$位まで求めなさい。
$2025$年慶應義塾大学薬学部過去問題
福田のおもしろ数学462〜2n+1角形の頂点と辺に異なる整数を割り当てて辺上の合計を等しくする方法
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$2n+1$個の頂点をもつ多角形がある。
この多角形の頂点と辺の中点に数
$1,2,3,\cdots,4n+2$をすべて使用してラベルをつけ、
各辺に割り当てられた
$3$つの数の和が等しくなるようにせよ。
この動画を見る
$2n+1$個の頂点をもつ多角形がある。
この多角形の頂点と辺の中点に数
$1,2,3,\cdots,4n+2$をすべて使用してラベルをつけ、
各辺に割り当てられた
$3$つの数の和が等しくなるようにせよ。
福田の数学〜慶應義塾大学薬学部2025第1問(2)〜正八面体に内接する立方体の体積
単元：
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#立体図形#立体切断#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(2)$a$は$a\gt 0$を満たす実数とする。
$xyz$空間に$6$点$(a,0,0),(0,a,0),(0,0,a),$
$(-a,0,0)(0,-a,0)(0,0,-a)$を頂点とする多面体
$S$がある。
(i)$S$の体積は$\boxed{オ}$である。
(ii)立方体$U$のすべての頂点が$S$の辺上にあるとき、
$U$の体積は$\boxed{カ}$である。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{1}$
(2)$a$は$a\gt 0$を満たす実数とする。
$xyz$空間に$6$点$(a,0,0),(0,a,0),(0,0,a),$
$(-a,0,0)(0,-a,0)(0,0,-a)$を頂点とする多面体
$S$がある。
(i)$S$の体積は$\boxed{オ}$である。
(ii)立方体$U$のすべての頂点が$S$の辺上にあるとき、
$U$の体積は$\boxed{カ}$である。
$2025$年慶應義塾大学薬学部過去問題
福田のおもしろ数学461〜関数方程式
単元：
#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$0$以上の実数で定義された実数値関数$f(x)$は
(i)$f(1)=1$
(ii)$f\left(\dfrac{1}{x+y}\right)=f\left(\dfrac{1}{x}\right)+f\left(\dfrac{1}{y}\right)$
$ \hspace{ 100pt } (x+y,x,y\neq 0)$
(iii)$(x+y)f(x+y)=xyf(x)f(y)$
$\hspace{ 100pt }(x+y,x,y\neq 0)$
を満たしている。$f(x)$を求めよ。
この動画を見る
$0$以上の実数で定義された実数値関数$f(x)$は
(i)$f(1)=1$
(ii)$f\left(\dfrac{1}{x+y}\right)=f\left(\dfrac{1}{x}\right)+f\left(\dfrac{1}{y}\right)$
$ \hspace{ 100pt } (x+y,x,y\neq 0)$
(iii)$(x+y)f(x+y)=xyf(x)f(y)$
$\hspace{ 100pt }(x+y,x,y\neq 0)$
を満たしている。$f(x)$を求めよ。