ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題をベースに数学の動画を作成しています。大学過去問を多数解説しています。
頻繁に更新していますので是非ご視聴ください！
職業：数学者
職歴：高校非常勤（院生時代）、高専、大学 准教授
趣味：
①将棋 棋力は将棋ウォーズ４段、将棋倶楽部２４はR２０００前後（小学校５，６年のころに頑張ってました）
②麻雀 アカウントは消えましたが、無課金で天鵬で７段まで上がりました。
③ソフトテニス 中学から大学まで、１０年間部活でやっていました。大学時代は４年になってもリーグにでていました。
大学入試問題#92 東京医科大学(2015) 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}(x\sqrt{ 1-x^2 })^3 dx$を計算せよ。
出典：2015年東京医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}(x\sqrt{ 1-x^2 })^3 dx$を計算せよ。
出典：2015年東京医科大学 入試問題
大学入試問題#91 関西学院大学(2006) 不定積分
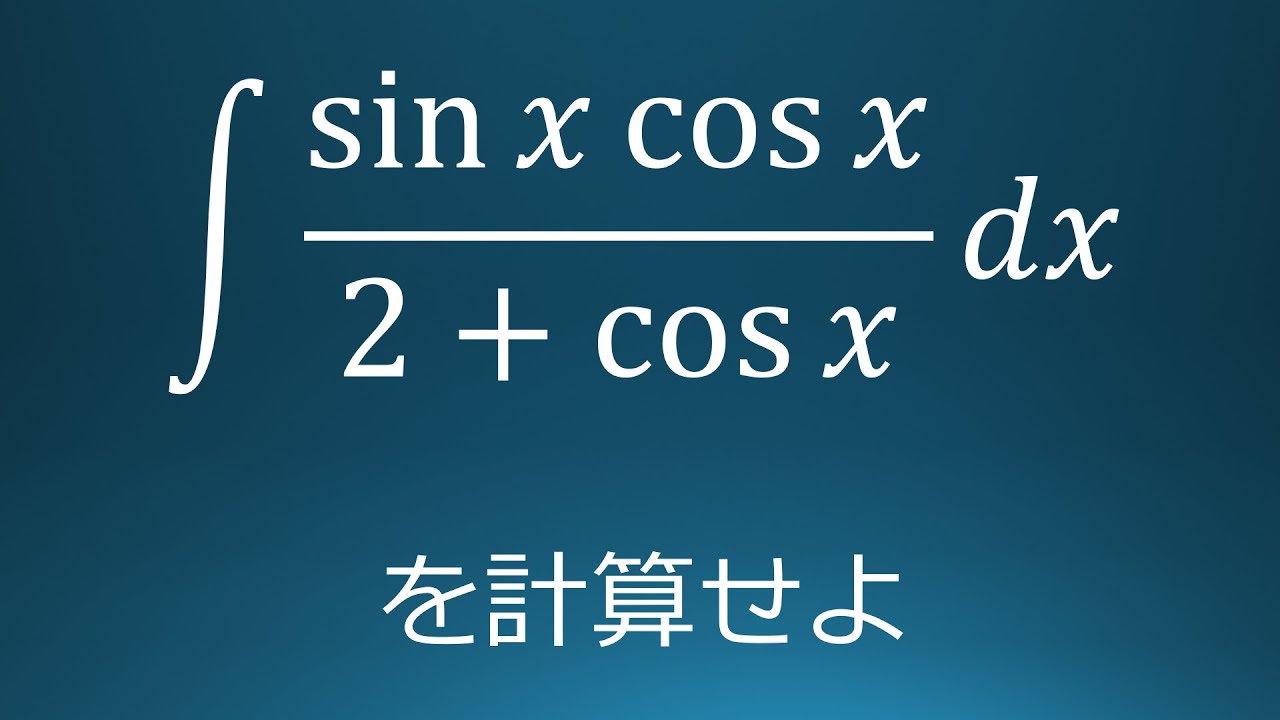
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{\sin\ x\ \cos\ x}{2+\cos\ x}\ dx$を計算せよ。
出典：2006年関西学院大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{\sin\ x\ \cos\ x}{2+\cos\ x}\ dx$を計算せよ。
出典：2006年関西学院大学 入試問題
大学入試問題#90 京都大学(2001) 整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x,y,z$：正の整数
$x^2+2y^2+2z^2-2xy-2xz+2yz-5=0$をみたす組（$x,y,z$）をすべて求めよ。
出典：2001年京都大学 入試問題
この動画を見る
$x,y,z$：正の整数
$x^2+2y^2+2z^2-2xy-2xz+2yz-5=0$をみたす組（$x,y,z$）をすべて求めよ。
出典：2001年京都大学 入試問題
大学入試問題#89 信州大学(1988) 不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int (x^2+a^2)^{-\frac{3}{2}}dx$
$a \neq 0$を計算せよ。
出典：1988年信州大学 入試問題
この動画を見る
$\displaystyle \int (x^2+a^2)^{-\frac{3}{2}}dx$
$a \neq 0$を計算せよ。
出典：1988年信州大学 入試問題
数学ゴールデン【漫画】で紹介された数オリの問題の解答がなかったから作成してみた。
単元：
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#式の計算（整式・展開・因数分解）#数学オリンピック#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$0 \lt x$：実数
$x+\sqrt{ x(x+1) }+\sqrt{ x(x+2) }+\sqrt{ (x+1)(x+2) }=2$を解け。
出典：数学ゴールデン 数学オリンピック
この動画を見る
$0 \lt x$：実数
$x+\sqrt{ x(x+1) }+\sqrt{ x(x+2) }+\sqrt{ (x+1)(x+2) }=2$を解け。
出典：数学ゴールデン 数学オリンピック
大学入試問題#88 関西大学(2006) 整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師：
ますただ
問題文全文(内容文)：
$x^3+x^2-1=y(x-1)$をみたす整数の組$(x,y)$をすべて求めよ。
出典：2006年関西大学 入試問題
この動画を見る
$x^3+x^2-1=y(x-1)$をみたす整数の組$(x,y)$をすべて求めよ。
出典：2006年関西大学 入試問題
大学入試問題#87 立命館大学(2018) 整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#立命館大学
指導講師：
ますただ
問題文全文(内容文)：
$n$：整数
$\sqrt{ n^2-8n+1 }$が整数となる$n$をすべて求めよ。
出典：2018年立命館大学 入試問題
この動画を見る
$n$：整数
$\sqrt{ n^2-8n+1 }$が整数となる$n$をすべて求めよ。
出典：2018年立命館大学 入試問題
大学入試問題#86 防衛医科大学(1988) 極限
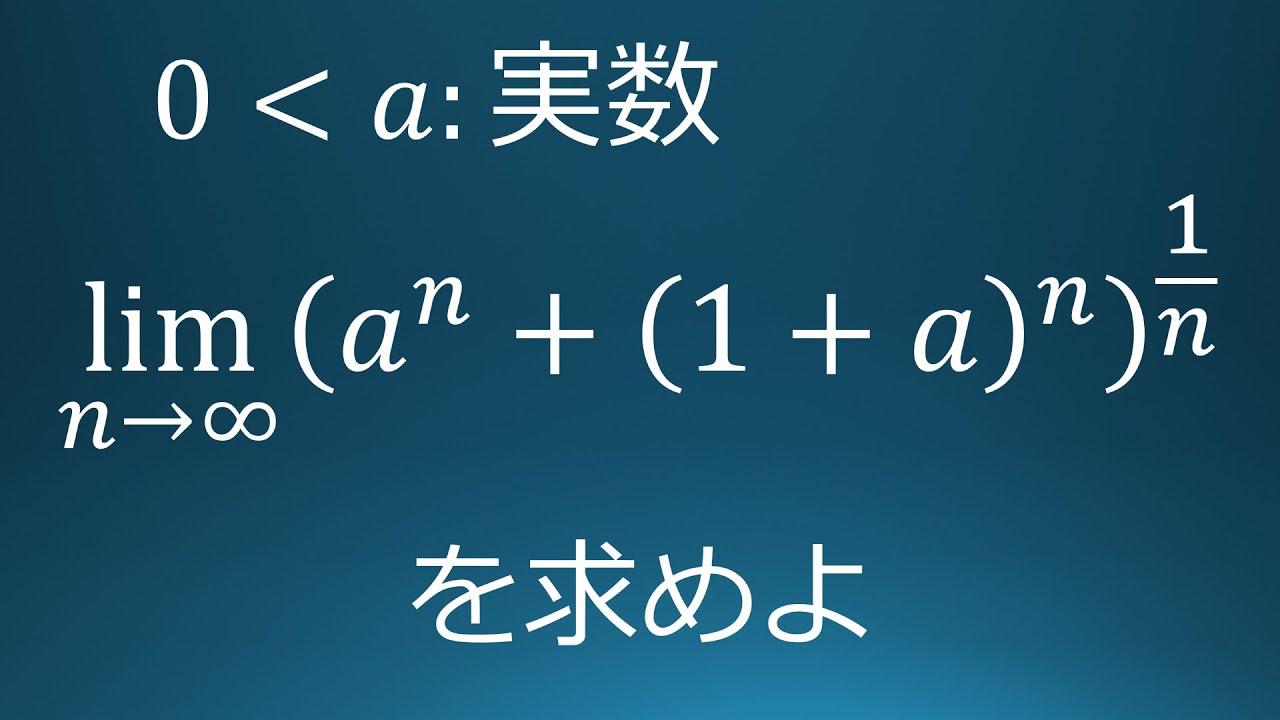
単元：
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師：
ますただ
問題文全文(内容文)：
$0 \lt a$：実数
$\displaystyle \lim_{ n \to \infty }(a^n+(1+a)^n)^{\frac{1}{n}}$を求めよ。
出典：1988年防衛医科大学 入試問題
この動画を見る
$0 \lt a$：実数
$\displaystyle \lim_{ n \to \infty }(a^n+(1+a)^n)^{\frac{1}{n}}$を求めよ。
出典：1988年防衛医科大学 入試問題
大学入試問題#85 小樽商科大学(1988) 不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#小樽商科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \sin(log\ x)dx$を計算せよ。
出典：1988年小樽商科大学 入試問題
この動画を見る
$\displaystyle \int \sin(log\ x)dx$を計算せよ。
出典：1988年小樽商科大学 入試問題
大学入試問題#84 弘前大学(1986) 不定積分
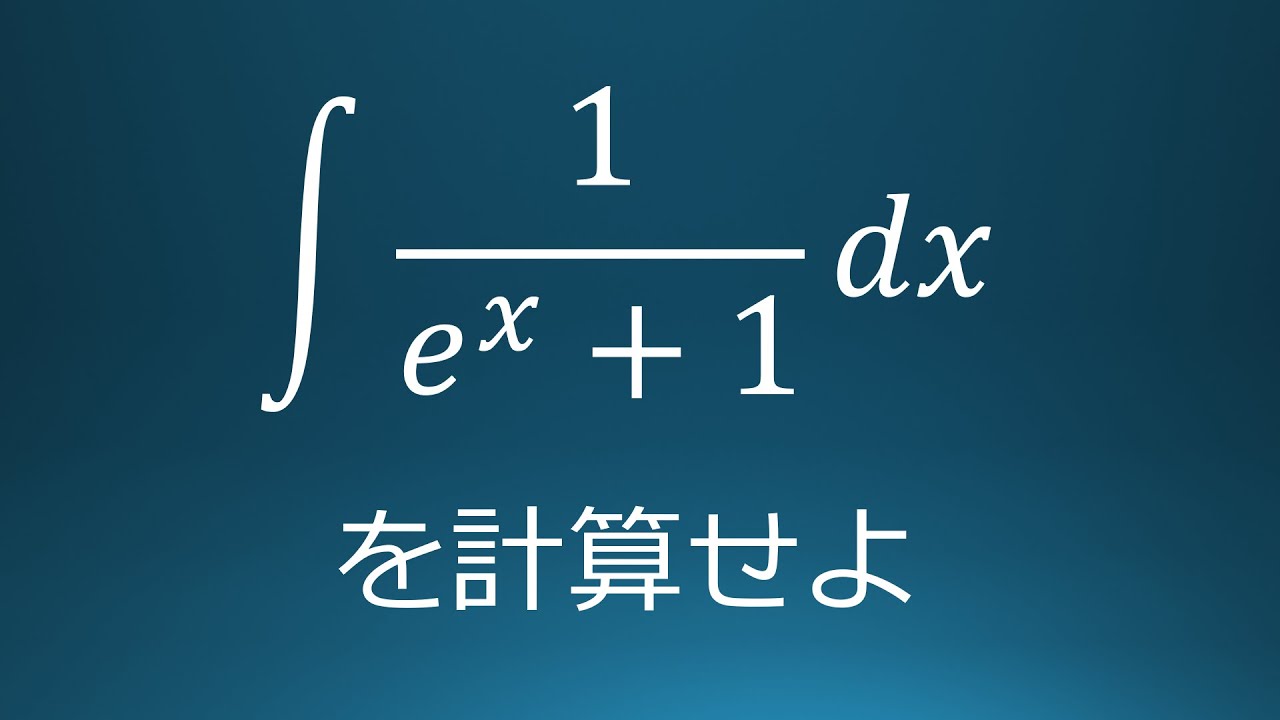
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{1}{e^x+1}\ dx$を計算せよ。
出典：1986年弘前大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{1}{e^x+1}\ dx$を計算せよ。
出典：1986年弘前大学 入試問題
大学入試問題#83 京都大学(2012) 平面ベクトル
単元：
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$\triangle OAB$において
$OA=3,\ OB=2$
$\angle AOB=60^{ \circ }$
$\triangle OAB$の垂心を$H$とする。
$\overrightarrow{ OH }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$で表せ。
出典：2021年京都大学 入試問題
この動画を見る
$\triangle OAB$において
$OA=3,\ OB=2$
$\angle AOB=60^{ \circ }$
$\triangle OAB$の垂心を$H$とする。
$\overrightarrow{ OH }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$で表せ。
出典：2021年京都大学 入試問題
大学入試問題#82 神戸大学(2012) 複雑な置換積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\sin\ x-\cos\ x}{1+\cos\ x}\ dx$
出典：2012年神戸大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\sin\ x-\cos\ x}{1+\cos\ x}\ dx$
出典：2012年神戸大学 入試問題
大学入試問題#81 東京大学(2012) ２次方程式【正確な問題文は概要欄】
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x,y$：実数
$2x^2+4xy+3y^2+4x+5y-4=0$を満たすとき、$x$のとりうる最大の値を求めよ。
出典：2012年東京大学 入試問題
この動画を見る
$x,y$：実数
$2x^2+4xy+3y^2+4x+5y-4=0$を満たすとき、$x$のとりうる最大の値を求めよ。
出典：2012年東京大学 入試問題
大学入試問題#80 信州大学(2001) 不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ x+1 }+1}\ dx$を計算せよ。
出典：2001年信州大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ x+1 }+1}\ dx$を計算せよ。
出典：2001年信州大学 入試問題
【全ての問題は概要欄】大学入試問題#79 大阪大学(2020 改) 微分
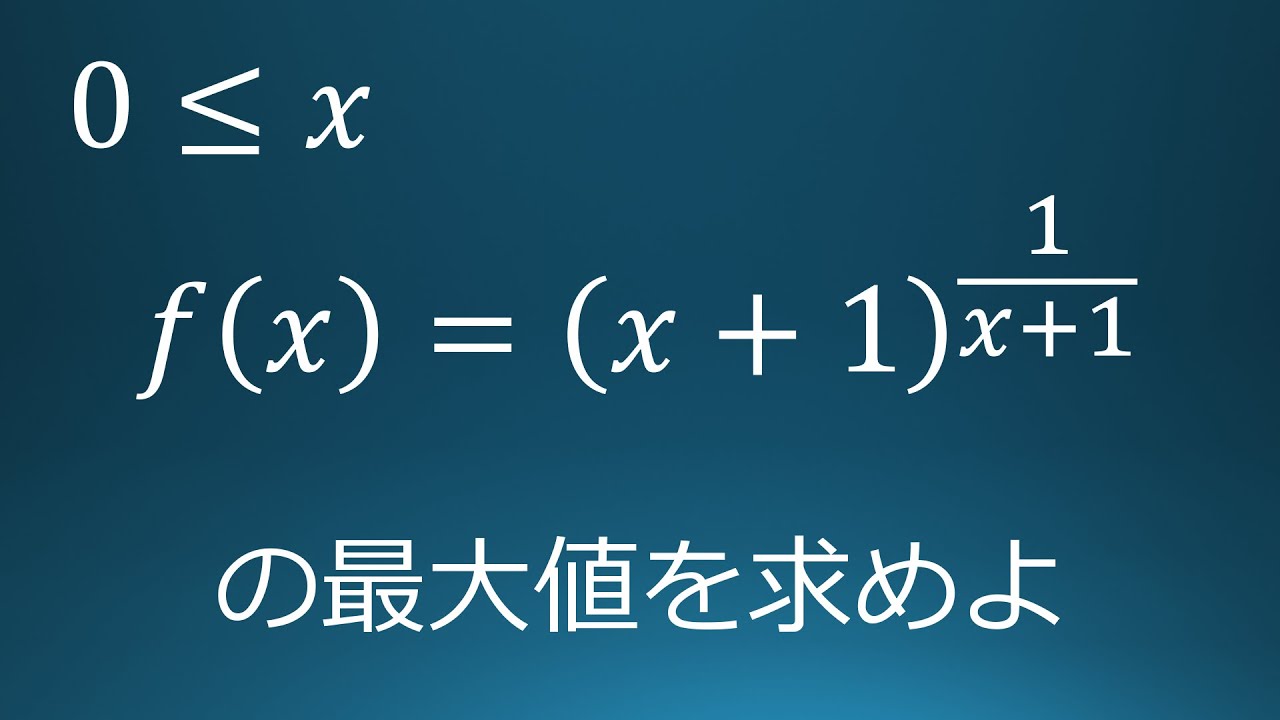
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$0 \leqq x$
関数$f(x)=(x+1)^{\frac{1}{x+1}}$の最大値を求めよ。
出典：2020年大阪大学 入試問題
この動画を見る
$0 \leqq x$
関数$f(x)=(x+1)^{\frac{1}{x+1}}$の最大値を求めよ。
出典：2020年大阪大学 入試問題
大学入試問題#78 横浜国立大学(2006) 置換積分
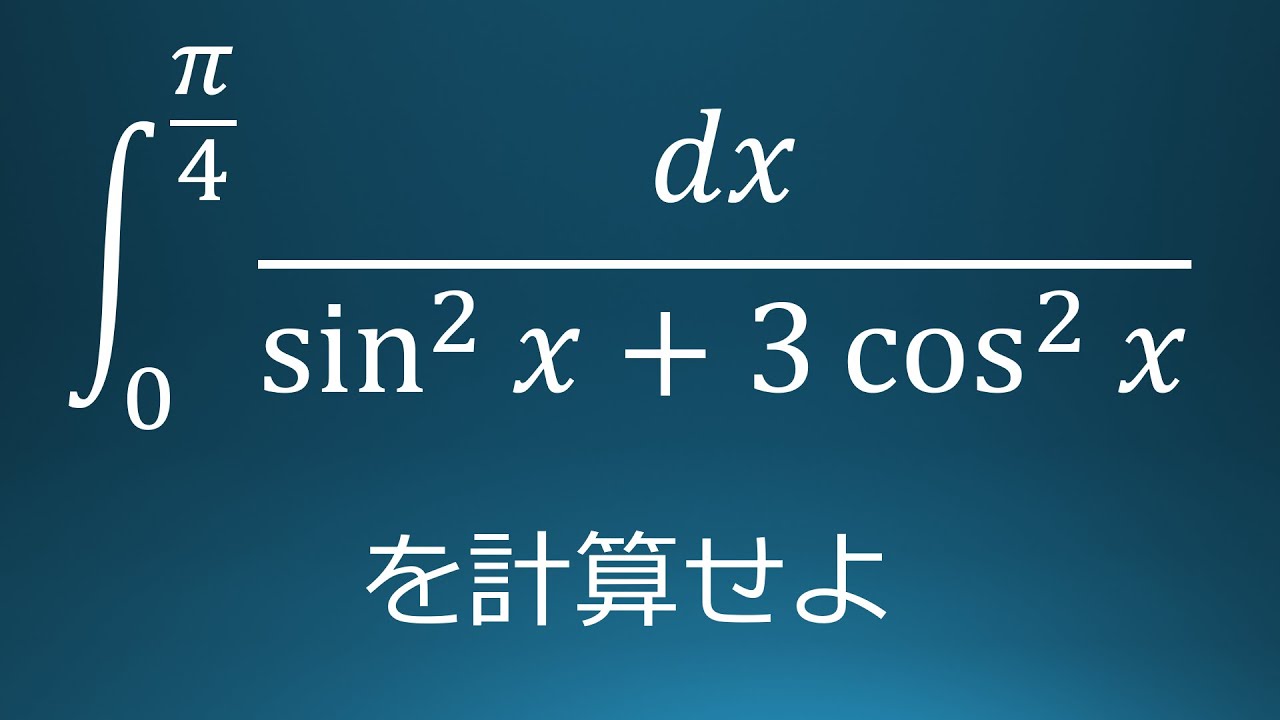
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{dx}{\sin^2x+3\cos^2x}$を計算せよ。
出典：2006年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{dx}{\sin^2x+3\cos^2x}$を計算せよ。
出典：2006年横浜国立大学 入試問題
大学入試問題#77 京都大学(2002) 数列と極限
単元：
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$a_1=1,\displaystyle \lim_{ n \to \infty }S_n=1$
$n(n-2)a_{n+1}=s_n$のとき
一般項$a_n$を求めよ。
出典：2002年京都大学 入試問題
この動画を見る
$a_1=1,\displaystyle \lim_{ n \to \infty }S_n=1$
$n(n-2)a_{n+1}=s_n$のとき
一般項$a_n$を求めよ。
出典：2002年京都大学 入試問題
【概要欄に正確な文章と説明の補足】大学入試問題#76 京都大学(2007) 数列と極限
単元：
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$x,y$：異なる正の実数
$a_1=0$
$a_{n+1}=x a_n=s\ a_n+y^{n+1}$のとき
$\displaystyle \lim_{ n \to \infty }a_n \lt \infty$となるような$(x,y)$の範囲を図示せよ。
出典：2007年京都大学 入試問題
この動画を見る
$x,y$：異なる正の実数
$a_1=0$
$a_{n+1}=x a_n=s\ a_n+y^{n+1}$のとき
$\displaystyle \lim_{ n \to \infty }a_n \lt \infty$となるような$(x,y)$の範囲を図示せよ。
出典：2007年京都大学 入試問題
大学入試問題#75 横浜国立大学(2006) 部分積分
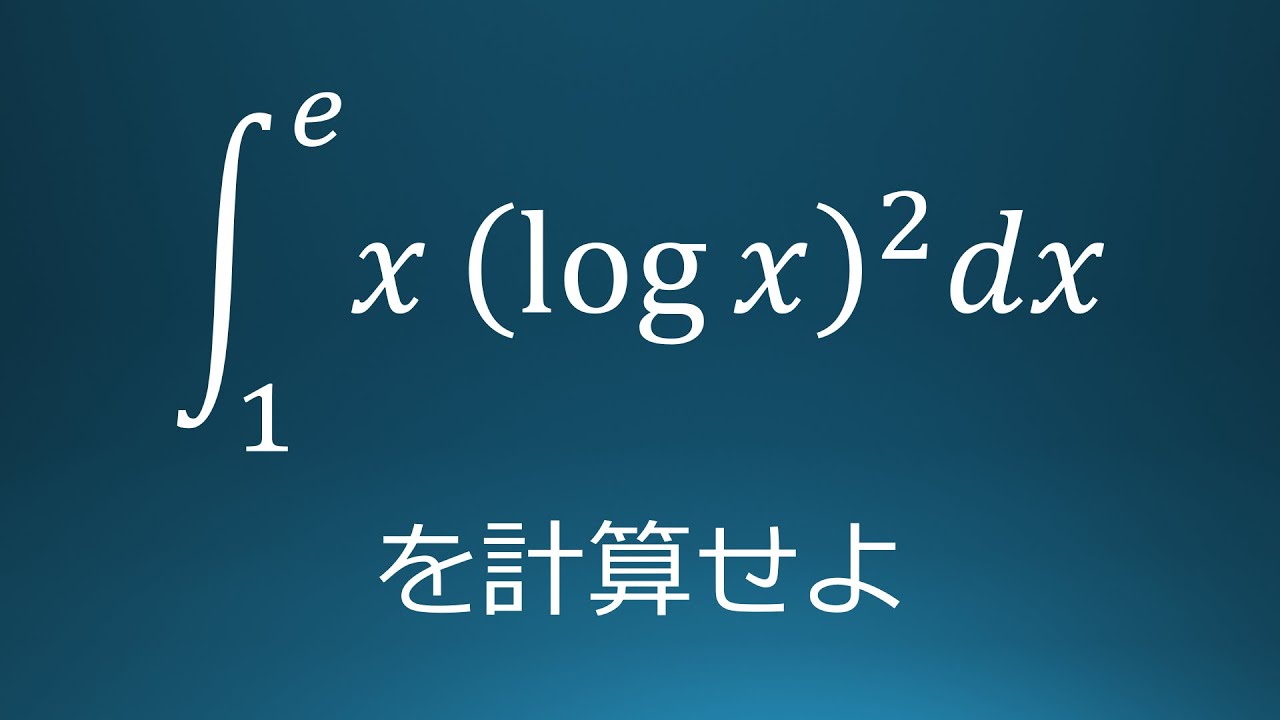
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{e}x(log\ x)^2dx$を計算せよ。
出典：2006年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e}x(log\ x)^2dx$を計算せよ。
出典：2006年横浜国立大学 入試問題
大学入試問題#74 神戸大学(1991) 数列と極限
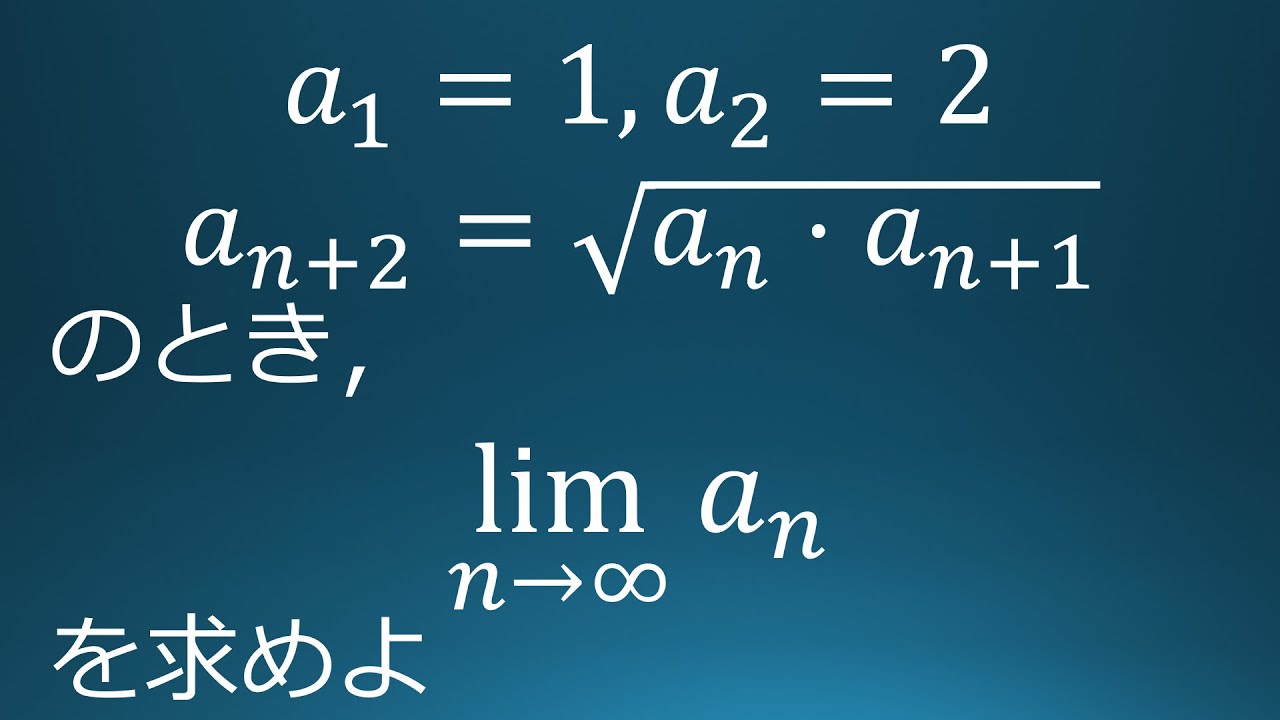
単元：
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数B#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$a_1=1,\ a_2=2$
$a_{n+2}=\sqrt{ a_n\ a_{n+1} }$のとき
$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
出典：1991年神戸大学 入試問題
この動画を見る
$a_1=1,\ a_2=2$
$a_{n+2}=\sqrt{ a_n\ a_{n+1} }$のとき
$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
出典：1991年神戸大学 入試問題
大学入試問題#73 京都大学(2012) 極限
単元：
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$0 \lt a$：実数
$\displaystyle \lim_{ n \to \infty }(1+a^n)^{\frac{1}{n}}$の極限を求めよ。
出典：2012年京都大学 入試問題
この動画を見る
$0 \lt a$：実数
$\displaystyle \lim_{ n \to \infty }(1+a^n)^{\frac{1}{n}}$の極限を求めよ。
出典：2012年京都大学 入試問題
11三重県教員採用試験（数学：1番 整数問題）
単元：
#数A#数Ⅱ#複素数と方程式#整数の性質#約数・倍数・整数の割り算と余り・合同式#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$p$整数
$x^2-3|x+7p=0$の2つの解$\alpha,\beta$自然数とする。
$\alpha,\beta$が最大となる$p$を求めよ。
この動画を見る
$p$整数
$x^2-3|x+7p=0$の2つの解$\alpha,\beta$自然数とする。
$\alpha,\beta$が最大となる$p$を求めよ。
大学入試問題#72 福岡教育大学(2009) 置換積分②
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{log\ 7}(\displaystyle \frac{e^x}{1+e^x})^3dx$を計算せよ。
出典：2009年福岡教育大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{log\ 7}(\displaystyle \frac{e^x}{1+e^x})^3dx$を計算せよ。
出典：2009年福岡教育大学 入試問題
#49 数検1級1次 過去問 根号を外す
単元：
#数Ⅰ#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#数と式#２次関数#複素数と方程式#式の計算（整式・展開・因数分解）#2次方程式と2次不等式#2次関数とグラフ#解と判別式・解と係数の関係#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt[ 3 ]{ -5+2\sqrt{ 13 } }\ $の二重根号をはずせ
この動画を見る
$\sqrt[ 3 ]{ -5+2\sqrt{ 13 } }\ $の二重根号をはずせ
大学入試問題#71 横浜国立大学(2005) 置換積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{log\ 3}{2}}\ \displaystyle \frac{e^x+1}{e^{2x}+1}\ dx$
出典：2005年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{log\ 3}{2}}\ \displaystyle \frac{e^x+1}{e^{2x}+1}\ dx$
出典：2005年横浜国立大学 入試問題
大学入試問題#70 鳥取大学医学部(2012) 微積の応用
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#鳥取大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$a,b$：実数
$0 \lt a \lt 2$
$\displaystyle \int_{a}^{x}f(x-t)f(t)dt=\cos(ax)-b$
（1）$a,b$の値を求めよ。
（2）$f(x)$を求めよ
（3）$f(x)$が最大値をとるときの$x$の値を求めよ。
出典：2012年鳥取大学医学部 入試問題
この動画を見る
$a,b$：実数
$0 \lt a \lt 2$
$\displaystyle \int_{a}^{x}f(x-t)f(t)dt=\cos(ax)-b$
（1）$a,b$の値を求めよ。
（2）$f(x)$を求めよ
（3）$f(x)$が最大値をとるときの$x$の値を求めよ。
出典：2012年鳥取大学医学部 入試問題
大学入試問題#69 高知大学(2012) 数列
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#高知大学#数B
指導講師：
ますただ
問題文全文(内容文)：
各自然数$n$に対して
$a_n \gt 0$
$S_n=\displaystyle \frac{1}{2}a_n^2+\displaystyle \frac{1}{2}a_n-1$をみたす一般項$a_n$を求めよ。
出典：2012年高知大学 入試問題
この動画を見る
各自然数$n$に対して
$a_n \gt 0$
$S_n=\displaystyle \frac{1}{2}a_n^2+\displaystyle \frac{1}{2}a_n-1$をみたす一般項$a_n$を求めよ。
出典：2012年高知大学 入試問題
大学入試問題#68 京都大学(2012) 部分積分
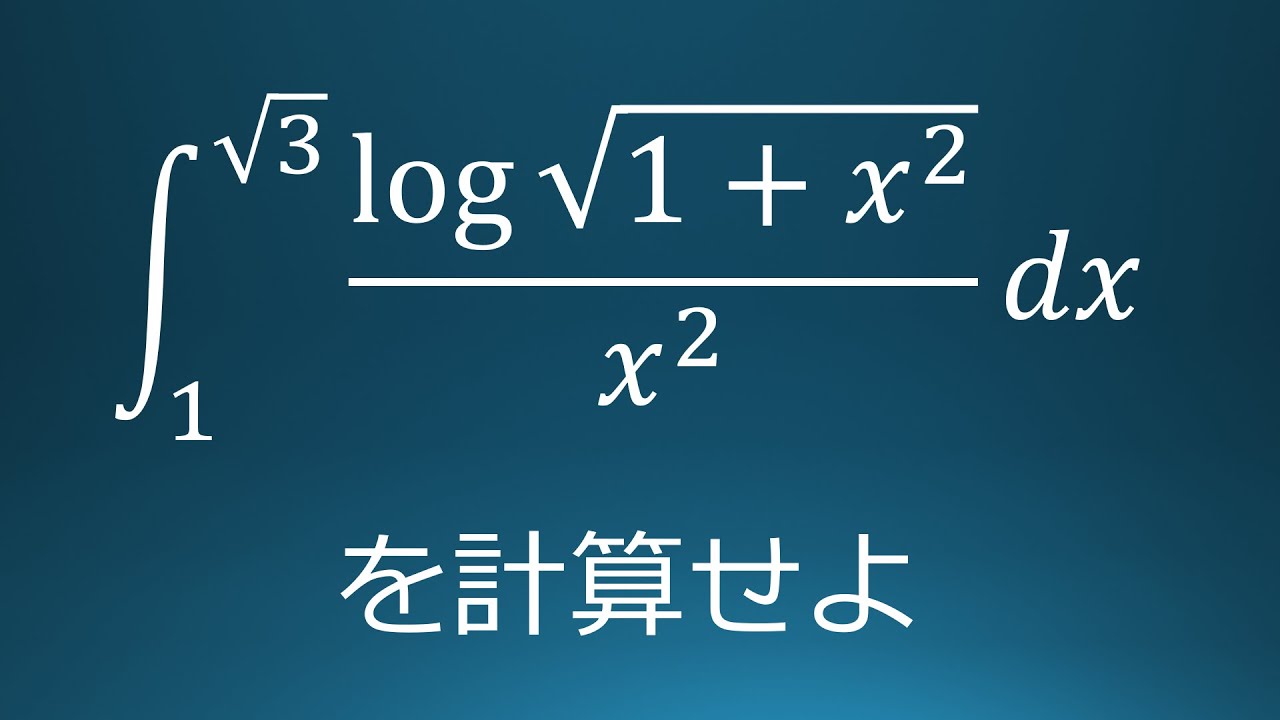
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{\sqrt{ 3 }}\displaystyle \frac{log\sqrt{ 1+x^2 }}{x^2}\ dx$
出典：2012年京都大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{\sqrt{ 3 }}\displaystyle \frac{log\sqrt{ 1+x^2 }}{x^2}\ dx$
出典：2012年京都大学 入試問題
大学入試問題#67 福岡教育大学(2009) 置換積分①
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{log7}(\displaystyle \frac{e^x}{1+e^x})^2dx$を計算せよ。
出典：2009年福岡教育大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{log7}(\displaystyle \frac{e^x}{1+e^x})^2dx$を計算せよ。
出典：2009年福岡教育大学 入試問題
大学入試問題#66 横浜国立大学(2003) 置換積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}\displaystyle \frac{x+1}{(x^2+x^1)^2}\ dx$を計算せよ。
出典：2003年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{x+1}{(x^2+x^1)^2}\ dx$を計算せよ。
出典：2003年横浜国立大学 入試問題