 ますただ
ますただ
 ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
15奈良県教員採用試験(数学:高校3番 軌跡)

単元:
#数Ⅱ#図形と方程式#軌跡と領域#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
3⃣ P(0,a),$y=\frac{x^2}{a}$上の点をQ,
PQは最小値をとる(a≠0)
(1)Qの座標を求めよ。
(2)Qの軌跡を求めよ。
この動画を見る
3⃣ P(0,a),$y=\frac{x^2}{a}$上の点をQ,
PQは最小値をとる(a≠0)
(1)Qの座標を求めよ。
(2)Qの軌跡を求めよ。
15奈良県教員採用試験(数学:3番 式変形)
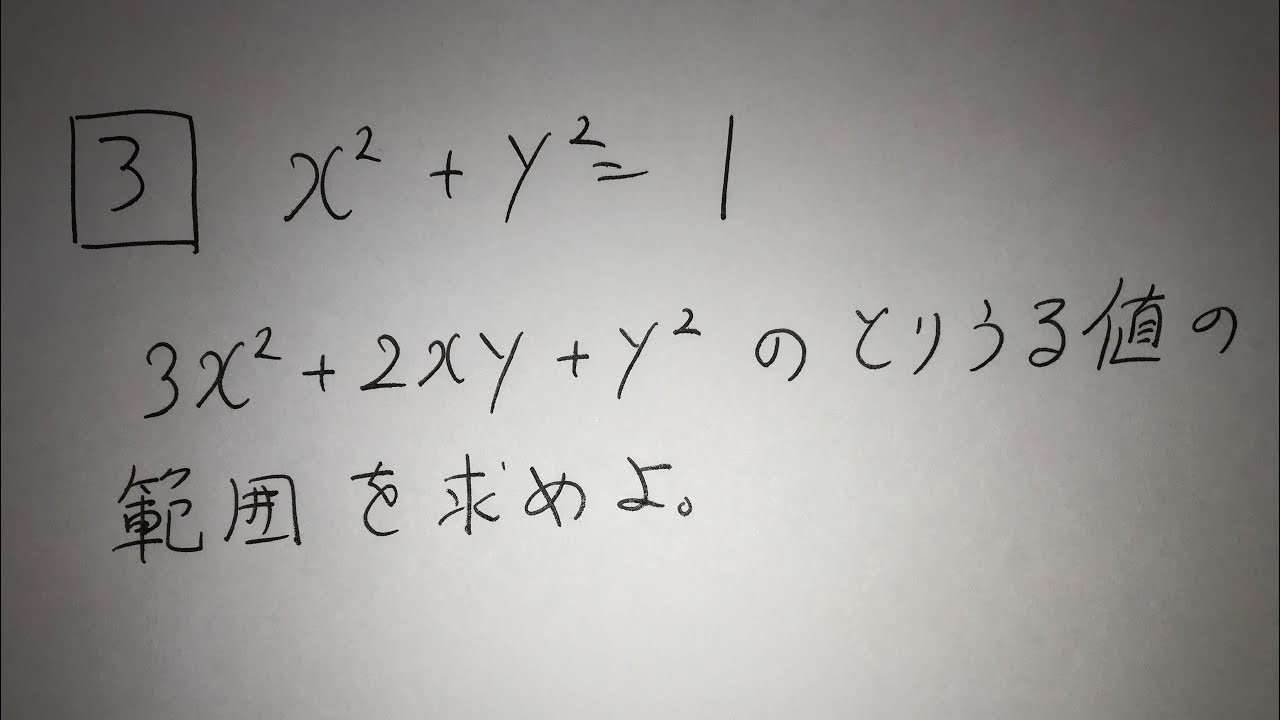
14奈良県教員採用試験(数学:2番 式変形)

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣x=1-y-z
$x^2=1+yz$
(1)$x^3+y^3+z^3$をxで表せ
(2)xの範囲を求めよ。
(3)$x^3+y^3+z^3$の最大値を求めよ。
この動画を見る
2⃣x=1-y-z
$x^2=1+yz$
(1)$x^3+y^3+z^3$をxで表せ
(2)xの範囲を求めよ。
(3)$x^3+y^3+z^3$の最大値を求めよ。
17神奈川県教員採用試験(数学:13番 y軸回転体)

単元:
#積分とその応用#面積・体積・長さ・速度#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{13}$
$y=\frac{1}{2}x^2-x$とx軸で囲まれた領域をy軸を中心としてできる回転体の体積を求めよ。
この動画を見る
$\boxed{13}$
$y=\frac{1}{2}x^2-x$とx軸で囲まれた領域をy軸を中心としてできる回転体の体積を求めよ。
16神奈川県教員採用試験(数学:整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣$n \leqq 300$,nの約数の個数が9個となる$n \in \mathbb{ N }$を求めよ。
この動画を見る
2⃣$n \leqq 300$,nの約数の個数が9個となる$n \in \mathbb{ N }$を求めよ。
19奈良県教員採用試験(数学:高校1番 微分)

単元:
#微分とその応用#微分法#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
高1⃣類題
$f(x)=x \quad sinx がx=aで微分可能を示せ$
この動画を見る
高1⃣類題
$f(x)=x \quad sinx がx=aで微分可能を示せ$
17神奈川県教員採用試験(数学:1番 式変形)
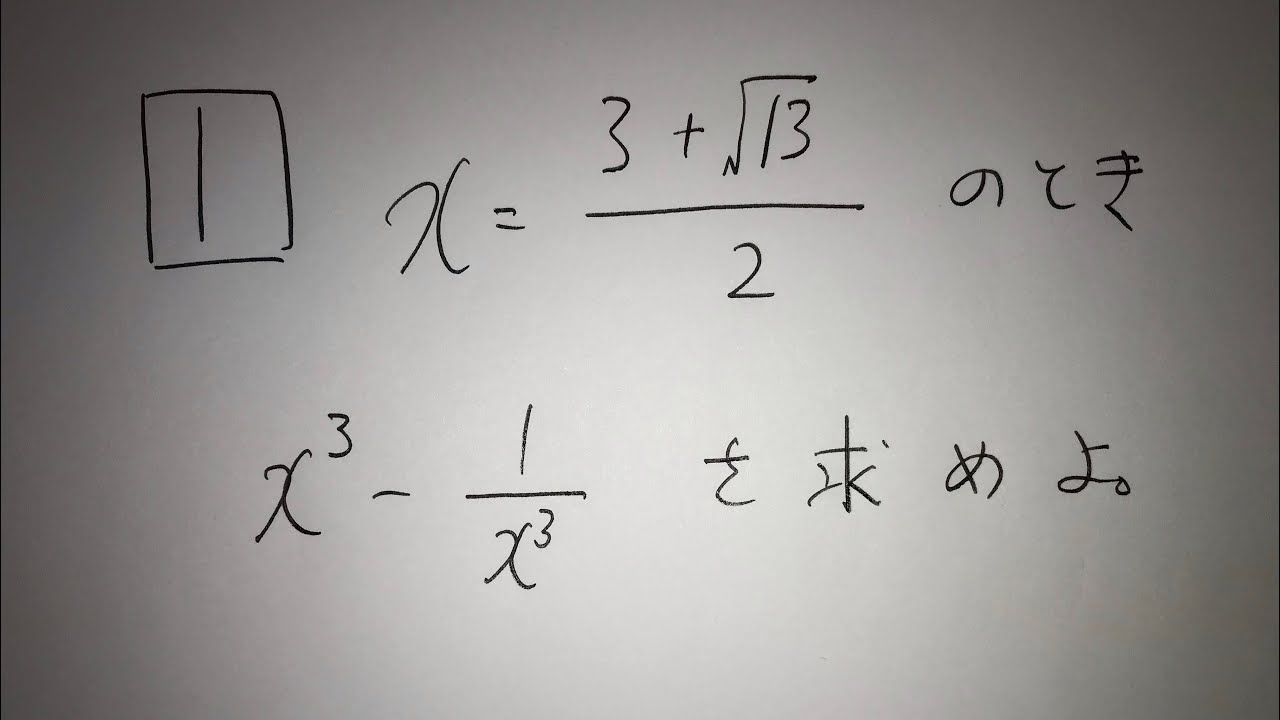
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣$x=\frac{3+\sqrt{13}}{2}$のとき
$x^3-\frac{1}{x^3}$を求めよ。
この動画を見る
1⃣$x=\frac{3+\sqrt{13}}{2}$のとき
$x^3-\frac{1}{x^3}$を求めよ。
19奈良県教員採用試験(数学:3番 数列)
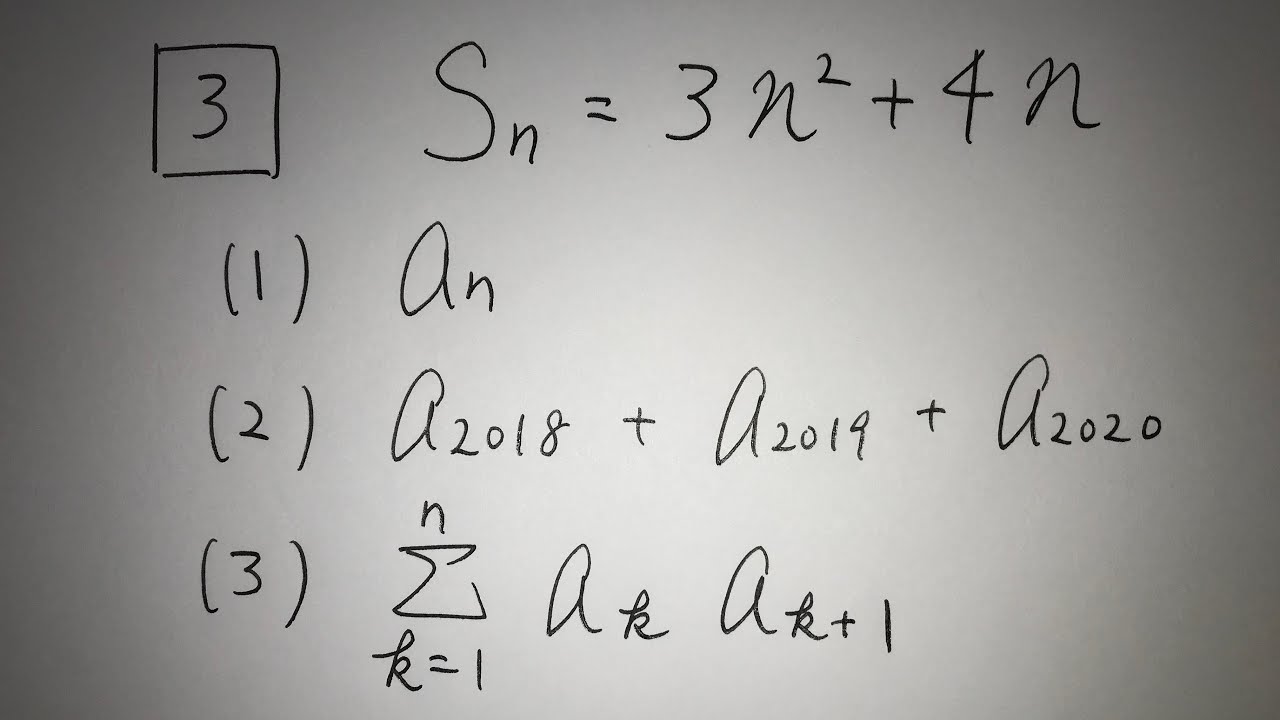
単元:
#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
3⃣$S_n=3n^2+4n$
(1)$a_n$
(2)$a_{2018}+a_{2019}+a_{2020}$
(3)$\displaystyle \sum_{k=1}^n a_k a_{k+1}$
この動画を見る
3⃣$S_n=3n^2+4n$
(1)$a_n$
(2)$a_{2018}+a_{2019}+a_{2020}$
(3)$\displaystyle \sum_{k=1}^n a_k a_{k+1}$
18神奈川県教員採用試験(数学:11番 区分求積法)
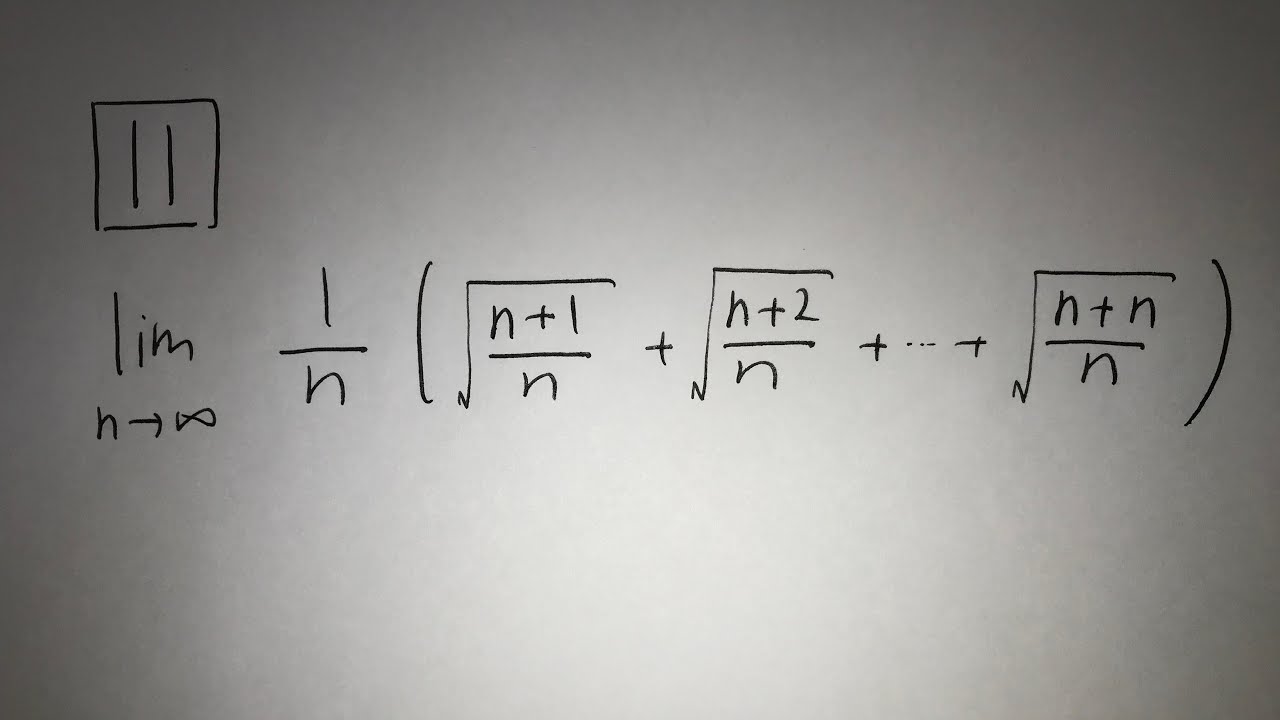
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\fbox{ 11 }$
$\displaystyle \lim_{ n \to \infty } \frac{1}{n}(\sqrt{\frac{n+1}{n}} +\sqrt{\frac{n+2}{n}} + \cdots +\sqrt{\frac{n+n}{n}})$
この動画を見る
$\fbox{ 11 }$
$\displaystyle \lim_{ n \to \infty } \frac{1}{n}(\sqrt{\frac{n+1}{n}} +\sqrt{\frac{n+2}{n}} + \cdots +\sqrt{\frac{n+n}{n}})$
19神奈川県教員採用試験(数学:6番 剰余の定理)

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
6⃣
P(x)をx+1,$(x-1)^2$で割った余りは、-3,-3x+6
P(x)を$(x+1)(x-1)^2$で割った余りを求めよ。
この動画を見る
6⃣
P(x)をx+1,$(x-1)^2$で割った余りは、-3,-3x+6
P(x)を$(x+1)(x-1)^2$で割った余りを求めよ。
18神奈川県教員採用試験(数学:5番 式変形)

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
5⃣
$x=3- \sqrt 2$
$x^4-6x^3+10x^2-13x+9$の値を求めよ。
この動画を見る
5⃣
$x=3- \sqrt 2$
$x^4-6x^3+10x^2-13x+9$の値を求めよ。
19神奈川県教員採用試験(数学:5番 三角関数)
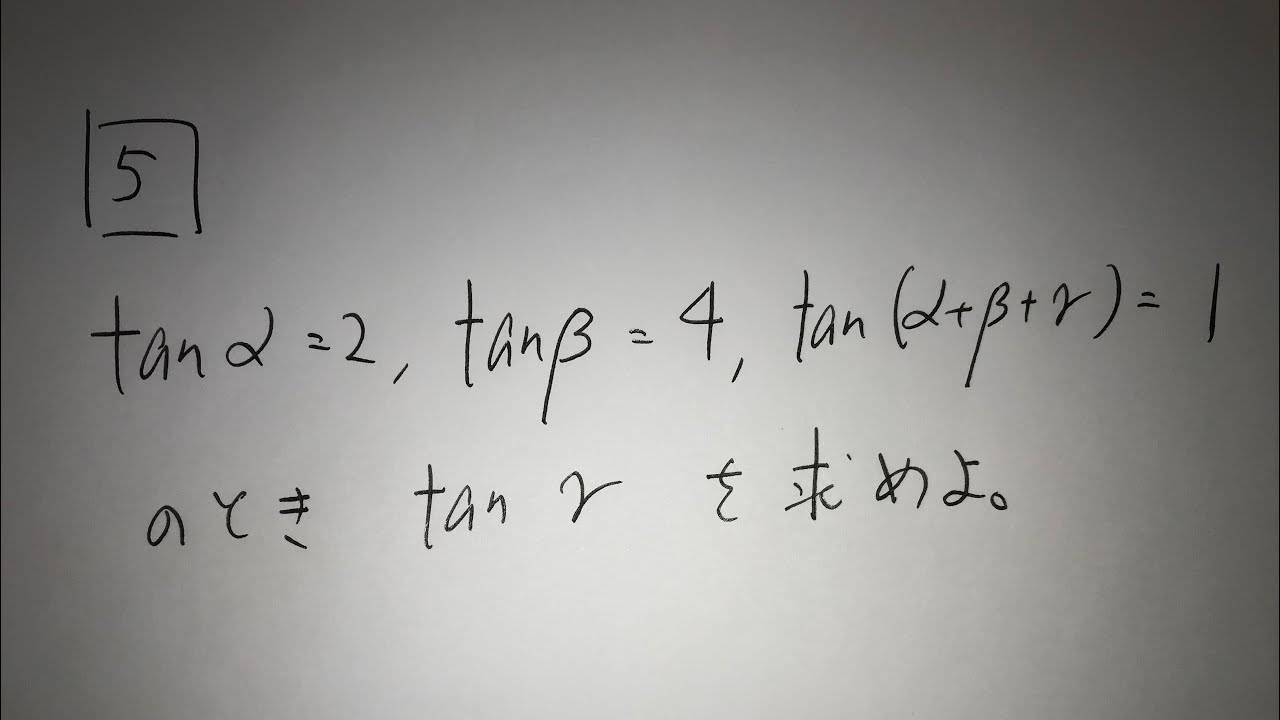
単元:
#数Ⅱ#三角関数#加法定理とその応用#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
5⃣
tanα=2,tanβ=4,tan(α+β+γ)=1のときtanγを求めよ。
この動画を見る
5⃣
tanα=2,tanβ=4,tan(α+β+γ)=1のときtanγを求めよ。
16奈良県教員採用試験(数学:高校5番 y軸回転体)

単元:
#微分とその応用#積分とその応用#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
5⃣ $l:y=x \sqrt{1-x^2}$ $(0 \leqq x \leqq 1)$
(1)極値、グラフ
(2)l、x軸で囲まれた図形をy軸を中心にした回転体の体積V
この動画を見る
5⃣ $l:y=x \sqrt{1-x^2}$ $(0 \leqq x \leqq 1)$
(1)極値、グラフ
(2)l、x軸で囲まれた図形をy軸を中心にした回転体の体積V
16東京都教員採用試験(数学:3番 微積)

単元:
#微分とその応用#積分とその応用#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
3⃣$C_1 : y=ax^2,C_2:y=logx$
$C_1$と$C_2$は共通に接線lをもつ
(1)定数aの値
(2)接線lの方程式
(3)$C_1$,l,y軸で囲まれた面積S
この動画を見る
3⃣$C_1 : y=ax^2,C_2:y=logx$
$C_1$と$C_2$は共通に接線lをもつ
(1)定数aの値
(2)接線lの方程式
(3)$C_1$,l,y軸で囲まれた面積S
14兵庫県教員採用試験(数学:1-2番 因数分解)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(2)
$(a+b+c)^3 -a^3-b^3-c^3$を因数分解せよ。
この動画を見る
1⃣-(2)
$(a+b+c)^3 -a^3-b^3-c^3$を因数分解せよ。
14兵庫県教員採用試験(数学:1-5番 解と係数の関係)

単元:
#数Ⅰ#数Ⅱ#複素数と方程式#図形と計量#三角比(三角比・拡張・相互関係・単位円)#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(5)
$8x^2+kx-3=0,x=sinθ,cosθ$のときkの値を求めよ。
この動画を見る
1⃣-(5)
$8x^2+kx-3=0,x=sinθ,cosθ$のときkの値を求めよ。
14兵庫県教員採用試験(数学:1-1番 整数問題)
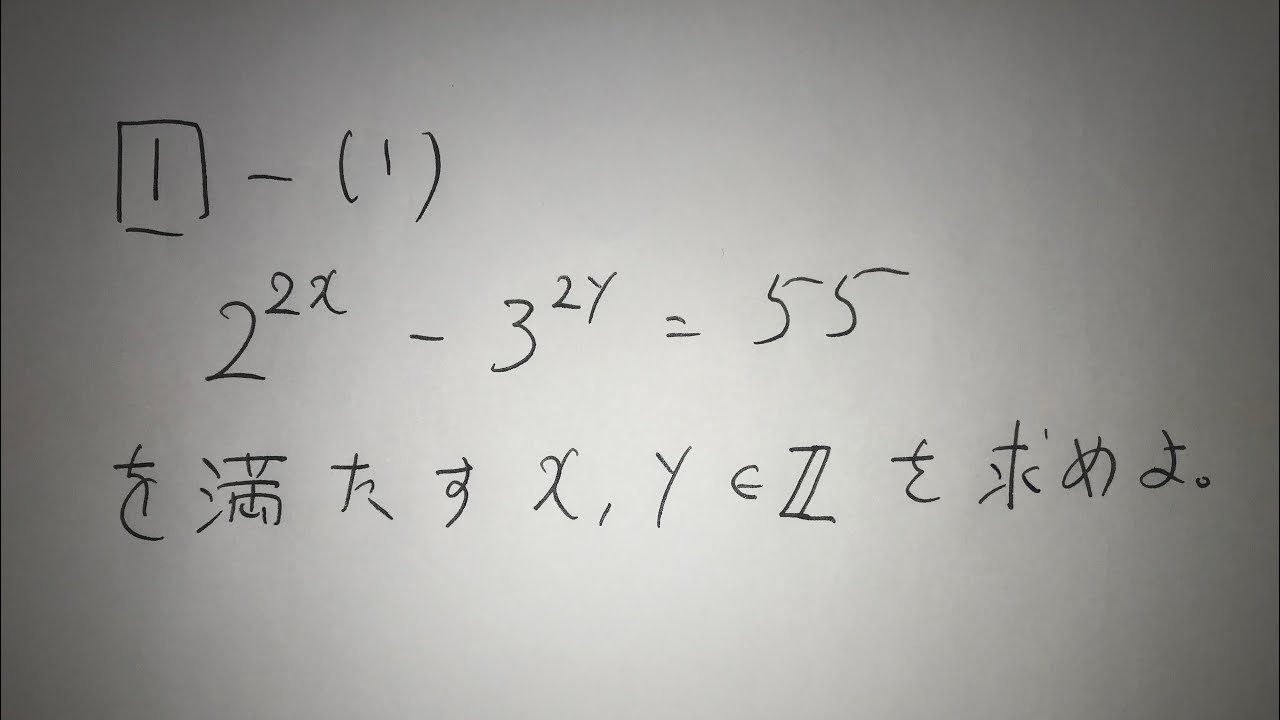
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(1)
$2^{2x}-3^{2y} =55$を満たす、$x,y \in \mathbb{ Z }$を求めよ。
この動画を見る
1⃣-(1)
$2^{2x}-3^{2y} =55$を満たす、$x,y \in \mathbb{ Z }$を求めよ。
16大阪府教員採用試験(数学:1-3番 ベクトル)

単元:
#空間ベクトル#その他#数学(高校生)#数C#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(6)
A(3,-4,5)の平面α:x+2y+z-10=0に関する対称点A'の座標を求めよ。
この動画を見る
1⃣-(6)
A(3,-4,5)の平面α:x+2y+z-10=0に関する対称点A'の座標を求めよ。
19大阪府教員採用試験(数学:2-6番 軌跡)

単元:
#数Ⅱ#図形と方程式#軌跡と領域#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣-(6)
$y=3x+1,y=-\frac{1}{3}x+2$のなす角の二等分線の直線の方程式を求めよ。
この動画を見る
2⃣-(6)
$y=3x+1,y=-\frac{1}{3}x+2$のなす角の二等分線の直線の方程式を求めよ。
16東京都教員採用試験(数学:1-5番 行列)
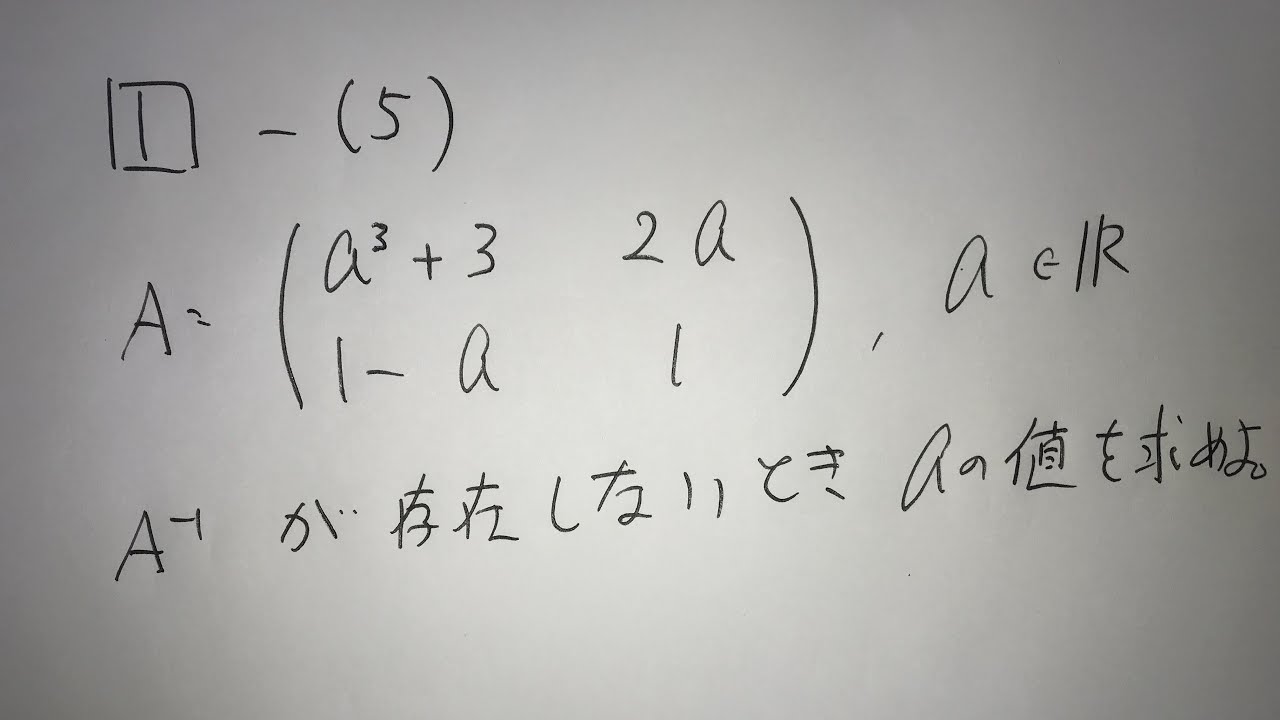
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(5)
$\begin{eqnarray}
A = \left(
\begin{array}{cccc}
a^3 & 2a \\
1-a & 1
\end{array}
\right)
\end{eqnarray}
, \quad a \in \mathbb{ R }$
$A^{-1}$が存在しないとき、aの値を求めよ。
この動画を見る
1⃣-(5)
$\begin{eqnarray}
A = \left(
\begin{array}{cccc}
a^3 & 2a \\
1-a & 1
\end{array}
\right)
\end{eqnarray}
, \quad a \in \mathbb{ R }$
$A^{-1}$が存在しないとき、aの値を求めよ。
16東京都教員採用試験(数学:1-6番 複素数)
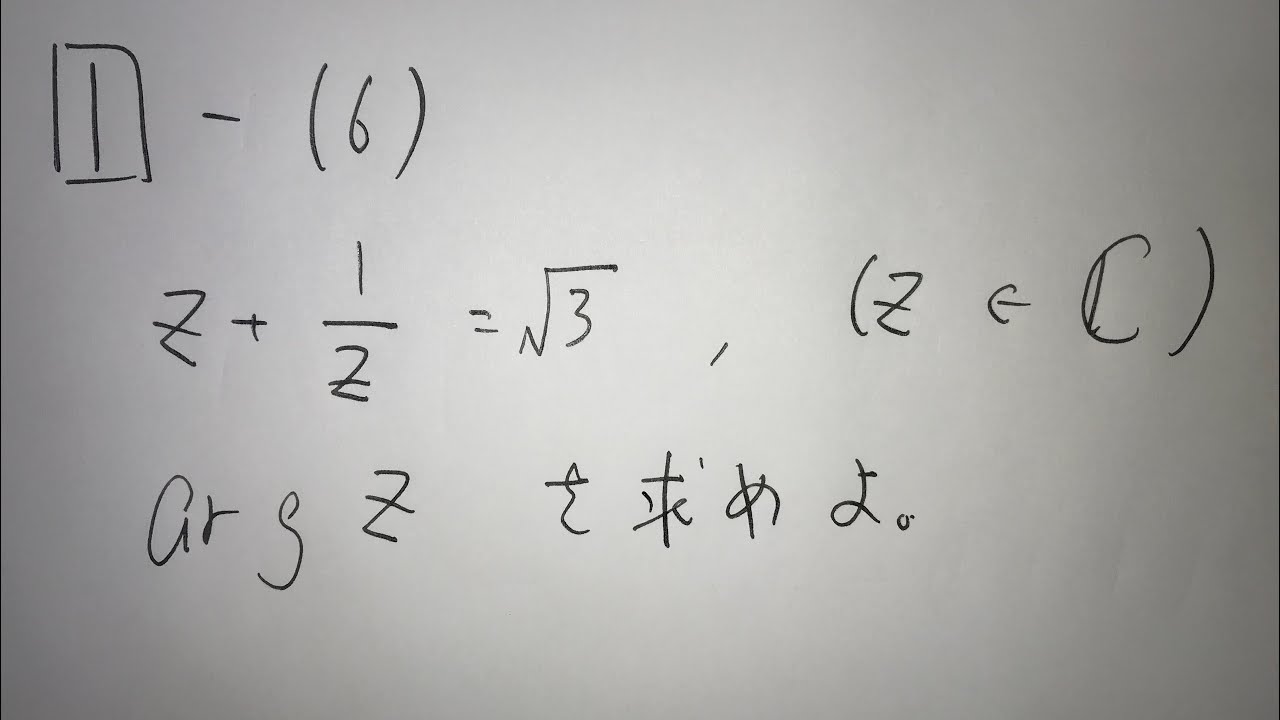
単元:
#複素数平面#複素数平面#その他#数学(高校生)#数C#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(6)
$Z+\frac{1}{Z} = \sqrt 3$ , $(Z \in \mathbb{ C })$
argZを求めよ。
この動画を見る
1⃣-(6)
$Z+\frac{1}{Z} = \sqrt 3$ , $(Z \in \mathbb{ C })$
argZを求めよ。
16東京都教員採用試験(数学:1-7 極限値)
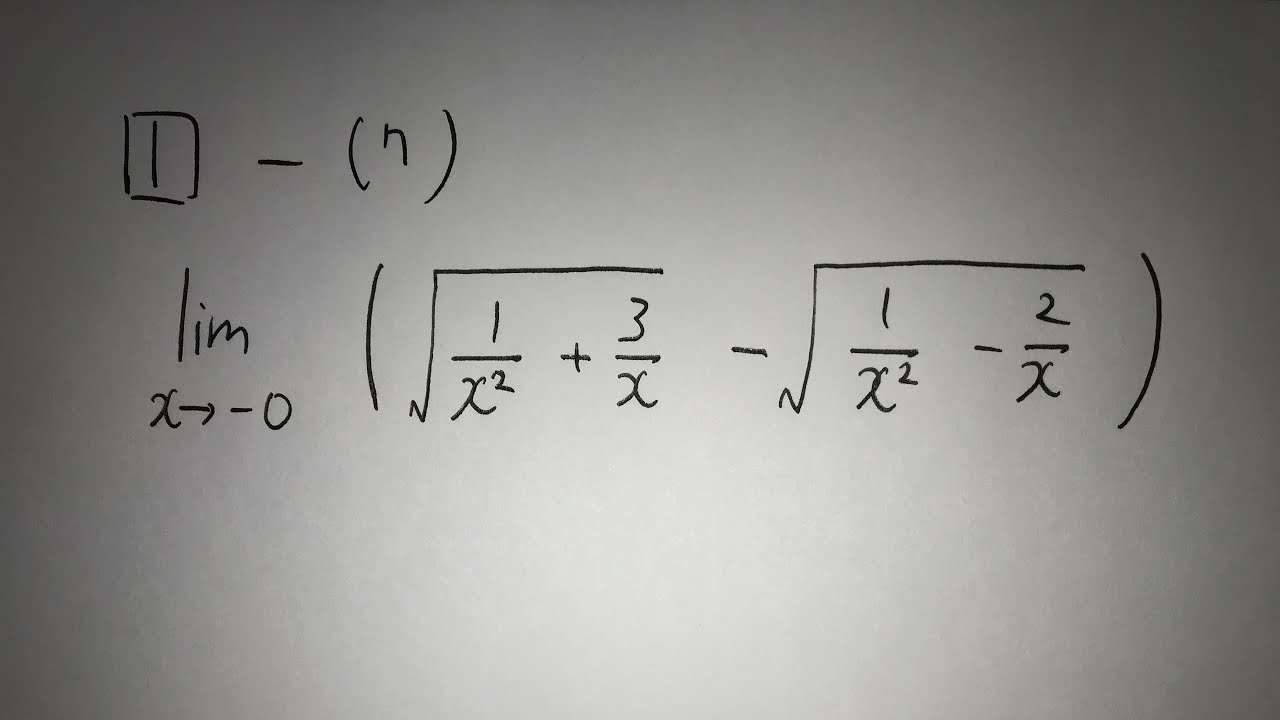
単元:
#関数と極限#関数の極限#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(7)
$\displaystyle \lim_{ n \to -0 } (\sqrt{\frac{1}{x^2}+\frac{3}{x}} - \sqrt{\frac{1}{x^2}-\frac{2}{x}})$
この動画を見る
1⃣-(7)
$\displaystyle \lim_{ n \to -0 } (\sqrt{\frac{1}{x^2}+\frac{3}{x}} - \sqrt{\frac{1}{x^2}-\frac{2}{x}})$
19京都府教員採用試験(数学:1番 複素数)
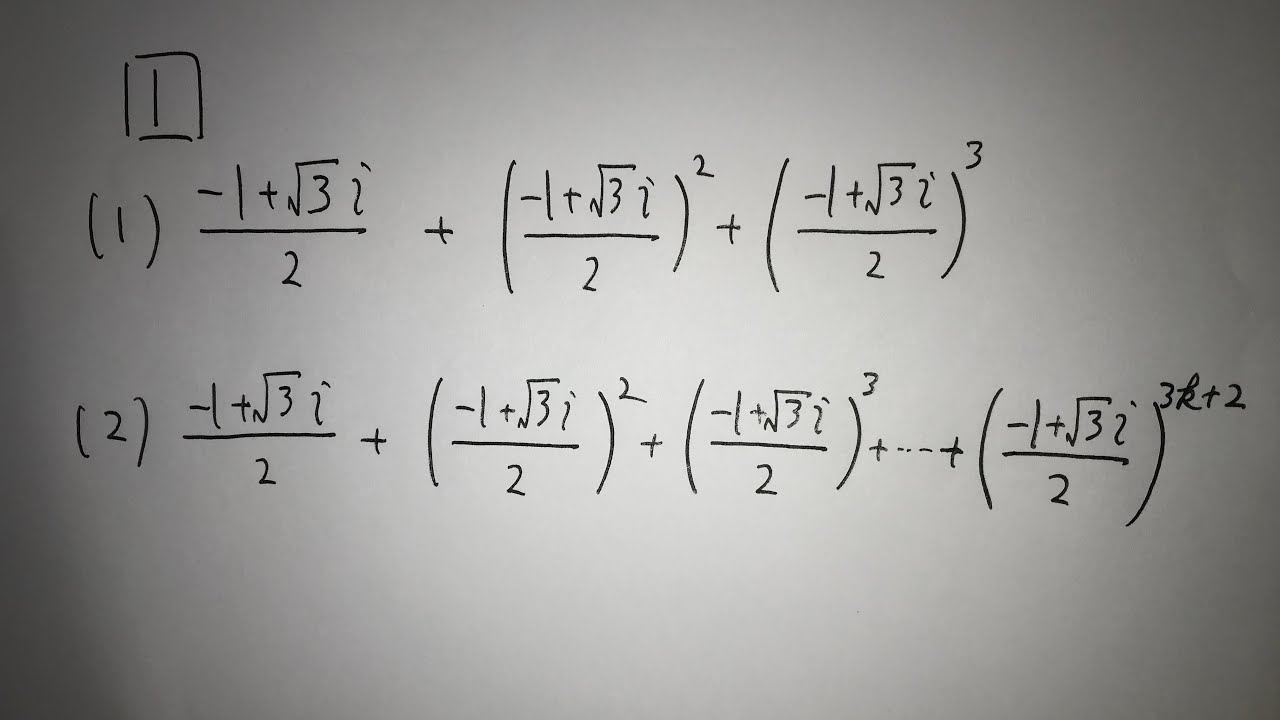
単元:
#複素数平面#複素数平面#その他#数学(高校生)#数C#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣
(1)$\frac{-1+\sqrt 3 i }{2}+(\frac{-1+\sqrt 3 i }{2})^2+(\frac{-1+\sqrt 3 i }{2})^3$
(2)$\frac{-1+\sqrt 3 i }{2}+(\frac{-1+\sqrt 3 i }{2})^2+(\frac{-1+\sqrt 3 i }{2})^3+ \cdots + (\frac{-1+\sqrt 3 i }{2})^{3k+2}$
この動画を見る
1⃣
(1)$\frac{-1+\sqrt 3 i }{2}+(\frac{-1+\sqrt 3 i }{2})^2+(\frac{-1+\sqrt 3 i }{2})^3$
(2)$\frac{-1+\sqrt 3 i }{2}+(\frac{-1+\sqrt 3 i }{2})^2+(\frac{-1+\sqrt 3 i }{2})^3+ \cdots + (\frac{-1+\sqrt 3 i }{2})^{3k+2}$
17東京都教員採用試験(数学:1-7番 シグマと極限値)
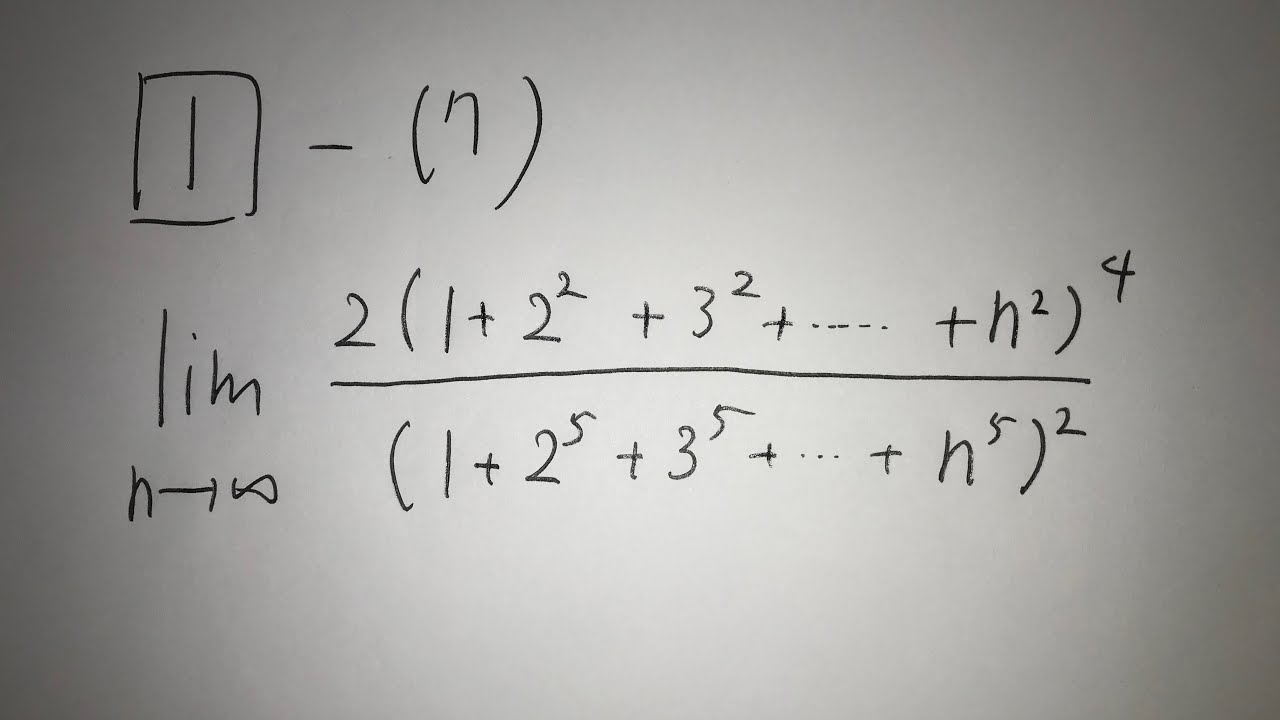
単元:
#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#その他#数学(高校生)#数B#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(7)
$\displaystyle \lim_{ n \to \infty } \frac{2(1+2^2+3^2+\cdots+n^2)^4}{(1+2^5+3^5+\cdots+n^5)^2}$
この動画を見る
1⃣-(7)
$\displaystyle \lim_{ n \to \infty } \frac{2(1+2^2+3^2+\cdots+n^2)^4}{(1+2^5+3^5+\cdots+n^5)^2}$
19大阪府教員採用試験(数学:2-7番 数列)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣-(7)
a<b<c , b>0
a,b,cの順で等差数列、$a^2,b^2,c^2$の順で等比数列のとき公比rを求めよ。
この動画を見る
2⃣-(7)
a<b<c , b>0
a,b,cの順で等差数列、$a^2,b^2,c^2$の順で等比数列のとき公比rを求めよ。
17兵庫県教員採用試験(数学:3番 微積)

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#接線と増減表・最大値・最小値#その他#不定積分・定積分#面積、体積#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
3⃣
$l_1:y=kx+2k$ $(k \in \mathbb{ R })$
$l_2:y=x^3-3x+2$
(1)$l_2$の極値
(2)k=0,$l_1$と$l_2$で囲まれた面積
(3)$l_1$と$l_2$が3点で交わるkの範囲
(4)$l_1$が$l_2$の変曲点を通るとき$l_1$と$l_2$で囲まれた面積
この動画を見る
3⃣
$l_1:y=kx+2k$ $(k \in \mathbb{ R })$
$l_2:y=x^3-3x+2$
(1)$l_2$の極値
(2)k=0,$l_1$と$l_2$で囲まれた面積
(3)$l_1$と$l_2$が3点で交わるkの範囲
(4)$l_1$が$l_2$の変曲点を通るとき$l_1$と$l_2$で囲まれた面積
17兵庫県教員採用試験(数学:1-1 場合の下図)

単元:
#数A#場合の数と確率#場合の数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(1)
3つの頂点で△を作る。
(1)△は全部で何個
(2)3つの辺が全て異なる△の個数
*図は動画内参照
この動画を見る
1⃣-(1)
3つの頂点で△を作る。
(1)△は全部で何個
(2)3つの辺が全て異なる△の個数
*図は動画内参照
17兵庫県教員採用試験(数学:1-2番 不等式)

単元:
#2次関数#2次方程式と2次不等式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(2)
$x^2-(2a+3)x+6a<0$を満たす整数解が3つとなるaの範囲
この動画を見る
1⃣-(2)
$x^2-(2a+3)x+6a<0$を満たす整数解が3つとなるaの範囲
17兵庫県教員採用試験(数学:1-3番 剰余の定理)
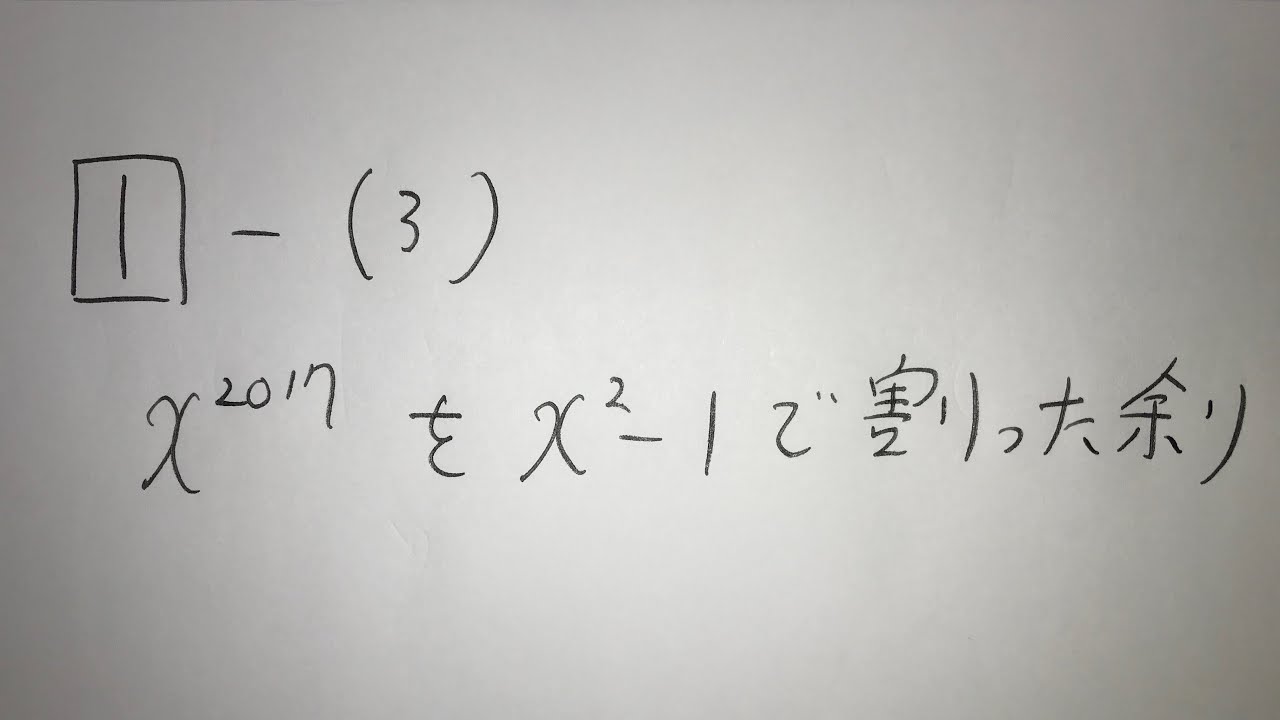
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(3)
$x^{2017}$を$x^2-1$で割った余り
この動画を見る
1⃣-(3)
$x^{2017}$を$x^2-1$で割った余り
19兵庫県教員採用試験(数学:1-3番 命題)
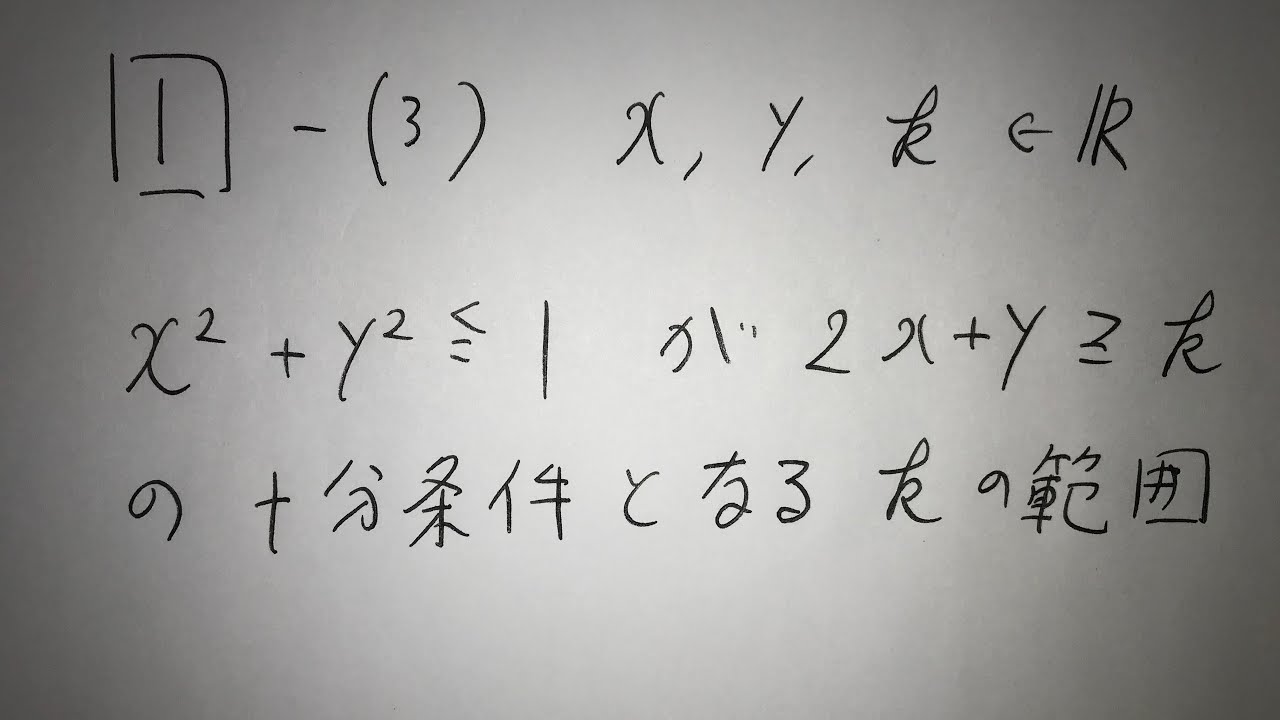
単元:
#数Ⅰ#数Ⅱ#数と式#集合と命題(集合・命題と条件・背理法)#図形と方程式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(3)
$x,y,k \in \mathbb{ R }$
$x^2+y^2 \leqq 1$が$2x+y \geqq k$の十分条件となるkの範囲
この動画を見る
1⃣-(3)
$x,y,k \in \mathbb{ R }$
$x^2+y^2 \leqq 1$が$2x+y \geqq k$の十分条件となるkの範囲



