 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【高校物理】【プランク定数】図は、陰極にタングステンを利用し、光電管に入射する光の振動数νを変化させて,光電子の最大運動エネルギー Kmを測定した結果である。(1) タングステンの仕事関数はいくらか…

単元:
#物理#理科(高校生)#原子
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
図は、陰極にタングステンを利用し、光電管に入射する光の振動数νを変化させて,光電子の最大運動エネルギー Kmを測定した結果である。
(1) タングステンの仕事関数はいくらか。
(2) プランク定数はいくらか。グラフから求めよ。
この動画を見る
図は、陰極にタングステンを利用し、光電管に入射する光の振動数νを変化させて,光電子の最大運動エネルギー Kmを測定した結果である。
(1) タングステンの仕事関数はいくらか。
(2) プランク定数はいくらか。グラフから求めよ。
【受験算数】ニュートン算:途中で牛の数を変えると草はどうなる?

単元:
#算数(中学受験)#文章題#仕事算とニュートン算
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
大問1
現在一定の草が生えている牧場では、100頭の牛を放すと48週間で食べつくしてしまい、125頭の牛を放すと36週間で食べつくしてしまいます。草は毎日一定の割合ではえ、牛はどの牛も1日に同じ量だけ草を食べるものとして、次の問いに答えなさい。
(1) 牛1頭が1週間に食べる草の量を1山とすると、1週間につき何山この牧場には草がはえますか。
(2) この牧場で牛200頭を8週間放した後、ちょうど22週間食べさせるためには、 牛を何頭にすればよいですか。
大問2
現在一定の草が生えている牧場では、100頭の牛を放すと18週間で食べつくしてしまい、91頭の牛を放すと20週間で食べつくしてしまいます。草は毎日一定の割合ではえ、牛はどの牛も1日に同じ量だけ草を食べるものとして、次の問いに答えなさい。
(1) 牛1頭が1週間に食べる草の量を1山とすると、1週間につき何山この牧場 には草がはえますか。
(2) この牧場で牛70頭を5週間放した後、ちょうど33週間食べさせるためには、牛を何頭にすればよいですか。
この動画を見る
大問1
現在一定の草が生えている牧場では、100頭の牛を放すと48週間で食べつくしてしまい、125頭の牛を放すと36週間で食べつくしてしまいます。草は毎日一定の割合ではえ、牛はどの牛も1日に同じ量だけ草を食べるものとして、次の問いに答えなさい。
(1) 牛1頭が1週間に食べる草の量を1山とすると、1週間につき何山この牧場には草がはえますか。
(2) この牧場で牛200頭を8週間放した後、ちょうど22週間食べさせるためには、 牛を何頭にすればよいですか。
大問2
現在一定の草が生えている牧場では、100頭の牛を放すと18週間で食べつくしてしまい、91頭の牛を放すと20週間で食べつくしてしまいます。草は毎日一定の割合ではえ、牛はどの牛も1日に同じ量だけ草を食べるものとして、次の問いに答えなさい。
(1) 牛1頭が1週間に食べる草の量を1山とすると、1週間につき何山この牧場 には草がはえますか。
(2) この牧場で牛70頭を5週間放した後、ちょうど33週間食べさせるためには、牛を何頭にすればよいですか。
【数Ⅲ】【関数と極限】初項1、公比1/7の無限等比級数の和Sと、初項から第n項までの部分和Snとの差が、初めて1/1000より小さくなるようなnの値を求めよ。

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
初項1、公比1/7の無限等比級数の和Sと、初項から第n項までの部分和Snとの差が、
初めて1/1000より小さくなるようなnの値を求めよ。
この動画を見る
初項1、公比1/7の無限等比級数の和Sと、初項から第n項までの部分和Snとの差が、
初めて1/1000より小さくなるようなnの値を求めよ。
【数Ⅲ】【関数と極限】第2項が3である無限等比級数が収束し、その和が-4であるとき、初項と公比を求めよ。

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
第2項が3である無限等比級数が収束し、その和が-4であるとき、初項と公比を求めよ。
この動画を見る
第2項が3である無限等比級数が収束し、その和が-4であるとき、初項と公比を求めよ。
【数Ⅲ】【関数と極限】a₁=1/35、1/an+₁=1/an +8n+20によって定められる数列{an}について、次の問いに答えよ。(1) anをnの式で表せ。(2) 無限級数Σanの和を求めよ。

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
数列 $\{a_n\}$ は以下のように定められる数列について、次の問いに答えよ
$a_1 = \frac{1}{35}$,$\quad \frac{1}{a_{n+1}} = \frac{1}{a_n} + 8n + 20 \quad$ $(n = 1, 2, 3, \ldots)$
(1)$a_n$を$n$ の式で表せ。
(2)無限級数 $\displaystyle \sum_{n=1}^{\infty} a_n$ の和を求めよ。
この動画を見る
数列 $\{a_n\}$ は以下のように定められる数列について、次の問いに答えよ
$a_1 = \frac{1}{35}$,$\quad \frac{1}{a_{n+1}} = \frac{1}{a_n} + 8n + 20 \quad$ $(n = 1, 2, 3, \ldots)$
(1)$a_n$を$n$ の式で表せ。
(2)無限級数 $\displaystyle \sum_{n=1}^{\infty} a_n$ の和を求めよ。
【中学受験理科】【中和②】いくつかの蒸発皿に、塩酸Aを 20㎤ずつ入れ、いろいろな体積の水酸化ナトリウム水溶液Bを加えました。グラフは、AとBを混ぜたあとに水分を蒸発させ、残った固体の重さをまとめた…

単元:
#理科(中学受験)#化学分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
いくつかの蒸発皿に、塩酸Aを 20㎤ずつ入れ、いろいろな体積の水酸化ナトリウム水溶液Bを加えました。グラフは、AとBを混ぜたあとに水分を蒸発させ、残った固体の重さをまとめたものです。
問1
A 10㎤を完全に中和するためには、Bは何 ㎤必要ですか。
問2
Bを30㎤加えたとき、残った固体の中に塩化ナトリウムと水酸化ナトリウムはそれぞれ何gずつありますか。
問3
Bを50㎤加えたとき、残った固体の中に塩化ナトリウムと水酸化ナトリウムはそれぞれ何gずつありますか。
問4
A 40㎤とB 100㎤を混ぜたあとに水分を蒸発させたとき、残った固体の中に塩化ナトリウムと水酸化ナトリウムはそれぞれ何gずつありますか。
この動画を見る
いくつかの蒸発皿に、塩酸Aを 20㎤ずつ入れ、いろいろな体積の水酸化ナトリウム水溶液Bを加えました。グラフは、AとBを混ぜたあとに水分を蒸発させ、残った固体の重さをまとめたものです。
問1
A 10㎤を完全に中和するためには、Bは何 ㎤必要ですか。
問2
Bを30㎤加えたとき、残った固体の中に塩化ナトリウムと水酸化ナトリウムはそれぞれ何gずつありますか。
問3
Bを50㎤加えたとき、残った固体の中に塩化ナトリウムと水酸化ナトリウムはそれぞれ何gずつありますか。
問4
A 40㎤とB 100㎤を混ぜたあとに水分を蒸発させたとき、残った固体の中に塩化ナトリウムと水酸化ナトリウムはそれぞれ何gずつありますか。
【高校化学】【二置換体の構造異性体】芳香族化合物 Aは炭素, 水素、酸素からなり,ベンゼン環に2つの置換基が結合している。 化合物Aのベンゼン環の水素原子のうち1つを塩素原子で置き換えた化合物は2種…

単元:
#化学#有機#有機化合物の特徴と構造#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
芳香族化合物 Aは炭素, 水素、酸素からなり,ベンゼン環に2つの置換基が結合している。 化合物Aのベンゼン環の水素原子のうち1つを塩素原子で置き換えた化合物は2種類存在する。 化合物Aの分子量は200以下であることがわかっている。221mg の化合物Aを完全燃焼させると, 572mgの二酸化炭素と117mg の水が生成した。化合物Aに塩化鉄(Ⅲ) 水溶液を加えると, 紫色の呈色があった。化合物Aにヨウ素と水酸化ナトリウム水溶液を加えて温めると, 特有の臭いをもつ①黄色沈殿が生じた。
芳香族化合物BおよびCはいずれも化合物Aの構造異性体であり、ベンゼン環に2つの置換基が結合している。 ②化合物Bに炭酸水素ナトリウム水溶液を加えると、二酸化炭素が発生した。化合物Cにアンモニア性硝酸銀水溶液を加えて温めると, 銀が析出した。化合物Cに塩化鉄(III) 水溶液を加えても呈色はなかった。化合物BおよびCそれぞれを, 過マンガン酸カリウム水溶液で酸化すると,いずれの場合も二価カルボン酸であるDが得られた。 化合物Dのベンゼン環の水素原子のうち1つを塩素原子で置き換えた化合物は3種類存在する。
(1) 化合物Aの分子式を記せ。
(2)①の化合物の分子式を記せ。
(3)化合物 A, C, D の構造式をそれぞれ記せ。
(4)②について, 構造式を使ってその化学反応式を記せ。
この動画を見る
芳香族化合物 Aは炭素, 水素、酸素からなり,ベンゼン環に2つの置換基が結合している。 化合物Aのベンゼン環の水素原子のうち1つを塩素原子で置き換えた化合物は2種類存在する。 化合物Aの分子量は200以下であることがわかっている。221mg の化合物Aを完全燃焼させると, 572mgの二酸化炭素と117mg の水が生成した。化合物Aに塩化鉄(Ⅲ) 水溶液を加えると, 紫色の呈色があった。化合物Aにヨウ素と水酸化ナトリウム水溶液を加えて温めると, 特有の臭いをもつ①黄色沈殿が生じた。
芳香族化合物BおよびCはいずれも化合物Aの構造異性体であり、ベンゼン環に2つの置換基が結合している。 ②化合物Bに炭酸水素ナトリウム水溶液を加えると、二酸化炭素が発生した。化合物Cにアンモニア性硝酸銀水溶液を加えて温めると, 銀が析出した。化合物Cに塩化鉄(III) 水溶液を加えても呈色はなかった。化合物BおよびCそれぞれを, 過マンガン酸カリウム水溶液で酸化すると,いずれの場合も二価カルボン酸であるDが得られた。 化合物Dのベンゼン環の水素原子のうち1つを塩素原子で置き換えた化合物は3種類存在する。
(1) 化合物Aの分子式を記せ。
(2)①の化合物の分子式を記せ。
(3)化合物 A, C, D の構造式をそれぞれ記せ。
(4)②について, 構造式を使ってその化学反応式を記せ。
【受験算数】ニュートン算:駐車場の車の台数

単元:
#算数(中学受験)#文章題#仕事算とニュートン算
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
大問1
ある駐車場に、午後2時に何台かの車が入っていて、しかも、毎分一定の割合で車が入ってきます。いま、3分間に2台の割合で車が出ていくと、午後6時48分に駐車場の車はなくなり、4分間に3台の割合で車が出ていくと、午後5時12分に駐車場の車はすっかりなくなります。
(1)午後2時に駐車していた車の台数を求めなさい。
(2)6分間に5台の割合で車が出ていくとき、午後何時何分に駐車場に車がいなくなりますか。
大問2
ある駐車場に、午後2時に何台かの車が入っていて、しかも、毎分一定の割合で車が入ってきます。いま、3分間に2台の割合で車が出ていくと、午後6時30分に駐車場の車はなくなり、8分間に5台の割合で車が出ていくと、午後7時20分に駐車場の車はすっかりなくなります。
(1)午後2時に駐車していた車の台数を求めなさい。
(2)7分間に4台の割合で車が出ていくとき、午後何時何分に駐車場に車がいなくなりますか。
この動画を見る
大問1
ある駐車場に、午後2時に何台かの車が入っていて、しかも、毎分一定の割合で車が入ってきます。いま、3分間に2台の割合で車が出ていくと、午後6時48分に駐車場の車はなくなり、4分間に3台の割合で車が出ていくと、午後5時12分に駐車場の車はすっかりなくなります。
(1)午後2時に駐車していた車の台数を求めなさい。
(2)6分間に5台の割合で車が出ていくとき、午後何時何分に駐車場に車がいなくなりますか。
大問2
ある駐車場に、午後2時に何台かの車が入っていて、しかも、毎分一定の割合で車が入ってきます。いま、3分間に2台の割合で車が出ていくと、午後6時30分に駐車場の車はなくなり、8分間に5台の割合で車が出ていくと、午後7時20分に駐車場の車はすっかりなくなります。
(1)午後2時に駐車していた車の台数を求めなさい。
(2)7分間に4台の割合で車が出ていくとき、午後何時何分に駐車場に車がいなくなりますか。
【数Ⅲ】【関数と極限】次の無限級数の収束、発散について調べ、収束する場合は、その和を求めよ。(1) 2 + 2/1+2 + 2/1+2+3 +・・・+ 2/1+2+3+…+n +・・・他

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の無限級数の収束・発散について調べ,収束する場合はその和を求めよ。
(1)$2+\frac{2}{1+2} + \frac{2}{1+2+3} + \frac{2}{1+2+3+4} + \cdots$
(2)$\frac{1}{3} + \frac{1}{3+5} + \frac{1}{3+5+7} + \cdots + \frac{1}{3+5+7+\cdots+(2n+1)} + \cdots$
この動画を見る
次の無限級数の収束・発散について調べ,収束する場合はその和を求めよ。
(1)$2+\frac{2}{1+2} + \frac{2}{1+2+3} + \frac{2}{1+2+3+4} + \cdots$
(2)$\frac{1}{3} + \frac{1}{3+5} + \frac{1}{3+5+7} + \cdots + \frac{1}{3+5+7+\cdots+(2n+1)} + \cdots$
【高校物理】【磁場中での放射線の進路】図のように、真空中に放射線源と磁石を配置した。次の(1)~(3)の放射線が、放射線源から鉛直上向きに飛び出したとすると、どのような進路となるか。図の(a)~(c…

単元:
#物理#理科(高校生)#原子
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、真空中に放射線源と磁石を配置した。次の(1)~(3)の放射線が、放射線源から鉛直上向きに飛び出したとすると、どのような進路となるか。図の(a)~(c) の中から適切なものを選び、理由とともに記号で答えよ。
この動画を見る
図のように、真空中に放射線源と磁石を配置した。次の(1)~(3)の放射線が、放射線源から鉛直上向きに飛び出したとすると、どのような進路となるか。図の(a)~(c) の中から適切なものを選び、理由とともに記号で答えよ。
【受験算数】くるった時計(発展)A君の時計は何時をさしている?

単元:
#算数(中学受験)#速さ#点の移動・時計算#速さその他
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
大問1
A君とB君の2人は新幹線に乗りました。東京駅をちょうど14時に出発した列車が博多駅に到着しました。列車がプラットホームに止まった瞬間、A君の時計は19 時0分を、B君の時計は18時0分をさしていました。A、B両君の時計でわかっていることは、次の①、②、③の3つです。
① B君の時計はその日の12時の時報に合っていました。
② A君の時計はその日の16時の時報に合っていました。
③ A, B両君は、その日、2人の時計が同時に10時0分をさしているのを互いに確かめました。
このとき、次の問いに答えなさい。
(1) 正しい時計が12時をさしているとき、A君の時計は何時何分をさしていますか。
(2) この列車が出発してから到着するまでにかかった時間は何時間何分ですか。
大問2
A君とB君の2人は東北新幹線に乗りました。東京駅をちょうど14時に出発した列車が八戸駅に到着しました。列車がプラットホームに止まった瞬間、A君の時計は18 時0分を、B君の時計は16時0分をさしていました。A、B両君の時計でわかっていることは、次の①、②、③の3つです。
① A君の時計は前の日の22時の時報に合わせました。
② B君の時計はその日の10時の時報に合っていました。
③ A, B両君は、その日、2人の時計が同時に8時0分をさしているのを互いに確かめました。
このとき、次の問いに答えなさい。
(1) 正しい時計が10時をさしているとき、A君の時計は何時何分をさしていますか。
(2) この列車が出発してから到着するまでにかかった時間は何時間何分ですか。
この動画を見る
大問1
A君とB君の2人は新幹線に乗りました。東京駅をちょうど14時に出発した列車が博多駅に到着しました。列車がプラットホームに止まった瞬間、A君の時計は19 時0分を、B君の時計は18時0分をさしていました。A、B両君の時計でわかっていることは、次の①、②、③の3つです。
① B君の時計はその日の12時の時報に合っていました。
② A君の時計はその日の16時の時報に合っていました。
③ A, B両君は、その日、2人の時計が同時に10時0分をさしているのを互いに確かめました。
このとき、次の問いに答えなさい。
(1) 正しい時計が12時をさしているとき、A君の時計は何時何分をさしていますか。
(2) この列車が出発してから到着するまでにかかった時間は何時間何分ですか。
大問2
A君とB君の2人は東北新幹線に乗りました。東京駅をちょうど14時に出発した列車が八戸駅に到着しました。列車がプラットホームに止まった瞬間、A君の時計は18 時0分を、B君の時計は16時0分をさしていました。A、B両君の時計でわかっていることは、次の①、②、③の3つです。
① A君の時計は前の日の22時の時報に合わせました。
② B君の時計はその日の10時の時報に合っていました。
③ A, B両君は、その日、2人の時計が同時に8時0分をさしているのを互いに確かめました。
このとき、次の問いに答えなさい。
(1) 正しい時計が10時をさしているとき、A君の時計は何時何分をさしていますか。
(2) この列車が出発してから到着するまでにかかった時間は何時間何分ですか。
【英語】動詞の時制を選ぼう!時制英文法問題解説1!

単元:
#英語(高校生)#英文法#時制
指導講師:
理数個別チャンネル
問題文全文(内容文):
時制英文法問題
You were foolish to play football on such a hot day.
It was careless of them to forget their water bottles.
It is kind of you to help me with my report.
Meg has decided not to stay up late.
She studied hard in order not to fail the math test.
Take care not to catch a cold before the test.
この動画を見る
時制英文法問題
You were foolish to play football on such a hot day.
It was careless of them to forget their water bottles.
It is kind of you to help me with my report.
Meg has decided not to stay up late.
She studied hard in order not to fail the math test.
Take care not to catch a cold before the test.
【数Ⅲ】【関数と極限】nは自然数とし、h>0のとき、不等式(1+h)^n≧1+nh+n(n-1)/2・h²が成り立つ。このことを用いて、数列{n/3^n}の極限を求めよ。

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
nは自然数とし、h>0のとき、
不等式$(1+h)^n≧1+nh+\dfrac{n(n-1)}{2}・h²$が成り立つ。
このことを用いて、数列$\dfrac{n}{3^n}$の極限を求めよ。
この動画を見る
nは自然数とし、h>0のとき、
不等式$(1+h)^n≧1+nh+\dfrac{n(n-1)}{2}・h²$が成り立つ。
このことを用いて、数列$\dfrac{n}{3^n}$の極限を求めよ。
【数Ⅲ】【関数と極限】次の条件によって定められる数列{an}の極限を求めよ。a₁=0、a₂=1、3an+₂=an+₁+2an他

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の条件によって定められる数列$a_n$の極限を求めよ。
(1) $a₁=0$、$a₂=1$、$3a_{n+2}=a_{n+1}+2a_n$
(2) $a₁=0$、$a₂=1$、$a_{n+2}-7a_{n+1}+10a_n=0$
(3) $a₁=1$、$a₂=2$、$a_{n+2}-6a_{n+1}+9a_n=0$
この動画を見る
次の条件によって定められる数列$a_n$の極限を求めよ。
(1) $a₁=0$、$a₂=1$、$3a_{n+2}=a_{n+1}+2a_n$
(2) $a₁=0$、$a₂=1$、$a_{n+2}-7a_{n+1}+10a_n=0$
(3) $a₁=1$、$a₂=2$、$a_{n+2}-6a_{n+1}+9a_n=0$
【受験算数】花子の時計は1日に正しい時計より40分進み、和子の時計は1日に30分おくれます。ある日の正午に、2人の時計を正しい時刻に合わせました。その日の午後7時30分に和子の時計は何時何分?

単元:
#算数(中学受験)#速さ#点の移動・時計算#速さその他
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
大問1
花子の時計は1日に正しい時計より40分進み、和子の時計は1日に30分おくれます。ある日の正午に、2人の時計を正しい時刻に合わせました。次の問いに答えなさい。ただし、答えが整数にならないときは分数で答えなさい。
(1) その日の午後7時30分に和子の時計は何時何分をさしていますか。
(2) その日の午後、花子の時計が10時をさしているとき、正しい時刻は何時何分ですか。
大問2
花子の時計は1日に正しい時計より10分おくれ、和子の時計は1日に15分進みます。ある日の正午に、2人の時計を正しい時刻に合わせました。次の問いに答えなさい。ただし、答えが整数にならないときは分数で答えなさい。
(1) その日の午後9時30分に和子の時計は何時何分をさしていますか。
(2) その日の午後、花子の時計が5時をさしているとき、正しい時刻は何時何分ですか。
この動画を見る
大問1
花子の時計は1日に正しい時計より40分進み、和子の時計は1日に30分おくれます。ある日の正午に、2人の時計を正しい時刻に合わせました。次の問いに答えなさい。ただし、答えが整数にならないときは分数で答えなさい。
(1) その日の午後7時30分に和子の時計は何時何分をさしていますか。
(2) その日の午後、花子の時計が10時をさしているとき、正しい時刻は何時何分ですか。
大問2
花子の時計は1日に正しい時計より10分おくれ、和子の時計は1日に15分進みます。ある日の正午に、2人の時計を正しい時刻に合わせました。次の問いに答えなさい。ただし、答えが整数にならないときは分数で答えなさい。
(1) その日の午後9時30分に和子の時計は何時何分をさしていますか。
(2) その日の午後、花子の時計が5時をさしているとき、正しい時刻は何時何分ですか。
【高校化学】【ベンゼンの反応】ベンゼンの反応図に示したベンゼンの反応について、次の各問いに答えよ。(図は本編中) (1) A~Dにあてはまる有機化合物の示性式と名称を記せ。 (2) (ア)~(エ)に…

単元:
#化学#有機#有機化合物の特徴と構造#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
ベンゼンの反応図に示したベンゼンの反応について、次の各問いに答えよ。(図は本編中)
(1) A~Dにあてはまる有機化合物の示性式と名称を記せ。
(2) (ア)~(エ)にあてはまる反応名を記せ。
この動画を見る
ベンゼンの反応図に示したベンゼンの反応について、次の各問いに答えよ。(図は本編中)
(1) A~Dにあてはまる有機化合物の示性式と名称を記せ。
(2) (ア)~(エ)にあてはまる反応名を記せ。
【受験算数】速さ:到着しながら休む点の問題 点Pと点Qが出会うのは、出発してから何秒後?

単元:
#算数(中学受験)#速さ#ダイヤグラム#点の移動・時計算
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
大問1
右の図のように直線上に2つの点A,Bがあり、点Pと点Qが同時に点Aを出発してAB間を往復します。ただし、点A、点Bに到着するごとに、点Pは5秒間、点Qは3秒間休みます。ABの長さが90cm、点P、点Qの速さがそれぞれ毎秒6cm、毎秒4cmのとき、次の問いに答えなさい。
(1)点P、点Qが出発してからはじめて出会うのは何秒後ですか。
(2)点Pが点Aにはじめてもどったとき、点Qは点Aから何cmのところにいますか。
(3)点P、点Qが2度目に出会うのは、出発してから何秒後ですか。また、それは、点Aから何cmのところですか。
大問2
右の図のように直線上に2つの点A,Bがあり、点Pと点Qが同時に点Aを出発してAB間を往復します。ただし、点A、点Bに到着するごとに、点Pは10秒間、点Qは4秒間休みます。ABの長さが360cm、点P、点Qの速さがそれぞれ毎秒8cm、毎秒3cmのとき、次の問いに答えなさい。
(1)点P、点Qが出発してからはじめて出会うのは何秒後ですか。
(2)点Pが点Bに2度目に到着したとき、点Qは点Bから何cmのところにいますか。
(3)点P、点Qが2度目に出会うのは、出発してから何秒後ですか。また、それは、点Bから何cmのところですか。
この動画を見る
大問1
右の図のように直線上に2つの点A,Bがあり、点Pと点Qが同時に点Aを出発してAB間を往復します。ただし、点A、点Bに到着するごとに、点Pは5秒間、点Qは3秒間休みます。ABの長さが90cm、点P、点Qの速さがそれぞれ毎秒6cm、毎秒4cmのとき、次の問いに答えなさい。
(1)点P、点Qが出発してからはじめて出会うのは何秒後ですか。
(2)点Pが点Aにはじめてもどったとき、点Qは点Aから何cmのところにいますか。
(3)点P、点Qが2度目に出会うのは、出発してから何秒後ですか。また、それは、点Aから何cmのところですか。
大問2
右の図のように直線上に2つの点A,Bがあり、点Pと点Qが同時に点Aを出発してAB間を往復します。ただし、点A、点Bに到着するごとに、点Pは10秒間、点Qは4秒間休みます。ABの長さが360cm、点P、点Qの速さがそれぞれ毎秒8cm、毎秒3cmのとき、次の問いに答えなさい。
(1)点P、点Qが出発してからはじめて出会うのは何秒後ですか。
(2)点Pが点Bに2度目に到着したとき、点Qは点Bから何cmのところにいますか。
(3)点P、点Qが2度目に出会うのは、出発してから何秒後ですか。また、それは、点Bから何cmのところですか。
【数Ⅲ】【積分とその応用】点Pの座標(x,y)が 3x=t³+6t², 3y=2t³-3t²(1)点Pが座標(27,9)を通るときの速度を求めよ(2)点Pが時刻0からaまでに通過する道のりLを求めよ。

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
点Pの座標(x,y)が、時刻の関数として次のように表されている。
3x=t³+6t², 3y=2t³-3t²
(1)点Pが座標(27,9)を通るときの速度を求めよ。
(2)点Pが時刻0からa(a>0)までに通過する道のりLを求めよ。
この動画を見る
点Pの座標(x,y)が、時刻の関数として次のように表されている。
3x=t³+6t², 3y=2t³-3t²
(1)点Pが座標(27,9)を通るときの速度を求めよ。
(2)点Pが時刻0からa(a>0)までに通過する道のりLを求めよ。
【数Ⅲ】【積分とその応用】t秒後の速度が v=30-10t(m/s)となるように地上から真上に投げ上げられた物体は、何秒後に何mの高さまで上がって落ち始めるか。

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
t秒後の速度が v=30-10t(m/s)となるように地上から真上に投げ上げられた物体は、何秒後に何mの高さまで上がって落ち始めるか。
この動画を見る
t秒後の速度が v=30-10t(m/s)となるように地上から真上に投げ上げられた物体は、何秒後に何mの高さまで上がって落ち始めるか。
【数Ⅲ】【積分とその応用】曲線x=θcosθ、y=θsinθ(0≦θ≦2π)の長さは、曲線y=x²/2(0≦θ≦2π)の長さに等しいことを示せ。

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
曲線x=θcosθ、y=θsinθ(0≦θ≦2π)の長さは、曲線y=x²/2(0≦θ≦2π)の長さに等しいことを示せ。
この動画を見る
曲線x=θcosθ、y=θsinθ(0≦θ≦2π)の長さは、曲線y=x²/2(0≦θ≦2π)の長さに等しいことを示せ。
【数Ⅲ】【積分とその応用】次の曲線の長さLを求めよ。ただし、θは媒介変数a,p,qは定数であり、a>0,0<q<π/2 を満たす。

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の曲線の長さLを求めよ。ただし、θは媒介変数a,p,qは定数であり、a>0,0<q<π/2 を満たす。
(1) x=a(cosθ+θsinθ)、y=a(sinθ-θcosθ) (0≦θ≦p)
(2) y=log(cosx) (0≦θ≦p)
この動画を見る
次の曲線の長さLを求めよ。ただし、θは媒介変数a,p,qは定数であり、a>0,0<q<π/2 を満たす。
(1) x=a(cosθ+θsinθ)、y=a(sinθ-θcosθ) (0≦θ≦p)
(2) y=log(cosx) (0≦θ≦p)
【中学受験理科】【季節の変化と太陽③】図1のA~Cは、春分の日および秋分の日、夏至の日、冬至の日のいずれかの日の、日本での太陽の動きを表しています。これについて、次の問に答えなさい。※季節の変化と太…

単元:
#理科(中学受験)#地学分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図1のA~Cは、春分の日および秋分の日、夏至の日、冬至の日のいずれかの日の、日本での太陽の動きを表しています。これについて、次の問に答えなさい。※季節の変化と太陽②~④においては、太陽が最も高い位置に来たときの高度を正中高度と表現している。
問1 図1のA・Bのとき、赤道での太陽の動きと向きを下にかきなさい
問2 図1のB・Cのとき、赤道での日影曲線と影が動く向きを下にかきなさい
問3 図1のA・B・Cのとき、南緯40度の地点での太陽の正中高度はそれぞれ何度になりますか。なお、地軸は交点面に垂直な方向に大して23.4度傾いているものとします。
※表や図は動画内に記載
この動画を見る
図1のA~Cは、春分の日および秋分の日、夏至の日、冬至の日のいずれかの日の、日本での太陽の動きを表しています。これについて、次の問に答えなさい。※季節の変化と太陽②~④においては、太陽が最も高い位置に来たときの高度を正中高度と表現している。
問1 図1のA・Bのとき、赤道での太陽の動きと向きを下にかきなさい
問2 図1のB・Cのとき、赤道での日影曲線と影が動く向きを下にかきなさい
問3 図1のA・B・Cのとき、南緯40度の地点での太陽の正中高度はそれぞれ何度になりますか。なお、地軸は交点面に垂直な方向に大して23.4度傾いているものとします。
※表や図は動画内に記載
【受験算数】動点移動と相似:点PはEF上をEからFまで秒速3㎝で進みます。点QはCB上をCからBまで秒速3㎝で進みます。2点P、Qが同時に出発するとき、3点D、P、Qが一直線上に並ぶのは、何秒後ですか
単元:
#算数(中学受験)#速さ#点の移動・時計算
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
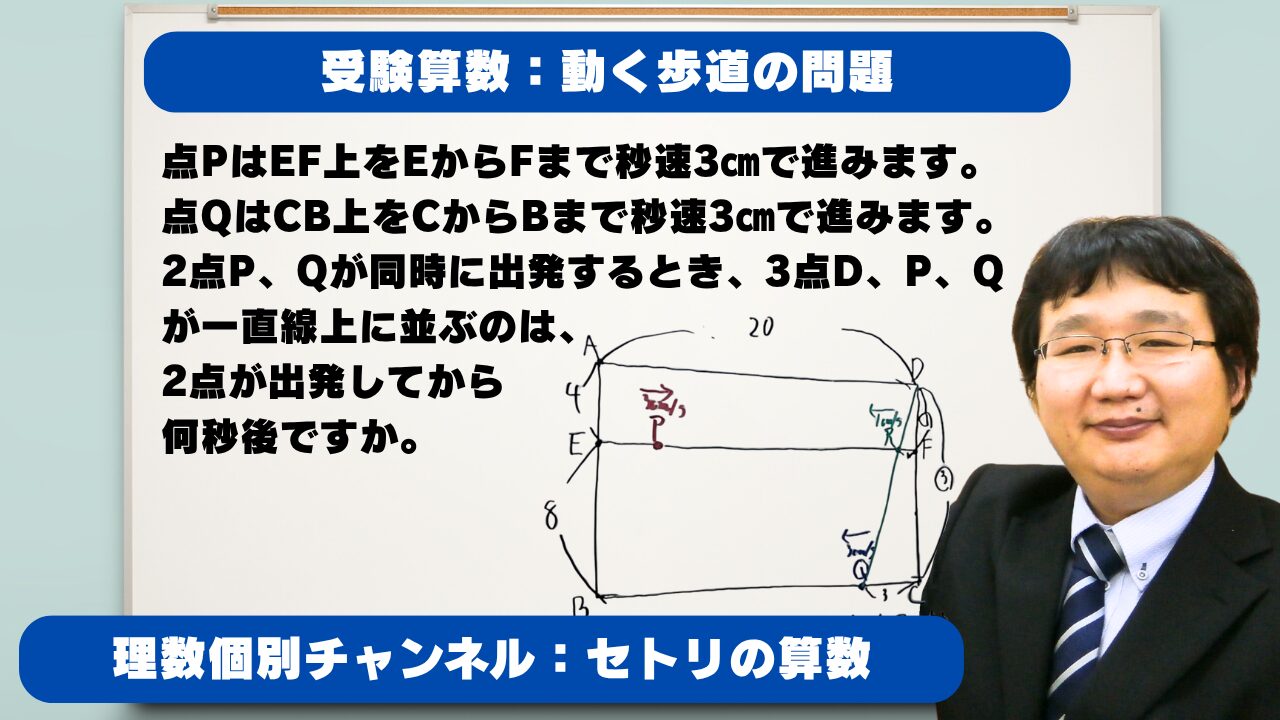
右の図は、長方形ABCDの中に直線EFを引いたもので、ADとEFは平行です。点PはEF上をEからFまで秒速3㎝で進みます。点QはCB上をCからBまで秒速3㎝で進みます。2点P、Qが同時に出発するとき、3点D、P、Qが一直線上に並ぶのは、2点が出発してから何秒後ですか。
この動画を見る
右の図は、長方形ABCDの中に直線EFを引いたもので、ADとEFは平行です。点PはEF上をEからFまで秒速3㎝で進みます。点QはCB上をCからBまで秒速3㎝で進みます。2点P、Qが同時に出発するとき、3点D、P、Qが一直線上に並ぶのは、2点が出発してから何秒後ですか。
【高校化学】【サリチル酸】サリチル酸の反応に関わる経路図について,各問いに答えよ。(図は本編中)(1) A, B にあてはまる化合物の構造式と物質名を記せ。(2) a,bにあてはまる…

単元:
#化学#有機#有機化合物の特徴と構造#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
サリチル酸の反応に関わる経路図について,各問いに答えよ。
(図は本編中)
(1) A, B にあてはまる化合物の構造式と物質名を記せ。
(2) a,bにあてはまる操作として,正しいものを選べ。
(ア) 水溶液にして、二酸化炭素を通じる。 (イ) 塩酸を加える (ウ)高温・高圧で二酸化炭素と反応させる
(3)次の化合物のうち、下の記述にあてはまるものをすべて選べ
(ア) サリチル酸 (イ) 化合物A (ウ) 化合物B
① 炭酸水素ナトリウム水溶液に、気体を発生しながら溶ける
② 塩化鉄(Ⅲ) 水溶液によって呈色する。
この動画を見る
サリチル酸の反応に関わる経路図について,各問いに答えよ。
(図は本編中)
(1) A, B にあてはまる化合物の構造式と物質名を記せ。
(2) a,bにあてはまる操作として,正しいものを選べ。
(ア) 水溶液にして、二酸化炭素を通じる。 (イ) 塩酸を加える (ウ)高温・高圧で二酸化炭素と反応させる
(3)次の化合物のうち、下の記述にあてはまるものをすべて選べ
(ア) サリチル酸 (イ) 化合物A (ウ) 化合物B
① 炭酸水素ナトリウム水溶液に、気体を発生しながら溶ける
② 塩化鉄(Ⅲ) 水溶液によって呈色する。
【数Ⅲ】【積分とその応用】半径がaである円Oの直径ABの両端AおよびBから出発して円Oの周上を同じ向きに動く2点P,QがPの速さはQの速さの2倍でAからBまで動くとき、△APQの面積の最大値を求めよ。

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
半径がaである円Oの直径ABの両端AおよびBから出発して円Oの周上を同じ向きにそれぞれ一定の速さで動く2点P,Qがある。Pの速さはQの速さの2倍で、PがAからBまで動くとき、△APQの面積の最大値を求めよ。また,その時の∠BOQの大きさを求めよ。
この動画を見る
半径がaである円Oの直径ABの両端AおよびBから出発して円Oの周上を同じ向きにそれぞれ一定の速さで動く2点P,Qがある。Pの速さはQの速さの2倍で、PがAからBまで動くとき、△APQの面積の最大値を求めよ。また,その時の∠BOQの大きさを求めよ。
【数Ⅲ】【積分とその応用】点Pが原点Oを中心とする半径rの円の周上を等速円運動OPが毎秒π/6ラジアンだけ回転するとき,点Pの速さと加速度の大きさを求めよ。

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
点Pが,原点Oを中心とする半径rの円の周上を,等速円運動。OPが毎秒π/6ラジアンだけ回転するとき,点Pの速さと加速度の大きさを求めよ。ただし,Pは円周上の点(r,0)から出発するものとする。
この動画を見る
点Pが,原点Oを中心とする半径rの円の周上を,等速円運動。OPが毎秒π/6ラジアンだけ回転するとき,点Pの速さと加速度の大きさを求めよ。ただし,Pは円周上の点(r,0)から出発するものとする。
【数Ⅲ】【積分とその応用】半径が10cm深さが20cmの直円錐形容器に毎秒3cm³の割合で静かに水を注ぐとき水の深さが6cmになった瞬間の水面の上昇する速さと水面の面積の増加する速さを求めよ。

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
上面の半径が10cm,深さが20cmの直円錐形の容器が,その軸を鉛直にして固定されている。この容器に毎秒3cm³の割合で静かに水を注ぐとき,水の深さが6cmになった瞬間の,水面の上昇する速さと,水面の面積の増加する速さを求めよ。
この動画を見る
上面の半径が10cm,深さが20cmの直円錐形の容器が,その軸を鉛直にして固定されている。この容器に毎秒3cm³の割合で静かに水を注ぐとき,水の深さが6cmになった瞬間の,水面の上昇する速さと,水面の面積の増加する速さを求めよ。
【中学受験理科】【季節の変化と太陽②】図1のA~Cは、春分の日および秋分の日、夏至の日、冬至の日のいずれかの日の、日本での太陽の動きを表しています。これについて、次の問に答えなさい。

単元:
#理科(中学受験)#地学分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図1のA~Cは、春分の日および秋分の日、夏至の日、冬至の日のいずれかの日の、日本での太陽の動きを表しています。これについて、次の問に答えなさい。※季節の変化と太陽②~④においては、太陽が最も高い位置に来たときの高度を正中高度と表現している。
問1 図1のAのとき、オーストラリアでの太陽の動きと向きを正しく表しているものを、図2のア~シから1つ選び、記号で答えなさい
問2 図1のCのとき、オーストラリアでの日影曲線と影が動く向きを正しく表しているものを、図3のア~シから1つ選び、記号で答えなさい
問3 図1のA・B・Cのとき、南緯40度の地点での太陽の正中高度はそれぞれ何度になりますか。なお、地軸は交点面に垂直な方向に大して23.4度傾いているものとします。
※表や図は動画内に記載
この動画を見る
図1のA~Cは、春分の日および秋分の日、夏至の日、冬至の日のいずれかの日の、日本での太陽の動きを表しています。これについて、次の問に答えなさい。※季節の変化と太陽②~④においては、太陽が最も高い位置に来たときの高度を正中高度と表現している。
問1 図1のAのとき、オーストラリアでの太陽の動きと向きを正しく表しているものを、図2のア~シから1つ選び、記号で答えなさい
問2 図1のCのとき、オーストラリアでの日影曲線と影が動く向きを正しく表しているものを、図3のア~シから1つ選び、記号で答えなさい
問3 図1のA・B・Cのとき、南緯40度の地点での太陽の正中高度はそれぞれ何度になりますか。なお、地軸は交点面に垂直な方向に大して23.4度傾いているものとします。
※表や図は動画内に記載
【垂直抗力の大きさ】図のように、重さ9.0Nの物体Aと3.0 Nの物体Bが静止している。(1)~(4)のそれぞれにおいて、物体Aが水平面から受ける垂直抗力の大きさをNとする。Nをそれぞれ求めよ。…

単元:
#物理#力学#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、重さ9.0Nの物体Aと3.0 Nの物体Bが静止している。(1)~(4)のそれぞれにおいて、物体Aが水平面から受ける垂直抗力の大きさをNとする。Nをそれぞれ求めよ。
この動画を見る
図のように、重さ9.0Nの物体Aと3.0 Nの物体Bが静止している。(1)~(4)のそれぞれにおいて、物体Aが水平面から受ける垂直抗力の大きさをNとする。Nをそれぞれ求めよ。
【受験算数】速さ:周期の利用 点Pと点Qが出会うのは、出発してから何秒後?

単元:
#算数(中学受験)#速さ#点の移動・時計算
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
大問1
120cmはなれた2点A、Bがあります。点PはAから、点QはBから同時に出発して、 PはBに、QはAに向かうものとします。このとき、点Pは3秒間動いて1秒間休み、 また3秒間動いて1秒間休むというように、これをくり返しながら進み、動いているときの速さは毎秒4cmです。点Qは5秒間動いて3秒間休み、これをくり返しながら進み、動いているときの速さは毎秒6cmです。このとき、次の問いに答えなさい。
(1) 点Pと点Qが出会うのは、出発してから何秒後ですか。
(2) 出会った点はAから何cmのところですか。
大問2
270cmはなれた2点A、Bがあります。点PはAから、点QはBから同時に出発して、 PはBに、QはAに向かうものとします。このとき、点Pは3秒間動いて1秒間休み、 また3秒間動いて1秒間休むというように、これをくり返しながら進み、動いているときの速さは毎秒4cmです。点Qは5秒間動いて1秒間休み、これをくり返しながら進み、動いているときの速さは毎秒8cmです。このとき、次の問いに答えなさい。
(1) 点Pと点Qが出会うのは、出発してから何秒後ですか。
(2) 出会った点はAから何cmのところですか。
この動画を見る
大問1
120cmはなれた2点A、Bがあります。点PはAから、点QはBから同時に出発して、 PはBに、QはAに向かうものとします。このとき、点Pは3秒間動いて1秒間休み、 また3秒間動いて1秒間休むというように、これをくり返しながら進み、動いているときの速さは毎秒4cmです。点Qは5秒間動いて3秒間休み、これをくり返しながら進み、動いているときの速さは毎秒6cmです。このとき、次の問いに答えなさい。
(1) 点Pと点Qが出会うのは、出発してから何秒後ですか。
(2) 出会った点はAから何cmのところですか。
大問2
270cmはなれた2点A、Bがあります。点PはAから、点QはBから同時に出発して、 PはBに、QはAに向かうものとします。このとき、点Pは3秒間動いて1秒間休み、 また3秒間動いて1秒間休むというように、これをくり返しながら進み、動いているときの速さは毎秒4cmです。点Qは5秒間動いて1秒間休み、これをくり返しながら進み、動いているときの速さは毎秒8cmです。このとき、次の問いに答えなさい。
(1) 点Pと点Qが出会うのは、出発してから何秒後ですか。
(2) 出会った点はAから何cmのところですか。




