 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【英語】2025神奈川県入試 追検査 英語 大問2から5をYAKISOBA先生が解説!

単元:
#英語(中学生)#高校入試過去問(英語)#神奈川県立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
神奈川県公立高等学校入学者選抜検査問題(令和7年度)の追試験の解説。文法問題編です。
この動画を見る
神奈川県公立高等学校入学者選抜検査問題(令和7年度)の追試験の解説。文法問題編です。
【数C】【平面上の曲線】中心の極座標が(a,0)で極Oを通る円をCとし、極Oを除くC上の動点をPとする。線分OPを1辺とする正方形OPQRを作るとき、点Qの軌跡の極方程式を求めよ。

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
aを正の定数とする。中心の極座標が(a,0)で極Oを通る円をCとし、極Oを除くC上の動点をPとする。線分OPを1辺とする正方形OPQRを作るとき、点Qの軌跡の極方程式を求めよ。
この動画を見る
aを正の定数とする。中心の極座標が(a,0)で極Oを通る円をCとし、極Oを除くC上の動点をPとする。線分OPを1辺とする正方形OPQRを作るとき、点Qの軌跡の極方程式を求めよ。
【数C】【平面上の曲線】極座標が(2,0)である点Aを通り始線OXに垂直な直線をlとし、極Oを端点とする半直線OP上に、OP・OQ=4を満たす点Qをとるとき、点Qの軌跡の極方程式を求めよ。

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
極座標が(2,0)である点Aを通り始線OXに垂直な直線をlとし、l上の動点をPとする。極Oを端点とする半直線OP上に、OP・OQ=4を満たす点Qをとるとき、点Qの軌跡の極方程式を求めよ。
この動画を見る
極座標が(2,0)である点Aを通り始線OXに垂直な直線をlとし、l上の動点をPとする。極Oを端点とする半直線OP上に、OP・OQ=4を満たす点Qをとるとき、点Qの軌跡の極方程式を求めよ。
【受験算数】割合:あるレストランの3種類の定食の値段

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
指導講師:
理数個別チャンネル
問題文全文(内容文):
大問1
あるレストランにはA、B、Cの3種類の定食があり、昨年の値段はAが一番安く、B、Cの順に200円ずつ高かったのですが、今年はA、B、Cの値段をそれぞれ3割、2割、1割上げたので、3種類の定食の値段の合計では、今年は昨年の【1と(11/60)】倍になりました。昨年のAの値段はいくらですか。
大問2
あるレストランにはA、B、Cの3種類の定食があり、昨年の値段はAが一番安く、B、Cの順に100円ずつ高かったのですが、今年はA、B、Cの値段をそれぞれ2割、3割、4割上げたので、3種類の定食の値段の合計では、今年は昨年の【1と(14/45)】倍になりました。今年のBの値段はいくらですか。
この動画を見る
大問1
あるレストランにはA、B、Cの3種類の定食があり、昨年の値段はAが一番安く、B、Cの順に200円ずつ高かったのですが、今年はA、B、Cの値段をそれぞれ3割、2割、1割上げたので、3種類の定食の値段の合計では、今年は昨年の【1と(11/60)】倍になりました。昨年のAの値段はいくらですか。
大問2
あるレストランにはA、B、Cの3種類の定食があり、昨年の値段はAが一番安く、B、Cの順に100円ずつ高かったのですが、今年はA、B、Cの値段をそれぞれ2割、3割、4割上げたので、3種類の定食の値段の合計では、今年は昨年の【1と(14/45)】倍になりました。今年のBの値段はいくらですか。
【振り子のエネルギー】長さ0.40mの糸の先におもりをつけ、点Oからつるして振り子をつくった。糸がたるまないように、鉛直方向とのなす角が60°となる位置まで引き上げ、おもりを静かにはなす。点Oの真下…

単元:
#物理#力学#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
長さ0.40mの糸の先におもりをつけ、点Oからつるして振り子をつくった。糸がたるまないように、鉛直方向とのなす角が60°となる位置まで引き上げ、おもりを静かにはなす。点Oの真下で0から0.20mの位置に釘がある。重力加速度の大きさを9.8とする。
(1) おもりが最下点に達したときの速さはいくらか。
(2)最下点を過ぎると糸が釘に引っかかり、釘を支点として振り子が振れる。鈴直方向と糸とのなす角が60°となるとき、おもりの速さはいくらか。
(3)おもりが最高点に達したとき、糸と鉛直方向とのなす角はいくらか。
この動画を見る
長さ0.40mの糸の先におもりをつけ、点Oからつるして振り子をつくった。糸がたるまないように、鉛直方向とのなす角が60°となる位置まで引き上げ、おもりを静かにはなす。点Oの真下で0から0.20mの位置に釘がある。重力加速度の大きさを9.8とする。
(1) おもりが最下点に達したときの速さはいくらか。
(2)最下点を過ぎると糸が釘に引っかかり、釘を支点として振り子が振れる。鈴直方向と糸とのなす角が60°となるとき、おもりの速さはいくらか。
(3)おもりが最高点に達したとき、糸と鉛直方向とのなす角はいくらか。
【受験算数】普通の道を歩く速さは、母は分速85m、子は分速65mです。母と子が「動く歩道」の上を歩いてA地点からB地点まで行くのに、母は8分、子は10分かかります。「動く歩道」の速さは分速何mですか。

単元:
#算数(中学受験)#速さ#速さその他
教材:
#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
A地点からB地点に向かう「動く歩道」があります。普通の道を歩く時の速さは、母は分速85m、子は分速65mです。母と子が「動く歩道」の上を歩いてA地点からB地点まで行くのに、母は8分、子は10分かかります。「動く歩道」の速さは分速何mですか。また、A地点からB地点までの距離は何mですか。
この動画を見る
A地点からB地点に向かう「動く歩道」があります。普通の道を歩く時の速さは、母は分速85m、子は分速65mです。母と子が「動く歩道」の上を歩いてA地点からB地点まで行くのに、母は8分、子は10分かかります。「動く歩道」の速さは分速何mですか。また、A地点からB地点までの距離は何mですか。
【数C】【ベクトルの内積】ベクトルa=(1,1),b=(1,-1),c=(1,2)に対して,(xa+yb)⊥c,|xa+yb|=2√5であるように,実数x,yの値を求めよ。

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
ベクトル $\vec{a}=(1,1), \vec{b} = (1,-1), \vec{c} = (1,2)$ に対して、
$(x \vec{a} + y \vec{b}) \perp \vec{c}, |x \vec{a}+ y \vec{b}| = 2 \sqrt{5}$ であるように、
実数$x,y$ の値を定めよ。
この動画を見る
ベクトル $\vec{a}=(1,1), \vec{b} = (1,-1), \vec{c} = (1,2)$ に対して、
$(x \vec{a} + y \vec{b}) \perp \vec{c}, |x \vec{a}+ y \vec{b}| = 2 \sqrt{5}$ であるように、
実数$x,y$ の値を定めよ。
【音の計算2】空気中を伝わる音の速さを毎秒340mとして、次の問いに答えなさい。問1 毎秒10mの速さで、岩べきに向かって進む船が笛を鳴らしたところ、3秒後に反射音を聞きました。反射音を聞いたときの…

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
空気中を伝わる音の速さを毎秒340mとして、次の問いに答えなさい。
問1 毎秒10mの速さで、岩べきに向かって進む船が笛を鳴らしたところ、3秒後に反射音を聞きました。反射音を聞いたときの船の位置は、岩べきから何mのところですか。
問2 問1のとき7秒間汽笛を鳴らしたとすると、岩べきからの反射音は何秒間聞こえましたか。
問3 問2のとき1秒間に3回の割合で汽笛を鳴らしたとすると、反射会は1秒間に何回の割合で関こえましたか。小数第2位を四捨五入して答えなさい。
この動画を見る
空気中を伝わる音の速さを毎秒340mとして、次の問いに答えなさい。
問1 毎秒10mの速さで、岩べきに向かって進む船が笛を鳴らしたところ、3秒後に反射音を聞きました。反射音を聞いたときの船の位置は、岩べきから何mのところですか。
問2 問1のとき7秒間汽笛を鳴らしたとすると、岩べきからの反射音は何秒間聞こえましたか。
問3 問2のとき1秒間に3回の割合で汽笛を鳴らしたとすると、反射会は1秒間に何回の割合で関こえましたか。小数第2位を四捨五入して答えなさい。
【数C】【平面上の曲線】eは正の定数とする。極座標が(3,0)である点Aを通り、OXに垂直な直線をlとする。極Oと直線lからの比がe:1である点Pの極方程式を求めよ。(1)e=1(2)e=1/2

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
eは正の定数とする。極座標が(3,0)である点Aを通り、始線OXに垂直な直線をlとする。極Oと直線lからの距離の比がe:1である点Pの軌跡を表す極方程式を、次の各場合について求めよ。
(1)e=1
(2)e=1/2
この動画を見る
eは正の定数とする。極座標が(3,0)である点Aを通り、始線OXに垂直な直線をlとする。極Oと直線lからの距離の比がe:1である点Pの軌跡を表す極方程式を、次の各場合について求めよ。
(1)e=1
(2)e=1/2
【数C】【平面上の曲線】次の極方程式はどのような曲線を表すか。直交座標の方程式に直して答えよ。(1)r=1/√2+cosθ(2)r=3/1+2cosθ(3)r=2/1+cosθ

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の極方程式はどのような曲線を表すか。
直交座標の方程式に直して答えよ。
(1)$r=\dfrac{1}{\sqrt{2}+cosθ}$
(2)$r=\dfrac{3}{1+2cosθ}$
(3)$r=\dfrac{2}{1+cosθ}$
この動画を見る
次の極方程式はどのような曲線を表すか。
直交座標の方程式に直して答えよ。
(1)$r=\dfrac{1}{\sqrt{2}+cosθ}$
(2)$r=\dfrac{3}{1+2cosθ}$
(3)$r=\dfrac{2}{1+cosθ}$
滑車につるした物体の運動 図のように、なめらかにまわる軽い滑車に軽い糸を通し、糸の両端に質量3.0kgの物体Aと質量4.0kgの物体Bをつけて、手で支えている。その後、静かに手をはなした。重力加速度…

単元:
#物理#力学#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、なめらかにまわる軽い滑車に軽い糸を通し、糸の両端に質量3.0kgの物体Aと質量4.0kgの物体Bをつけて、手で支えている。その後、静かに手をはなした。重力加速度の大きさを9.8とし、糸は十分に長いものとして、次の各問に答えよ。
この動画を見る
図のように、なめらかにまわる軽い滑車に軽い糸を通し、糸の両端に質量3.0kgの物体Aと質量4.0kgの物体Bをつけて、手で支えている。その後、静かに手をはなした。重力加速度の大きさを9.8とし、糸は十分に長いものとして、次の各問に答えよ。
【受験算数】5/24=1/A+1/Bが成り立つとき、2つの整数A、Bの組として考えられるものを(A,B)の形ですべて答えなさい。ただし、A<Bとします。

単元:
#算数(中学受験)#計算と数の性質#数の性質その他
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\displaystyle\frac{5}{24}=\frac{1}{A}+\frac{1}{B}$が成り立つとき、2つの整数A、Bの組として考えられるものを(A,B)の形ですべて答えなさい。ただし、A<Bとします。
この動画を見る
$\displaystyle\frac{5}{24}=\frac{1}{A}+\frac{1}{B}$が成り立つとき、2つの整数A、Bの組として考えられるものを(A,B)の形ですべて答えなさい。ただし、A<Bとします。
【数C】【平面上の曲線】4点A(a,0)B(0,b)C(-a,0)D(0,-8)(a>0,b>0)を頂点とするひし形ABCDがある。PA・PC=PB・PDを満たす点Pの軌跡を求めよ。

単元:
#平面上の曲線#2次曲線#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
$4$ 点 $\mathrm{ A }(a, \ 0),\ \mathrm{ B }(0, \ b),\ \mathrm{ C }(-a, \ 0),\ \mathrm{ D }(0, \ -b) \ (a \gt 0, \ b \gt 0)$
を頂点とするひし形 $\mathrm{ABCD}$ がある。
$\mathrm{PA \cdot PC } = \mathrm{PB \cdot PD}$ を満たす点$\mathrm{P}$ の軌跡を求めよ。
この動画を見る
$4$ 点 $\mathrm{ A }(a, \ 0),\ \mathrm{ B }(0, \ b),\ \mathrm{ C }(-a, \ 0),\ \mathrm{ D }(0, \ -b) \ (a \gt 0, \ b \gt 0)$
を頂点とするひし形 $\mathrm{ABCD}$ がある。
$\mathrm{PA \cdot PC } = \mathrm{PB \cdot PD}$ を満たす点$\mathrm{P}$ の軌跡を求めよ。
【数C】【平面上の曲線】直角双曲線x²-y²=a² (a>0)上の点Pから、2つの漸近線に垂線PQ,PRを下ろす。このとき、PQ・PRは一定であることを証明せよ

単元:
#平面上の曲線#2次曲線#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
直角双曲線 $x^2+y^2=a^2 \ (a \gt 0)$ 上の点$\mathrm{P}$ から、
$2$ つの漸近線に垂線$\mathrm{PQ,PR}$ を下ろす。
このとき、 $\mathrm{PQ \cdot PR}$ は一定であることを証明せよ。
この動画を見る
直角双曲線 $x^2+y^2=a^2 \ (a \gt 0)$ 上の点$\mathrm{P}$ から、
$2$ つの漸近線に垂線$\mathrm{PQ,PR}$ を下ろす。
このとき、 $\mathrm{PQ \cdot PR}$ は一定であることを証明せよ。
【音の計算1】気温が15℃のとき、次の問いに答えなさい。1 音の速さは秒速何mですか。間2 1.7km離れた場所で雪が落ちました。音が聞こえるのは何秒後ですか。間3 612m離れた壁に向かって音を出…

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard
指導講師:
理数個別チャンネル
問題文全文(内容文):
気温が15℃のとき、次の問いに答えなさい。
問1 音の速さは秒速何mですか。
間2 1.7km離れた場所で雪が落ちました。音が聞こえるのは何秒後ですか。
間3 612m離れた壁に向かって音を出すと、反射した音が聞こえるのは何秒後ですか。
問4 秒速15mで壁に向かって動いている車が、壁から2130mのところでサイレンを鳴らしました。車にいる人は何秒後に反射音を聞きましたか。
問5 時速36kmで壁から遠ざかりながら動いている車がサイレンを鳴らすと、6秒後に反射音が聞こえました。反射音を聞いたときの壁までの距離は何mですか。
この動画を見る
気温が15℃のとき、次の問いに答えなさい。
問1 音の速さは秒速何mですか。
間2 1.7km離れた場所で雪が落ちました。音が聞こえるのは何秒後ですか。
間3 612m離れた壁に向かって音を出すと、反射した音が聞こえるのは何秒後ですか。
問4 秒速15mで壁に向かって動いている車が、壁から2130mのところでサイレンを鳴らしました。車にいる人は何秒後に反射音を聞きましたか。
問5 時速36kmで壁から遠ざかりながら動いている車がサイレンを鳴らすと、6秒後に反射音が聞こえました。反射音を聞いたときの壁までの距離は何mですか。
【光電効果】金属に、光をあてた。(1)この光の光子1個のエネルギーは?(2)金属から飛び出す光電子の運動エネルギーの最大値は?(3)光の強さだけを1/2倍にした。光電子の運動エネルギーの最大値は?

単元:
#物理#理科(高校生)#原子
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
仕事関数3.8✕10^-19Jの金属に、波長3.3✕10^-3mの光をあてた。真空中の光速を3.0x10^8m/s,プランク定数を6.6✕10^-34J・Sとして、次の各問に答えよ。
(1)この光の光子1個のエネルギーはいくらか。
(2)金属から飛び出す光電子の運動エネルギーの最大値はいくらか。
(3)光の強さだけを1/2倍にした。光電子の運動エネルギーの最大値はいくらになるか。
この動画を見る
仕事関数3.8✕10^-19Jの金属に、波長3.3✕10^-3mの光をあてた。真空中の光速を3.0x10^8m/s,プランク定数を6.6✕10^-34J・Sとして、次の各問に答えよ。
(1)この光の光子1個のエネルギーはいくらか。
(2)金属から飛び出す光電子の運動エネルギーの最大値はいくらか。
(3)光の強さだけを1/2倍にした。光電子の運動エネルギーの最大値はいくらになるか。
【受験算数】割合:ボールのはね上がりの処理
単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
大問1
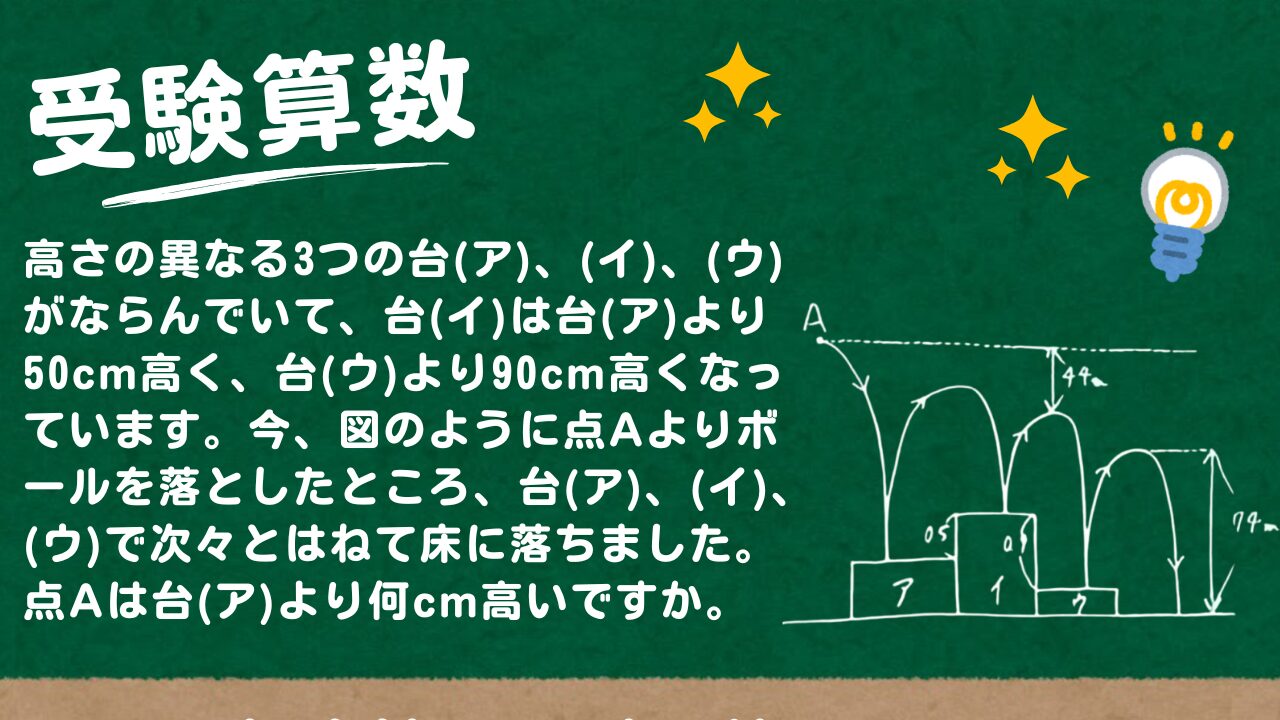
高さの異なる3つの台(ア)、(イ)、(ウ)がならんでいて、台(イ)は台(ア)より50cm高く、台(ウ)より90cm高くなっています。今、図のように点Aよりボールを落としたところ、台(ア)、(イ)、(ウ)で次々とはねて床に落ちました。台(イ)ではねたあと、もっとも高くなった時の高さは、Aの高さより4.4m低く、台(ウ) ではねたあと、もっとも高くなった時の高さは、床か ら7.4mでした。ただし、このボールは落ちた高さの80%だけはねあがることとします。
(1)点Aは台(ア)より何cm高いですか。
(2)台(ア)の高さは何cmですか。
大問2
高さの異なる3つの台(ア)、(イ)、(ウ)がならんでいて、台(イ)は台(ア)より40cm高く、台(ウ)より90cm高くなっています。今、図のように点Aよりボールを落としたところ、台(ア)、(イ)、(ウ)で次々とはねて床に落ちました。台(イ)ではねたあと、もっとも高くなった時の高さは、Aの高さより1.3m低く、台(ウ) ではねたあと、もっとも高くなった時の高さは、床か ら2.3mでした。ただし、このボールは落ちた高さの75%だけはねあがることとします。
(1)点Aは台(ア)より何cm高いですか。
(2)台(ア)の高さは何cmですか。
この動画を見る
大問1
高さの異なる3つの台(ア)、(イ)、(ウ)がならんでいて、台(イ)は台(ア)より50cm高く、台(ウ)より90cm高くなっています。今、図のように点Aよりボールを落としたところ、台(ア)、(イ)、(ウ)で次々とはねて床に落ちました。台(イ)ではねたあと、もっとも高くなった時の高さは、Aの高さより4.4m低く、台(ウ) ではねたあと、もっとも高くなった時の高さは、床か ら7.4mでした。ただし、このボールは落ちた高さの80%だけはねあがることとします。
(1)点Aは台(ア)より何cm高いですか。
(2)台(ア)の高さは何cmですか。
大問2
高さの異なる3つの台(ア)、(イ)、(ウ)がならんでいて、台(イ)は台(ア)より40cm高く、台(ウ)より90cm高くなっています。今、図のように点Aよりボールを落としたところ、台(ア)、(イ)、(ウ)で次々とはねて床に落ちました。台(イ)ではねたあと、もっとも高くなった時の高さは、Aの高さより1.3m低く、台(ウ) ではねたあと、もっとも高くなった時の高さは、床か ら2.3mでした。ただし、このボールは落ちた高さの75%だけはねあがることとします。
(1)点Aは台(ア)より何cm高いですか。
(2)台(ア)の高さは何cmですか。
【油脂の構成】構成脂肪酸がパルミチン酸C₁₅H₃₁COOH (分子量256)およびリノール酸C₁₇H₃₁COOH (分子量280) のみである油脂がある。 この油脂における構成脂肪酸の比は、パルミチ…

単元:
#化学#有機#有機化合物の特徴と構造#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
構成脂肪酸がパルミチン酸C₁₅H₃₁COOH (分子量256)および
リノール酸C₁₇H₃₁COOH (分子量280) のみである油脂がある。
この油脂における構成脂肪酸の比は、パルミチン酸1.0molに対して
リノール酸1.5molである。 次の各問いに答えよ。
(1)この油脂の平均分子量を整数値で求めよ。
(2)この油脂 100gを水酸化ナトリウムを用いてけん化するとき,必要な水酸化ナトリ
ウムの質量は何gか。 (1) で求めた整数値を用いて計算せよ。
(3)この油脂 100gにヨウ素を付加させるとき,必要なヨウ素の質量は何gか。 (1) で
求めた整数値を用いて計算せよ。
(4) パルミチン酸1分子とリノール酸2分子を含む油脂の構造異性体は、 いくつ存在
するか。また,その中に不斉炭素原子をもつものは,いくつあるか。
この動画を見る
構成脂肪酸がパルミチン酸C₁₅H₃₁COOH (分子量256)および
リノール酸C₁₇H₃₁COOH (分子量280) のみである油脂がある。
この油脂における構成脂肪酸の比は、パルミチン酸1.0molに対して
リノール酸1.5molである。 次の各問いに答えよ。
(1)この油脂の平均分子量を整数値で求めよ。
(2)この油脂 100gを水酸化ナトリウムを用いてけん化するとき,必要な水酸化ナトリ
ウムの質量は何gか。 (1) で求めた整数値を用いて計算せよ。
(3)この油脂 100gにヨウ素を付加させるとき,必要なヨウ素の質量は何gか。 (1) で
求めた整数値を用いて計算せよ。
(4) パルミチン酸1分子とリノール酸2分子を含む油脂の構造異性体は、 いくつ存在
するか。また,その中に不斉炭素原子をもつものは,いくつあるか。
2025年5月実施共通テスト模試「情報Ⅰ」大問3解説!

単元:
#情報Ⅰ(高校生)#プログラミング#アルゴリズムの表し方とプログラムの設計#探索と整列のプログラム#プログラムによる動的シミュレーション
指導講師:
理数個別チャンネル
問題文全文(内容文):
2025年5月実施共通テスト模試「情報Ⅰ」大問3解説!
この動画を見る
2025年5月実施共通テスト模試「情報Ⅰ」大問3解説!
【数C】【平面上の曲線】楕円x²/8+y²/4=1上の点(2,√2) を通り、この楕円の焦点を焦点とする双曲線の方程式を求めよ。また、双曲線の漸近線の方程式も求めよ。

単元:
#平面上の曲線#2次曲線#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
楕円 $\displaystyle \frac{x^2}{8}+\frac{y^2}{4}=1$ 上の点 $(2,\ \sqrt{2})$を通り、
この楕円の焦点を焦点とする双曲線の方程式を求めよ。
また、双曲線の漸近線の方程式も求めよ。
この動画を見る
楕円 $\displaystyle \frac{x^2}{8}+\frac{y^2}{4}=1$ 上の点 $(2,\ \sqrt{2})$を通り、
この楕円の焦点を焦点とする双曲線の方程式を求めよ。
また、双曲線の漸近線の方程式も求めよ。
【数C】【平面上の曲線】x²/a²-y²/b²=1の焦点と漸近線の距離を求めよ

単元:
#平面上の曲線#2次曲線#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
双曲線 $\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=1$$\ (a \gt 0,\ b \gt 0)$
の焦点と漸近線の距離を求めよ。
この動画を見る
双曲線 $\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=1$$\ (a \gt 0,\ b \gt 0)$
の焦点と漸近線の距離を求めよ。
【数C】【ベクトルの内積】a・b= b・c=c・a=-2,a+b+c=0とする。(1) a , b , c の大きさを求めよ。(2) a と b のなす角θを求めよ

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{c} = \vec{c} \cdot \vec{a} = -2$ ,
$ \vec{a} + \vec{b} + \vec{c} = \vec{0}$とする。
(1) $\vec{a} , \vec{b} , \vec{c}$ の大きさを求めよ。
(2) $\vec{a}$ と $\vec{b}$ のなす角 $\theta$ を求めよ。
この動画を見る
$\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{c} = \vec{c} \cdot \vec{a} = -2$ ,
$ \vec{a} + \vec{b} + \vec{c} = \vec{0}$とする。
(1) $\vec{a} , \vec{b} , \vec{c}$ の大きさを求めよ。
(2) $\vec{a}$ と $\vec{b}$ のなす角 $\theta$ を求めよ。
【数C】【ベクトルの内積】0でない2つのベクトルa, bについて、|a+b|=|a-b|ならばa⊥bであることを示せ

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\vec{0}$でない2つのベクトル$\vec{a}, \vec{b}$について、
$|\vec{a}+\vec{b}|=|\vec{a}-\vec{b}|$ならば
$\vec{a} \perp \vec{b}$であることを示せ。
この動画を見る
$\vec{0}$でない2つのベクトル$\vec{a}, \vec{b}$について、
$|\vec{a}+\vec{b}|=|\vec{a}-\vec{b}|$ならば
$\vec{a} \perp \vec{b}$であることを示せ。
【数C】【ベクトルの内積】ベクトルa=(-1,7)と45°の角をなし, 大きさが5であるベクトルxを求めよ

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
ベクトル$\vec{a}=(-1,7)$と
45°の角をなし,
大きさが5である
ベクトル$\vec{x}$を求めよ。
この動画を見る
ベクトル$\vec{a}=(-1,7)$と
45°の角をなし,
大きさが5である
ベクトル$\vec{x}$を求めよ。
【数C】【ベクトルの内積】2つのベクトルx, yが2x-y=(0,4), 2|x|=|y|, xy=6を満たすとき, x, yを求めよ。

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
2つのベクトル$\vec{x}, \vec{y}$が$2\vec{x}-\vec{y}=(0,4)$,
$2|\vec{x}|=|\vec{y}|, \vec{x}\cdot\vec{y}=6$を満たすとき,
$\vec{x}, \vec{y}$を求めよ。
この動画を見る
2つのベクトル$\vec{x}, \vec{y}$が$2\vec{x}-\vec{y}=(0,4)$,
$2|\vec{x}|=|\vec{y}|, \vec{x}\cdot\vec{y}=6$を満たすとき,
$\vec{x}, \vec{y}$を求めよ。
【数C】【ベクトルの内積】|a|=3,|b|=4,|a-b|=3のとき,|a+tb|を最小にする実数tの値とその最小値を求めよ。

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
ベクトル$|\vec{a}|=3$、$|\vec{b}|=4$、$|\vec{a}-\vec{b}|=3$のとき、
$|\vec{a}+t\vec{b}|$を最小にする実数tの値とその最小値を求めよ。
この動画を見る
ベクトル$|\vec{a}|=3$、$|\vec{b}|=4$、$|\vec{a}-\vec{b}|=3$のとき、
$|\vec{a}+t\vec{b}|$を最小にする実数tの値とその最小値を求めよ。
【受験算数】15×15×15×15×15×15×15×15(15を8個かけあわせた数)を12で割って商を整数で求めるとき、あまりはいくつになりますか。

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
割り算のあまりについて、次の問いに答えなさい。
(1)4けたの整数「8□74」を9で割ると6あまるとき、□にあてはまる数字はいくつですか。
(2)6けたの整数「2891□5」を8でWると3あまるとき、□にあてはまる数字をすべて答えなさい。
(3)15×15×15×15×15×15×15×15(15を8個かけあわせた数)を12で割って商を整数で求めるとき、あまりはいくつになりますか。
この動画を見る
割り算のあまりについて、次の問いに答えなさい。
(1)4けたの整数「8□74」を9で割ると6あまるとき、□にあてはまる数字はいくつですか。
(2)6けたの整数「2891□5」を8でWると3あまるとき、□にあてはまる数字をすべて答えなさい。
(3)15×15×15×15×15×15×15×15(15を8個かけあわせた数)を12で割って商を整数で求めるとき、あまりはいくつになりますか。
【数C】【平面上の曲線】x²/16+y²/25 =1とy軸の交点をA、Bとする。楕円上の点をPとし、直線PA, PBとx軸の交点をそれぞれQ, R とするとき、 OQ・ORの値は一定であることを示せ。

単元:
#平面上の曲線#2次曲線#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
原点を $\mathrm{O}$、楕円 $\displaystyle \frac{x^2}{16}+\frac{y^2}{25}=1$ と $y$ 軸の交点を $\mathrm{A,B}$ とする。
$\mathrm{A,B}$ 以外の楕円上の点を$\mathrm{P}$ とし、直線 $\mathrm{PA,\ PB}$ と $x$ 軸の交点をそれぞれ $\mathrm{Q,R}$ とするとき、
$\mathrm{OQ \cdot OR}$ の値は一定であることを示せ。
この動画を見る
原点を $\mathrm{O}$、楕円 $\displaystyle \frac{x^2}{16}+\frac{y^2}{25}=1$ と $y$ 軸の交点を $\mathrm{A,B}$ とする。
$\mathrm{A,B}$ 以外の楕円上の点を$\mathrm{P}$ とし、直線 $\mathrm{PA,\ PB}$ と $x$ 軸の交点をそれぞれ $\mathrm{Q,R}$ とするとき、
$\mathrm{OQ \cdot OR}$ の値は一定であることを示せ。
【数C】【平面上の曲線】2点 A(- 2, 0) , B(2, 0) と楕円 x²/36 + y²/9 = 1上の点Qでできる△AQBの重心Pの軌跡を求めよ。

単元:
#平面上の曲線#2次曲線#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
$2$ 点 $\mathrm{A}(-2,\ 0),\ \mathrm{B}(2,\ 0)$と、
楕円 $\displaystyle \frac{x^2}{36}+\frac{y^2}{9}=1$ 上の点$\mathrm{Q}$でできる
$\triangle \mathrm{AQB}$ の重心$\mathrm{P}$の軌跡を求めよ。
この動画を見る
$2$ 点 $\mathrm{A}(-2,\ 0),\ \mathrm{B}(2,\ 0)$と、
楕円 $\displaystyle \frac{x^2}{36}+\frac{y^2}{9}=1$ 上の点$\mathrm{Q}$でできる
$\triangle \mathrm{AQB}$ の重心$\mathrm{P}$の軌跡を求めよ。
【数C】【平面上の曲線】長さ8の線分ABの端点Aは軸上を、 端点Bはy軸上を動くとする。(1) 線分ABを5:3に内分する点Pの軌跡を求めよ。(2) 線分ABを5:3に外分する点Qの軌跡を求めよ。

単元:
#平面上の曲線#2次曲線#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
長さ $8$ の線分 $\mathrm{AB}$ の端点$\mathrm{A}$ は $x$ 軸上を、
端点$\mathrm{B}$ は $y$ 軸上を動くとする。
(1) 線分 $\mathrm{AB}$ を $5:3$ に内分する点 $\mathrm{P}$ の軌跡を求めよ。
(2) 線分 $\mathrm{AB}$ を $5:3$ に外分する点 $\mathrm{Q}$ の軌跡を求めよ。
この動画を見る
長さ $8$ の線分 $\mathrm{AB}$ の端点$\mathrm{A}$ は $x$ 軸上を、
端点$\mathrm{B}$ は $y$ 軸上を動くとする。
(1) 線分 $\mathrm{AB}$ を $5:3$ に内分する点 $\mathrm{P}$ の軌跡を求めよ。
(2) 線分 $\mathrm{AB}$ を $5:3$ に外分する点 $\mathrm{Q}$ の軌跡を求めよ。




