 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【受験算数】割合:出し入れ(2)1

単元:
#算数(中学受験)#文章題#売買損益と食塩水
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
15%の食塩水が100gあります。これから40gの食塩水を取り出して、そのかわりに水を50g入れ、こうしてできた食塩水から、今度は55gを取り出し、水を20g 入れると、何%の食塩水になりますか。
この動画を見る
15%の食塩水が100gあります。これから40gの食塩水を取り出して、そのかわりに水を50g入れ、こうしてできた食塩水から、今度は55gを取り出し、水を20g 入れると、何%の食塩水になりますか。
【2025年度過去問解説】北海道大学 化学 問題3【構造決定行脚】

【数Ⅲ】【積分とその応用】定積分の種々の問題6 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の等式を満たす関数$f(x)$を求めよ。
(1) $\displaystyle f(x)=x+\int_0^2f(t)e^t~dt$
(2) $\displaystyle f(x)=\sin x-\int_0^\frac\pi3\{f(t)-\frac\pi3\}\sin t~dt$
この動画を見る
次の等式を満たす関数$f(x)$を求めよ。
(1) $\displaystyle f(x)=x+\int_0^2f(t)e^t~dt$
(2) $\displaystyle f(x)=\sin x-\int_0^\frac\pi3\{f(t)-\frac\pi3\}\sin t~dt$
【数Ⅲ】【積分とその応用】定積分の種々の問題5 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数$f(x)$の最大値、最小値を求めよ。
(1) $\displaystyle f(x)=\int_0^x(1+2\cos t)\sin t~dt~~(0\leqq x\leqq2\pi)$
(2) $\displaystyle f(x)=\int_1^x(2-t)\log t~dt~~(1\leqq x\leqq e)$
この動画を見る
次の関数$f(x)$の最大値、最小値を求めよ。
(1) $\displaystyle f(x)=\int_0^x(1+2\cos t)\sin t~dt~~(0\leqq x\leqq2\pi)$
(2) $\displaystyle f(x)=\int_1^x(2-t)\log t~dt~~(1\leqq x\leqq e)$
【数Ⅲ】【積分とその応用】定積分の種々の問題4 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数$\displaystyle f(x)=\int_0^{x}\sin 2t~dt~~(0\leqq x\leqq 2\pi)$
の極値を求めよ。
この動画を見る
関数$\displaystyle f(x)=\int_0^{x}\sin 2t~dt~~(0\leqq x\leqq 2\pi)$
の極値を求めよ。
【受験算数】割合:出し入れ(1)2

単元:
#算数(中学受験)#文章題#売買損益と食塩水
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
水120gに食塩30gを溶かし、よく混ぜ合わせた食塩水100gがあります。この食塩水を25gくみ出して捨て、そのあと、水15gを加えてよく混ぜ合わせました。
そして、その食塩水を56g取り出しました。取り出した食塩水56gの中には、食塩が何g溶けていますか?
この動画を見る
水120gに食塩30gを溶かし、よく混ぜ合わせた食塩水100gがあります。この食塩水を25gくみ出して捨て、そのあと、水15gを加えてよく混ぜ合わせました。
そして、その食塩水を56g取り出しました。取り出した食塩水56gの中には、食塩が何g溶けていますか?
【2025年度過去問解説】東京科学大学 化学 問題Ⅲ【構造決定行脚】

【数Ⅲ】【積分とその応用】定積分の種々の問題3 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数$\displaystyle F(x)=\int_x^{2x^2}(x+t)\sin t~dt$
を$x$について微分せよ。
この動画を見る
関数$\displaystyle F(x)=\int_x^{2x^2}(x+t)\sin t~dt$
を$x$について微分せよ。
【数Ⅲ】【積分とその応用】定積分の種々の問題2 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数を$x$について微分せよ。
(1) $\displaystyle y=\int_x^{2x}\cos^2t~dt$
(2) $\displaystyle y=\int_x^{x^2}e^t\sin t~dt$
この動画を見る
次の関数を$x$について微分せよ。
(1) $\displaystyle y=\int_x^{2x}\cos^2t~dt$
(2) $\displaystyle y=\int_x^{x^2}e^t\sin t~dt$
【数Ⅲ】【積分とその応用】定積分の種々の問題1 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数を$x$について微分せよ。
(1) $\displaystyle F(x)=\int_0^x(x+t)e^t~dt$
(2) $\displaystyle F(x)=\int_1^x(t-x)\log t~dt$
この動画を見る
次の関数を$x$について微分せよ。
(1) $\displaystyle F(x)=\int_0^x(x+t)e^t~dt$
(2) $\displaystyle F(x)=\int_1^x(t-x)\log t~dt$
【数C】【複素数平面】複素数と図形12 ※問題文は概要欄
単元:
#複素数平面#図形への応用#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
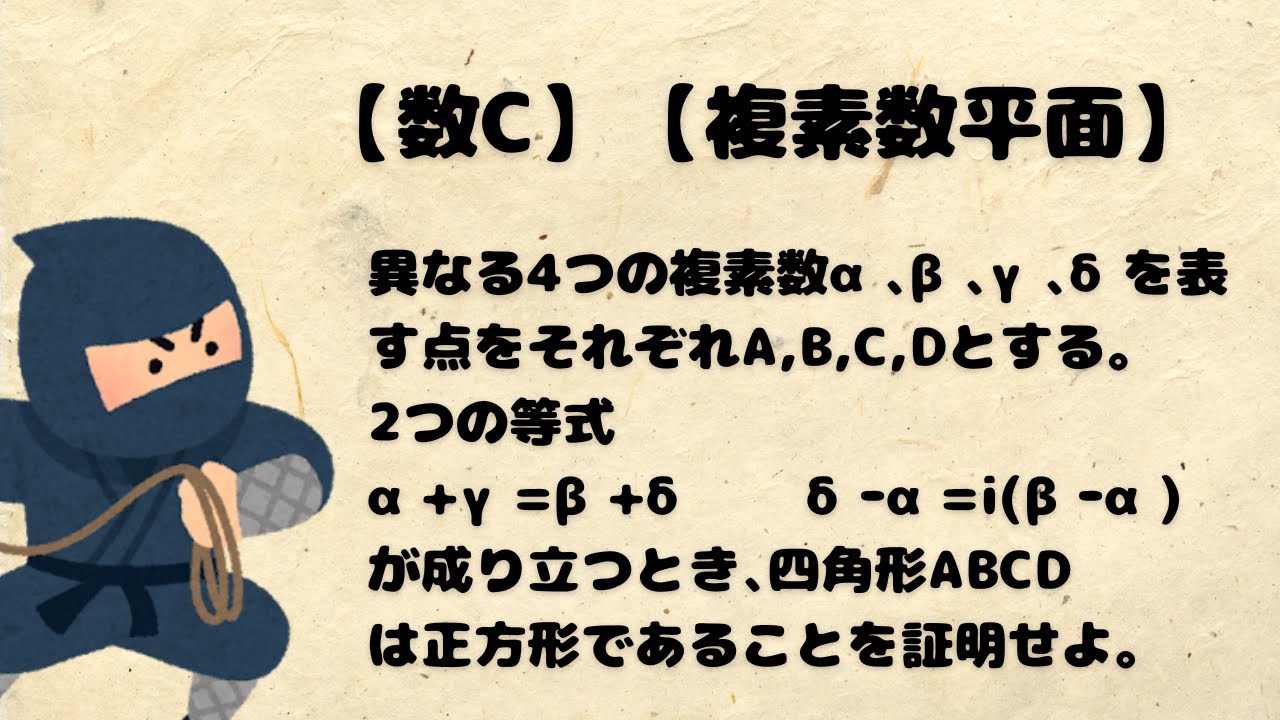
異なる4つの複素数α、β、γ、δを表す点を
それぞれA,B,C,Dとする。2つの等式
α+γ=β+δ δーα=i(βーα)
が成り立つとき、四角形ABCD
は正方形であることを証明せよ。
この動画を見る
異なる4つの複素数α、β、γ、δを表す点を
それぞれA,B,C,Dとする。2つの等式
α+γ=β+δ δーα=i(βーα)
が成り立つとき、四角形ABCD
は正方形であることを証明せよ。
【数C】【複素数平面】複素数と図形11 ※問題文は概要欄
単元:
#複素数平面#図形への応用#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
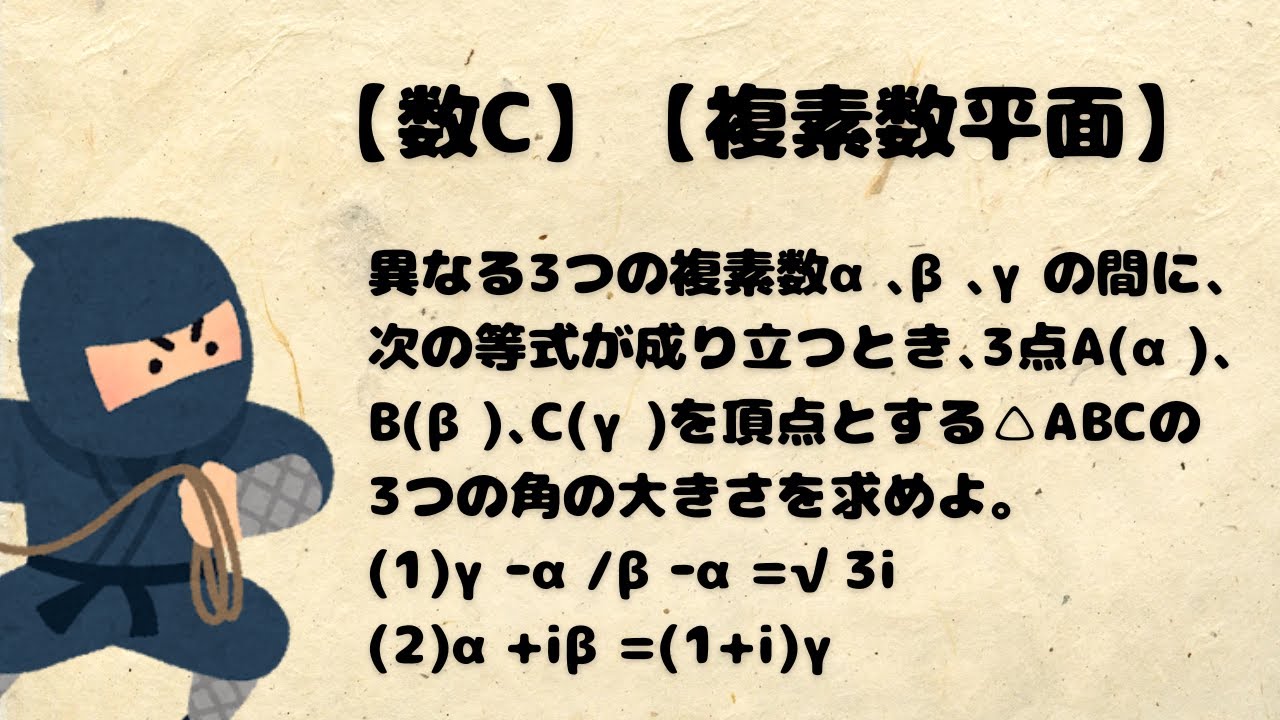
異なる3つの複素数α、β、γの間に、次の等式が成り立つとき、3点A(α)、B(β)、C(γ)を頂点とする△ABCの3つの角の大きさを求めよ。
(1)$\displaystyle \frac{γーα}{βーα}=\sqrt{3}i $
(2)$α+iβ=(1+i)γ$
この動画を見る
異なる3つの複素数α、β、γの間に、次の等式が成り立つとき、3点A(α)、B(β)、C(γ)を頂点とする△ABCの3つの角の大きさを求めよ。
(1)$\displaystyle \frac{γーα}{βーα}=\sqrt{3}i $
(2)$α+iβ=(1+i)γ$
【数C】【複素数平面】複素数と図形10 ※問題文は概要欄
単元:
#複素数平面#図形への応用#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
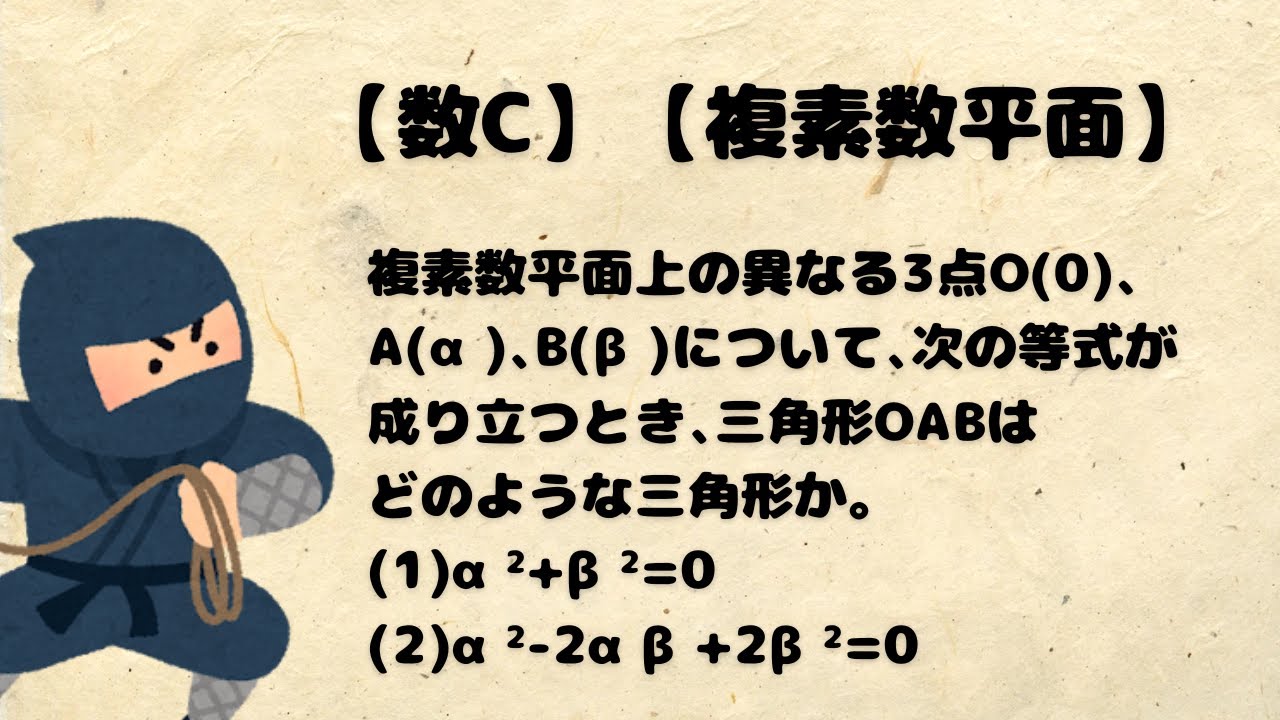
複素数平面上の異なる3点O(0)、A(α)、B(β)について、次の等式が成り立つとき、三角形OABはどのような三角形か。
(1)α²+β²=0
(2)α²-2αβ+2β²=0
この動画を見る
複素数平面上の異なる3点O(0)、A(α)、B(β)について、次の等式が成り立つとき、三角形OABはどのような三角形か。
(1)α²+β²=0
(2)α²-2αβ+2β²=0
【数C】【複素数平面】複素数と図形9 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
複素数平面上の異なる2点A,Bを表す複素数をそれぞれ
1+i、4+3iとする。線分ABを1辺とする正方形の
他の2つの頂点を表す複素数をそれぞれ求めよ。
この動画を見る
複素数平面上の異なる2点A,Bを表す複素数をそれぞれ
1+i、4+3iとする。線分ABを1辺とする正方形の
他の2つの頂点を表す複素数をそれぞれ求めよ。
【受験算数】水90gに食塩10gを溶かし、混ぜ合わせた食塩水100gがあります。この食塩水を40g捨て、水30gを加えて混ぜ合わせました。そこから取り出した食塩水30gには、食塩が何g溶けていますか?

単元:
#算数(中学受験)#文章題#売買損益と食塩水
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
水90gに食塩10gを溶かし、よく混ぜ合わせた食塩水100gがあります。この食塩水を40gくみ出して捨て、そのあと、水30gを加えてよく混ぜ合わせました。
そして、その食塩水を30g取り出しました。取り出した食塩水30gの中には、食塩が何g溶けていますか?
この動画を見る
水90gに食塩10gを溶かし、よく混ぜ合わせた食塩水100gがあります。この食塩水を40gくみ出して捨て、そのあと、水30gを加えてよく混ぜ合わせました。
そして、その食塩水を30g取り出しました。取り出した食塩水30gの中には、食塩が何g溶けていますか?
【数C】【平面上のベクトル】ベクトルの内積1 ※問題文は概要欄

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の条件を満たす2つのベクトル$\vec{ a }$ ,$\vec{ b }$のなす角θを求めよ。
(1) $| \vec{ a } |=2$ ,$|\vec{ b }|=1$ ,$|3\vec{ a }+2\vec{ b } |=2\sqrt{7}$
(2) $| \vec{ a } |=4$ ,$|2\vec{ a } -\vec{ b } |=7$ ,$(\vec{ a } +\vec{ b } )·(\vec{ b } -3\vec{ a } )=-43$
この動画を見る
次の条件を満たす2つのベクトル$\vec{ a }$ ,$\vec{ b }$のなす角θを求めよ。
(1) $| \vec{ a } |=2$ ,$|\vec{ b }|=1$ ,$|3\vec{ a }+2\vec{ b } |=2\sqrt{7}$
(2) $| \vec{ a } |=4$ ,$|2\vec{ a } -\vec{ b } |=7$ ,$(\vec{ a } +\vec{ b } )·(\vec{ b } -3\vec{ a } )=-43$
【受験算数】平面図形総合:相似をつくる

単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の三角形ABCの面積は100cm²で、辺上の各点は、各辺を4等分する点です。 三角形BCDの面積を求めなさい。
この動画を見る
下の三角形ABCの面積は100cm²で、辺上の各点は、各辺を4等分する点です。 三角形BCDの面積を求めなさい。
【日本史探究】日本国憲法第9条

単元:
#社会(高校生)#日本史#近代・現代
指導講師:
理数個別チャンネル
問題文全文(内容文):
理数個別チャンネルの鈴木先生が日本国憲法9条で日本史に頻出な知識をしゃべり倒します!
この動画を見る
理数個別チャンネルの鈴木先生が日本国憲法9条で日本史に頻出な知識をしゃべり倒します!
【受験算数】平面図形総合:折り返す

単元:
#算数(中学受験)#平面図形#平面図形その他
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
たて10cm、横26cmの長方形の形をした紙ABCDを、頂点B が辺AD上に点FにくるようにCEで折り返したところ、 AFの長さが2cmになりました。BEの長さを求めなさい。
この動画を見る
たて10cm、横26cmの長方形の形をした紙ABCDを、頂点B が辺AD上に点FにくるようにCEで折り返したところ、 AFの長さが2cmになりました。BEの長さを求めなさい。
【受験算数】平面図形総合:直角三角形の相似 線分比は?

単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、直角三角形ABCに正方形DEFGがぴったり収まっています。 BE:EF: FCを最も簡単な整数の比で求めなさい。
この動画を見る
図のように、直角三角形ABCに正方形DEFGがぴったり収まっています。 BE:EF: FCを最も簡単な整数の比で求めなさい。
【受験算数】平面図形総合:相似をつくる

単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
四角形ABCDは辺の長さが12cmの正方形で、辺上の各点は、各辺を4等分する点です。斜線部分の面積を求めなさい。
この動画を見る
四角形ABCDは辺の長さが12cmの正方形で、辺上の各点は、各辺を4等分する点です。斜線部分の面積を求めなさい。
【受験算数】平面図形総合:相似を見つける2

単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
高さ7cmの平行四辺形ABCDがあり、ADの長さは10cmです。点Eは辺BC上 の点で、BEの長さは4㎝です。以下の各問いに答えなさい。
(1) AF: FEを最も簡単な整数の比で答えなさい。
(2) AG:GCを最も簡単な整数の比で答えなさい。
(3) 三角形AFGの面積を答えなさい。
この動画を見る
高さ7cmの平行四辺形ABCDがあり、ADの長さは10cmです。点Eは辺BC上 の点で、BEの長さは4㎝です。以下の各問いに答えなさい。
(1) AF: FEを最も簡単な整数の比で答えなさい。
(2) AG:GCを最も簡単な整数の比で答えなさい。
(3) 三角形AFGの面積を答えなさい。
【高校化学】C₆H₁₂Oの化合物の構造決定

単元:
#化学#有機#有機化合物の特徴と構造#有機化合物と人間生活#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
化合物Aは分子式が C₆H₁₂O で, 鏡像異性体が存在する。Aはヨードホルム反応には活性を示すが,フェーリング液を還元しない。 また, Aにナトリウムを加えても,水素は発生しない。化合物Bは分子式がC₆H₁₂O で, 6つの炭素からなる環状の構造をもち, ナトリウムを加えると水素が発生する。Bを濃硫酸と加熱すると, 分子式 C₆H₁₀で表される化合物Cと, 分子式 C₁₂H₂₂O で表される化合物Dが生じた。 次の問いに答えよ。
(1) 化合物Aの構造式を記せ。 ただし, 不斉炭素原子には*印をつけよ。
(2) 化合物 B, C, D の構造式をそれぞれ記せ。
この動画を見る
化合物Aは分子式が C₆H₁₂O で, 鏡像異性体が存在する。Aはヨードホルム反応には活性を示すが,フェーリング液を還元しない。 また, Aにナトリウムを加えても,水素は発生しない。化合物Bは分子式がC₆H₁₂O で, 6つの炭素からなる環状の構造をもち, ナトリウムを加えると水素が発生する。Bを濃硫酸と加熱すると, 分子式 C₆H₁₀で表される化合物Cと, 分子式 C₁₂H₂₂O で表される化合物Dが生じた。 次の問いに答えよ。
(1) 化合物Aの構造式を記せ。 ただし, 不斉炭素原子には*印をつけよ。
(2) 化合物 B, C, D の構造式をそれぞれ記せ。
【高校化学】C₆H₁₀のアルケンの構造決定

単元:
#化学#有機#有機化合物の特徴と構造#有機化合物と人間生活#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の文を読み, 下の各問いに答えよ。
化合物 A~Dは,分子式がいずれも C₆H₁₀の五員環のアルケンである。 AとBは,それぞれ非対称な構造をもち, Aは不斉炭素原子をもつ。 一方, CとDは対称な構造をもつ。A~Dを加熱しながら過マンガン酸カリウムで酸化したところ, A~CはE~Gをそれぞれ生成した。 一方, Dの酸化ではHとIを生成した。 Hはさらに酸化されて二酸化炭素と水になった。 E~Hは酸性を示す化合物であった。 また,Fはヨードホルム反応に陽性でGとIは対称な構造をもつ化合物であった。 二重結合は上のような条件で酸化されると,その二重結合が切れて, カルボニル基に変わる。 生成物がアルデヒドの場合には,さらに酸化されてカルボン酸を生成する。
(1) 化合物 A~I の構造式を記せ。
(2) E~Iの中には, P₄O₁₀と反応して環状化合物およびKをそれぞれ生成するものが見られた。Jは不斉炭素原子をもつが, Kは不斉炭素原子をもたなかった。 またJとKは水と反応すると,もとの構造にもどる性質をもつ。
(i) JおよびKを生成するものはE~I のどれか。 該当するものを記号で答えよ。
(ii) JおよびKの構造式を記せ。
この動画を見る
次の文を読み, 下の各問いに答えよ。
化合物 A~Dは,分子式がいずれも C₆H₁₀の五員環のアルケンである。 AとBは,それぞれ非対称な構造をもち, Aは不斉炭素原子をもつ。 一方, CとDは対称な構造をもつ。A~Dを加熱しながら過マンガン酸カリウムで酸化したところ, A~CはE~Gをそれぞれ生成した。 一方, Dの酸化ではHとIを生成した。 Hはさらに酸化されて二酸化炭素と水になった。 E~Hは酸性を示す化合物であった。 また,Fはヨードホルム反応に陽性でGとIは対称な構造をもつ化合物であった。 二重結合は上のような条件で酸化されると,その二重結合が切れて, カルボニル基に変わる。 生成物がアルデヒドの場合には,さらに酸化されてカルボン酸を生成する。
(1) 化合物 A~I の構造式を記せ。
(2) E~Iの中には, P₄O₁₀と反応して環状化合物およびKをそれぞれ生成するものが見られた。Jは不斉炭素原子をもつが, Kは不斉炭素原子をもたなかった。 またJとKは水と反応すると,もとの構造にもどる性質をもつ。
(i) JおよびKを生成するものはE~I のどれか。 該当するものを記号で答えよ。
(ii) JおよびKの構造式を記せ。
【高校化学】C₁₂H₁₄O₂の芳香族化合物の構造決定

単元:
#化学#有機#有機化合物の特徴と構造#有機化合物と人間生活#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
分子式 C₁₂H₁₄O₂である中性の芳香族化合物Aについて次の実験を行った。 化合物 A~G の構造式を記せ。
実験1 化合物Aを加水分解したのち、 その溶液を酸性にしたところ, C₈H₈O₂の分子式をもつカルボン酸Bと中性の化合物Cを生じた。
実験 2 化合物Cはナトリウムと反応し, 水素を発生した。
実験3 化合物Cは臭素と反応し、臭素が付加した化合物Dを生じた。
実験 4 化合物D は K₂Cr₂O₇ と反応し、中性の化合物Eを生じた。 化合物DおよびEは,いずれもヨードホルム反応に陽性であった。
実験 5 カルボン酸Bを酸化すると, C₈H₆O₄の分子式をもつ化合物F を生じた。 化合物Fを加熱したところ, 分子内で脱水して化合物Gを生じた。
この動画を見る
分子式 C₁₂H₁₄O₂である中性の芳香族化合物Aについて次の実験を行った。 化合物 A~G の構造式を記せ。
実験1 化合物Aを加水分解したのち、 その溶液を酸性にしたところ, C₈H₈O₂の分子式をもつカルボン酸Bと中性の化合物Cを生じた。
実験 2 化合物Cはナトリウムと反応し, 水素を発生した。
実験3 化合物Cは臭素と反応し、臭素が付加した化合物Dを生じた。
実験 4 化合物D は K₂Cr₂O₇ と反応し、中性の化合物Eを生じた。 化合物DおよびEは,いずれもヨードホルム反応に陽性であった。
実験 5 カルボン酸Bを酸化すると, C₈H₆O₄の分子式をもつ化合物F を生じた。 化合物Fを加熱したところ, 分子内で脱水して化合物Gを生じた。
【受験算数】平面図形総合:台形の面積比

単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のような台形ABCDの辺AB上に点Eを、辺DC上に点Fを取ったところ。 EFはADと平行になりました。次の各問いに答えなさい。
(1) EFの長さは何cmですか。
(2) 四角形AEFDと四角形EBCFの面積の・ 比を最も簡単な整数の比で求めなさい。
この動画を見る
図のような台形ABCDの辺AB上に点Eを、辺DC上に点Fを取ったところ。 EFはADと平行になりました。次の各問いに答えなさい。
(1) EFの長さは何cmですか。
(2) 四角形AEFDと四角形EBCFの面積の・ 比を最も簡単な整数の比で求めなさい。
【受験算数】平面図形総合:平行四辺形の面積比2

単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
四角形ABCDは平行四辺形で、辺上の各点は、辺ADを4等分する点、辺BC を5等分する点です。平行四辺形ABCDの面積と斜線部分の面積の池を最も簡単 な整数の比で求めなさい。
この動画を見る
四角形ABCDは平行四辺形で、辺上の各点は、辺ADを4等分する点、辺BC を5等分する点です。平行四辺形ABCDの面積と斜線部分の面積の池を最も簡単 な整数の比で求めなさい。
【受験算数】平面図形総合:相似な図形を見つける1

単元:
#算数(中学受験)#平面図形#相似と相似を利用した問題
指導講師:
理数個別チャンネル
問題文全文(内容文):
四角形$\rm ABCD$は長方形で、$\rm AB=7\,cm$、$\rm AD=50\,cm$です。点$\rm E$は辺$\rm BC$上の点で、 $\rm BE=2\,cm$、点$\rm F$は辺$\rm CD$上の点で、$\rm DF=3\,cm$です。次の各問いに答えなさい。
(1) $\rm AG:GE$を最も簡単な無数の比で答えなさい。
(2) $\rm AH: HF$を最も簡単な整数の比で答えなさい。
(3) 五角形$\rm GECFH$の面積を答えなさい
この動画を見る
四角形$\rm ABCD$は長方形で、$\rm AB=7\,cm$、$\rm AD=50\,cm$です。点$\rm E$は辺$\rm BC$上の点で、 $\rm BE=2\,cm$、点$\rm F$は辺$\rm CD$上の点で、$\rm DF=3\,cm$です。次の各問いに答えなさい。
(1) $\rm AG:GE$を最も簡単な無数の比で答えなさい。
(2) $\rm AH: HF$を最も簡単な整数の比で答えなさい。
(3) 五角形$\rm GECFH$の面積を答えなさい
【数B】【数列】自然数の式の証明3 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
$n$は自然数とする。
$6^n+4= (5+1)^n+4$と変形することで、$6^n+4$が$5$の倍数であることを、二項定理を利用して証明せよ。
この動画を見る
$n$は自然数とする。
$6^n+4= (5+1)^n+4$と変形することで、$6^n+4$が$5$の倍数であることを、二項定理を利用して証明せよ。
【数B】【数列】自然数の式の証明2 ※問題文は概要欄

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
$n$は整数とする。
(1)連続する2個の整数には、必ず$2$の倍数が含まれることを利用して、 $n^2+3n$が$2$の倍数であることを証明せよ。
(2)連続する3個の整数には、必ず$3$の倍数が含まれることを利用して、 $4n^3+3n^2+2n$が$3$の倍数であることを証明せよ。
この動画を見る
$n$は整数とする。
(1)連続する2個の整数には、必ず$2$の倍数が含まれることを利用して、 $n^2+3n$が$2$の倍数であることを証明せよ。
(2)連続する3個の整数には、必ず$3$の倍数が含まれることを利用して、 $4n^3+3n^2+2n$が$3$の倍数であることを証明せよ。




