 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【数Ⅱ】【三角関数】三角関数の合成6 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数 y=asinx+bcosxはx=$\frac{π}{6}$で最大値をとり, また, 最小値 -5である。定数a,bの値を求めよ。
この動画を見る
関数 y=asinx+bcosxはx=$\frac{π}{6}$で最大値をとり, また, 最小値 -5である。定数a,bの値を求めよ。
【数Ⅱ】【三角関数】三角関数の合成5 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数の最大値, 最小値と, そのときのxの値も求めよ。
y=2sin$^{2}$x+2$\sqrt{3}$sinxcosx+4cos$^{2}$x (0$\leqq$x$\lt$2π)
この動画を見る
次の関数の最大値, 最小値と, そのときのxの値も求めよ。
y=2sin$^{2}$x+2$\sqrt{3}$sinxcosx+4cos$^{2}$x (0$\leqq$x$\lt$2π)
【数Ⅱ】【三角関数】三角関数の合成4 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
0$\leqq$x$\leqq$πのとき、次の関数の最大値, 最小値を求めよ。(1)については、そのときのxの値も求めよ。
(1) y=sinx+$\sqrt{3}$cosx
(2) y=2sinx+cosx
この動画を見る
0$\leqq$x$\leqq$πのとき、次の関数の最大値, 最小値を求めよ。(1)については、そのときのxの値も求めよ。
(1) y=sinx+$\sqrt{3}$cosx
(2) y=2sinx+cosx
【数Ⅱ】【三角関数】三角関数の合成3 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数の最大値, 最小値を求めよ。(1),(2)については、そのときのxの値も求めよ。
(1) y=-sinx+cosx(0$\leqq$x$\lt$2π)
(2) y=sin2x-$\sqrt{3}$cos2x(0$\leqq$x$\lt$π)
(3) y=4sinx+3cosx
(4) y=$\sqrt{7}$sinx-3cosx
この動画を見る
次の関数の最大値, 最小値を求めよ。(1),(2)については、そのときのxの値も求めよ。
(1) y=-sinx+cosx(0$\leqq$x$\lt$2π)
(2) y=sin2x-$\sqrt{3}$cos2x(0$\leqq$x$\lt$π)
(3) y=4sinx+3cosx
(4) y=$\sqrt{7}$sinx-3cosx
【数Ⅱ】【三角関数】三角関数の合成2 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
0$\leqq$x$\lt$2πのとき、次の不等式を解け。
(1) sinx+cosx$\geqq$$\frac{1}{\sqrt{2} }$
(2) cosx$\lt$$\sqrt{3}$sinx
(3) $\sqrt{2}$$\leqq$sinx-$\sqrt{3}$cosx$\lt$$\sqrt{3}$
この動画を見る
0$\leqq$x$\lt$2πのとき、次の不等式を解け。
(1) sinx+cosx$\geqq$$\frac{1}{\sqrt{2} }$
(2) cosx$\lt$$\sqrt{3}$sinx
(3) $\sqrt{2}$$\leqq$sinx-$\sqrt{3}$cosx$\lt$$\sqrt{3}$
【数Ⅱ】【三角関数】三角関数の合成1 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
0$\leqq$x$\lt$2πのとき、次の方程式を解け。
(1) $sinx+\sqrt{3}cosx=-1$
(2) $2(sinx-cosx)=\sqrt{6}$
(3) $\sqrt{3}sin2x-cos2x=-\sqrt{2}$
この動画を見る
0$\leqq$x$\lt$2πのとき、次の方程式を解け。
(1) $sinx+\sqrt{3}cosx=-1$
(2) $2(sinx-cosx)=\sqrt{6}$
(3) $\sqrt{3}sin2x-cos2x=-\sqrt{2}$
【数Ⅱ】【三角関数】加法定理の応用7 ※問題文は概要欄
単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
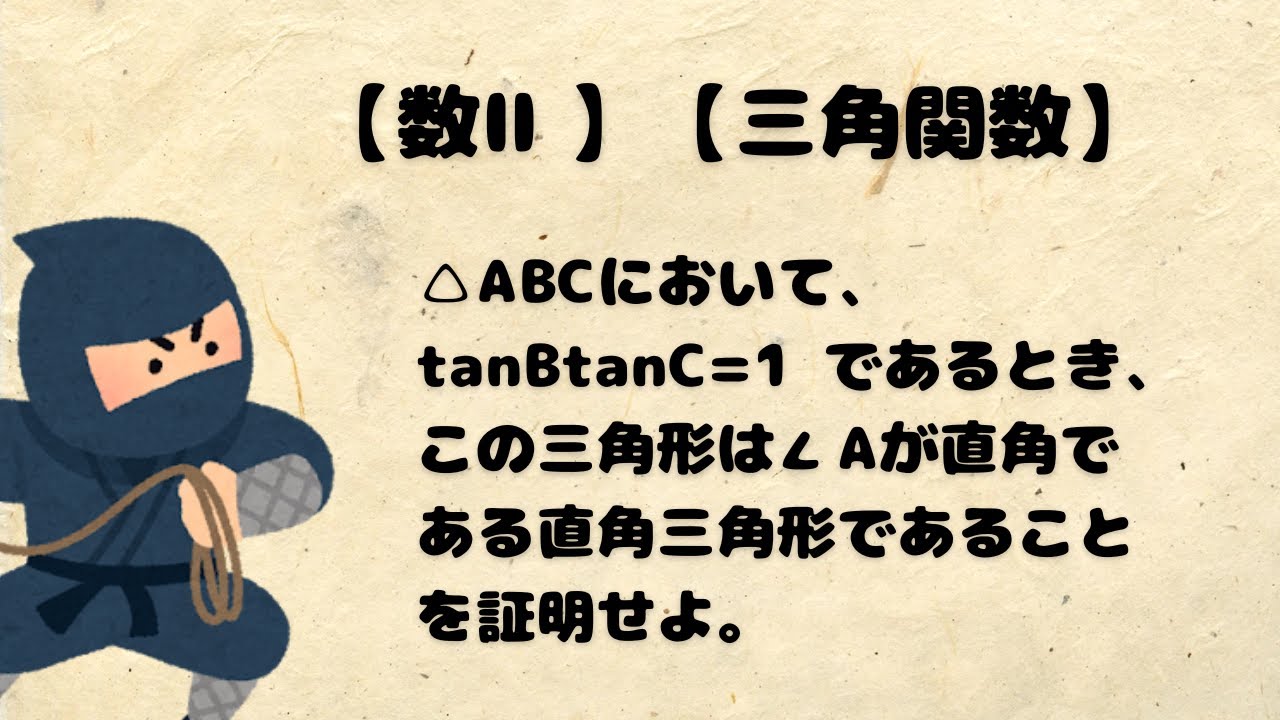
△ABCにおいて、 tanBtanC=1 であるとき、この三角形は∠Aが直角である直角三角形であることを証明せよ。
この動画を見る
△ABCにおいて、 tanBtanC=1 であるとき、この三角形は∠Aが直角である直角三角形であることを証明せよ。
【数Ⅱ】【三角関数】加法定理の応用6 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数のグラフをかけ。また、その周期をいえ。
(1) y=cos² x
(2) y=3sin² x+cos² x
この動画を見る
次の関数のグラフをかけ。また、その周期をいえ。
(1) y=cos² x
(2) y=3sin² x+cos² x
【数Ⅱ】【三角関数】加法定理の応用5 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
-π/2≦x≦π/2 とする。関数 y=2sinx-cos2x の最大値、最小値と、そのときのxの値を求めよ。
この動画を見る
-π/2≦x≦π/2 とする。関数 y=2sinx-cos2x の最大値、最小値と、そのときのxの値を求めよ。
【数Ⅱ】【三角関数】加法定理の応用4 ※問題文は概要欄
単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
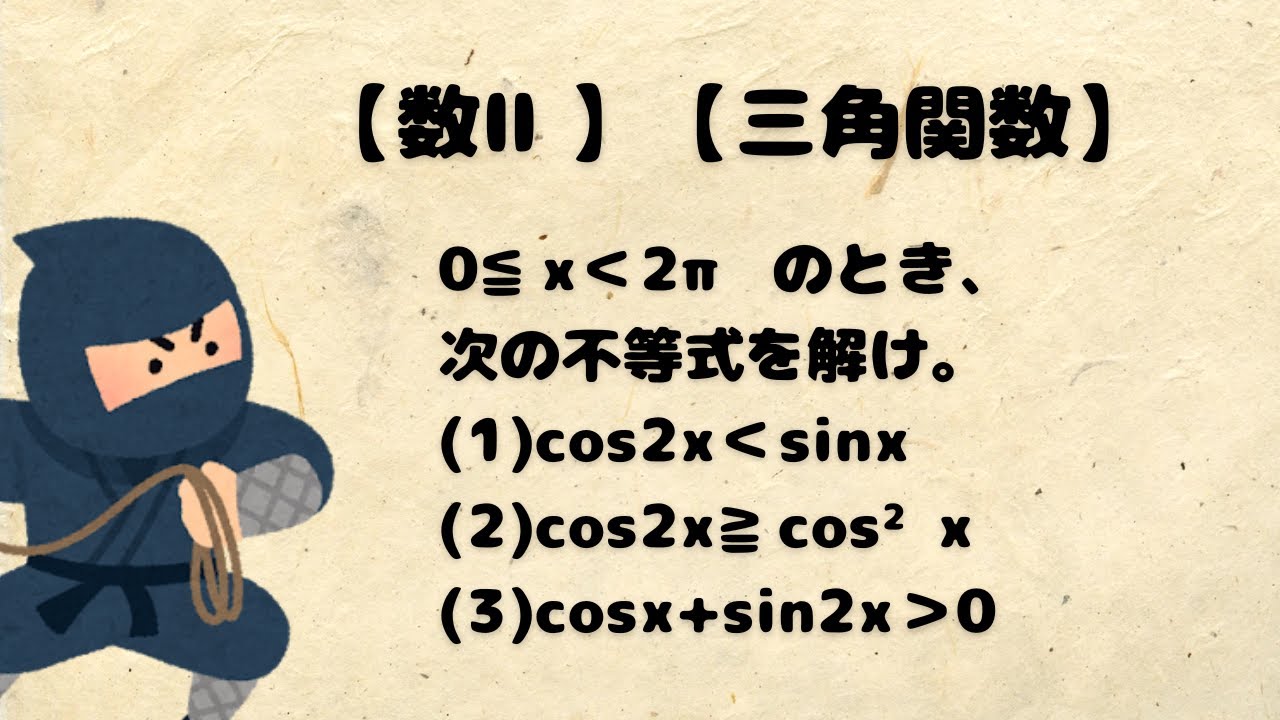
0≦x<2π のとき、次の不等式を解け。
(1)cos2x<sinx
(2)cos2x≧cos² x
(3)cosx+sin2x>0
この動画を見る
0≦x<2π のとき、次の不等式を解け。
(1)cos2x<sinx
(2)cos2x≧cos² x
(3)cosx+sin2x>0
【数Ⅱ】【三角関数】加法定理の応用3 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
0≦x<2π のとき、次の方程式を解け。
(1)cos2x=cosx
(2)sin2x=cosx
(3)2cos2x+4cosx-1=0
(4)sinx(1+cos2x)+sin2x(1+cosx)=0
この動画を見る
0≦x<2π のとき、次の方程式を解け。
(1)cos2x=cosx
(2)sin2x=cosx
(3)2cos2x+4cosx-1=0
(4)sinx(1+cos2x)+sin2x(1+cosx)=0
【数Ⅱ】【三角関数】加法定理の応用2 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
tanα=t のときcos² α ,sin2α ,cos2α を t で表せ。
この動画を見る
tanα=t のときcos² α ,sin2α ,cos2α を t で表せ。
【数Ⅱ】【三角関数】加法定理の応用1 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
等式cos3α+sin3α=(cosα-sinα)(1+2sin2α)を証明せよ。
この動画を見る
等式cos3α+sin3α=(cosα-sinα)(1+2sin2α)を証明せよ。
【数Ⅲ】【積分とその応用】定積分部分積分 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
定積分$\displaystyle \int_0^1x^2e^{2x}~dx$を求めよ。
定積分$\displaystyle \int_0^\frac\pi2(ax-\sin x)^2~dx$を最小にする実数$a$の値を求めよ。
定積分$\displaystyle I=\int_0^\frac\pi2e^{-3x}\sin x~dx$を求めよ。
自然数$n$について、$\displaystyle I_n=\int_1^e(\log x)^n~dx$とする。
(1) $I_1$を求めよ。
(2) $I_{n+1}$を$I_n$を用いて表せ。
(3) $I_4$を求めよ。
この動画を見る
定積分$\displaystyle \int_0^1x^2e^{2x}~dx$を求めよ。
定積分$\displaystyle \int_0^\frac\pi2(ax-\sin x)^2~dx$を最小にする実数$a$の値を求めよ。
定積分$\displaystyle I=\int_0^\frac\pi2e^{-3x}\sin x~dx$を求めよ。
自然数$n$について、$\displaystyle I_n=\int_1^e(\log x)^n~dx$とする。
(1) $I_1$を求めよ。
(2) $I_{n+1}$を$I_n$を用いて表せ。
(3) $I_4$を求めよ。
【数Ⅲ】【積分とその応用】定積分置換積分 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の定積分を求めよ。
(1) $\displaystyle \int_{-1}^0 (x+2)\sqrt{3x+4}~dx$
(2) $\displaystyle \int_{0}^4 \frac{x^2}{\sqrt{x+1}}~dx$
(3) $\displaystyle \int_{0}^1 \frac{x^3}{\sqrt{1+x^2}}~dx$
(4) $\displaystyle \int_{1}^3 \frac{dx}{x\sqrt{x+1}}$
(5) $\displaystyle \int_{1}^2 \frac{dx}{e^x-1}$
(6) $\displaystyle \int_{0}^{\frac\pi4} \frac{\sin^3x}{\cos^2x}~dx$
次の定積分を求めよ。ただし、$a$は正の定数とする。
(1) $\displaystyle \int_{0}^1 \sqrt{2x-x^2}~dx$
(2) $\displaystyle \int_{1}^{\frac12} \frac{dx}{\sqrt{2x-x^2}}$
(3) $\displaystyle \int_{1}^{\frac a2} \frac{dx}{(a^2-x^2)^{\frac32}}$
(4) $\displaystyle \int_{1}^{2} \frac{dx}{x^2-2x+2}$
(5) $\displaystyle \int_{3}^{5} \frac{dx}{x^2-4x+4}$
(6) $\displaystyle \int_{6}^{12} \frac{dx}{x^2-3x-10}$
(7) $\displaystyle \int_{0}^{a} \frac{dx}{(x^2+a^2)^2}$
(8) $\displaystyle \int_{1}^{\sqrt3} \frac{2x+1}{x^2+1}~dx$
次のことが成り立つことを証明せよ。
(1) $\displaystyle \int_a^b f(x)~dx=\int_a^bf(a+b-x)~dx$
(2) $\displaystyle\int_{-a}^af(x)~dx=\int_0^a\{f(x)+f(-x)\}~dx$
(3) $\displaystyle \int_0^af(x)~dx=\int_0^{\frac a 2}\{f(x)+f(a-x)\}~dx$
(4) $f(a+x)=f(a-x)$のとき$\displaystyle \int_{a-b}^{a+b}f(x)~dx=2\int_a^{a+b}f(x)~dx$
この動画を見る
次の定積分を求めよ。
(1) $\displaystyle \int_{-1}^0 (x+2)\sqrt{3x+4}~dx$
(2) $\displaystyle \int_{0}^4 \frac{x^2}{\sqrt{x+1}}~dx$
(3) $\displaystyle \int_{0}^1 \frac{x^3}{\sqrt{1+x^2}}~dx$
(4) $\displaystyle \int_{1}^3 \frac{dx}{x\sqrt{x+1}}$
(5) $\displaystyle \int_{1}^2 \frac{dx}{e^x-1}$
(6) $\displaystyle \int_{0}^{\frac\pi4} \frac{\sin^3x}{\cos^2x}~dx$
次の定積分を求めよ。ただし、$a$は正の定数とする。
(1) $\displaystyle \int_{0}^1 \sqrt{2x-x^2}~dx$
(2) $\displaystyle \int_{1}^{\frac12} \frac{dx}{\sqrt{2x-x^2}}$
(3) $\displaystyle \int_{1}^{\frac a2} \frac{dx}{(a^2-x^2)^{\frac32}}$
(4) $\displaystyle \int_{1}^{2} \frac{dx}{x^2-2x+2}$
(5) $\displaystyle \int_{3}^{5} \frac{dx}{x^2-4x+4}$
(6) $\displaystyle \int_{6}^{12} \frac{dx}{x^2-3x-10}$
(7) $\displaystyle \int_{0}^{a} \frac{dx}{(x^2+a^2)^2}$
(8) $\displaystyle \int_{1}^{\sqrt3} \frac{2x+1}{x^2+1}~dx$
次のことが成り立つことを証明せよ。
(1) $\displaystyle \int_a^b f(x)~dx=\int_a^bf(a+b-x)~dx$
(2) $\displaystyle\int_{-a}^af(x)~dx=\int_0^a\{f(x)+f(-x)\}~dx$
(3) $\displaystyle \int_0^af(x)~dx=\int_0^{\frac a 2}\{f(x)+f(a-x)\}~dx$
(4) $f(a+x)=f(a-x)$のとき$\displaystyle \int_{a-b}^{a+b}f(x)~dx=2\int_a^{a+b}f(x)~dx$
【数Ⅲ】【積分とその応用】定積分置換積分、部分積分 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次を求めよ
(1) $\displaystyle \int_0^1 \sqrt{e^{1-t}}~dt$
(2) $\displaystyle \int_0^{\frac{\pi}2}\frac{\cos{2\theta}}{\sin \theta+\cos\theta}~d\theta$
(3) $\displaystyle\int_0^\pi \sin^4x~dx$
(4) $\displaystyle \int_1^2 \frac{\sqrt{x^2-4x+4}}{x}~dx$
次を求めよ
(1) $\displaystyle \int_0^\pi |\cos2\theta|~d\theta$
(2) $\displaystyle \int_0^\pi|\sin x+\cos x|~dx$
$m,n$は正の整数とする。次の定積分を求めよ。
(1) $\displaystyle \int_0^\pi \cos mx\cos nx~dx$
(2) $\displaystyle \int_0^\pi \sin mx\sin nx~dx$
(3) $\displaystyle \int_0^\pi \sin mx\cos nx~dx$
定積分$\displaystyle \int_0^\pi (1-a\sin x-b\sin2x)^2~dx$を最小にする定数$a,b$の値を求めよ。
この動画を見る
次を求めよ
(1) $\displaystyle \int_0^1 \sqrt{e^{1-t}}~dt$
(2) $\displaystyle \int_0^{\frac{\pi}2}\frac{\cos{2\theta}}{\sin \theta+\cos\theta}~d\theta$
(3) $\displaystyle\int_0^\pi \sin^4x~dx$
(4) $\displaystyle \int_1^2 \frac{\sqrt{x^2-4x+4}}{x}~dx$
次を求めよ
(1) $\displaystyle \int_0^\pi |\cos2\theta|~d\theta$
(2) $\displaystyle \int_0^\pi|\sin x+\cos x|~dx$
$m,n$は正の整数とする。次の定積分を求めよ。
(1) $\displaystyle \int_0^\pi \cos mx\cos nx~dx$
(2) $\displaystyle \int_0^\pi \sin mx\sin nx~dx$
(3) $\displaystyle \int_0^\pi \sin mx\cos nx~dx$
定積分$\displaystyle \int_0^\pi (1-a\sin x-b\sin2x)^2~dx$を最小にする定数$a,b$の値を求めよ。
【数Ⅲ】【積分とその応用】不定積分置換積分、部分積分3 ※問題文は概要欄

単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{\sqrt x}{\sqrt[4]{x^3}+1}~dx$
(2) $\displaystyle \int \frac{dx}{x\sqrt{x+1}}$
(3) $\displaystyle \int \log|x^2-1|~dx$
(4) $\displaystyle \int \frac{e^x}{e^x-e^{-x}}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \tan^4x~dx$
(2) $\displaystyle \int \frac{dx}{\sin{2x}}$
(3) $\displaystyle \int \frac{1}{1-\sin x}~dx$
(4) $\displaystyle \int (\sin^3x-\cos^3x)~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int e^x\cos x~dx$
(2) $\displaystyle \int e^{-x}\sin x~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \sin x\log(\cos x)~dx$
(2) $\displaystyle \int x\tan^2x~dx$
(3) $\displaystyle \int \frac{1}{1-e^x}~dx$
この動画を見る
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{\sqrt x}{\sqrt[4]{x^3}+1}~dx$
(2) $\displaystyle \int \frac{dx}{x\sqrt{x+1}}$
(3) $\displaystyle \int \log|x^2-1|~dx$
(4) $\displaystyle \int \frac{e^x}{e^x-e^{-x}}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \tan^4x~dx$
(2) $\displaystyle \int \frac{dx}{\sin{2x}}$
(3) $\displaystyle \int \frac{1}{1-\sin x}~dx$
(4) $\displaystyle \int (\sin^3x-\cos^3x)~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int e^x\cos x~dx$
(2) $\displaystyle \int e^{-x}\sin x~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \sin x\log(\cos x)~dx$
(2) $\displaystyle \int x\tan^2x~dx$
(3) $\displaystyle \int \frac{1}{1-e^x}~dx$
【数Ⅲ】【積分とその応用】不定積分置換積分、部分積分2 ※問題文は概要欄

単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{x^2+x+1}{x^2+1}~dx$
(2) $\displaystyle \int \frac{x^4}{x^2-1}~dx$
(1)次の等式が成り立つように、定数$a,b,c$の値を定めよ。
$\dfrac{3x+2}{x(x+1)^2}=\dfrac{a}{x}+\dfrac{b}{x+1}+\dfrac{c}{(x+1)^2}$
(2)不定積分$\displaystyle \int \dfrac{3x+2}{x(x+1)^2}~dx$を求めよ。
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{dx}{x(x^2-1)}$
(2) $\displaystyle \int \frac{dx}{x^2(x+2)}$
(3) $\displaystyle \int \frac{dx}{x(x^2+1)}$
(4) $\displaystyle \int \frac{x^2+1}{x^4-5x^2+4}~dx$
(5) $\displaystyle \int \frac{3x+2}{x(x+1)^3}~dx$
(6) $\displaystyle \int \frac{x^4}{x^3-3x+2}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{dx}{\sqrt{x+1}-\sqrt x}$
(2) $\displaystyle \int \frac{x}{\sqrt{3x+4}-2}~dx$
この動画を見る
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{x^2+x+1}{x^2+1}~dx$
(2) $\displaystyle \int \frac{x^4}{x^2-1}~dx$
(1)次の等式が成り立つように、定数$a,b,c$の値を定めよ。
$\dfrac{3x+2}{x(x+1)^2}=\dfrac{a}{x}+\dfrac{b}{x+1}+\dfrac{c}{(x+1)^2}$
(2)不定積分$\displaystyle \int \dfrac{3x+2}{x(x+1)^2}~dx$を求めよ。
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{dx}{x(x^2-1)}$
(2) $\displaystyle \int \frac{dx}{x^2(x+2)}$
(3) $\displaystyle \int \frac{dx}{x(x^2+1)}$
(4) $\displaystyle \int \frac{x^2+1}{x^4-5x^2+4}~dx$
(5) $\displaystyle \int \frac{3x+2}{x(x+1)^3}~dx$
(6) $\displaystyle \int \frac{x^4}{x^3-3x+2}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{dx}{\sqrt{x+1}-\sqrt x}$
(2) $\displaystyle \int \frac{x}{\sqrt{3x+4}-2}~dx$
【小6算数手元解説】図書館の本を1年生、2年生、3年生で整理する。 【問題文は概要欄】

単元:
#算数(中学受験)#文章題#仕事算とニュートン算
教材:
#マスターテキスト#中学受験教材#小6 サマーサポート
指導講師:
理数個別チャンネル
問題文全文(内容文):
図書館の本の半分を整理するのに1年生6人ですると9日間、2年生9人ですると4日間、3年生3人ですると9日間かかります。1年生5人,2年生2人, 3年生2人の3学年でいっしょに図書館のすべての本を整理すると何日かかりますか。ただし、同じ学年の生徒1人あたりの1日に整理できる本の量は同じであるとします。
この動画を見る
図書館の本の半分を整理するのに1年生6人ですると9日間、2年生9人ですると4日間、3年生3人ですると9日間かかります。1年生5人,2年生2人, 3年生2人の3学年でいっしょに図書館のすべての本を整理すると何日かかりますか。ただし、同じ学年の生徒1人あたりの1日に整理できる本の量は同じであるとします。
【数Ⅲ】【積分とその応用】不定積分置換積分、部分積分1 ※問題文は概要欄

単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不定積分を求めよ。
(1) $\displaystyle \int x\sqrt[3]{1+x}~dx$
(2) $\displaystyle \int \sin x \cos^4x~dx$
(3) $\displaystyle \int \frac {dx}{\cos^4x}$
(4) $\displaystyle \int (2x+1)e^{x^2+x+5}~dx$
(5) $\displaystyle \int \frac{e^{2x}}{(e^x+2)^2}~dx$
(6) $\displaystyle \int \frac{\log x}{x(\log x-1)^2}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{x}{\cos^2x}~dx$
(2) $\displaystyle \int x\log(x-2)~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int x\log(x^2-2)~dx$
(2) $\displaystyle \int e^x\log(e^x+1)~dx$
不定積分$\displaystyle \int (\log x)^3~dx$を求めよ。
この動画を見る
次の不定積分を求めよ。
(1) $\displaystyle \int x\sqrt[3]{1+x}~dx$
(2) $\displaystyle \int \sin x \cos^4x~dx$
(3) $\displaystyle \int \frac {dx}{\cos^4x}$
(4) $\displaystyle \int (2x+1)e^{x^2+x+5}~dx$
(5) $\displaystyle \int \frac{e^{2x}}{(e^x+2)^2}~dx$
(6) $\displaystyle \int \frac{\log x}{x(\log x-1)^2}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{x}{\cos^2x}~dx$
(2) $\displaystyle \int x\log(x-2)~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int x\log(x^2-2)~dx$
(2) $\displaystyle \int e^x\log(e^x+1)~dx$
不定積分$\displaystyle \int (\log x)^3~dx$を求めよ。
【数Ⅱ】【微分法と積分法】接線からの関数決定 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$f'(x)=x^2+2x+2$で、曲線$y=f(x)$は$y=-3x+1$に接している。この時、$f(x)$を求めよ。
この動画を見る
$f'(x)=x^2+2x+2$で、曲線$y=f(x)$は$y=-3x+1$に接している。この時、$f(x)$を求めよ。
【数Ⅱ】【微分法と積分法】係数比較から関数の決定 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2次関数$f(x)$の1つの不定積分$F(x)$が$xf(x)-2x^3+3x^2$に等しく、$f(1)=0$であるとき、$f(x)$を求めよ。
この動画を見る
2次関数$f(x)$の1つの不定積分$F(x)$が$xf(x)-2x^3+3x^2$に等しく、$f(1)=0$であるとき、$f(x)$を求めよ。
【小6算数手元解説】受験算数 上・中・下巻 それぞれ何ページ 【問題文は概要欄】

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#文章題その他
教材:
#マスターテキスト#中学受験教材#小6 サマーサポート
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある小説は、上、中、下の3巻に分けて出版されています。ただし、内容上きりのよいところでわけられているため、各巻が同じページ数とは限りません。中巻は上巻より20ページ多くなっています。
まさる君は、この小説を読んでいるとき、中巻のページ数の60%まで読んだところで、全体のページ数でも60%読んだことになると気がつきました。また、下巻の16ページを読み終えたところで、全体のページ数の80%を読み終えたことにも気がつきました。
各巻のページ数を求めなさい。
この動画を見る
ある小説は、上、中、下の3巻に分けて出版されています。ただし、内容上きりのよいところでわけられているため、各巻が同じページ数とは限りません。中巻は上巻より20ページ多くなっています。
まさる君は、この小説を読んでいるとき、中巻のページ数の60%まで読んだところで、全体のページ数でも60%読んだことになると気がつきました。また、下巻の16ページを読み終えたところで、全体のページ数の80%を読み終えたことにも気がつきました。
各巻のページ数を求めなさい。
【小6算数手元解説】受験算数 最初にもっていた金額と等しくなる【問題文は概要欄】

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#文章題その他
教材:
#マスターテキスト#中学受験教材#小6 サマーサポート
指導講師:
理数個別チャンネル
問題文全文(内容文):
A,B,C,D,Eがいくらかずつお金を持っています。AとEの持っている金額は等しく、A,B,C,Dの持っている金額にそれぞれ100円、200円、300円、400円を加えると、それぞれA,B,C,D,Eが最初に持っていた金額の合計の1/12、1/6、1/4、1/2に等しくなります。A,B,C,Dは最初いくらずつ持っていましたか。
この動画を見る
A,B,C,D,Eがいくらかずつお金を持っています。AとEの持っている金額は等しく、A,B,C,Dの持っている金額にそれぞれ100円、200円、300円、400円を加えると、それぞれA,B,C,D,Eが最初に持っていた金額の合計の1/12、1/6、1/4、1/2に等しくなります。A,B,C,Dは最初いくらずつ持っていましたか。
【小6算数手元解説】受験算数 ある本を読んで全体の7分の2残った【問題文は概要欄】

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
教材:
#マスターテキスト#中学受験教材#小6 サマーサポート
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある1冊の本を読みました。1日目に55ページを読み、2日目に残りの9分の5よりも20ページだけ多くの部分を読んだところ、残っていたのは、その本の7分の2でした。この本は全部で何ページありますか。
この動画を見る
ある1冊の本を読みました。1日目に55ページを読み、2日目に残りの9分の5よりも20ページだけ多くの部分を読んだところ、残っていたのは、その本の7分の2でした。この本は全部で何ページありますか。
【数C】【複素数平面】複素数と図形8 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
複素数平面上の2点$\rm A,B$を表す複素数をそれぞれ$\alpha=1-2i,\beta=3+2i$とするとき
線分$\rm AB$を1辺とする正三角形の他の頂点$\rm C$を表す複素数$\gamma$を求めよ。
この動画を見る
複素数平面上の2点$\rm A,B$を表す複素数をそれぞれ$\alpha=1-2i,\beta=3+2i$とするとき
線分$\rm AB$を1辺とする正三角形の他の頂点$\rm C$を表す複素数$\gamma$を求めよ。
【数C】【複素数平面】複素数と図形7 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
原点を${\rm {O}}, \alpha=2-i,\beta=3+(2a-1)i$を表す点をそれぞれ$\rm A,B$とするとき、$\rm \angle AOB=\dfrac\pi4$を満たす実数$a$の値を求めよ。
この動画を見る
原点を${\rm {O}}, \alpha=2-i,\beta=3+(2a-1)i$を表す点をそれぞれ$\rm A,B$とするとき、$\rm \angle AOB=\dfrac\pi4$を満たす実数$a$の値を求めよ。
【数C】【複素数平面】複素数と図形6 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
複素数平面上の異なる4点$\rm A(\alpha),B(\beta),C(\gamma),D(\delta)$
について次のことが成り立つことを証明せよ。
2直線$\rm AB,CD$が垂直に交わる ⇔ $\dfrac{(\delta-\gamma)}{(\beta-\alpha)}$が純虚数
この動画を見る
複素数平面上の異なる4点$\rm A(\alpha),B(\beta),C(\gamma),D(\delta)$
について次のことが成り立つことを証明せよ。
2直線$\rm AB,CD$が垂直に交わる ⇔ $\dfrac{(\delta-\gamma)}{(\beta-\alpha)}$が純虚数
【数C】【複素数平面】複素数と図形5 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
点$z$が、点$-1$を通り実軸に垂直な直線上を動くとき、
点$w=\dfrac1z$ はどのような図形を描くか。
この動画を見る
点$z$が、点$-1$を通り実軸に垂直な直線上を動くとき、
点$w=\dfrac1z$ はどのような図形を描くか。
【数C】【複素数平面】複素数と図形4 ※問題文は概要欄

単元:
#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
点$z$が、原点$\rm O$を中心とする半径1の円から$-1$を除いた図形上を動くとき、
点$w=\dfrac {(z+i)}{(z+1)}$はどのような図形を描くか。
この動画を見る
点$z$が、原点$\rm O$を中心とする半径1の円から$-1$を除いた図形上を動くとき、
点$w=\dfrac {(z+i)}{(z+1)}$はどのような図形を描くか。




