 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【数学】中高一貫校問題集2幾何120:円:円の接線:内心の性質
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
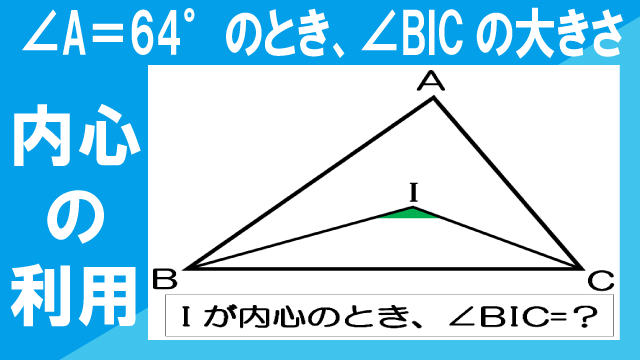
△ABCの内心をIとする。∠A=64°のとき、∠BICの大きさを求めなさい。
この動画を見る
△ABCの内心をIとする。∠A=64°のとき、∠BICの大きさを求めなさい。
【数学】中高一貫校問題集2幾何119:円:円の接線:円外から引いた接線の長さは同じ
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
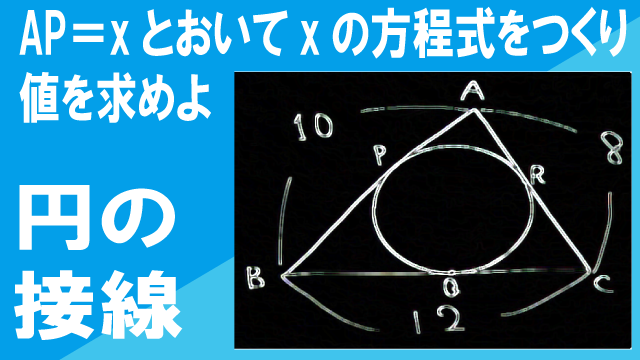
図のように、△ABCの内接円が、辺AB、BC、CA、と接する点を、それぞれP、Q、Rとする。また、AB=10、BC=12、CA=8とする。AP=xとおいてxの方程式をつくり、それを解いてxの値を求めなさい。
この動画を見る
図のように、△ABCの内接円が、辺AB、BC、CA、と接する点を、それぞれP、Q、Rとする。また、AB=10、BC=12、CA=8とする。AP=xとおいてxの方程式をつくり、それを解いてxの値を求めなさい。
【3日目】毎日3分古文単語【13~18】【55日間完成】

単元:
#国語(高校生)#古文#単語
教材:
#中高教材#古文単語330三訂版-いいずな書店#単語帳
指導講師:
理数個別チャンネル
問題文全文(内容文):
<今日の単語>
13.かなし(2)
14.いみじ(3)
15.をかし(3)
16.よし(2)
17.あやし(4)
18.おとなし(3)
この動画を見る
<今日の単語>
13.かなし(2)
14.いみじ(3)
15.をかし(3)
16.よし(2)
17.あやし(4)
18.おとなし(3)
【数学】中高一貫校問題集2幾何118:円:円の接線:弧の比=中心角 or 円周角
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
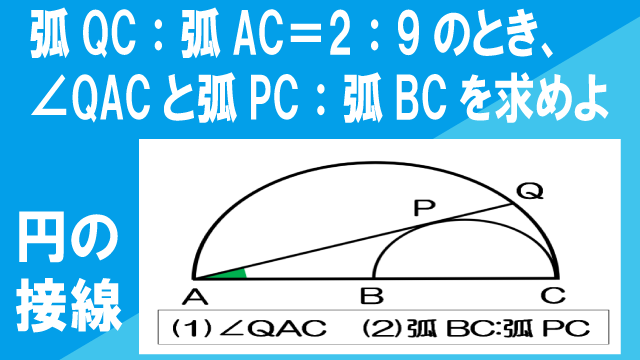
右の図のように、AC、BCを直径とする2つの半径において、大きい半円弦AQは小さい半円に点Pで接している。弧QC:弧AC=2:9のとき、次の問いに答えなさい。
(1)∠QACの大きさを求めなさい。
(2)弧PC:弧BCを求めなさい。
この動画を見る
右の図のように、AC、BCを直径とする2つの半径において、大きい半円弦AQは小さい半円に点Pで接している。弧QC:弧AC=2:9のとき、次の問いに答えなさい。
(1)∠QACの大きさを求めなさい。
(2)弧PC:弧BCを求めなさい。
【2日目】毎日3分古文単語【7~12】【55日間完成】

単元:
#国語(高校生)#古文#単語
教材:
#中高教材#古文単語330三訂版-いいずな書店#単語帳
指導講師:
理数個別チャンネル
問題文全文(内容文):
<今日の単語>
7.みゆ(3)
8.あふ(1)
9.ゐる(2)
10.ありく(3)
11.あく(2)
12.うつくし(2)
この動画を見る
<今日の単語>
7.みゆ(3)
8.あふ(1)
9.ゐる(2)
10.ありく(3)
11.あく(2)
12.うつくし(2)
【1日目】毎日3分古文単語【1~6】【55日間完成】

単元:
#古文#単語
教材:
#中高教材#古文単語330三訂版-いいずな書店#単語帳
指導講師:
理数個別チャンネル
問題文全文(内容文):
<今日の単語>
1.おどろく(2)
2.ののしる(2)
3.ねんず(2)
4.おぼゆ(4)
5.しのぶ(2)
6.ながむ(1)
この動画を見る
<今日の単語>
1.おどろく(2)
2.ののしる(2)
3.ねんず(2)
4.おぼゆ(4)
5.しのぶ(2)
6.ながむ(1)
【FULL】定期テスト直前対策!ベクトル解説動画フルパック流し【数B(新課程 数C)】

単元:
#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
ベクトルのまとめ動画です。
ベクトルの基本から球面・平面の方程式まで
見たい内容のシーンをチャプターから選んで下さい!!
この動画を見る
ベクトルのまとめ動画です。
ベクトルの基本から球面・平面の方程式まで
見たい内容のシーンをチャプターから選んで下さい!!
【重大告知】数学の定期テスト対策で困っている生徒さんへ朗報

【数Ⅱ】微分法と積分法:定積分:積分を含む関数 PRIMEⅡ 531(1)

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の等式を満たす関数f(x)を求めよ。
$f(x)=6x-\int_{0}^{3}f(t)dt$
この動画を見る
次の等式を満たす関数f(x)を求めよ。
$f(x)=6x-\int_{0}^{3}f(t)dt$
Lesson9-1 NT Stage2 3rd Edition【ダスカロイがていねいに解説】

単元:
#英語(中学生)#中1英語#中2英語#形容詞・副詞#不定詞(名詞的用法・形容詞的用法・副詞的用法)
教材:
#NT ENGLISH SERIES#Third Edition Stage2#Lesson9#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. ENGLISH SERIES Third Edition Stage2 Lesson9-1のKeyPoint例文解説です。
【使用例文】
① I need a new phone because I lost my old one.
② When I took my dog for a walk, nothing strange happened.
③ Have you ever been to the restaurant on 47th Street?
④ We are looking for a restaurant to recommend to my friends.
⑤ Jane has the ability to cook Japanese and French dishes.
この動画を見る
N.T. ENGLISH SERIES Third Edition Stage2 Lesson9-1のKeyPoint例文解説です。
【使用例文】
① I need a new phone because I lost my old one.
② When I took my dog for a walk, nothing strange happened.
③ Have you ever been to the restaurant on 47th Street?
④ We are looking for a restaurant to recommend to my friends.
⑤ Jane has the ability to cook Japanese and French dishes.
Lesson9-1 ニュートレジャー Stage2 3rd Edition【ダスカロイがていねいに解説】

単元:
#英語(中学生)#中2英語#動名詞(動詞の目的語、主語・補語・前置詞の目的語、動名詞と不定詞)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage2 3rd Edition Lesson9-1のKeyPoint例文解説です。
この動画を見る
ニュートレジャー Stage2 3rd Edition Lesson9-1のKeyPoint例文解説です。
Lesson8-3 NT Stage2 3rd Edition【ダスカロイがていねいに解説】

単元:
#英語(中学生)#中2英語#人称代名詞、所有代名詞、再帰代名詞、itの特別用法、指示代名詞、不定代名詞
教材:
#NT ENGLISH SERIES#Third Edition Stage2#Lesson8#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. ENGLISH SERIES Third Edition Stage2 Lesson8-3のKeyPoint例文解説です。
【使用例文】
① Ted introduced himself to the class.
② All of the students enjoyed themselves at the welcome party.
③ I put on a new T-shirt and looked at myself in the mirror.
④ Help yourself to anything on the table.
⑤ The president himself welcomed the guests at the entrance.
⑥ The students planned the festival themselves.
⑦ We will talk with the doctor himself.
⑧ Ted is honesty itself.
この動画を見る
N.T. ENGLISH SERIES Third Edition Stage2 Lesson8-3のKeyPoint例文解説です。
【使用例文】
① Ted introduced himself to the class.
② All of the students enjoyed themselves at the welcome party.
③ I put on a new T-shirt and looked at myself in the mirror.
④ Help yourself to anything on the table.
⑤ The president himself welcomed the guests at the entrance.
⑥ The students planned the festival themselves.
⑦ We will talk with the doctor himself.
⑧ Ted is honesty itself.
Lesson8-3 ニュートレジャー Stage2 3rd Edition【ダスカロイがていねいに解説】

単元:
#英語(中学生)#中2英語#人称代名詞、所有代名詞、再帰代名詞、itの特別用法、指示代名詞、不定代名詞
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage2 3rd Edition Lesson8-3のKeyPoint例文解説です。
この動画を見る
ニュートレジャー Stage2 3rd Edition Lesson8-3のKeyPoint例文解説です。
【情報Ⅰ】フローチャートと構造

単元:
#情報Ⅰ(高校生)#プログラミング#基本的なプログラミング
指導講師:
理数個別チャンネル
問題文全文(内容文):
プログラムを作る際、下書きや設計図としてフローチャートというものを使用します。
今回は一番基本のフローチャートの読み方の解説です!
この動画を見る
プログラムを作る際、下書きや設計図としてフローチャートというものを使用します。
今回は一番基本のフローチャートの読み方の解説です!
【数Ⅱ】微分法と積分法「面積、体積」絶対値の定積分PRIMEⅡ 551

単元:
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
教材:
#PRIME数学#PRIME数学Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の定積分を求めよ。
(1) $\int_0^3 |x-1|dx$
(2) $\int_0^4 |x^2-3x|dx$
この動画を見る
次の定積分を求めよ。
(1) $\int_0^3 |x-1|dx$
(2) $\int_0^4 |x^2-3x|dx$
【数Ⅱ】式と証明:等式の証明:展開するだけの証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の等式を証明せよ。$(a-b)^3+3ab(a-b)=a^3-b^3$
この動画を見る
次の等式を証明せよ。$(a-b)^3+3ab(a-b)=a^3-b^3$
【数Ⅱ】式と証明:恒等式の証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の等式が$x$についての恒等式になるように,定数$a,b$の値を定めよ。
$\displaystyle \frac{4x+7}{(x-2)(2x+1)}=\displaystyle \frac{a}{x-2}+\displaystyle \frac{b}{2x+1}$
この動画を見る
次の等式が$x$についての恒等式になるように,定数$a,b$の値を定めよ。
$\displaystyle \frac{4x+7}{(x-2)(2x+1)}=\displaystyle \frac{a}{x-2}+\displaystyle \frac{b}{2x+1}$
【数Ⅰ】図形と計量:三角比への応用:3つのsinの比から角度を求める!

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$△ABC$において,次の等式が成り立つとき,この三角形の最も大きい角の大きさを求めよ。
$\sin A:\sin B:\sin C=7:5:3$
この動画を見る
$△ABC$において,次の等式が成り立つとき,この三角形の最も大きい角の大きさを求めよ。
$\sin A:\sin B:\sin C=7:5:3$
【数Ⅰ】図形と計量:三角比への応用:「角の二等分線」の長さの求め方!
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
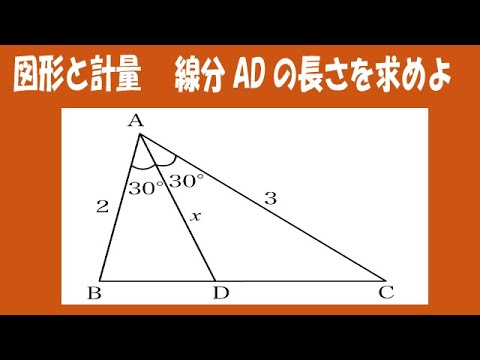
$△ABC$において,$AB=2,AC=3,A=60°$とし,$∠A$の二等分線と辺$BC$の交点を$D$とする。線分$AD$の長さを求めよ。
この動画を見る
$△ABC$において,$AB=2,AC=3,A=60°$とし,$∠A$の二等分線と辺$BC$の交点を$D$とする。線分$AD$の長さを求めよ。
Lesson11-4 NT Stage2 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(高校生)#英文法#不定詞
教材:
#NT ENGLISH SERIES#Third Edition Stage2#Lesson11#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. SERIES Third Edition Stage2 Lesson11-4の解説動画です。
不定詞の発展的用法として原型不定詞とそれを使う用法を解説しています。
主に使役動詞make, have, letとhelpの用法、少しだけ知覚動詞についても紹介をしています。
一部、to を含んだ用法として get 人 to do の用法、類似表現も紹介しています。
使えるようになるだけでなく、長文中で 気づく ことができるようになりましょう。
My mother makes me eat fresh yogurt every morning.
My brother's joke made everyone laugh.
My father sometimes lets us stay up late.
Please let me know when you need any help.
My sister had the server bring another glass of water.
How did you get him to join your project?
I helped an elderly lady (to) carry her baggage.
この動画を見る
N.T. SERIES Third Edition Stage2 Lesson11-4の解説動画です。
不定詞の発展的用法として原型不定詞とそれを使う用法を解説しています。
主に使役動詞make, have, letとhelpの用法、少しだけ知覚動詞についても紹介をしています。
一部、to を含んだ用法として get 人 to do の用法、類似表現も紹介しています。
使えるようになるだけでなく、長文中で 気づく ことができるようになりましょう。
My mother makes me eat fresh yogurt every morning.
My brother's joke made everyone laugh.
My father sometimes lets us stay up late.
Please let me know when you need any help.
My sister had the server bring another glass of water.
How did you get him to join your project?
I helped an elderly lady (to) carry her baggage.
Lesson11-4 ニュートレジャー Stage2 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中2英語#不定詞(名詞的用法・形容詞的用法・副詞的用法)#動名詞(動詞の目的語、主語・補語・前置詞の目的語、動名詞と不定詞)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage2 3rd Edition Lesson11-4の解説動画です。
不定詞の発展的用法として原型不定詞とそれを使う用法を解説しています。
主に使役動詞make, have, letとhelpの用法、少しだけ知覚動詞についても紹介をしています。
一部、to を含んだ用法として get 人 to do の用法、類似表現も紹介しています。
この動画を見る
ニュートレジャー Stage2 3rd Edition Lesson11-4の解説動画です。
不定詞の発展的用法として原型不定詞とそれを使う用法を解説しています。
主に使役動詞make, have, letとhelpの用法、少しだけ知覚動詞についても紹介をしています。
一部、to を含んだ用法として get 人 to do の用法、類似表現も紹介しています。
Lesson11-3 NT Stage2 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#英語(高校生)#英文法#中3英語#不定詞#不定詞(疑問詞+to,It~for to,ask(tell,want)O to,too~to,enough~to,not to)
教材:
#NT ENGLISH SERIES#Third Edition Stage2#Lesson11#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
Lesson11-3の文法解説動画です。
too ~toV構文、so~that SV構文、~enough to V 構文の解説とそれぞれの間違いやすいポイントについて解説をしております。
①Betty was too shy to talk to the teacher.
②She was too nervous to ask a question.
③The teacher spoke too fast for her to understand.
④The homework was too difficult for her to finish in a day.
⑤This tea is so hot that I can't drink it.
⑥The traffic was so busy that I couldn't be in time for the class.
⑦My little brother is old enough to walk to our grandparents' house.
⑧I left home early enough to be in time for school.
⑨This bag isn't big enough for me to pack all the clothes I need for travel.
この動画を見る
Lesson11-3の文法解説動画です。
too ~toV構文、so~that SV構文、~enough to V 構文の解説とそれぞれの間違いやすいポイントについて解説をしております。
①Betty was too shy to talk to the teacher.
②She was too nervous to ask a question.
③The teacher spoke too fast for her to understand.
④The homework was too difficult for her to finish in a day.
⑤This tea is so hot that I can't drink it.
⑥The traffic was so busy that I couldn't be in time for the class.
⑦My little brother is old enough to walk to our grandparents' house.
⑧I left home early enough to be in time for school.
⑨This bag isn't big enough for me to pack all the clothes I need for travel.
Lesson11-3 ニュートレジャー Stage2 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中3英語#現在完了(継続、経験、完了・結果)#不定詞(疑問詞+to,It~for to,ask(tell,want)O to,too~to,enough~to,not to)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage2 3rd Edition Lesson11-3の文法解説動画です。
too ~toV構文、so~that SV構文、~enough to V 構文の解説とそれぞれの間違いやすいポイントについて解説をしております。
この動画を見る
ニュートレジャー Stage2 3rd Edition Lesson11-3の文法解説動画です。
too ~toV構文、so~that SV構文、~enough to V 構文の解説とそれぞれの間違いやすいポイントについて解説をしております。
Lesson12-2 NT Stage2 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(中学生)#中2英語#Whで始まる疑問文、Howで始まる疑問文、付加疑問文、否定疑問文
教材:
#NT ENGLISH SERIES#Third Edition Stage2#Lesson12#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. Lesson12-1(間接疑問)の解説動画です。
間接疑問の特徴を解説します。
例文
I don't know when the party will start.
I cannot imagine what Karen wants for her birthday.
Do you know who made this birthday cake?
I wonder how many guests will come to the party.
He asked me when she would come home.
埋め込み文、主語と動詞の並び順、時制の一致、疑問詞が主語となるパターン、間接疑問が主語・補語となるもの
この動画を見る
N.T. Lesson12-1(間接疑問)の解説動画です。
間接疑問の特徴を解説します。
例文
I don't know when the party will start.
I cannot imagine what Karen wants for her birthday.
Do you know who made this birthday cake?
I wonder how many guests will come to the party.
He asked me when she would come home.
埋め込み文、主語と動詞の並び順、時制の一致、疑問詞が主語となるパターン、間接疑問が主語・補語となるもの
Lesson12-2 ニュートレジャー Stage2 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(中学生)#中2英語#Whで始まる疑問文、Howで始まる疑問文、付加疑問文、否定疑問文
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage2 3rd Edition Lesson12-2(付加疑問)の解説動画です。
付加疑問の特徴を解説します。
この動画を見る
ニュートレジャー Stage2 3rd Edition Lesson12-2(付加疑問)の解説動画です。
付加疑問の特徴を解説します。
Lesson12-1 NT Stage2 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(中学生)#英語(高校生)#英文法#中3英語#話法の転換#間接疑問文
教材:
#NT ENGLISH SERIES#Third Edition Stage2#Lesson12#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. Lesson12-1(間接疑問)の解説動画です。
間接疑問の特徴を解説します。
例文
I don't know when the party will start.
I cannot imagine what Karen wants for her birthday.
Do you know who made this birthday cake?
I wonder how many guests will come to the party.
He asked me when she would come home.
埋め込み文、主語と動詞の並び順、時制の一致、疑問詞が主語となるパターン、間接疑問が主語・補語となるもの
この動画を見る
N.T. Lesson12-1(間接疑問)の解説動画です。
間接疑問の特徴を解説します。
例文
I don't know when the party will start.
I cannot imagine what Karen wants for her birthday.
Do you know who made this birthday cake?
I wonder how many guests will come to the party.
He asked me when she would come home.
埋め込み文、主語と動詞の並び順、時制の一致、疑問詞が主語となるパターン、間接疑問が主語・補語となるもの
Lesson12-1 ニュートレジャー Stage2 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(中学生)#中3英語#間接疑問文
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage2 3rd Edition Lesson12-1(間接疑問)の解説動画です。
間接疑問の特徴を解説します。
この動画を見る
ニュートレジャー Stage2 3rd Edition Lesson12-1(間接疑問)の解説動画です。
間接疑問の特徴を解説します。
Lesson10-3 NT Stage2 3rd Edition【シュン・ヒノハラがていねいに解説】

単元:
#英語(高校生)#英文法#関係代名詞・関係副詞・複合関係詞
教材:
#NT ENGLISH SERIES#Third Edition Stage2#Lesson10#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
Lesson10-3 関係代名詞のthatを選択するケースについての解説動画です。10-2までと比べると重要度は下がりますが、その中でもテスト・入試に出されやすいケースについて詳しく解説しています。
例文
In the book, I like the boy and the dog that are traveling together.
This is the best book I have ever read.
この動画を見る
Lesson10-3 関係代名詞のthatを選択するケースについての解説動画です。10-2までと比べると重要度は下がりますが、その中でもテスト・入試に出されやすいケースについて詳しく解説しています。
例文
In the book, I like the boy and the dog that are traveling together.
This is the best book I have ever read.
Lesson10-3 ニュートレジャー Stage2 3rd Edition【シュン・ヒノハラがていねいに解説】

単元:
#英語(中学生)#中3英語#関係代名詞(主格、目的格、所有格、thatの用法、前置詞+関係代名詞)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage2 3rd Edition Lesson10-3 関係代名詞のthatを選択するケースについての解説動画です。
10-2までと比べると重要度は下がりますが、その中でもテスト・入試に出されやすいケースについて詳しく解説しています。
この動画を見る
ニュートレジャー Stage2 3rd Edition Lesson10-3 関係代名詞のthatを選択するケースについての解説動画です。
10-2までと比べると重要度は下がりますが、その中でもテスト・入試に出されやすいケースについて詳しく解説しています。
Lesson11-2 ニュートレジャー Stage2 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中3英語#不定詞(疑問詞+to,It~for to,ask(tell,want)O to,too~to,enough~to,not to)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage2 3rd Edition Lesson11-2の解説動画です。
疑問詞 to doの特徴を解説します。
この動画を見る
ニュートレジャー Stage2 3rd Edition Lesson11-2の解説動画です。
疑問詞 to doの特徴を解説します。




