鈴木貫太郎
鈴木貫太郎
 鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
どっちがでかい?大事なあの公式のエレガントな証明

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?
$999! $vs $500^{999}$
この動画を見る
どちらが大きいか?
$999! $vs $500^{999}$
ざ・見掛け倒し

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \sum_{n=1}^{10000}n^n$
$=1^1+2^2+3^3+・・・・・・9999^{9999}+10000^{10000}$を3で割った余りを求めよ.
この動画を見る
$\displaystyle \sum_{n=1}^{10000}n^n$
$=1^1+2^2+3^3+・・・・・・9999^{9999}+10000^{10000}$を3で割った余りを求めよ.
方程式
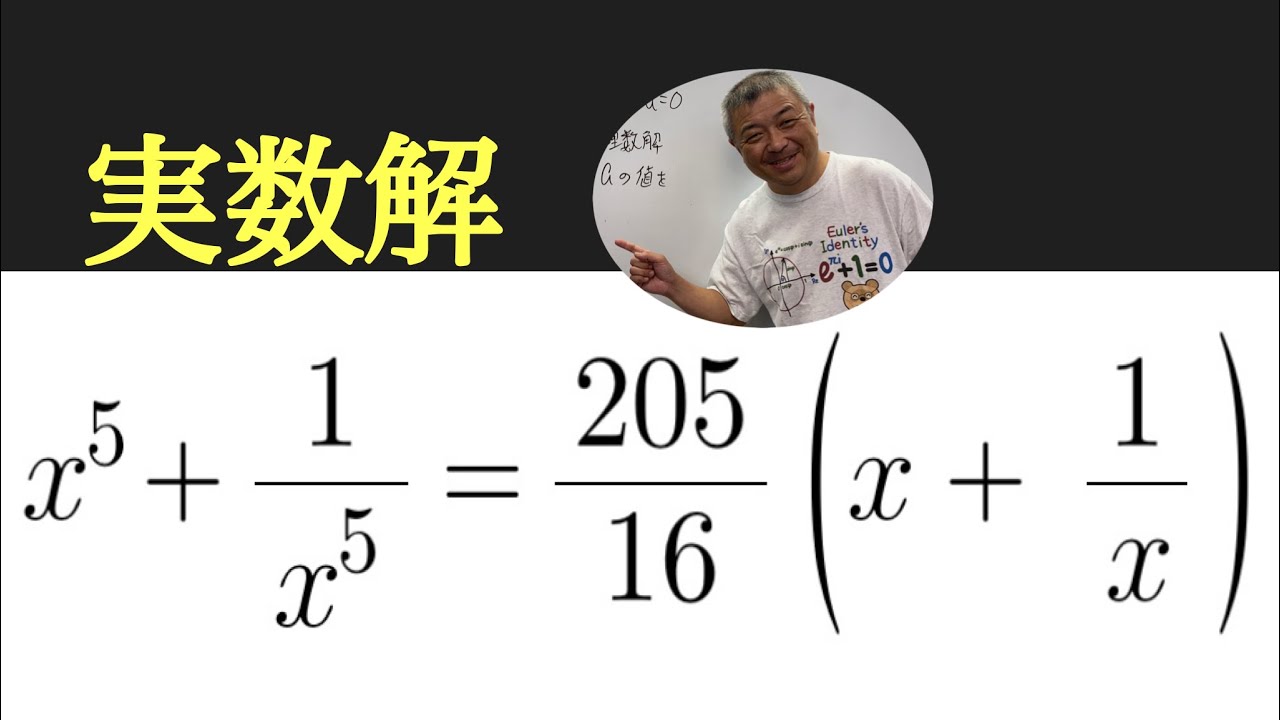
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$x^5+\dfrac{1}{x^5}=\dfrac{205}{16}\left(x+\dfrac{1}{x}\right)$
この動画を見る
実数解を求めよ.
$x^5+\dfrac{1}{x^5}=\dfrac{205}{16}\left(x+\dfrac{1}{x}\right)$
対数不等式

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
${\log_{10}(-x)}^2-\log_{10}x^2 \gt 3$
この動画を見る
これを解け.
${\log_{10}(-x)}^2-\log_{10}x^2 \gt 3$
変な指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$3^x-2^x=\sqrt{6^x}$
この動画を見る
実数解を求めよ.
$3^x-2^x=\sqrt{6^x}$
超絶良問 どっちがでかい?その差僅か0.0005

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?
$\sqrt{2022}+\sqrt{2052}$ vs $\sqrt{2032}+\sqrt{2042}$
この動画を見る
どちらが大きいか?
$\sqrt{2022}+\sqrt{2052}$ vs $\sqrt{2032}+\sqrt{2042}$
数3を使わずに分数関数の最小値を求める

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x$は正の実数である.
$\dfrac{x^2+x+196}{x+1}$は$x=\Box$のとき,最小値$\Box$となる.
$\Box$を求めよ.
この動画を見る
$x$は正の実数である.
$\dfrac{x^2+x+196}{x+1}$は$x=\Box$のとき,最小値$\Box$となる.
$\Box$を求めよ.
指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$5^{2x^2-1}-3・5^{(x+1)(x+2)}-2・5^{6(x+1)}=0$
この動画を見る
実数解を求めよ.
$5^{2x^2-1}-3・5^{(x+1)(x+2)}-2・5^{6(x+1)}=0$
比例式と整数

単元:
#数学(中学生)#中1数学#数A#比例・反比例#整数の性質#約数・倍数・整数の割り算と余り・合同式
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y,z,n$は自然数である.
$2x=3y=5z,x+y+z=n$である.
$\sqrt{xyz}$が整数となる$n$の条件を求めよ.
この動画を見る
$x,y,z,n$は自然数である.
$2x=3y=5z,x+y+z=n$である.
$\sqrt{xyz}$が整数となる$n$の条件を求めよ.
単なる計算問題

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt{99910000+\dfrac{81}{4}}$
これを解け.
この動画を見る
$\sqrt{99910000+\dfrac{81}{4}}$
これを解け.
千葉大(医)の類題 整数
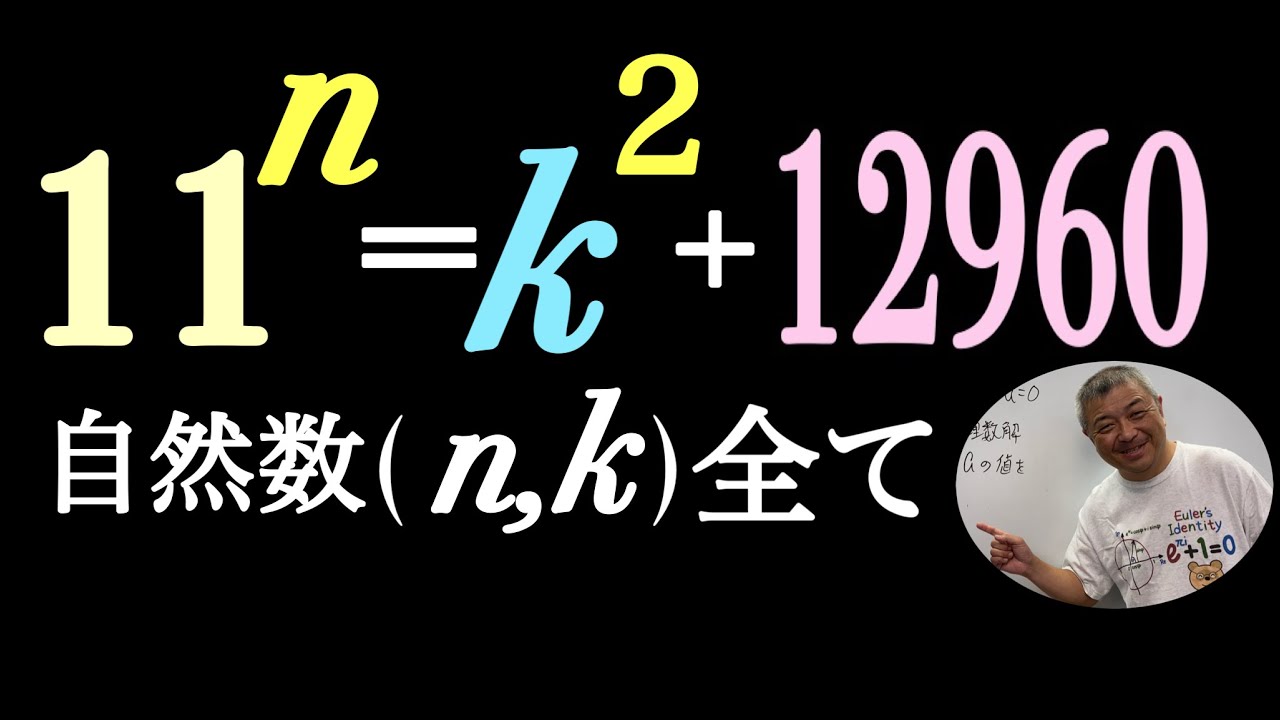
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$(n,k)$をすべて求めよ.
$11^n=k^2+12960$
千葉大(医)過去問
この動画を見る
自然数$(n,k)$をすべて求めよ.
$11^n=k^2+12960$
千葉大(医)過去問
図形 中学レベル 円の基本性質の証明
工夫して簡単に!
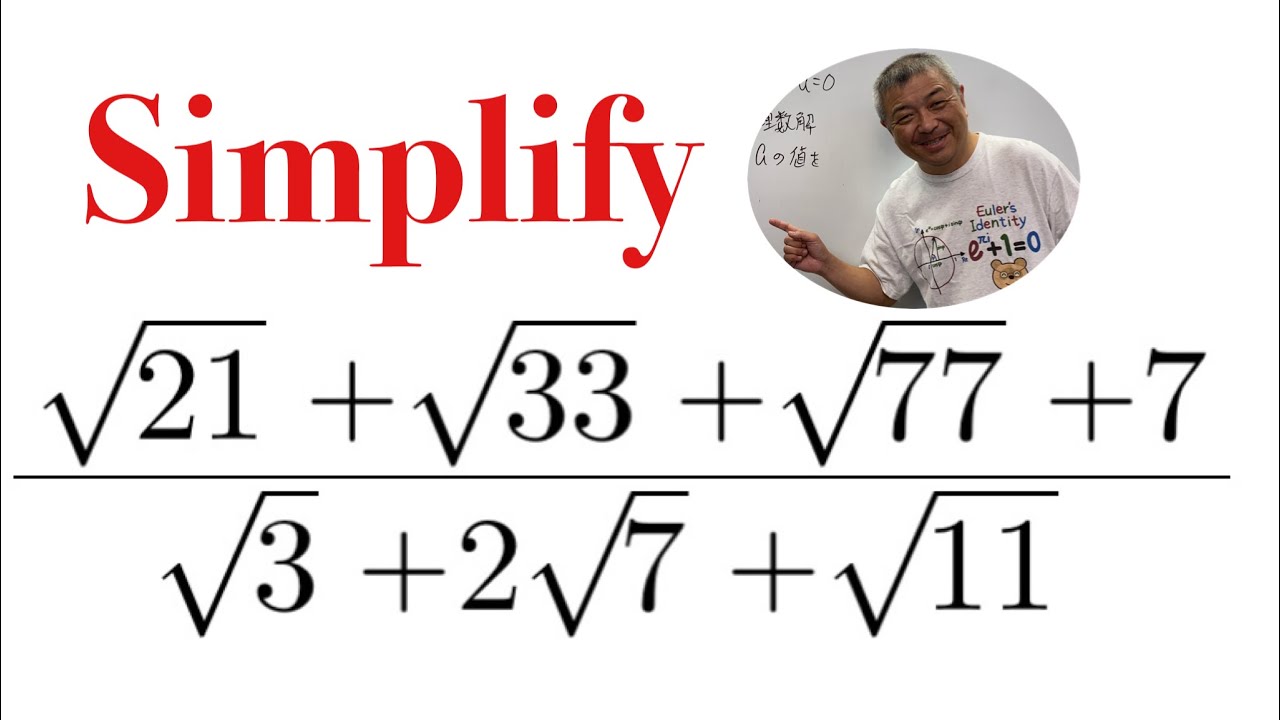
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを簡単にせよ.
$\dfrac{\sqrt{21}+\sqrt{33}+\sqrt{77}+7}{\sqrt3+2\sqrt 7+\sqrt{11}}$
この動画を見る
これを簡単にせよ.
$\dfrac{\sqrt{21}+\sqrt{33}+\sqrt{77}+7}{\sqrt3+2\sqrt 7+\sqrt{11}}$
整数問題基本

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数$m,n$をすべて求めよ.
$m^4+n^4-2mn=13$
この動画を見る
整数$m,n$をすべて求めよ.
$m^4+n^4-2mn=13$
中学レベル 倍数の見分け方の証明

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y,z$は1~9の整数である.
$XX+YY+ZZ=XYZ$
これを解け.
この動画を見る
$x,y,z$は1~9の整数である.
$XX+YY+ZZ=XYZ$
これを解け.
変な方程式 指数タワー
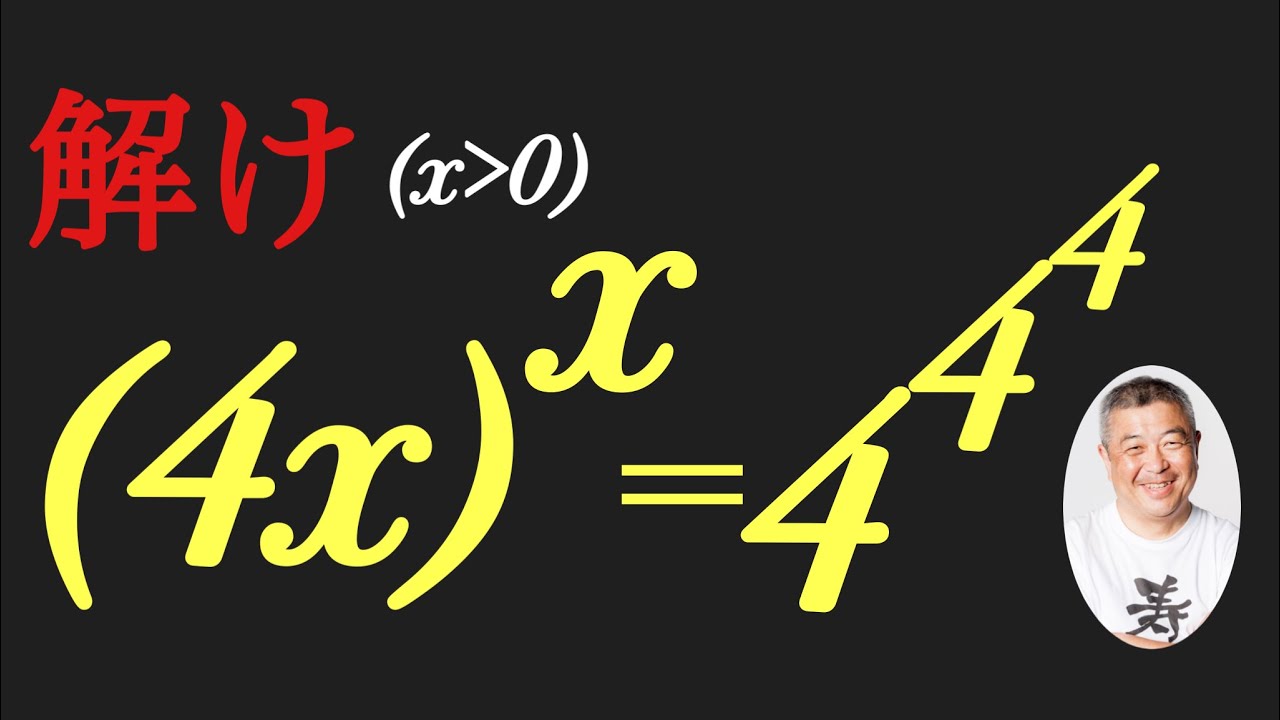
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け. $x\gt 0$
$(4x)^x=4^{4^4}$
この動画を見る
これを解け. $x\gt 0$
$(4x)^x=4^{4^4}$
変な指数方程式
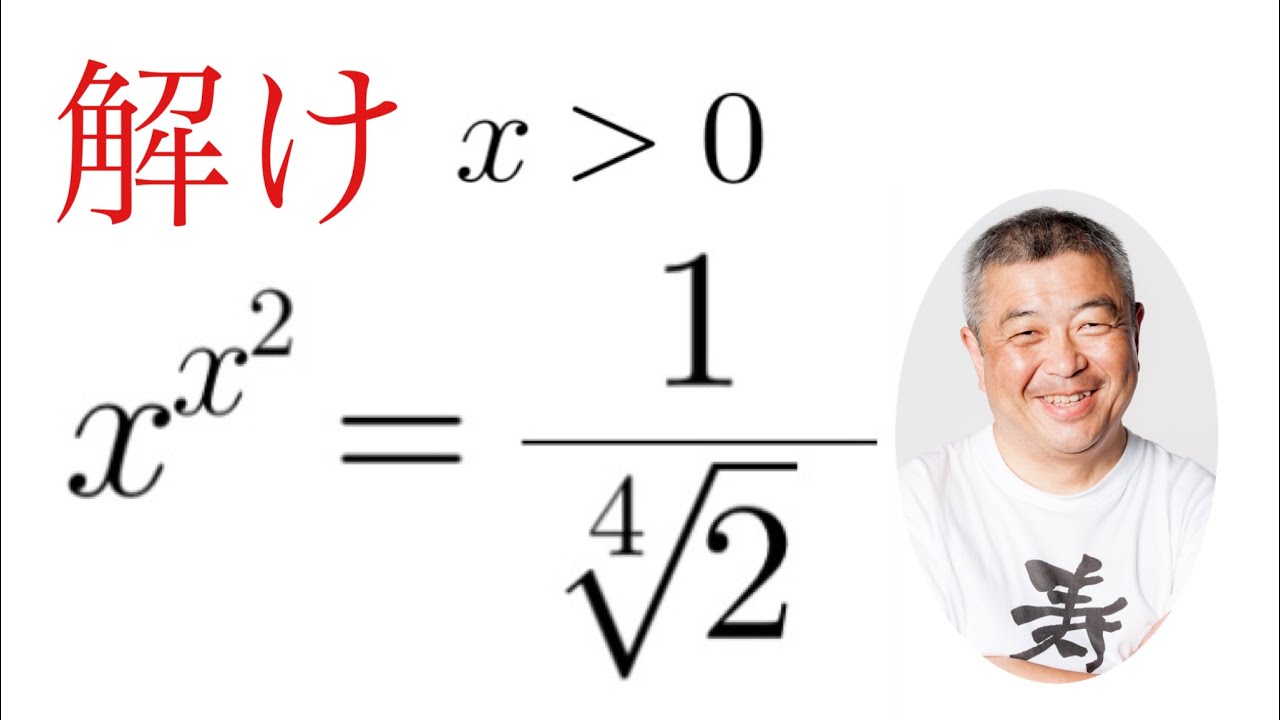
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$x\gt 0$
$x^{x^2}=\dfrac{1}{\sqrt[4]{2}}$
この動画を見る
これを解け.$x\gt 0$
$x^{x^2}=\dfrac{1}{\sqrt[4]{2}}$
2021東京海洋大 整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$P$は5以上の素数である.
$P^2-1$は$24$の倍数を示せ.
2021東京海洋大過去問
この動画を見る
$P$は5以上の素数である.
$P^2-1$は$24$の倍数を示せ.
2021東京海洋大過去問
2021一橋大(経済)補足と別解

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(sin x+1)(cos x+1)=k$の解が$0\leqq x\lt 2\pi$の範囲にちょうど2つある$k$を求めよ.
一橋大(経済)過去問
この動画を見る
$(sin x+1)(cos x+1)=k$の解が$0\leqq x\lt 2\pi$の範囲にちょうど2つある$k$を求めよ.
一橋大(経済)過去問
2021一橋(経済)後期

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(sin x+1)(cos x+1)=k$の解が$0\leqq x\lt 2\pi$の範囲にちょうど2つある$k$を求めよ.
一橋(経済)過去問
この動画を見る
$(sin x+1)(cos x+1)=k$の解が$0\leqq x\lt 2\pi$の範囲にちょうど2つある$k$を求めよ.
一橋(経済)過去問
指数方程式 答えは1つじゃないよ

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
すべての解を求めよ.
$5^x・8^{\frac{x}{x+1}}=100$
この動画を見る
すべての解を求めよ.
$5^x・8^{\frac{x}{x+1}}=100$
失敗しないたすきがけ因数分解

三角関数基本

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
値を求めよ.
$\cos \dfrac{\pi}{7}・\cos \dfrac{2\pi}{7}・\cos\dfrac{3\pi}{7}$
この動画を見る
値を求めよ.
$\cos \dfrac{\pi}{7}・\cos \dfrac{2\pi}{7}・\cos\dfrac{3\pi}{7}$
方程式
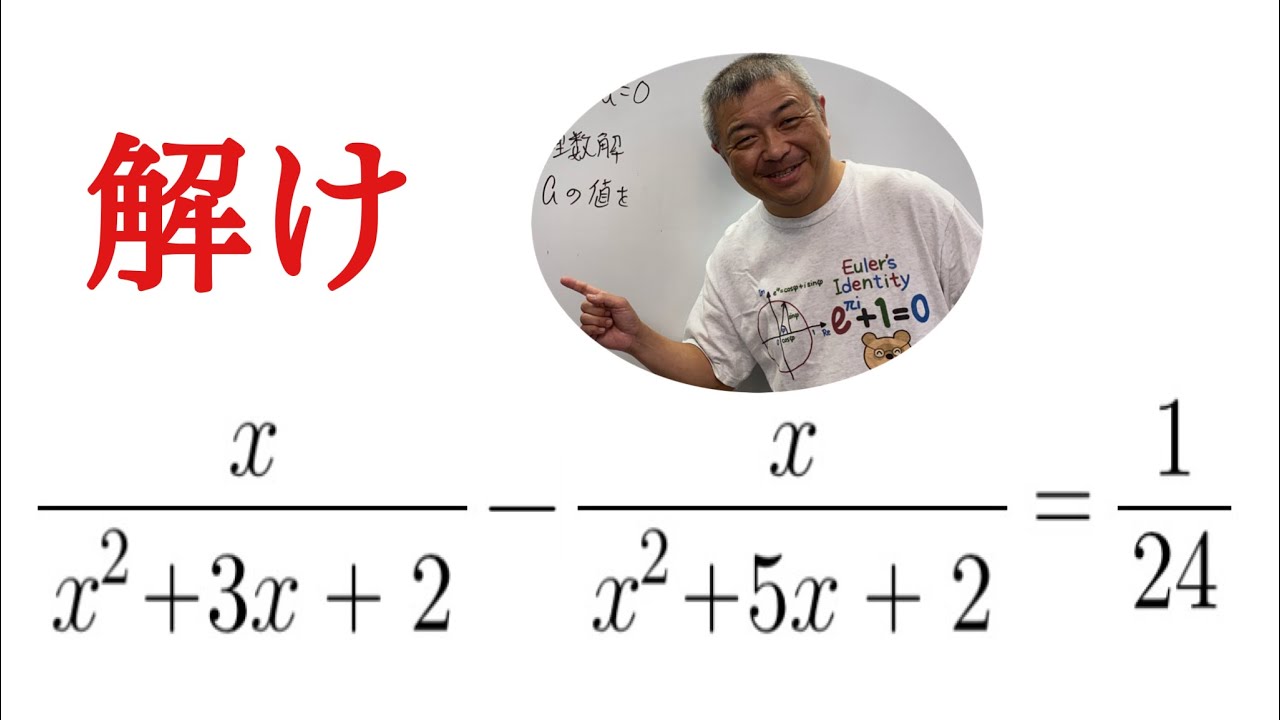
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\dfrac{x}{x^2+3x+2}-\dfrac{x}{x^2+5x+2}=\dfrac{1}{24}$
この動画を見る
これを解け.
$\dfrac{x}{x^2+3x+2}-\dfrac{x}{x^2+5x+2}=\dfrac{1}{24}$
算数

未知数2で式1つの方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これの実数解を求めよ.
$x^2+y^2+15=\sqrt 6(x-3y)$
この動画を見る
これの実数解を求めよ.
$x^2+y^2+15=\sqrt 6(x-3y)$
4乗根の方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$\sqrt[4]{97-x}+\sqrt[4]{x-15}=4$
この動画を見る
実数解を求めよ.
$\sqrt[4]{97-x}+\sqrt[4]{x-15}=4$
虚数係数の二次方程式(類)横浜市立(医)

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$iz^2-4iz+3i+\sqrt3=0$
横浜市立(医)過去問
この動画を見る
これを解け.
$iz^2-4iz+3i+\sqrt3=0$
横浜市立(医)過去問
2022年問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(45+\sqrt{2022})^{2022}$の1の位を求めよ.
この動画を見る
$(45+\sqrt{2022})^{2022}$の1の位を求めよ.
中学レベル 図形問題