 鈴木貫太郎
鈴木貫太郎
 鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
場合の数

単元:
#数A#場合の数と確率#整数の性質#場合の数#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n,x,y,z$は$0$以上の整数
$2x+y+z=n$を満たす$(x,y,z)$は何組あるか求めよ
この動画を見る
$n,x,y,z$は$0$以上の整数
$2x+y+z=n$を満たす$(x,y,z)$は何組あるか求めよ
場合の数

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n,x,y,z$は0以上の整数である.
$2x+y+z=n$を満たす$(x,y,z)$は何組あるか.
この動画を見る
$n,x,y,z$は0以上の整数である.
$2x+y+z=n$を満たす$(x,y,z)$は何組あるか.
整数問題 二項定理

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2^{3^n}+1$は3で何回割り切れるか求めよ。$(n$自然数$)$
この動画を見る
$2^{3^n}+1$は3で何回割り切れるか求めよ。$(n$自然数$)$
大阪市立大 確率

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$A,B$が連続対戦(引分無し)
$A$が勝つ確率は毎回$P$
$A$が$B$より先に2連勝する確率を求めよ
大阪市立大過去問
この動画を見る
$A,B$が連続対戦(引分無し)
$A$が勝つ確率は毎回$P$
$A$が$B$より先に2連勝する確率を求めよ
大阪市立大過去問
慶応義塾大 4次方程式

単元:
#関数と極限#微分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3x^4-4x^3-12x^2-k=0$が相異なる4つの実数解をもつ$k$の範囲
そのときの4つの解のうち最大のものを$\alpha$とする。
$\alpha$の範囲を求めよ
出典:1989年慶應義塾大学 過去問
この動画を見る
$3x^4-4x^3-12x^2-k=0$が相異なる4つの実数解をもつ$k$の範囲
そのときの4つの解のうち最大のものを$\alpha$とする。
$\alpha$の範囲を求めよ
出典:1989年慶應義塾大学 過去問
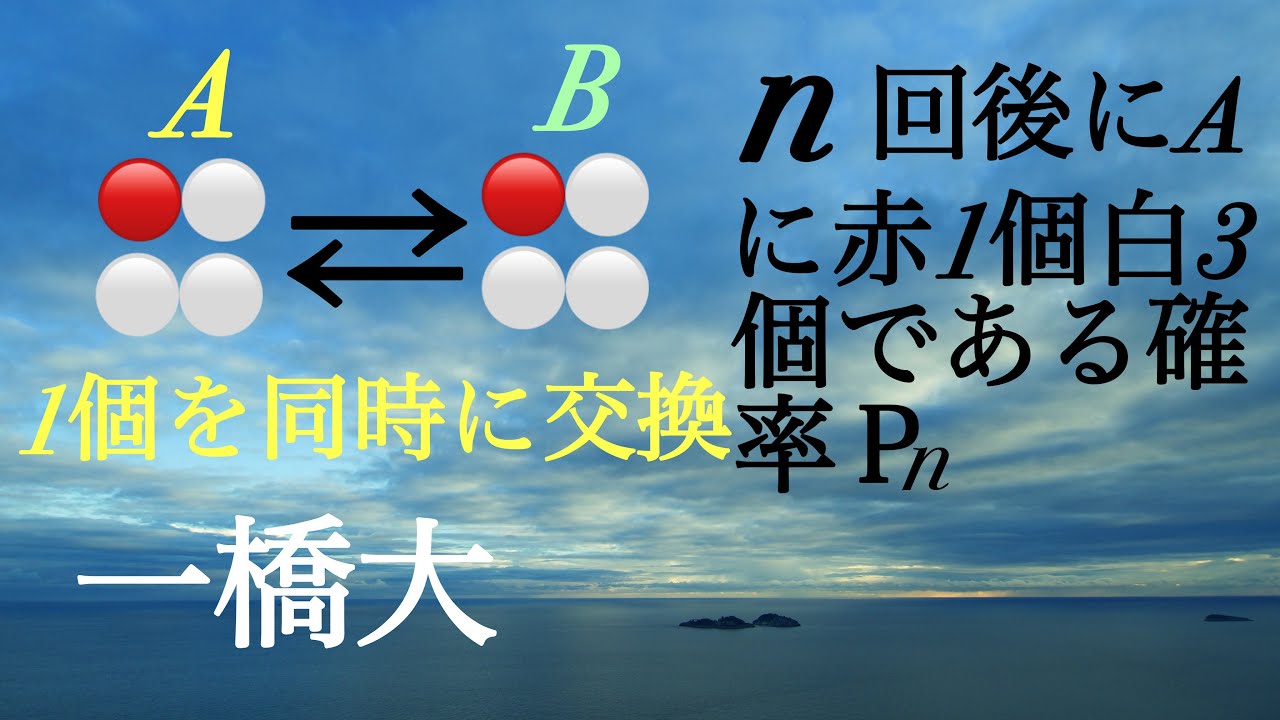
一橋大 確率漸化式
単元:
#数A#場合の数と確率#確率#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
動画内の図のように同時に玉を1個入れ替える
$n$回目に$A$に赤1個、白3個となっている確率$P_n$を求めよ
出典:一橋大学 過去問
この動画を見る
動画内の図のように同時に玉を1個入れ替える
$n$回目に$A$に赤1個、白3個となっている確率$P_n$を求めよ
出典:一橋大学 過去問
名古屋市立大 3次方程式が相違3実数解を持つ条件

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋市立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3-kx+k=0$が相異なる3つの実数解をもつ$k$の範囲を求めよ
出典:名古屋市立大学 過去問
この動画を見る
$x^3-kx+k=0$が相異なる3つの実数解をもつ$k$の範囲を求めよ
出典:名古屋市立大学 過去問
一橋大 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$p,q$自然数
$3p^3-p^2q-pq^2+3q^3=2013$を満たす$(p,q)$すべて求めよ
出典:一橋大学 過去問
この動画を見る
$p,q$自然数
$3p^3-p^2q-pq^2+3q^3=2013$を満たす$(p,q)$すべて求めよ
出典:一橋大学 過去問
東邦(医)三角関数 最大値

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#数学(高校生)#東邦大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2\sin x\cos x+3\sqrt{ 2 }(\cos x+\sin x)$の最大値を求めよ
出典:東邦大学医学部 過去問
この動画を見る
$2\sin x\cos x+3\sqrt{ 2 }(\cos x+\sin x)$の最大値を求めよ
出典:東邦大学医学部 過去問
2020年東大 ヨビノりたくみさん解説

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a \gt 0,b \gt 0$
$C:y=x^3-3ax^2+b$
条件1 $C$は$x$軸に接する
条件2 $x$軸と$C$で囲まれた領域(除く境界)に格子点1つのみ
$b$を$a$で表せ
$a$の範囲を求めよ
出典:2020年東京大学 過去問
この動画を見る
$a \gt 0,b \gt 0$
$C:y=x^3-3ax^2+b$
条件1 $C$は$x$軸に接する
条件2 $x$軸と$C$で囲まれた領域(除く境界)に格子点1つのみ
$b$を$a$で表せ
$a$の範囲を求めよ
出典:2020年東京大学 過去問
もっちゃんと数学 球の体積はなぜ(4πr^3)÷3なの?中学範囲で

単元:
#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師:
鈴木貫太郎
問題文全文(内容文):
球の体積はなぜ$\displaystyle \frac{4}{3}\pi r^3$なのか。
解説動画です
この動画を見る
球の体積はなぜ$\displaystyle \frac{4}{3}\pi r^3$なのか。
解説動画です
東京薬科大 数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$1,11,111,1111,…$
第$n$項と初項から第$n$項までの和を求めよ
出典:東京薬科大学 過去問
この動画を見る
$1,11,111,1111,…$
第$n$項と初項から第$n$項までの和を求めよ
出典:東京薬科大学 過去問
嵐の方程式 5-1=0 をオイラーの公式を使って よさまつが証明するよ

単元:
#数A#数Ⅱ#図形の性質#式と証明#恒等式・等式・不等式の証明#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
オイラーの公式 説明動画です
この動画を見る
オイラーの公式 説明動画です
慶応義塾大 極限値
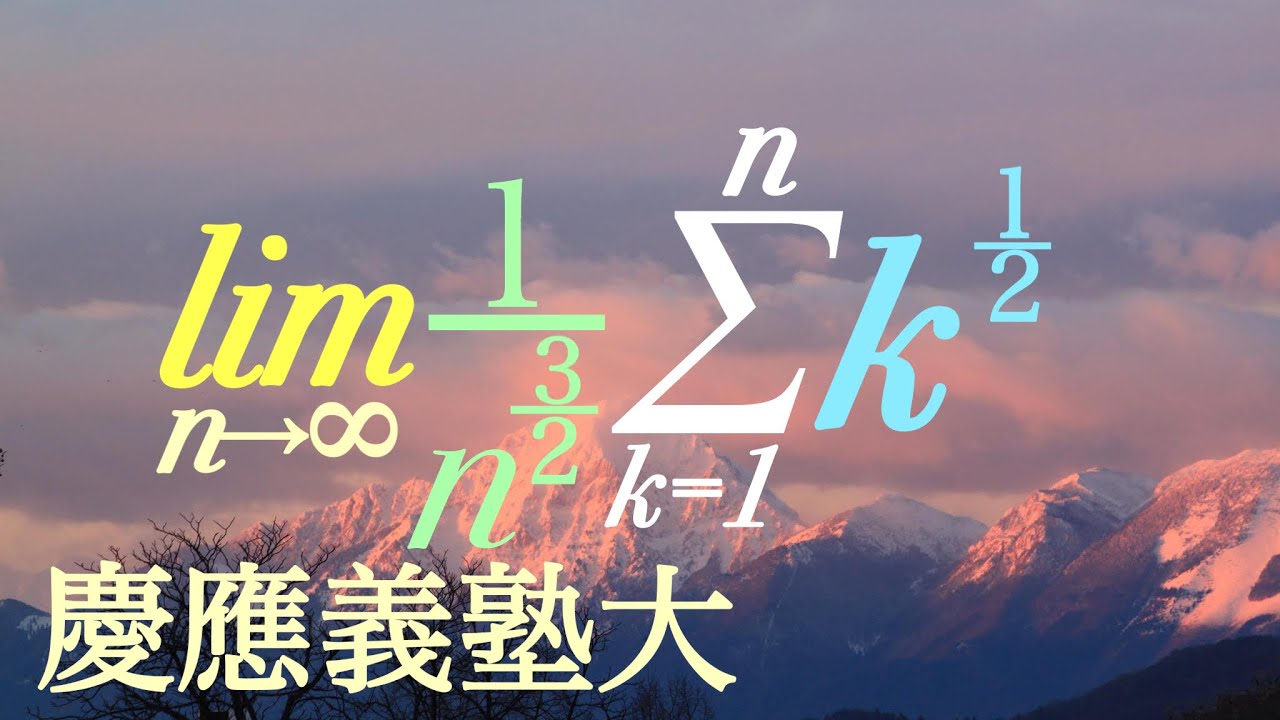
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n^{\displaystyle \frac{3}{2}}}\displaystyle \sum_{k=1}^n k^{\displaystyle \frac{1}{2}}$
出典:慶應義塾大学 過去問
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n^{\displaystyle \frac{3}{2}}}\displaystyle \sum_{k=1}^n k^{\displaystyle \frac{1}{2}}$
出典:慶應義塾大学 過去問
順天堂大(医)等比数列の和の収束

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#数B#順天堂大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
{$a_n$}は等比数列
無限級数
$a_2+a_4+a_6+…$は$\displaystyle \frac{12}{5}$に収束
$a_3+a_6+a_9+…$は$\displaystyle \frac{24}{19}$に収束
{$a_n$}の公比、初項、無限階数$a_1+a_2+1_3+…$は[ ]に収束するか求めよ
出典:順天堂大学医学部 過去問
この動画を見る
{$a_n$}は等比数列
無限級数
$a_2+a_4+a_6+…$は$\displaystyle \frac{12}{5}$に収束
$a_3+a_6+a_9+…$は$\displaystyle \frac{24}{19}$に収束
{$a_n$}の公比、初項、無限階数$a_1+a_2+1_3+…$は[ ]に収束するか求めよ
出典:順天堂大学医学部 過去問
2020年 大阪大 確率漸化式

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$Q$は$A$にいる。
サイコロを振って
$1$→時計回りに隣へ
$2$→反時計回りに隣へ
$3~6$→動かない
$n$回目に$A$にいる確率を$P_n$
(1)
$P_2$を求めよ
(2)
$P_{n+1}$を$P_n$で表せ
(3)
$P_n$を求めよ
出典:2020年大阪大学 過去問
この動画を見る
$Q$は$A$にいる。
サイコロを振って
$1$→時計回りに隣へ
$2$→反時計回りに隣へ
$3~6$→動かない
$n$回目に$A$にいる確率を$P_n$
(1)
$P_2$を求めよ
(2)
$P_{n+1}$を$P_n$で表せ
(3)
$P_n$を求めよ
出典:2020年大阪大学 過去問
山梨大 複素数の4乗根

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#山梨大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z$複素数
$z^4=-8-8\sqrt{ 3 }i$
出典:山梨大学 過去問
この動画を見る
$z$複素数
$z^4=-8-8\sqrt{ 3 }i$
出典:山梨大学 過去問
東京医科大 極限値

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_n=7n^2+n(n$自然数$)$
$\displaystyle \lim_{ n \to \infty } log(\displaystyle \frac{a_{n+1}-6}{a_n})^{9n}$
出典:東京医科大学 過去問
この動画を見る
$a_n=7n^2+n(n$自然数$)$
$\displaystyle \lim_{ n \to \infty } log(\displaystyle \frac{a_{n+1}-6}{a_n})^{9n}$
出典:東京医科大学 過去問
杏林大(医)極限値

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sqrt{ \cos5x }-\sqrt{ \cos3x }}{x^2}$
出典:杏林大学医学部 過去問
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sqrt{ \cos5x }-\sqrt{ \cos3x }}{x^2}$
出典:杏林大学医学部 過去問
福井大 積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#福井大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^3-3x^2+ax+b$
$f(3)=f'(3)=0$
$f(x)$と$x$軸とで囲まれた面積を求めよ
出典:2000年福井大学 過去問
この動画を見る
$f(x)=x^3-3x^2+ax+b$
$f(3)=f'(3)=0$
$f(x)$と$x$軸とで囲まれた面積を求めよ
出典:2000年福井大学 過去問
指数方程式 指数公式 杏林大

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$4^x-1=2^{x-\displaystyle \frac{1}{2}}$
出典:杏林大学 過去問
この動画を見る
$4^x-1=2^{x-\displaystyle \frac{1}{2}}$
出典:杏林大学 過去問
福井大 2次方程式と複素平面

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#複素数平面#2次方程式と2次不等式#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#福井大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(k \gt 0)$
$x^2-2kx+2k^2=0$の解のうち虚部が正の方を$\alpha$
複素平面上で$0,\alpha,\alpha^2$が二等辺三角形になる。
$k$の値を求めよ
出典:2000年福井大学 過去問
この動画を見る
$(k \gt 0)$
$x^2-2kx+2k^2=0$の解のうち虚部が正の方を$\alpha$
複素平面上で$0,\alpha,\alpha^2$が二等辺三角形になる。
$k$の値を求めよ
出典:2000年福井大学 過去問
お茶の水女子大 多項式の展開

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)#お茶の水女子大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(1+x+x^2+x^3+…+x^m)^n$
$0 \leqq k \leqq m$ $n \geqq 1$
$x^k$の係数を求めよ
出典:2000年お茶の水女子大学 過去問
この動画を見る
$(1+x+x^2+x^3+…+x^m)^n$
$0 \leqq k \leqq m$ $n \geqq 1$
$x^k$の係数を求めよ
出典:2000年お茶の水女子大学 過去問
九州大 三次方程式と無理数

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#複素数と方程式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z=\cos2 0^{ \circ }+i \sin20^{ \circ }$
$\alpha=z+\bar{ z }$
(1)
$\alpha$を解に持つ整数、係数の3次方程式を求めよ
(2)
(1)で求めた方程式は相異なる3つの実数解をもち、それらはすべて無理数となることを示せ
(3)
$\alpha$を解にもつ有理数係数の2次方程式はないことを示せ
出典:2000年九州大学 過去問
この動画を見る
$z=\cos2 0^{ \circ }+i \sin20^{ \circ }$
$\alpha=z+\bar{ z }$
(1)
$\alpha$を解に持つ整数、係数の3次方程式を求めよ
(2)
(1)で求めた方程式は相異なる3つの実数解をもち、それらはすべて無理数となることを示せ
(3)
$\alpha$を解にもつ有理数係数の2次方程式はないことを示せ
出典:2000年九州大学 過去問
横浜国大 三角方程式 4倍角

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$0 \leqq \theta \lt 2\pi$
$1-2\cos 3\theta+\cos4\theta=0$
解の個数を求めよ
出典:2000年横浜国立大学 過去問
この動画を見る
$0 \leqq \theta \lt 2\pi$
$1-2\cos 3\theta+\cos4\theta=0$
解の個数を求めよ
出典:2000年横浜国立大学 過去問
山梨大 2次方程式と複素数平面

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#複素数平面#2次方程式と2次不等式#複素数平面#学校別大学入試過去問解説(数学)#山梨大学#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2-2kx+k=0$は実数解なし
2つの解$\alpha,\beta$と1を複素中面で結ぶと正三角形となる。
$k$の値を求めよ
出典:2000年山梨大学 過去問
この動画を見る
$x^2-2kx+k=0$は実数解なし
2つの解$\alpha,\beta$と1を複素中面で結ぶと正三角形となる。
$k$の値を求めよ
出典:2000年山梨大学 過去問
麻布獣医 整数 素数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$P$素数、$a,b$自然数
$P=a^3+2a^2b-2ab^2-b^3$
$P$の1の位の数を求めよ
出典:麻布大学獣医学部 過去問
この動画を見る
$P$素数、$a,b$自然数
$P=a^3+2a^2b-2ab^2-b^3$
$P$の1の位の数を求めよ
出典:麻布大学獣医学部 過去問
学習院大 整式の剰余 積の微分公式証明

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#学習院大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^n-1$を$(x-1)^2$で割った余りを求めよ
出典:学習院大学 過去問
この動画を見る
$x^n-1$を$(x-1)^2$で割った余りを求めよ
出典:学習院大学 過去問
甲南大 関数の最小値

単元:
#大学入試過去問(数学)#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#甲南大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=(x^2-x+a)^2-x^2+x$の最小値を求めよ
出典:甲南大学 過去問
この動画を見る
$f(x)=(x^2-x+a)^2-x^2+x$の最小値を求めよ
出典:甲南大学 過去問
九州大 COS7.5° 複素数
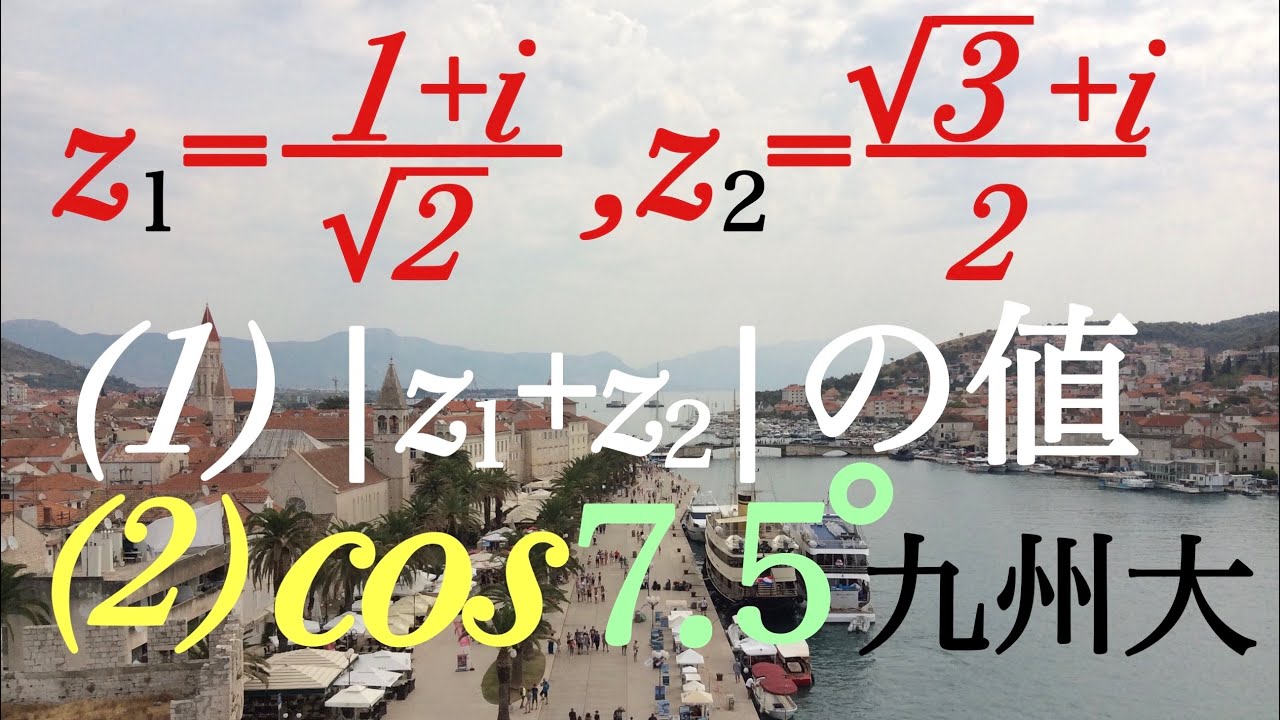
単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z_1=\displaystyle \frac{1+i}{\sqrt{ 2 }},z_2=\displaystyle \frac{\sqrt{ 3 }+i}{2}$
(1)
$|z_1+z_2|$の値を求めよ
(2)
$\cos 7.5^{ \circ }$を求めよ
出典:1972年九州大学 過去問
この動画を見る
$z_1=\displaystyle \frac{1+i}{\sqrt{ 2 }},z_2=\displaystyle \frac{\sqrt{ 3 }+i}{2}$
(1)
$|z_1+z_2|$の値を求めよ
(2)
$\cos 7.5^{ \circ }$を求めよ
出典:1972年九州大学 過去問



