文章題
文章題
2024年栄東中（A）算数大問①（１）～（４）中学受験指導歴２０年以上のプロ解説
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#規則性（周期算・方陣算・数列・日暦算・N進法）#文章題#売買損益と食塩水#栄東中学
指導講師：
重吉
問題文全文(内容文)：
次の▭に入る数を答えなさい。
(1) $(2\dfrac{1}{2}-1.75)\times3.4\div\{ (1\dfrac{1}{4}-\dfrac{1}{5})\times\dfrac{5}{7} \}+\dfrac{3}{5}=\Box$
(2) $202.4\div(50-\Box\div\dfrac{2}{81})+1.2=10$
(3) $\dfrac{1}{2\times3}=\dfrac{1}{2}-\dfrac{1}{3}$, $\dfrac{1}{3\times4}=\dfrac{1}{3}-\dfrac{1}{4}$, ………を利用すると、
$\dfrac{\Box}{440\times441}+\dfrac{\Box}{441\times442}+\cdots+\dfrac{\Box}{458\times459}+\dfrac{\Box}{459\times460}=\dfrac{1}{2024}$
ただし、▭にはすべて同じ数が入ります。
(4)いくらかの量の10 %の食塩水に8 %の食塩水200 gを入れてよく混ぜて9.2 %にする予定でしたが、8 %の食塩水▭gを入れたため8.4 %になりました。
この動画を見る
次の▭に入る数を答えなさい。
(1) $(2\dfrac{1}{2}-1.75)\times3.4\div\{ (1\dfrac{1}{4}-\dfrac{1}{5})\times\dfrac{5}{7} \}+\dfrac{3}{5}=\Box$
(2) $202.4\div(50-\Box\div\dfrac{2}{81})+1.2=10$
(3) $\dfrac{1}{2\times3}=\dfrac{1}{2}-\dfrac{1}{3}$, $\dfrac{1}{3\times4}=\dfrac{1}{3}-\dfrac{1}{4}$, ………を利用すると、
$\dfrac{\Box}{440\times441}+\dfrac{\Box}{441\times442}+\cdots+\dfrac{\Box}{458\times459}+\dfrac{\Box}{459\times460}=\dfrac{1}{2024}$
ただし、▭にはすべて同じ数が入ります。
(4)いくらかの量の10 %の食塩水に8 %の食塩水200 gを入れてよく混ぜて9.2 %にする予定でしたが、8 %の食塩水▭gを入れたため8.4 %になりました。
2024年栄東中（A）算数大問①（１）～（４）中学受験指導歴２０年以上のプロ解説
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#文章題#売買損益と食塩水#栄東中学
指導講師：
重吉
問題文全文(内容文)：
（１）
$(2\dfrac{1}{2}-1.75)\times3.4\div\{ (1\dfrac{1}{4}-\dfrac{1}{5})\times\dfrac{5}{7} \}+\dfrac{3}{5}=\Box$
（２）
$202.4\div(50-\Box\div\dfrac{2}{81})+1.2=10$
（３）
$\dfrac{1}{2\times3}=\dfrac{1}{2}-\dfrac{1}{3}$
$\dfrac{1}{3\times4}=\dfrac{1}{3}-\dfrac{1}{4}$
を利用すると、
$\dfrac{\Box}{440\times441}+\dfrac{\Box}{441\times442}+\cdots+\dfrac{\Box}{458\times459}+\dfrac{\Box}{459\times460}=\dfrac{1}{2024}$
ただし、▭にはすべて同じ数が入ります。
（４）
いくらの量の10 %の食塩水に8 %の食塩水200 gを入れてよく混ぜて9.2 %にする予定でしたが、8 %の食塩水▭gをいれたため8.4 %になりました。
この動画を見る
（１）
$(2\dfrac{1}{2}-1.75)\times3.4\div\{ (1\dfrac{1}{4}-\dfrac{1}{5})\times\dfrac{5}{7} \}+\dfrac{3}{5}=\Box$
（２）
$202.4\div(50-\Box\div\dfrac{2}{81})+1.2=10$
（３）
$\dfrac{1}{2\times3}=\dfrac{1}{2}-\dfrac{1}{3}$
$\dfrac{1}{3\times4}=\dfrac{1}{3}-\dfrac{1}{4}$
を利用すると、
$\dfrac{\Box}{440\times441}+\dfrac{\Box}{441\times442}+\cdots+\dfrac{\Box}{458\times459}+\dfrac{\Box}{459\times460}=\dfrac{1}{2024}$
ただし、▭にはすべて同じ数が入ります。
（４）
いくらの量の10 %の食塩水に8 %の食塩水200 gを入れてよく混ぜて9.2 %にする予定でしたが、8 %の食塩水▭gをいれたため8.4 %になりました。
2024年聖光学院中算数大問①（１）～（３）中学受験指導歴２０年以上のプロ解説
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#過去問解説(学校別)#文章題#仕事算とニュートン算#聖光学院中学
指導講師：
重吉
問題文全文(内容文)：
（１）
次の計算の▭に当てはまる数を答えなさい。
$3\div\{ (\Box+\dfrac{1}{3})\times\dfrac{9}{11} \}-1.375=1\dfrac{5}{6}$
（２）
1から120までの整数のうち、3でも5でも割り切れない数の総和を求めなさい。
（３）
ある仕事を終わらせるのにAさんだけでは60日、Bさんだけでは50日、Cさんだけでは40日かかります。
この仕事を、一日目はAさんとBさんが行い、二日目はBさんとCさんが行い、三日目はCさんとAさんが行い、四日目はまたAさんとBさんというように、三日周期で行うと、始めてから何日目に終わりますか。
この動画を見る
（１）
次の計算の▭に当てはまる数を答えなさい。
$3\div\{ (\Box+\dfrac{1}{3})\times\dfrac{9}{11} \}-1.375=1\dfrac{5}{6}$
（２）
1から120までの整数のうち、3でも5でも割り切れない数の総和を求めなさい。
（３）
ある仕事を終わらせるのにAさんだけでは60日、Bさんだけでは50日、Cさんだけでは40日かかります。
この仕事を、一日目はAさんとBさんが行い、二日目はBさんとCさんが行い、三日目はCさんとAさんが行い、四日目はまたAさんとBさんというように、三日周期で行うと、始めてから何日目に終わりますか。
2024年聖光学院中算数大問①（１）～（３）中学受験指導歴２０年以上のプロ解説
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#過去問解説(学校別)#文章題#仕事算とニュートン算#聖光学院中学
指導講師：
重吉
問題文全文(内容文)：
(1)次の計算の▭に当てはまる数を答えなさい。
$3\div\{ (\Box+\dfrac{1}{3})\times\dfrac{9}{11} \}-1.375=1\dfrac{5}{6}$
(2) 1から120までの整数のうち、3でも5でも割り切れない数の総和を求めなさい。
(3) ある仕事を終わらせるのにAさんだけでは60日、Bさんだけでは50日、Cさんだけでは40日かかります。
この仕事を、1日目はAさんとBさんが行い、2日目はBさんとCさんが行い、3日目はCさんとAさんが行い、4日目はまたAさんとBさんというように、3日周期で行うと、始めてから何日目に終わりますか。
この動画を見る
(1)次の計算の▭に当てはまる数を答えなさい。
$3\div\{ (\Box+\dfrac{1}{3})\times\dfrac{9}{11} \}-1.375=1\dfrac{5}{6}$
(2) 1から120までの整数のうち、3でも5でも割り切れない数の総和を求めなさい。
(3) ある仕事を終わらせるのにAさんだけでは60日、Bさんだけでは50日、Cさんだけでは40日かかります。
この仕事を、1日目はAさんとBさんが行い、2日目はBさんとCさんが行い、3日目はCさんとAさんが行い、4日目はまたAさんとBさんというように、3日周期で行うと、始めてから何日目に終わりますか。
2024年市川中算数大問①（１）～（５）中学受験指導歴２０年以上のプロ解説
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#文章題#売買損益と食塩水#平面図形#角度と面積#場合の数#場合の数#推理と論証#推理と論証#市川中学
指導講師：
重吉
問題文全文(内容文)：
※図は動画内参照
(1)
$2-(\dfrac{7}{2} \times 0.8-1) \div 6+\dfrac{4}{15}-\dfrac{1}{20}$
(2)
4 %の食塩水110 gに食塩を10 g加えてよくかきまぜたあと、できた食塩水を10 g捨てます。その後、水を何gか加えてよくかきまぜたところ、4 %の食塩水ができました。このとき、水を何g加えたか求めなさい。
(3)
1組から4組まである学校に通っているA,B,C,Dの四人が次のように話しています。このとき、Aの今年の組を答えなさい。ただし、昨年、今年ともに、A,B,C,Dの4人のうち、どの2人も同じ組にはいないものとします。
A「4人中3人は昨年と今年で違う組になったね」
B「僕は昨年も今年も偶数組だった」
C「私は昨年も今年も同じ組だったわ」
D「私は昨年4組だった」
(4)
次の図のような、一列目と二列目は二人がけ、三列目は三人がけの七人乗りの車に、大人三人、子ども四人が乗るときの座り方を考えます。運転席には大人が座り、各列とも子供が座る隣に最低一人が座るとき、座り方は何通りあるか答えなさい。
(5)
次の図は半径2 cmの円で、円周上の点は円周を12等分する点です。1辺が1 cmの正方形をA、1辺が1 cmの正三角形をBとするとき、灰色部分の面積は、Aが$\boxed{ア }$枚分の面積とBが$\boxed{イ }$枚分の面積の合計になります。$\boxed{ア }$と$\boxed{イ }$に当てはまる数を答えなさい。
この動画を見る
※図は動画内参照
(1)
$2-(\dfrac{7}{2} \times 0.8-1) \div 6+\dfrac{4}{15}-\dfrac{1}{20}$
(2)
4 %の食塩水110 gに食塩を10 g加えてよくかきまぜたあと、できた食塩水を10 g捨てます。その後、水を何gか加えてよくかきまぜたところ、4 %の食塩水ができました。このとき、水を何g加えたか求めなさい。
(3)
1組から4組まである学校に通っているA,B,C,Dの四人が次のように話しています。このとき、Aの今年の組を答えなさい。ただし、昨年、今年ともに、A,B,C,Dの4人のうち、どの2人も同じ組にはいないものとします。
A「4人中3人は昨年と今年で違う組になったね」
B「僕は昨年も今年も偶数組だった」
C「私は昨年も今年も同じ組だったわ」
D「私は昨年4組だった」
(4)
次の図のような、一列目と二列目は二人がけ、三列目は三人がけの七人乗りの車に、大人三人、子ども四人が乗るときの座り方を考えます。運転席には大人が座り、各列とも子供が座る隣に最低一人が座るとき、座り方は何通りあるか答えなさい。
(5)
次の図は半径2 cmの円で、円周上の点は円周を12等分する点です。1辺が1 cmの正方形をA、1辺が1 cmの正三角形をBとするとき、灰色部分の面積は、Aが$\boxed{ア }$枚分の面積とBが$\boxed{イ }$枚分の面積の合計になります。$\boxed{ア }$と$\boxed{イ }$に当てはまる数を答えなさい。
2024年東洋英和女学院中算数大問①（１）～（４）中学受験指導歴２０年以上のプロ解説
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#文章題#売買損益と食塩水#平面図形#角度と面積
指導講師：
重吉
問題文全文(内容文)：
※図は動画内参照
次の計算をしなさい。
(1)
$1446 \div 6 \times 2-165\div 15$
(2)
$\dfrac{2}{15}-\{ (6\div 2.25-2\dfrac{5}{8}\div 4.5) \times0.2-\dfrac{1}{3}\}$
2
一辺の長さが20 cmの正方形を、図に書かれた面積になるように、4つの長方形に分けました。このとき、Aの長さを求めなさい。
３
ある食塩水に、食塩20 gと水80 gを加えたので、濃度10 %の食塩水が500 gできました。もとの食塩水の濃度は何%ですか。
４
消しゴム2個の値段は、鉛筆3本の値段より10円高く、消しゴム6個と鉛筆5本を買うと、代金は1010円になります。消しゴム1個の値段はいくらですか。
この動画を見る
※図は動画内参照
次の計算をしなさい。
(1)
$1446 \div 6 \times 2-165\div 15$
(2)
$\dfrac{2}{15}-\{ (6\div 2.25-2\dfrac{5}{8}\div 4.5) \times0.2-\dfrac{1}{3}\}$
2
一辺の長さが20 cmの正方形を、図に書かれた面積になるように、4つの長方形に分けました。このとき、Aの長さを求めなさい。
３
ある食塩水に、食塩20 gと水80 gを加えたので、濃度10 %の食塩水が500 gできました。もとの食塩水の濃度は何%ですか。
４
消しゴム2個の値段は、鉛筆3本の値段より10円高く、消しゴム6個と鉛筆5本を買うと、代金は1010円になります。消しゴム1個の値段はいくらですか。
2024年東洋英和女学院中算数大問①（１）～（４）中学受験指導歴２０年以上のプロ解説
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#文章題#売買損益と食塩水#平均算・過不足算・差集め算・消去算#平面図形#角度と面積
指導講師：
重吉
問題文全文(内容文)：
１．次の計算をしなさい。
(1) $144\div6\times2-165\div15$
(2) $\dfrac{2}{15}-\{ (6\div2.25-2\dfrac{5}{8}\div4.5)\times0.2-\dfrac{1}{3} \}$
２．一辺の長さが20 cmの正方形を、図に書かれた面積になるように、四つの長方形に分けました。このとき、Aの長さを求めなさい。
※図は動画内参照
３．ある食塩水に、食塩20 gと水80 gを加えたので、濃度10 %の食塩水が500 gできました。もとの食塩水の濃度は何%ですか。
４．消しゴム2個の値段は、鉛筆3本の値段より10円高く、消しゴム6個と鉛筆5本を買うと、代金は1010円になります。消しゴム1個の値段はいくらですか。
この動画を見る
１．次の計算をしなさい。
(1) $144\div6\times2-165\div15$
(2) $\dfrac{2}{15}-\{ (6\div2.25-2\dfrac{5}{8}\div4.5)\times0.2-\dfrac{1}{3} \}$
２．一辺の長さが20 cmの正方形を、図に書かれた面積になるように、四つの長方形に分けました。このとき、Aの長さを求めなさい。
※図は動画内参照
３．ある食塩水に、食塩20 gと水80 gを加えたので、濃度10 %の食塩水が500 gできました。もとの食塩水の濃度は何%ですか。
４．消しゴム2個の値段は、鉛筆3本の値段より10円高く、消しゴム6個と鉛筆5本を買うと、代金は1010円になります。消しゴム1個の値段はいくらですか。
2024年早稲田実業中算数大問①（１）～（４）中学受験指導歴２０年以上のプロ解説
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#文章題#売買損益と食塩水#平面図形#角度と面積#場合の数#場合の数#早稲田実業中等部
指導講師：
問題文全文(内容文)：
(1)$20\dfrac{24}{25}-(0.175\times11\dfrac{3}{7}+4\dfrac{1}{18}\div\Box)\times0.18=6$の▭に当てはまる数を求めなさい。
(2)6人グループの中から班長1人、副班長2人を選びます。選び方は全部で何通りありますか。
(3)下の図の㋐の角度を求めなさい。
※図は動画内参照
(4)容器Aには濃度6 %の食塩水が300 g、容器Bには濃度15 %の食塩水が500 g入っています。この二つの容器から同じ量を同時にくみ出して、容器Aからくみだした分を容器Bに、容器Bからくみだした分を容器Aに入れてそれぞれ混ぜ合わせたところ、容器Aの食塩水の濃度は9 %になりました。混ぜ合わせた後の容器Bの食塩水の濃度を求めなさい。
この動画を見る
(1)$20\dfrac{24}{25}-(0.175\times11\dfrac{3}{7}+4\dfrac{1}{18}\div\Box)\times0.18=6$の▭に当てはまる数を求めなさい。
(2)6人グループの中から班長1人、副班長2人を選びます。選び方は全部で何通りありますか。
(3)下の図の㋐の角度を求めなさい。
※図は動画内参照
(4)容器Aには濃度6 %の食塩水が300 g、容器Bには濃度15 %の食塩水が500 g入っています。この二つの容器から同じ量を同時にくみ出して、容器Aからくみだした分を容器Bに、容器Bからくみだした分を容器Aに入れてそれぞれ混ぜ合わせたところ、容器Aの食塩水の濃度は9 %になりました。混ぜ合わせた後の容器Bの食塩水の濃度を求めなさい。
2024年豊島岡女子学園中算数大問①（１）～（４）中学受験指導歴２０年以上のプロ解説
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#規則性（周期算・方陣算・数列・日暦算・N進法）#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#平均算・過不足算・差集め算・消去算#豊島岡女子学園中学
指導講師：
重吉
問題文全文(内容文)：
次の各問いに答えなさい。
(1)$2024\div3\times\{ (0.32+\dfrac{2}{5})\div\dfrac{4}{15}\div9.9 \}$を計算しなさい。
(2)中学1年生に用意した鉛筆を配りました。1人に3本ずつ配ると88本あまり、1人に5本ずつ配ると4本不足しました。用意したえんぴつは全部で何本でしたか。
(3)Aさんの所持金の半分の金額と、Bさんの所持金の40 %の金額は同じ金額です。また、Aさんの所持金に1800円を加えた金額とBさんの所持金の2倍の金額は同じ金額です。Aさんの所持金はいくらですか。
(4)下の図の〇の中に1から10までの異なる整数を書き入れ、（あ）から（け）までの9つの三角形の頂点の3つの数を足します。このようにしてできた9つの数の和が最も小さくなるような数を書き入れるとき、その和を答えなさい。
※図は動画内参照
この動画を見る
次の各問いに答えなさい。
(1)$2024\div3\times\{ (0.32+\dfrac{2}{5})\div\dfrac{4}{15}\div9.9 \}$を計算しなさい。
(2)中学1年生に用意した鉛筆を配りました。1人に3本ずつ配ると88本あまり、1人に5本ずつ配ると4本不足しました。用意したえんぴつは全部で何本でしたか。
(3)Aさんの所持金の半分の金額と、Bさんの所持金の40 %の金額は同じ金額です。また、Aさんの所持金に1800円を加えた金額とBさんの所持金の2倍の金額は同じ金額です。Aさんの所持金はいくらですか。
(4)下の図の〇の中に1から10までの異なる整数を書き入れ、（あ）から（け）までの9つの三角形の頂点の3つの数を足します。このようにしてできた9つの数の和が最も小さくなるような数を書き入れるとき、その和を答えなさい。
※図は動画内参照
2024年青山学院中等部算数大問①～⑤ 中学受験指導歴２０年以上のプロ解説
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#文章題#単位・比と割合・比例・反比例#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#平均算・過不足算・差集め算・消去算#青山学院中等部
指導講師：
重吉
問題文全文(内容文)：
$\Box$に当てはまる数を入れなさい。円周率を使う場合は3.14とします。
(1)$28-3\times(65-52\div13\times14)+2=\Box$
(2)$(1.05\div1\dfrac{2}{5}-0.11\times\Box)\div\dfrac{2}{7}=0.7$
(3)袋にお菓子がいくつか入っています。この袋から兄は全体の20 %分の個数を取りました。次に、弟と妹がその残りからそれぞれ25 %分と30 %分の個数を取りました。袋に入っているお菓子の個数は、はじめの個数の$\Box$%です。
(4)ラグビー部の昨年の部員数は30人でした。今年の1年生は昨年の1年生の2倍の人数が入部し、今年の3年生の人数は昨年の3年生の$\dfrac{6}{5}$倍の人数なので、今年の部員数は36人になりました。今年入部した1年生の人数は$\Box$人です。ただし、学年の途中で退部した生徒はいないものとします。
(5)花子さんは1個80円のりんご、1個120円の梨、1個160円の柿を合わせて46個買ったところ、代金は6160円でした。花子さんが買ったりんごと柿の個数の比が1:3のとき、梨の個数は$\Box$個です。
この動画を見る
$\Box$に当てはまる数を入れなさい。円周率を使う場合は3.14とします。
(1)$28-3\times(65-52\div13\times14)+2=\Box$
(2)$(1.05\div1\dfrac{2}{5}-0.11\times\Box)\div\dfrac{2}{7}=0.7$
(3)袋にお菓子がいくつか入っています。この袋から兄は全体の20 %分の個数を取りました。次に、弟と妹がその残りからそれぞれ25 %分と30 %分の個数を取りました。袋に入っているお菓子の個数は、はじめの個数の$\Box$%です。
(4)ラグビー部の昨年の部員数は30人でした。今年の1年生は昨年の1年生の2倍の人数が入部し、今年の3年生の人数は昨年の3年生の$\dfrac{6}{5}$倍の人数なので、今年の部員数は36人になりました。今年入部した1年生の人数は$\Box$人です。ただし、学年の途中で退部した生徒はいないものとします。
(5)花子さんは1個80円のりんご、1個120円の梨、1個160円の柿を合わせて46個買ったところ、代金は6160円でした。花子さんが買ったりんごと柿の個数の比が1:3のとき、梨の個数は$\Box$個です。
2024年慶應義塾湘南藤沢中算数大問①② 中学受験指導２０年以上のプロ解説
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#過去問解説(学校別)#文章題#売買損益と食塩水#平面図形#角度と面積#速さ#旅人算・通過算・流水算#慶應義塾湘南藤沢中等部
指導講師：
重吉
問題文全文(内容文)：
【1】$\boxed{ア}$, $\boxed{イ}$, $\boxed{ウ}$にあてはまる数を求めなさい。
(1)$10-(20.24+17\dfrac{\boxed{ ア }}{25})\div9=5\dfrac{4}{5}$
(2)$\dfrac{1}{3\times6}+\dfrac{1}{6\times9}+\dfrac{1}{9\times12}+\dfrac{1}{12\times15}+\dfrac{1}{15\times18}=\boxed{イ}$
(3)1から100までの数から4の倍数と6の倍数を除いた数は全部で$\boxed{ウ}$個である。
【2】
(1)1周672 mの池の周りを、K君、O君の二人が同じ地点から同時に出発し、それぞれ一定の速さで歩く。二人が反対方向に歩く場合は6分後に初めて出会い、2人が同じ方向に歩く場合は42分後にK君がO君を初めて追い越す。K君の歩く速さは毎分何mですか。
(2)毎日決まった数だけ売れる1個150円の品物がある。今、売上を20円値上げしたところ、1日の売り上げ個数は1割減少したが、売上高は180円増加した。この品物の、値上げ前の1日の売り上げ個数は何個ですか。
(3)図のような長方形において、角㋐の大きさを求めなさい。
※図は動画内参照
この動画を見る
【1】$\boxed{ア}$, $\boxed{イ}$, $\boxed{ウ}$にあてはまる数を求めなさい。
(1)$10-(20.24+17\dfrac{\boxed{ ア }}{25})\div9=5\dfrac{4}{5}$
(2)$\dfrac{1}{3\times6}+\dfrac{1}{6\times9}+\dfrac{1}{9\times12}+\dfrac{1}{12\times15}+\dfrac{1}{15\times18}=\boxed{イ}$
(3)1から100までの数から4の倍数と6の倍数を除いた数は全部で$\boxed{ウ}$個である。
【2】
(1)1周672 mの池の周りを、K君、O君の二人が同じ地点から同時に出発し、それぞれ一定の速さで歩く。二人が反対方向に歩く場合は6分後に初めて出会い、2人が同じ方向に歩く場合は42分後にK君がO君を初めて追い越す。K君の歩く速さは毎分何mですか。
(2)毎日決まった数だけ売れる1個150円の品物がある。今、売上を20円値上げしたところ、1日の売り上げ個数は1割減少したが、売上高は180円増加した。この品物の、値上げ前の1日の売り上げ個数は何個ですか。
(3)図のような長方形において、角㋐の大きさを求めなさい。
※図は動画内参照
2024年海城中算数大問①（１）～（５）中学受験指導歴２０年以上のプロ解説
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#文章題#売買損益と食塩水#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#平面図形#角度と面積
指導講師：
重吉
問題文全文(内容文)：
(1)
$9\div\{4\dfrac{1}{6}+(2.25-1\dfrac{1}{2})\div0.75-2\dfrac{1}{2}\}\div1.125$を計算しなさい。
(2)
8%の食塩水を80g、6%の食塩水を120g、4%の食塩水を150g、水▭gを混ぜて5%の食塩水を作りました。▭に当てはまる数を求めなさい。
(3)
現在、父の年齢は兄の年齢の3倍と弟の年齢の和より4歳上です。24年後ｍ父の年齢は兄と弟の年齢の和に等しくなります。父と弟の年齢の差を求めなさい。
(4)
100以上300以下の整数のうち、約数の個数が9個である整数をすべて求めなさい。
(5)
下の図において直線ABとCDは平行で、長さの等しい辺には同じ印がついています。図の角アの大きさを求めなさい。
※図は動画内参照図
この動画を見る
(1)
$9\div\{4\dfrac{1}{6}+(2.25-1\dfrac{1}{2})\div0.75-2\dfrac{1}{2}\}\div1.125$を計算しなさい。
(2)
8%の食塩水を80g、6%の食塩水を120g、4%の食塩水を150g、水▭gを混ぜて5%の食塩水を作りました。▭に当てはまる数を求めなさい。
(3)
現在、父の年齢は兄の年齢の3倍と弟の年齢の和より4歳上です。24年後ｍ父の年齢は兄と弟の年齢の和に等しくなります。父と弟の年齢の差を求めなさい。
(4)
100以上300以下の整数のうち、約数の個数が9個である整数をすべて求めなさい。
(5)
下の図において直線ABとCDは平行で、長さの等しい辺には同じ印がついています。図の角アの大きさを求めなさい。
※図は動画内参照図
2024年筑波大附属中算数「公約数」中学受験指導歴20年以上のプロ解説
単元：
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#文章題#文章題その他
指導講師：
重吉
問題文全文(内容文)：
えんぴつ136本、消しゴム187個、ノート343冊があります。
これらを何人かの子どもにそれぞれ同じ数ずつ分けると、えんぴつは8本不足し、消しゴムは7個あまり、ノートは19冊あまりました。
分けるときは、子どもの人数よりも多くあまりがでないように分けています。このとき、子どもの人数は何人ですか。
この動画を見る
えんぴつ136本、消しゴム187個、ノート343冊があります。
これらを何人かの子どもにそれぞれ同じ数ずつ分けると、えんぴつは8本不足し、消しゴムは7個あまり、ノートは19冊あまりました。
分けるときは、子どもの人数よりも多くあまりがでないように分けています。このとき、子どもの人数は何人ですか。
平均算（標準・発展）をサクッと学習しよう！【中学受験算数】【特殊算攻略講座２２】
単元：
#算数(中学受験)#文章題#平均算・過不足算・差集め算・消去算
指導講師：
こばちゃん塾
問題文全文(内容文)：
問題1
ある小学校の生徒12人の身長を調べた結果、次のようになりました。
このとき、この12人の身長の平均を求めましょう。
問題2
A小学校とB小学校の生徒数はあわせて200人で、A小学校の生徒の通学時間の平均は17分、
B小学校の生徒の通学時間の平均は9分です。また、A小学校とB小学校の生徒をあわせると通学
時間の平均は14分になりました。A小学校の生徒は何人ですか？
＊図は動画内参照
この動画を見る
問題1
ある小学校の生徒12人の身長を調べた結果、次のようになりました。
このとき、この12人の身長の平均を求めましょう。
問題2
A小学校とB小学校の生徒数はあわせて200人で、A小学校の生徒の通学時間の平均は17分、
B小学校の生徒の通学時間の平均は9分です。また、A小学校とB小学校の生徒をあわせると通学
時間の平均は14分になりました。A小学校の生徒は何人ですか？
＊図は動画内参照
2024年栄東中（A）算数大問①（５）～（８）中学受験指導歴２０年以上のプロ解説
単元：
#算数(中学受験)#過去問解説(学校別)#文章題#仕事算とニュートン算#平面図形#角度と面積#相似と相似を利用した問題#立体図形#体積・表面積・回転体・水量・変化のグラフ#栄東中学
指導講師：
重吉
問題文全文(内容文)：
(5) ある仕事をするのに、赤いロボット1体では24時間かかります。また、紫のロボットは赤いロボットの10倍の仕事ができます。合わせて18台のロボットがこの仕事をしたところ、20分でおわりました。このとき、赤いロボットは▭体でした。
(6) 右の図のように三角形をABCの辺AC上に点Dがあり、ABとADの長さは等しく、イの角度はアの角度の2倍で、ウの角度はアの角度の6倍です。このとき、エの角度は▭度です。
※図は動画内参照
(7) 右の図のように直角三角形ABCの紙をADを折り目として折り返したところ、点BがAC上の点Eに重なりました。このとき、三角形ABCの面積は▭㎠です。
※図は動画内参照
(8) 右の図のようにAB = BC = 3 cmの直角二等辺三角形二等辺三角形ABCを直線DEを軸に一回転させたときにできる立体の体積は▭㎤です。ただし、円周率は3.14とします。必要であれば、円錐の体積は「（底面積）×（高さ）÷3」で求められることを使っても構いません。
この動画を見る
(5) ある仕事をするのに、赤いロボット1体では24時間かかります。また、紫のロボットは赤いロボットの10倍の仕事ができます。合わせて18台のロボットがこの仕事をしたところ、20分でおわりました。このとき、赤いロボットは▭体でした。
(6) 右の図のように三角形をABCの辺AC上に点Dがあり、ABとADの長さは等しく、イの角度はアの角度の2倍で、ウの角度はアの角度の6倍です。このとき、エの角度は▭度です。
※図は動画内参照
(7) 右の図のように直角三角形ABCの紙をADを折り目として折り返したところ、点BがAC上の点Eに重なりました。このとき、三角形ABCの面積は▭㎠です。
※図は動画内参照
(8) 右の図のようにAB = BC = 3 cmの直角二等辺三角形二等辺三角形ABCを直線DEを軸に一回転させたときにできる立体の体積は▭㎤です。ただし、円周率は3.14とします。必要であれば、円錐の体積は「（底面積）×（高さ）÷3」で求められることを使っても構いません。
この計算方法知ってる？
【小6算数手元解説】切るのに8分そして2分休む【問題文は概要欄】
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
長さ3mの木材を端から20cmと10cmの長さに交互に切り取りました。1回切るのに8分かかり、1回切ると2分間ずつ休むことにします。全部切り終わるのに何分かかりますか。
この動画を見る
長さ3mの木材を端から20cmと10cmの長さに交互に切り取りました。1回切るのに8分かかり、1回切ると2分間ずつ休むことにします。全部切り終わるのに何分かかりますか。
2024年青山学院中等部算数「底面積と体積の比」中学受験指導歴20年以上のプロ解説
単元：
#算数(中学受験)#過去問解説(学校別)#文章題#単位・比と割合・比例・反比例#仕事算とニュートン算#立体図形#体積・表面積・回転体・水量・変化のグラフ#青山学院中等部
指導講師：
重吉
問題文全文(内容文)：
円柱の形をした2つの容器A,Bがあります。
A,Bともに同じ一定の割合で水を入れると、入れ始めてからAは28分で、Bは36分でいっぱいになります。
今、両方の容器をいっぱいにしてから、入れるときと同じ水量で底から同時に水を出したところ12分後に2つの容器の水面の高さは等しくなりました。
AとBの底面の面積の比は$\Box:\Box$で、高さの比は$\Box:\Box$です。
この動画を見る
円柱の形をした2つの容器A,Bがあります。
A,Bともに同じ一定の割合で水を入れると、入れ始めてからAは28分で、Bは36分でいっぱいになります。
今、両方の容器をいっぱいにしてから、入れるときと同じ水量で底から同時に水を出したところ12分後に2つの容器の水面の高さは等しくなりました。
AとBの底面の面積の比は$\Box:\Box$で、高さの比は$\Box:\Box$です。
2024年青山学院中等部算数「底面積と体積の比」中学受験指導歴20年以上のプロ解説
単元：
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師：
重吉
問題文全文(内容文)：
円柱の形をした2つの容器A、Bがあります。
A、Bともに同じ一定の割合で水を入れると、入れ始めてからAは28分で、Bは36分でいっぱいになります。
今、両方の容器をいっぱいにしてから、入れるときと同じ水量で底から同時に水を出したところ12分後に2つの容器の水面の高さは等しくなりました。
AとBの底面の面積の比は何対何で、高さの比は何対何です。
この動画を見る
円柱の形をした2つの容器A、Bがあります。
A、Bともに同じ一定の割合で水を入れると、入れ始めてからAは28分で、Bは36分でいっぱいになります。
今、両方の容器をいっぱいにしてから、入れるときと同じ水量で底から同時に水を出したところ12分後に2つの容器の水面の高さは等しくなりました。
AとBの底面の面積の比は何対何で、高さの比は何対何です。
【小6算数手元解説】赤・青・黄リングを順につなぐ【問題文は概要欄】
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
下図のような、同じ大きさの赤、青、黄のリングをつなぎます。
（１）赤、青、黄の3つのリングをつなぐと長さは何cmですか。
（２）赤→青→黄→赤→青→・・・の順にリングをつないでいって、長さ194cmのくさりを作りたいと思います。この時、最後につなぐリングの色は何色ですか
（３）赤→青→黄→赤→青→・・・の順にリングをつないで、黄を13個使ったときにもっとも長くなるくさりの長さは何cmですか。
この動画を見る
下図のような、同じ大きさの赤、青、黄のリングをつなぎます。
（１）赤、青、黄の3つのリングをつなぐと長さは何cmですか。
（２）赤→青→黄→赤→青→・・・の順にリングをつないでいって、長さ194cmのくさりを作りたいと思います。この時、最後につなぐリングの色は何色ですか
（３）赤→青→黄→赤→青→・・・の順にリングをつないで、黄を13個使ったときにもっとも長くなるくさりの長さは何cmですか。
2024年鷗友学園女子中算数「比」中学受験指導歴20年以上のプロ解説
単元：
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
指導講師：
重吉
問題文全文(内容文)：
Aさん、Bさん、Cさん の3人でお金を出しあって9200円のプレゼントを買います。
最初、3人の所持金の比は15:2:8でしたが、 AさんがBさんに400円渡し、CさんもBさんにいくらか渡すと、所持金の比は8:3:3になりまし
この後、プレゼントを買いました。
(1)所持金の比が8:3:3になったとき、Aさんの所持金はいくらになりましたか?
(2)プレゼントを買った後、3人の所持金の比は
5:3:2になりました。Cさんがプレゼントを
買うために出した金額はいくらですか。
この動画を見る
Aさん、Bさん、Cさん の3人でお金を出しあって9200円のプレゼントを買います。
最初、3人の所持金の比は15:2:8でしたが、 AさんがBさんに400円渡し、CさんもBさんにいくらか渡すと、所持金の比は8:3:3になりまし
この後、プレゼントを買いました。
(1)所持金の比が8:3:3になったとき、Aさんの所持金はいくらになりましたか?
(2)プレゼントを買った後、3人の所持金の比は
5:3:2になりました。Cさんがプレゼントを
買うために出した金額はいくらですか。
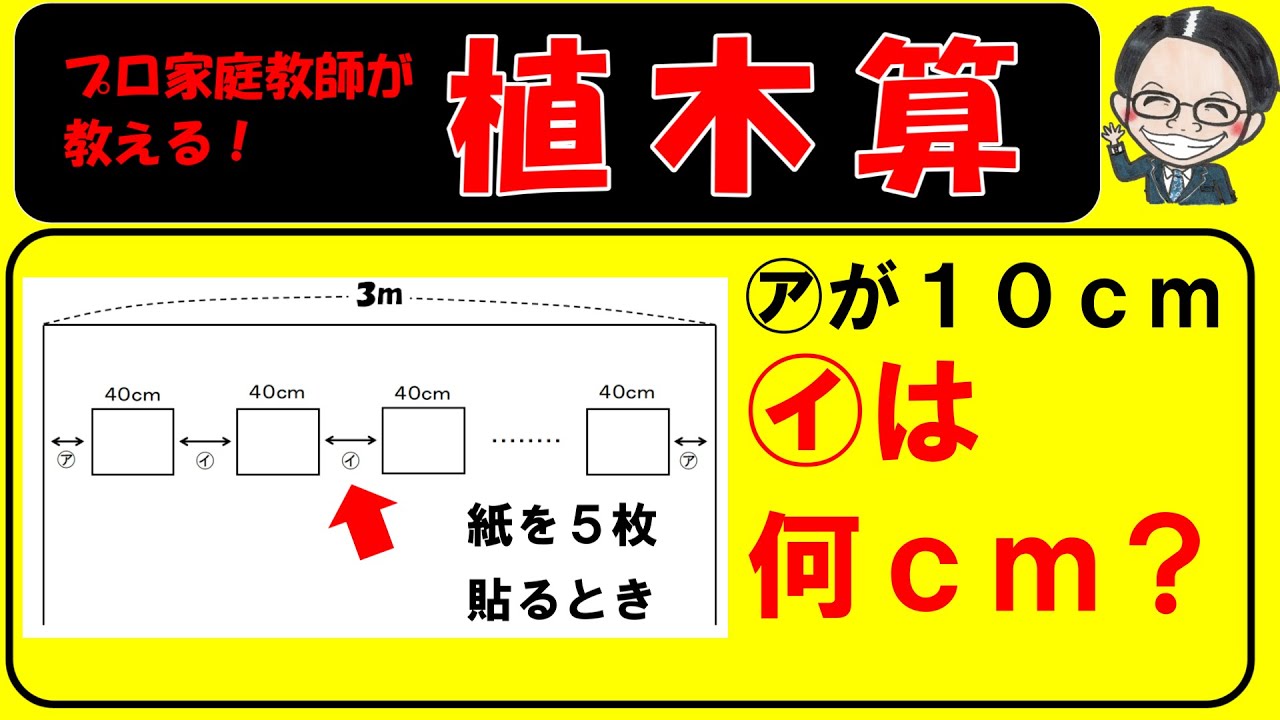
植木算（標準・発展）をサクッと学習しよう！【中学受験算数】【特殊算攻略講座２１】
単元：
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師：
こばちゃん塾
問題文全文(内容文)：
下図のように、はばが3mある掲示板に横の長さが40㎝の絵を
絵と絵の間をどこも同じ長さにして5枚はります。
かべの端と絵の間（図の㋐）の長さを10㎝にすると、
絵と絵の間（図の㋑）の長さは何㎝になりますか。
＊図は動画内参照
この動画を見る
下図のように、はばが3mある掲示板に横の長さが40㎝の絵を
絵と絵の間をどこも同じ長さにして5枚はります。
かべの端と絵の間（図の㋐）の長さを10㎝にすると、
絵と絵の間（図の㋑）の長さは何㎝になりますか。
＊図は動画内参照
2024年明治大付属明治中算数「食塩水濃度」中学受験指導歴20年以上のプロ解説
単元：
#算数(中学受験)#文章題#売買損益と食塩水
指導講師：
重吉
問題文全文(内容文)：
容器$A$には6%の食塩水が300g,容器$B$には12%の食塩水が500g入っています.
両方の容器から同じ量の食塩水を同時に取り出し,それぞれもう一方の容器に入れたところ,
$A$に入っている食塩水の濃さは10%になりました.
$B$に入っている食塩水の濃さは$\Box$になります.
$\Box$を求めよ.
2024年明治大付属明治中過去問
この動画を見る
容器$A$には6%の食塩水が300g,容器$B$には12%の食塩水が500g入っています.
両方の容器から同じ量の食塩水を同時に取り出し,それぞれもう一方の容器に入れたところ,
$A$に入っている食塩水の濃さは10%になりました.
$B$に入っている食塩水の濃さは$\Box$になります.
$\Box$を求めよ.
2024年明治大付属明治中過去問
2024年明治大付属明治中算数「食塩水濃度」中学受験指導歴20年以上のプロ解説
単元：
#算数(中学受験)#過去問解説(学校別)#文章題#売買損益と食塩水#明治大学附属明治中学
指導講師：
重吉
問題文全文(内容文)：
容器Aには6%の食塩水が300g、容器Bには12%の食塩水が500g入っています。
両方の容器から同じ量の食塩水を同時に取り出し、それぞれもう一方の容器に入れたところ、Aに入っている食塩水の濃さは10%になりました。
Bに入っている食塩水の濃さは□%になります。
出典：2024年明治大学付属明治中学校 入試問題
この動画を見る
容器Aには6%の食塩水が300g、容器Bには12%の食塩水が500g入っています。
両方の容器から同じ量の食塩水を同時に取り出し、それぞれもう一方の容器に入れたところ、Aに入っている食塩水の濃さは10%になりました。
Bに入っている食塩水の濃さは□%になります。
出典：2024年明治大学付属明治中学校 入試問題
2024年立教新座中算数「和差算」中学受験指導歴20年のプロ解説
単元：
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師：
重吉
問題文全文(内容文)：
$4$つの異なる整数,$A,B,C,D$があります.
これらの整数のうち異なる2つをたすと全部で6つの数ができますが,この6つの数の中に同じ数が
あったので,できた数は$10,13,15,17,20$の5種類でした.4つの整数$A,B,C,D$の積をもとめなさい.
2024年立教新座中過去問
この動画を見る
$4$つの異なる整数,$A,B,C,D$があります.
これらの整数のうち異なる2つをたすと全部で6つの数ができますが,この6つの数の中に同じ数が
あったので,できた数は$10,13,15,17,20$の5種類でした.4つの整数$A,B,C,D$の積をもとめなさい.
2024年立教新座中過去問
2024年立教新座中算数「和差算」中学受験指導歴20年のプロ解説
単元：
#算数(中学受験)#過去問解説(学校別)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#立教新座中学
指導講師：
重吉
問題文全文(内容文)：
4つの異なる整数A,B,C,Dがあります。
これらの整数のうち異なる2つをたすと全部で6つの数ができますが、この6つの数の中に同じ数があったので、できた数は10,13,15,17,20の5種類でした。
4つの整数A,B,C,Dの積を求めなさい。
出典：2024年立教新座中学校 入試問題
この動画を見る
4つの異なる整数A,B,C,Dがあります。
これらの整数のうち異なる2つをたすと全部で6つの数ができますが、この6つの数の中に同じ数があったので、できた数は10,13,15,17,20の5種類でした。
4つの整数A,B,C,Dの積を求めなさい。
出典：2024年立教新座中学校 入試問題
あなたはどの道を通りますか？
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#文章題
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
あなたはどの道を通りますか？
【問題文】
かおりさんの家から学校までは、㋐～㋒の3つの道があります。
あなたなら、どの道を通りますか。
1つえらび、そのわけを書きましょう。
※図は動画内参照
この動画を見る
あなたはどの道を通りますか？
【問題文】
かおりさんの家から学校までは、㋐～㋒の3つの道があります。
あなたなら、どの道を通りますか。
1つえらび、そのわけを書きましょう。
※図は動画内参照
どの道を通りますか？に対する解答が話題になっている件
単元：
#算数(中学受験)#計算と数の性質#文章題
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
どの道を通りますか？に対する解答が話題になっている件
【問題文】
かおりさんの家から学校までは、㋐～㋒の3つの道があります。
あなたなら、どの道を通りますか。
1つえらび、そのわけを書きましょう。
この動画を見る
どの道を通りますか？に対する解答が話題になっている件
【問題文】
かおりさんの家から学校までは、㋐～㋒の3つの道があります。
あなたなら、どの道を通りますか。
1つえらび、そのわけを書きましょう。
2024年洗足学園中算数「相当算」中学受験指導歴20年のプロ解説
単元：
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師：
重吉
問題文全文(内容文)：
(1)はじめの所持金を求めよ.
(2)2番目の店に行った時の所持金を求めよ.
(3)3番目のみ背に行った時の所持金を求めよ.
2024年洗足学園中過去問
この動画を見る
(1)はじめの所持金を求めよ.
(2)2番目の店に行った時の所持金を求めよ.
(3)3番目のみ背に行った時の所持金を求めよ.
2024年洗足学園中過去問
2024年洗足学園中算数「相当算」中学受験指導歴20年のプロ解説
単元：
#算数(中学受験)#過去問解説(学校別)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#洗足学園中学
指導講師：
重吉
問題文全文(内容文)：
Aさんが買い物をしました。
最初の店では所持金の$\displaystyle \frac{1}{2}$より200円多く使い、2番目の店では残った所持金の$\displaystyle \frac{1}{3}$よりも400円多く使いました。
3番目の店で残った所持金の$\displaystyle \frac{1}{4}$よりも600円多く使ったところ、所持金をすべて使い切りました。
Aさんは、はじめに何円持っていましたか。
出典：2024年洗足学園中学高等学校 入試問題
この動画を見る
Aさんが買い物をしました。
最初の店では所持金の$\displaystyle \frac{1}{2}$より200円多く使い、2番目の店では残った所持金の$\displaystyle \frac{1}{3}$よりも400円多く使いました。
3番目の店で残った所持金の$\displaystyle \frac{1}{4}$よりも600円多く使ったところ、所持金をすべて使い切りました。
Aさんは、はじめに何円持っていましたか。
出典：2024年洗足学園中学高等学校 入試問題