 場合の数
場合の数
 場合の数
場合の数
【受験算数】右の図は、正方形の中に三角形をかいたものです。色のついた部分の面積は何㎠ですか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図は、正方形の中に三角形をかいたものです。
色のついた部分の面積は何㎠ですか。
この動画を見る
右の図は、正方形の中に三角形をかいたものです。
色のついた部分の面積は何㎠ですか。
【受験算数】野球の大会に40チームが出場します。大会は、はじめに5チームずつのグループに分かれて、 各グループごとにリーグ戦で予選が行われます。そして、各グループの上位2チームずつが本戦に勝ち残り…

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
野球の大会に40チームが出場します。大会は、はじめに5チームずつのグループに分かれて、 各グループごとにリーグ戦で予選が行われます。そして、各グループの上位2チームずつが本戦に勝ち残り、本戦はトーナメント戦で優勝が決まります。この大会では、全部で何試合行われますか。ただし、予選のリーグ戦は、グループ内の他のチームと1試合ずつ行います。また、 どの試合も引き分けはなく、3位決定戦などは行わないものとします。
この動画を見る
野球の大会に40チームが出場します。大会は、はじめに5チームずつのグループに分かれて、 各グループごとにリーグ戦で予選が行われます。そして、各グループの上位2チームずつが本戦に勝ち残り、本戦はトーナメント戦で優勝が決まります。この大会では、全部で何試合行われますか。ただし、予選のリーグ戦は、グループ内の他のチームと1試合ずつ行います。また、 どの試合も引き分けはなく、3位決定戦などは行わないものとします。
【受験算数】1, 1, 2, 3, 4, 5 の6枚のカードがあります。この中から3枚を取り出してならべ。3けたの整数を作ります。これについて、次の問いに答えなさい。4の倍数は何通りできますか…

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
1, 1, 2, 3, 4, 5 の6枚のカードがあります。この中から3枚を取り出してならべ。3けたの整数を作ります。これについて、次の問いに答えなさい。
(1)4の倍数は何通りできますか。
(2)3の倍数は何通りできますか。
この動画を見る
1, 1, 2, 3, 4, 5 の6枚のカードがあります。この中から3枚を取り出してならべ。3けたの整数を作ります。これについて、次の問いに答えなさい。
(1)4の倍数は何通りできますか。
(2)3の倍数は何通りできますか。
【受験算数】A, B, C, D, E, F, Gの7人が旅行に行き、旅館にとまることになりました。旅館では、3人がとまれる「鶴の間」と、4人がとまれる「亀の間」の2部屋に分かれてとまることにします…

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
A, B, C, D, E, F, Gの7人が旅行に行き、旅館にとまることになりました。旅館では、3人がとまれる「鶴の間」と、4人がとまれる「亀の間」の2部屋に分かれてとまることにします。これについて、次の問いに答えなさい。
(1)とまり方は何通りありますか。
(2)AとBが同じ部屋になるとまり方は何通りありますか。
この動画を見る
A, B, C, D, E, F, Gの7人が旅行に行き、旅館にとまることになりました。旅館では、3人がとまれる「鶴の間」と、4人がとまれる「亀の間」の2部屋に分かれてとまることにします。これについて、次の問いに答えなさい。
(1)とまり方は何通りありますか。
(2)AとBが同じ部屋になるとまり方は何通りありますか。
【受験算数】5枚の同じコインを、A, B, Cの3人で分けます。(1)全員、必ず1枚はもらえるとすると、分け方は何通りありますか(2) 1枚ももらえない人がいてもよいとすると、分け方は何通りありますか

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
5枚の同じコインを、A, B, Cの3人で分けます。これについて、次の問いに答えなさい。
(1)全員、必ず1枚はもらえるとすると、分け方は何通りありますか。
(2) 1枚ももらえない人がいてもよいとすると、分け方は何通りありますか。
この動画を見る
5枚の同じコインを、A, B, Cの3人で分けます。これについて、次の問いに答えなさい。
(1)全員、必ず1枚はもらえるとすると、分け方は何通りありますか。
(2) 1枚ももらえない人がいてもよいとすると、分け方は何通りありますか。
【受験算数】右の図で、5つの直線ア、イ、ウ、エ、オは互いに平行で、4つの直線力、キ、ク、ケは互いに平行です。この図の中に平行四辺形は何個ありますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図で、5つの直線ア、イ、ウ、エ、オは互いに平行で、4つの直線力、キ、ク、ケは互いに平行です。この図の中に平行四辺形は何個ありますか。
この動画を見る
右の図で、5つの直線ア、イ、ウ、エ、オは互いに平行で、4つの直線力、キ、ク、ケは互いに平行です。この図の中に平行四辺形は何個ありますか。
【受験算数】A, B, C, D, E, F, Gの7人の男子とP, Q, R, Sの4人の女子がいます。男子から3人、女子から2人の合計5人を音楽係として選ぶ方法は何通りありますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
A, B, C, D, E, F, Gの7人の男子とP, Q, R, Sの4人の女子がいます。
これについて、次の問いに答えなさい。
(1) 男子から3人、女子から2人の合計5人を音楽係として選ぶ方法は何通りありますか。
(2)この11人を、指揮者1人、リコーダー担当8人、ハーモニカ担当2人に分けるとき、分け方は何通りありますか。
この動画を見る
A, B, C, D, E, F, Gの7人の男子とP, Q, R, Sの4人の女子がいます。
これについて、次の問いに答えなさい。
(1) 男子から3人、女子から2人の合計5人を音楽係として選ぶ方法は何通りありますか。
(2)この11人を、指揮者1人、リコーダー担当8人、ハーモニカ担当2人に分けるとき、分け方は何通りありますか。
【受験算数】右の図のような16個の空らんに0以上の整数を記入して、たて、横に加えた和が、らん外に記したA、1、1、1になるようにして表を作る。A=0とすると、この表は何通りできるか。

単元:
#算数(中学受験)#場合の数#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のような16個の空らんに0以上の整数を記入して、たて、横に加えた和が、らん外に記したA、1、1、1になるようにして表を作る。
(1)A=0とすると、この表は何通りできるか。
(2)A=1とすると、この表は何通りできるか。
(3)A=2とすると、この表は何通りできるか。
(4)A=3とすると、この表は何通りできるか。
この動画を見る
右の図のような16個の空らんに0以上の整数を記入して、たて、横に加えた和が、らん外に記したA、1、1、1になるようにして表を作る。
(1)A=0とすると、この表は何通りできるか。
(2)A=1とすると、この表は何通りできるか。
(3)A=2とすると、この表は何通りできるか。
(4)A=3とすると、この表は何通りできるか。
【受験算数】何人かの生徒が、いすに横一列に座っている。これから座り方を変えようと思う。全員が今までとは異なるいすに座る座り方は何通りあるか。以下のそれぞれの人数の場合について答えよ。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
何人かの生徒が、いすに横一列に座っている。これから座り方を変えようと思う。全員が今までとは異なるいすに座る座り方は何通りあるか。以下のそれぞれの人数の場合について答えよ。ただし、いすは人数と同じ数だけある。
(1)3人のとき。
(2)4人のとき。
(3)5人のとき。
この動画を見る
何人かの生徒が、いすに横一列に座っている。これから座り方を変えようと思う。全員が今までとは異なるいすに座る座り方は何通りあるか。以下のそれぞれの人数の場合について答えよ。ただし、いすは人数と同じ数だけある。
(1)3人のとき。
(2)4人のとき。
(3)5人のとき。
【受験算数】点Oを中心とする円がある。この円の周囲を10等分する点をA,B,C,D,E,F,G,H,I,Jとする。これらの点にさらに点Oを加えた11個の点から、3つの点をとりだし、これらを頂点とする…

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
点Oを中心とする円がある。この円の周囲を10等分する点をA,B,C,D,E,F,G,H,I,Jとする。これらの点にさらに点Oを加えた11個の点から、3つの点をとりだし、これらを頂点とする三角形を作りたい。
(1)点Oを1つの頂点とする三角形は何個できるか。
(2)直角三角形は何個できるか。
(3)三角形は全部で何個作れるか。ただし、三角形ABFのように、三角形の一辺の上に点Oを含むものも、1つの三角形として数える。
この動画を見る
点Oを中心とする円がある。この円の周囲を10等分する点をA,B,C,D,E,F,G,H,I,Jとする。これらの点にさらに点Oを加えた11個の点から、3つの点をとりだし、これらを頂点とする三角形を作りたい。
(1)点Oを1つの頂点とする三角形は何個できるか。
(2)直角三角形は何個できるか。
(3)三角形は全部で何個作れるか。ただし、三角形ABFのように、三角形の一辺の上に点Oを含むものも、1つの三角形として数える。
【受験算数】点Oを中心とする円がある。この円の周囲を6等分する点をA,B,C,D,E,Fとする。これらの点にさらに点Oを加えた7個の点から、3つの点をとりだし、これらを頂点とする三角形を作る。正三角…

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
点Oを中心とする円がある。この円の周囲を6等分する点をA,B,C,D,E,Fとする。これらの点にさらに点Oを加えた7個の点から、3つの点をとりだし、これらを頂点とする三角形を作る。
(1)正三角形は何個できるか。
(2)点Oを1つの頂点とする三角形は何個できるか。
(3)直角三角形は何個できるか。
(4)三角形は全部で何個作れるか。ただし、三角形ABDのように、三角形の一辺の上に点Oを含むものも、1つの三角形として数える。
この動画を見る
点Oを中心とする円がある。この円の周囲を6等分する点をA,B,C,D,E,Fとする。これらの点にさらに点Oを加えた7個の点から、3つの点をとりだし、これらを頂点とする三角形を作る。
(1)正三角形は何個できるか。
(2)点Oを1つの頂点とする三角形は何個できるか。
(3)直角三角形は何個できるか。
(4)三角形は全部で何個作れるか。ただし、三角形ABDのように、三角形の一辺の上に点Oを含むものも、1つの三角形として数える。
【受験算数】たて2cm、横3cmの長方形がある。その周上に10個の点A,B,C,・・・,Jがあり、となりの点と点の間の長さは1cmとする。これら10個の点から適当に3点を選び、三角形を作る。例えば…
単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
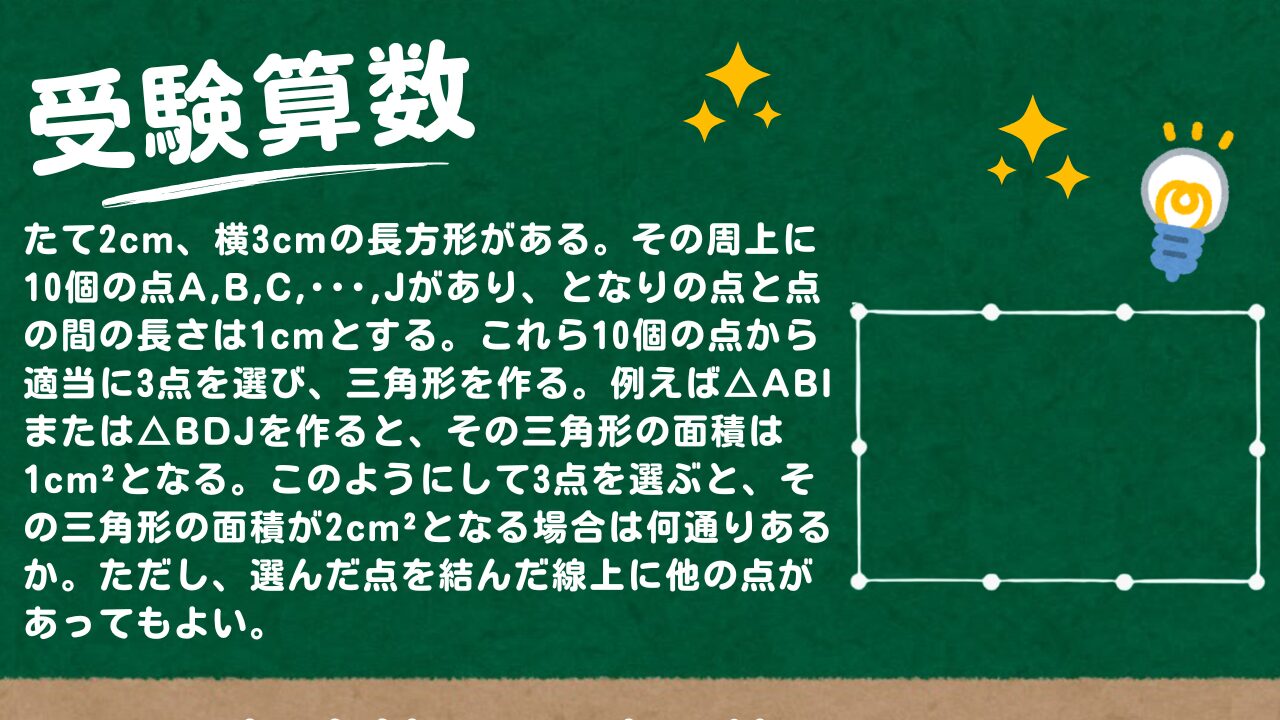
たて2cm、横3cmの長方形がある。その周上に10個の点A,B,C,・・・,Jがあり、となりの点と点の間の長さは1cmとする。これら10個の点から適当に3点を選び、三角形を作る。例えば△ABIまたは△BDJを作ると、その三角形の面積は1cm²となる。このようにして3点を選ぶと、その三角形の面積が2cm²となる場合は何通りあるか。ただし、選んだ点を結んだ線上に他の点があってもよい。
この動画を見る
たて2cm、横3cmの長方形がある。その周上に10個の点A,B,C,・・・,Jがあり、となりの点と点の間の長さは1cmとする。これら10個の点から適当に3点を選び、三角形を作る。例えば△ABIまたは△BDJを作ると、その三角形の面積は1cm²となる。このようにして3点を選ぶと、その三角形の面積が2cm²となる場合は何通りあるか。ただし、選んだ点を結んだ線上に他の点があってもよい。
【受験算数】たて2cm、横4cmの長方形がある。その周上に12個の点A,B,C,・・・,Lがあり、となりの点と点の間の長さは1cm。これら12個の点から適当に3点を選び、三角形を作る。例えば△ACE…
単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
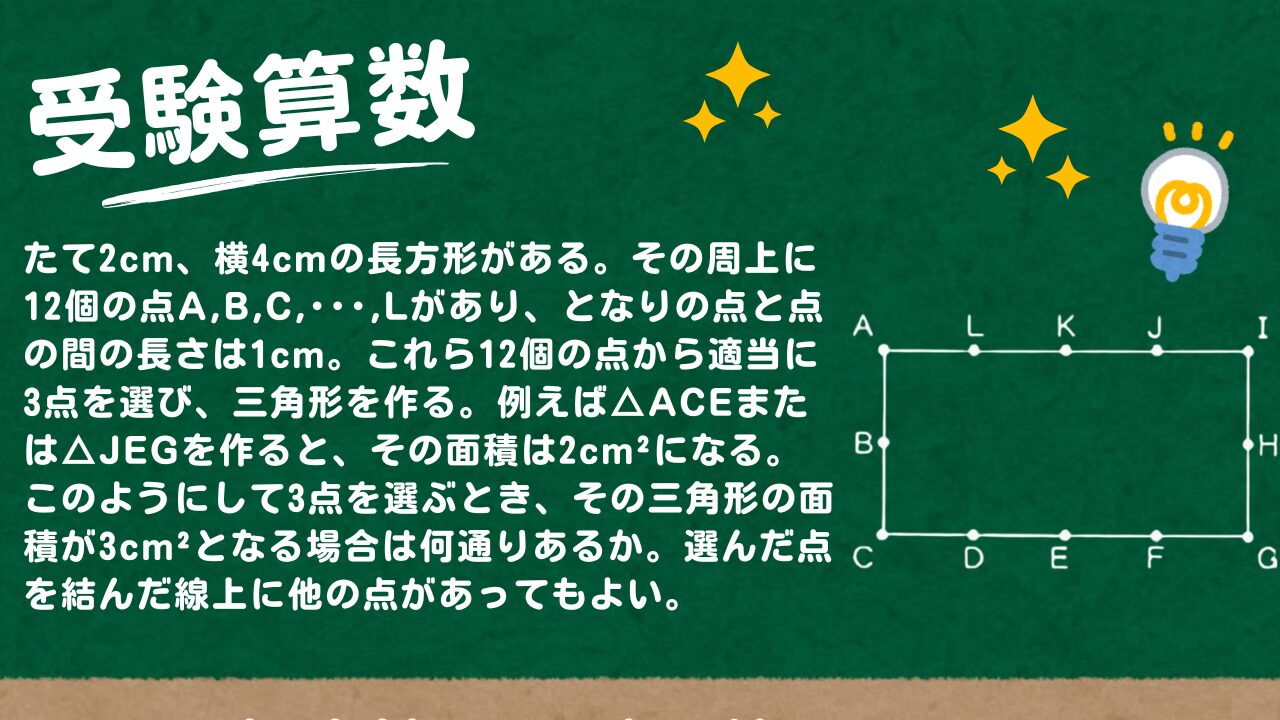
たて2cm、横4cmの長方形がある。その周上に12個の点A,B,C,・・・,Lがあり、となりの点と点の間の長さは1cm。これら12個の点から適当に3点を選び、三角形を作る。例えば△ACEまたは△JEGを作ると、その面積は2cm²になる。このようにして3点を選ぶとき、その三角形の面積が3cm²となる場合は何通りあるか。選んだ点を結んだ線上に他の点があってもよい。
この動画を見る
たて2cm、横4cmの長方形がある。その周上に12個の点A,B,C,・・・,Lがあり、となりの点と点の間の長さは1cm。これら12個の点から適当に3点を選び、三角形を作る。例えば△ACEまたは△JEGを作ると、その面積は2cm²になる。このようにして3点を選ぶとき、その三角形の面積が3cm²となる場合は何通りあるか。選んだ点を結んだ線上に他の点があってもよい。
【受験算数】右の図は一辺1cmの正方形を並べたもの。この図のなかにはいろいろな大きさの長方形がある。長方形(ただし、正方形は除く)は全部で何個あるか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図は一辺1cmの正方形を並べたもの。
(1)この図のなかにはいろいろな大きさの正方形がある。正方形は全部で何個あるか。
(2)この図のなかにはいろいろな大きさの長方形がある。長方形(ただし、正方形は除く)は全部で何個あるか。
この動画を見る
右の図は一辺1cmの正方形を並べたもの。
(1)この図のなかにはいろいろな大きさの正方形がある。正方形は全部で何個あるか。
(2)この図のなかにはいろいろな大きさの長方形がある。長方形(ただし、正方形は除く)は全部で何個あるか。
【受験算数】 右の図は一辺1cmの正方形を並べたもの。この図のなかにはいろいろな大きさの正方形がある。正方形は全部で何個あるか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図は一辺1cmの正方形を並べたもの。
(1)この図のなかにはいろいろな大きさの正方形がある。正方形は全部で何個あるか。
(2)この図のなかにはいろいろな大きさの長方形がある。長方形(ただし、正方形は除く)は全部で何個あるか。
この動画を見る
右の図は一辺1cmの正方形を並べたもの。
(1)この図のなかにはいろいろな大きさの正方形がある。正方形は全部で何個あるか。
(2)この図のなかにはいろいろな大きさの長方形がある。長方形(ただし、正方形は除く)は全部で何個あるか。
【受験算数】【赤、青、黄、緑、茶】のうちの何色かを使って、右の図のア~オの5つの部分を、となり合う部分が同じ色にならないようにぬり分けます。4色ちょうどを使うとき、色のぬり方は何通りありますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
【赤、青、黄、緑、茶】のうちの何色かを使って、右の図のア~オの5つの部分を、となり合う部分が同じ色にならないようにぬり分けます。これについて、次の問いに答えなさい。
(1) 4色ちょうどを使うとき、色のぬり方は何通りありますか。
(2) 何色使ってもよいとすると、(1)の場合もふくめて、色のぬり方は全部で何通りありますか。
この動画を見る
【赤、青、黄、緑、茶】のうちの何色かを使って、右の図のア~オの5つの部分を、となり合う部分が同じ色にならないようにぬり分けます。これについて、次の問いに答えなさい。
(1) 4色ちょうどを使うとき、色のぬり方は何通りありますか。
(2) 何色使ってもよいとすると、(1)の場合もふくめて、色のぬり方は全部で何通りありますか。
【受験算数】A, B, C. Dの4人でジャンケンを1回します。ただし、あいこでも1回と考えます。4人のグー、チョキ、パーの出し方は何通りありますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
A, B, C. Dの4人でジャンケンを1回します。ただし、あいこでも1回と考えます。これについて、次の問いに答えなさい。
(1) 4人のグー、チョキ、パーの出し方は何通りありますか。
(2) Aの出した手とBの出した手は同じで、ジャンケンの結果はあいこでした。このような4 人のグー、チョキ、パーの出し方は何通りありますか。
この動画を見る
A, B, C. Dの4人でジャンケンを1回します。ただし、あいこでも1回と考えます。これについて、次の問いに答えなさい。
(1) 4人のグー、チョキ、パーの出し方は何通りありますか。
(2) Aの出した手とBの出した手は同じで、ジャンケンの結果はあいこでした。このような4 人のグー、チョキ、パーの出し方は何通りありますか。
【受験算数】1. 2. 3. 4. 4の5枚のカードがあります。このうちの3枚をならべて3けたの整数を作ります。これについて、次の問いに答えなさい。4を2枚とも使うとき、整数は何通りできますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
1. 2. 3. 4. 4の5枚のカードがあります。このうちの3枚をならべて3けたの整数を作ります。これについて、次の問いに答えなさい。
(1) 4を2枚とも使うとき、整数は何通りできますか。
(2) (1)の場合も、ふくめて、整数は全部で何通りできますか。
(3) 奇数は何通りできますか。
この動画を見る
1. 2. 3. 4. 4の5枚のカードがあります。このうちの3枚をならべて3けたの整数を作ります。これについて、次の問いに答えなさい。
(1) 4を2枚とも使うとき、整数は何通りできますか。
(2) (1)の場合も、ふくめて、整数は全部で何通りできますか。
(3) 奇数は何通りできますか。
右の図は、同じ大きさの立方体を2つ組み合わせたものです。これらの立方体の辺(図の実線と点線)を通って、頂点Aから頂点Bまで遠回りせずに進む行き方は何通りありますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図は、同じ大きさの立方体を2つ組み合わせたものです。これらの立方体の辺(図の実線と点線)を通って、頂点Aから頂点Bまで遠回りせずに進む行き方は何通りありますか。
この動画を見る
右の図は、同じ大きさの立方体を2つ組み合わせたものです。これらの立方体の辺(図の実線と点線)を通って、頂点Aから頂点Bまで遠回りせずに進む行き方は何通りありますか。
【受験算数】(1) A町からD町まで行く方法は何通りありますか。(2) A町からD町まで行く方法のうち、バスを1回だけ使う方法は何通りありますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1) A町からD町まで行く方法は何通りありますか。
(2) A町からD町まで行く方法のうち、バスを1回だけ使う方法は何通りありますか。
この動画を見る
(1) A町からD町まで行く方法は何通りありますか。
(2) A町からD町まで行く方法のうち、バスを1回だけ使う方法は何通りありますか。
【受験算数】A, B, Cの3人の男子と、D、Eの2人の女子がいます。この5人でリレーの順番を決めます。男女が交互になるようなリレーの順番は何通りありますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
A, B, Cの3人の男子と、D、Eの2人の女子がいます。この5人でリレーの順番を決めます。これについて、次の問いに答えなさい。
(1) 男女が交互になるようなリレーの順番は何通りありますか。
(2) 2人の女子が続けて走るようなリレーの順番は何通りありますか。
この動画を見る
A, B, Cの3人の男子と、D、Eの2人の女子がいます。この5人でリレーの順番を決めます。これについて、次の問いに答えなさい。
(1) 男女が交互になるようなリレーの順番は何通りありますか。
(2) 2人の女子が続けて走るようなリレーの順番は何通りありますか。
【受験算数】下の図を、赤、青、黄、緑の4色でぬり分ける方法は何通りありますか。ただし、 使わない色があってもかまいません。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の図を、赤、青、黄、緑の4色でぬり分ける方法は何通りありますか。ただし、 使わない色があってもかまいません。
この動画を見る
下の図を、赤、青、黄、緑の4色でぬり分ける方法は何通りありますか。ただし、 使わない色があってもかまいません。
【受験算数】右の図を、赤、青、黄、緑、紫の5色でぬり分けることにします。(1) 異なる4色を用いてぬり分ける方法は何通りありますか。(2) 異なる3色を用いてぬり分ける方法は何通りありますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図を、赤、青、黄、緑、紫の5色でぬり分けることにします。
(1) 異なる4色を用いてぬり分ける方法は何通りありますか。
(2) 異なる3色を用いてぬり分ける方法は何通りありますか。
(3) ぬり分ける方法は全部で何通りありますか
この動画を見る
右の図を、赤、青、黄、緑、紫の5色でぬり分けることにします。
(1) 異なる4色を用いてぬり分ける方法は何通りありますか。
(2) 異なる3色を用いてぬり分ける方法は何通りありますか。
(3) ぬり分ける方法は全部で何通りありますか
【受験算数】下の図を、赤、青、黄の3色でぬり分ける方法は何通りありますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の図を、赤、青、黄の3色でぬり分ける方法は何通りありますか。
この動画を見る
下の図を、赤、青、黄の3色でぬり分ける方法は何通りありますか。
【受験算数】右の図を、赤、青、黄、緑の4色でぬり分けることにします。(1) 異なる3色を用いてぬり分ける方法は何通りありますか。(2) 異なる2色を用いてぬり分ける方法は何通りありますか。
単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
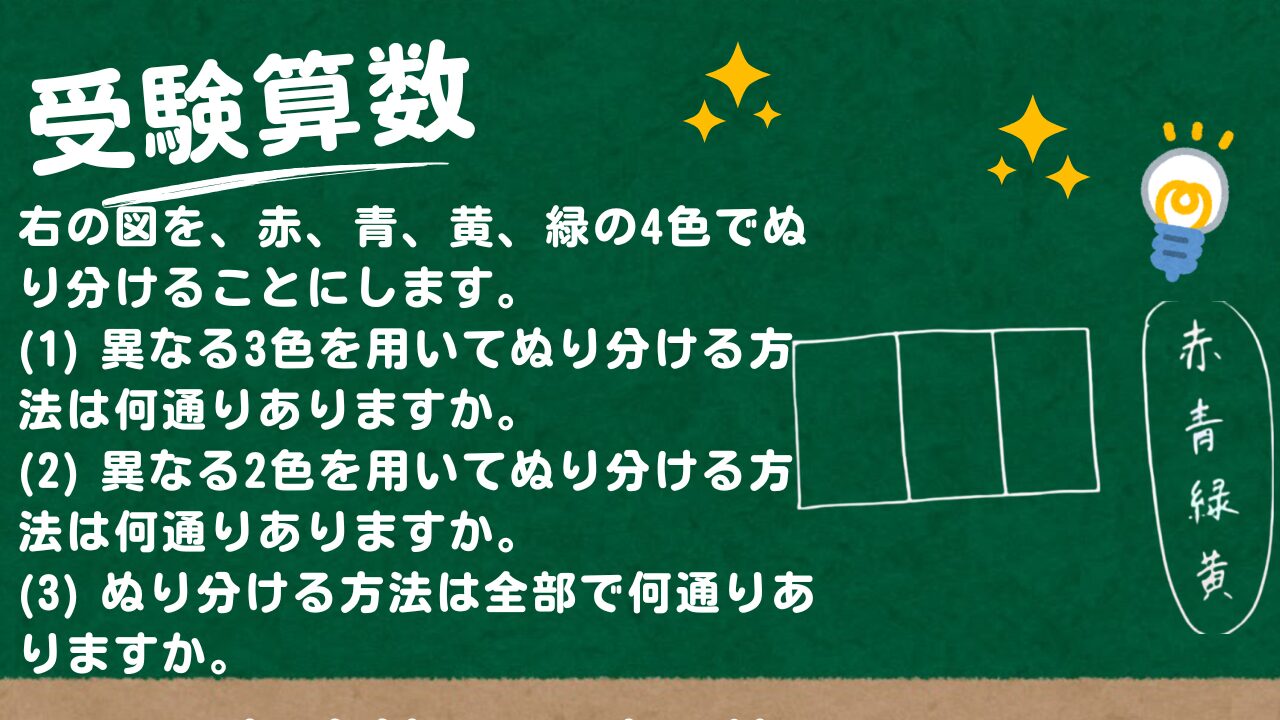
右の図を、赤、青、黄、緑の4色でぬり分けることにします。
(1) 異なる3色を用いてぬり分ける方法は何通りありますか。
(2) 異なる2色を用いてぬり分ける方法は何通りありますか。
(3) ぬり分ける方法は全部で何通りありますか。
この動画を見る
右の図を、赤、青、黄、緑の4色でぬり分けることにします。
(1) 異なる3色を用いてぬり分ける方法は何通りありますか。
(2) 異なる2色を用いてぬり分ける方法は何通りありますか。
(3) ぬり分ける方法は全部で何通りありますか。
【受験算数】下図のような道路があります。道路は右、上、右上の3方向に進むことができます。Aが通行止めになりました。このとき、PからQまで行く道順は何通りありますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下図のような道路があります。道路は右、上、右上の3方向に進むことができます。
(1) PからQまで行く道順は全部で何通りありますか。
(2) Aが通行止めになりました。このとき、PからQまで行く道順は何通りありますか。
この動画を見る
下図のような道路があります。道路は右、上、右上の3方向に進むことができます。
(1) PからQまで行く道順は全部で何通りありますか。
(2) Aが通行止めになりました。このとき、PからQまで行く道順は何通りありますか。
【受験算数】下図のような道路があります。PからQまで行く最短の道順を考えます。(1) 全部で何通りありますか。(2) PからAを通ってQまで行く道順は何通りありますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下図のような道路があります。PからQまで行く最短の道順を考えます。
(1) 全部で何通りありますか。
(2) PからAを通ってQまで行く道順は何通りありますか。
(3) AとBの間が通行止めになりました。このとき、PからQまで行く道順は何通りありますか。
この動画を見る
下図のような道路があります。PからQまで行く最短の道順を考えます。
(1) 全部で何通りありますか。
(2) PからAを通ってQまで行く道順は何通りありますか。
(3) AとBの間が通行止めになりました。このとき、PからQまで行く道順は何通りありますか。
【受験算数】A町,B町,C町の3つの町が、下図のようにいくつかの道で結ばれています。A町からC町に行く道順は何通りありますか。ただし、同じ町を2回以上通ることはできません。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
A町,B町,C町の3つの町が、下図のようにいくつかの道で結ばれています。
A町からC町に行く道順は何通りありますか。ただし、同じ町を2回以上通ることはできません。
この動画を見る
A町,B町,C町の3つの町が、下図のようにいくつかの道で結ばれています。
A町からC町に行く道順は何通りありますか。ただし、同じ町を2回以上通ることはできません。
【受験算数】A町、B町、C町の3つの町が、下図のようにいくつかの道で結ばれています。A町からB町を通ってC町に行く道順は何通りありますか。
単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
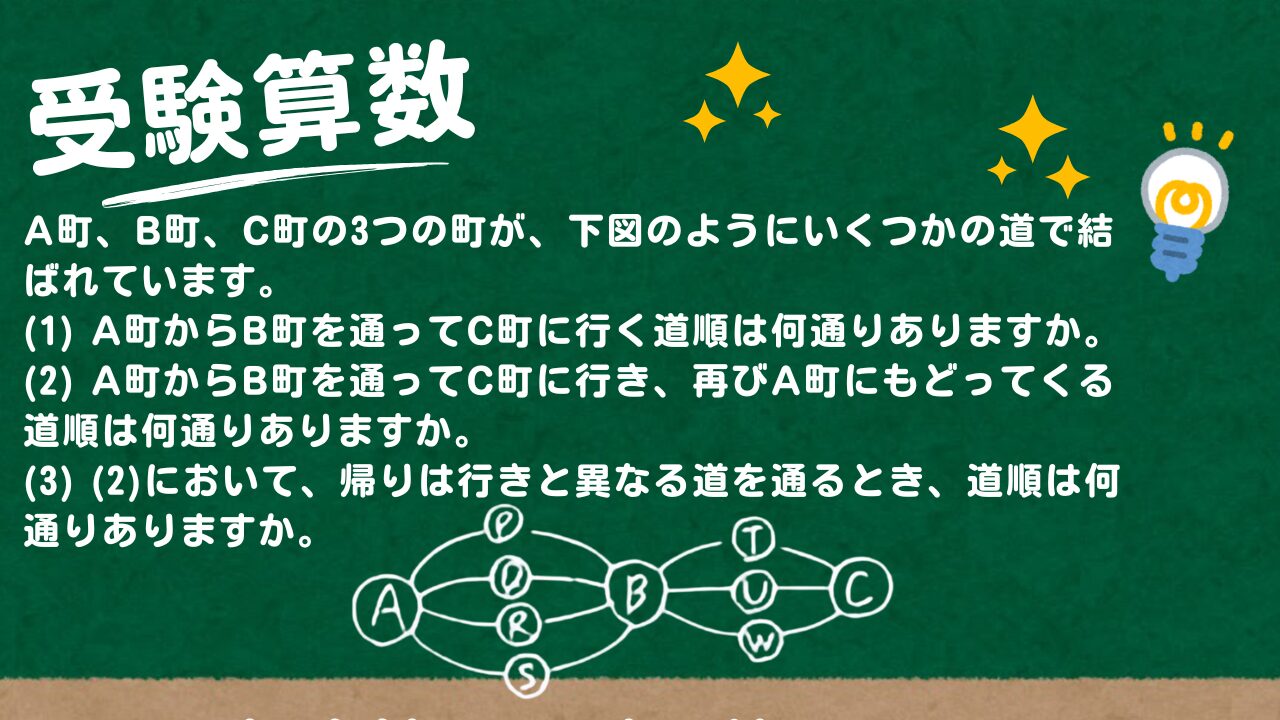
A町、B町、C町の3つの町が、下図のようにいくつかの道で結ばれています。
(1) A町からB町を通ってC町に行く道順は何通りありますか。
(2) A町からB町を通ってC町に行き、再びA町にもどってくる道順は何通りありますか。
(3) (2)において、帰りは行きと異なる道を通るとき、道順は何通りありますか。
この動画を見る
A町、B町、C町の3つの町が、下図のようにいくつかの道で結ばれています。
(1) A町からB町を通ってC町に行く道順は何通りありますか。
(2) A町からB町を通ってC町に行き、再びA町にもどってくる道順は何通りありますか。
(3) (2)において、帰りは行きと異なる道を通るとき、道順は何通りありますか。
ちがう、ちがう!そうじゃ、そうじゃな〜い!!じゃない方を数えた方が速いんだよ! 2025年広尾学園中

