算数(中学受験)
算数(中学受験)
 算数(中学受験)
算数(中学受験)
こんなの解けるわけなくない!?算数オリンピックの難問!【中学受験算数】
単元:
#算数(中学受験)#数学検定・数学甲子園・数学オリンピック等#平面図形#角度と面積#平面図形その他#数学オリンピック
指導講師:
こばちゃん塾
問題文全文(内容文):
三角形ABEと四角形BCDEの面積比は?
*図は動画内参照
この動画を見る
三角形ABEと四角形BCDEの面積比は?
*図は動画内参照
2024年洗足学園中算数大問①②中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#平面図形#相似と相似を利用した問題#場合の数#場合の数#洗足学園中学
指導講師:
重吉
問題文全文(内容文):
(1) 次の計算をしなさい。
(23-0.5) × (2.8+3×5+1) + 3.14
(2) ▭にあてはまる数を答えなさい。
0.84 x (0.75-1 28 + ▭×9+14+(1.02-) = 76
2
次の問いに答えなさい。
(1) Aさんが買い物をしました。最初の店では所持金の今より200円多く使い。 2番目の店では残った所持金の方よりも400円多く使いました。3番目の店で残った所持金の一よりも600円多く使ったところ、所持金をすべて使いきりました。Aさんは、はじめに何円持っていましたか。
(2) 1. 2. 3. 4.5.6.7が1つずつ書いてある7枚のカードから4枚を選び、2枚ずつ並べて2桁の奇数を2つ作ります。大きい方の数が小さい方の数の倍数になるとき、考えることができる奇数の組をすべて求めなさい。なお、答えは(13.25) のように書きなさい。
(3) 高さが同じで底面積が異なる直方体の形をした2つの容器A.Bがあります。 この2つの容器に空の状態から毎分1Lの割合で同時に水を入れ、容器Aの高さの半分まで水を入れたところで、容器Aについている毎分200mLの水を排出する排水口を開けました。その後、容器AとBが同時に満水になりました。 このとき、容器AとBの底面積の比をもっとも簡単な整数で答えなさい。
(4)四角形ABCDは長方形です。 直線BEと直線FDが平行のとき、 三角形ABGと三角形FDHの面積の比をもっとも簡単な整数で答えなさい。 (図は動画内参照)
この動画を見る
(1) 次の計算をしなさい。
(23-0.5) × (2.8+3×5+1) + 3.14
(2) ▭にあてはまる数を答えなさい。
0.84 x (0.75-1 28 + ▭×9+14+(1.02-) = 76
2
次の問いに答えなさい。
(1) Aさんが買い物をしました。最初の店では所持金の今より200円多く使い。 2番目の店では残った所持金の方よりも400円多く使いました。3番目の店で残った所持金の一よりも600円多く使ったところ、所持金をすべて使いきりました。Aさんは、はじめに何円持っていましたか。
(2) 1. 2. 3. 4.5.6.7が1つずつ書いてある7枚のカードから4枚を選び、2枚ずつ並べて2桁の奇数を2つ作ります。大きい方の数が小さい方の数の倍数になるとき、考えることができる奇数の組をすべて求めなさい。なお、答えは(13.25) のように書きなさい。
(3) 高さが同じで底面積が異なる直方体の形をした2つの容器A.Bがあります。 この2つの容器に空の状態から毎分1Lの割合で同時に水を入れ、容器Aの高さの半分まで水を入れたところで、容器Aについている毎分200mLの水を排出する排水口を開けました。その後、容器AとBが同時に満水になりました。 このとき、容器AとBの底面積の比をもっとも簡単な整数で答えなさい。
(4)四角形ABCDは長方形です。 直線BEと直線FDが平行のとき、 三角形ABGと三角形FDHの面積の比をもっとも簡単な整数で答えなさい。 (図は動画内参照)
【小6算数手元解説】受験算数 2つずつの和① 【問題文は概要欄】

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
理数個別チャンネル
問題文全文(内容文):
異なる4つの整数A、B、C、Dがあります。小さい方からA. B. C. Dの順 になっています。この4つから2つずつ取り出してその和を作ったら、25, 27, 31, 32, 36, 38の6通りになりました。次の問いに答えなさい。
(1) A+Dはいくらですか。
(2) Dはいくらですか。
この動画を見る
異なる4つの整数A、B、C、Dがあります。小さい方からA. B. C. Dの順 になっています。この4つから2つずつ取り出してその和を作ったら、25, 27, 31, 32, 36, 38の6通りになりました。次の問いに答えなさい。
(1) A+Dはいくらですか。
(2) Dはいくらですか。
【受験算数】速さに関する問題(C4):途中で出会う

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材#5年算数W-支援
指導講師:
受験算数の森
問題文全文(内容文):
大川君はA地からB地に向かって、小山君はB地からA地に向かって、同時に歩き始めました。2人は歩き始めてから28分後にP地点で出会いました。大川君は出会ってから20分後にB地に着きました。そのとき、小山君はA地の手前960mのところを歩いていました。
(1)大川君と小山君の速さの比は何対何ですか。
(2)A地とB地は何m離れていますか。
(3)P地点はA地から何mのところですか。
この動画を見る
大川君はA地からB地に向かって、小山君はB地からA地に向かって、同時に歩き始めました。2人は歩き始めてから28分後にP地点で出会いました。大川君は出会ってから20分後にB地に着きました。そのとき、小山君はA地の手前960mのところを歩いていました。
(1)大川君と小山君の速さの比は何対何ですか。
(2)A地とB地は何m離れていますか。
(3)P地点はA地から何mのところですか。
2024年筑波大附属中算数大問①(5)~(7)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
重吉
問題文全文(内容文):
問題文
(5)縦の長さが200mm、横の長さが300mmの用紙がある、その重さは36gです。
この用紙1m²の重さは何gですか。
(6)下の図のように、半径3cmの円を規則的にならべて、そのまわりの長さがもっとも短くなるように囲んだ図形を考えます。図形の周りの長さ(図の太線部分)が初めて5mより大きくなるのは、何番目の図形ですか。ただし、円周率は3.14とします。
(7)1から1000mでの整数のうち、数字の4を使っていない整数は全部でいくつありますか。
この動画を見る
問題文
(5)縦の長さが200mm、横の長さが300mmの用紙がある、その重さは36gです。
この用紙1m²の重さは何gですか。
(6)下の図のように、半径3cmの円を規則的にならべて、そのまわりの長さがもっとも短くなるように囲んだ図形を考えます。図形の周りの長さ(図の太線部分)が初めて5mより大きくなるのは、何番目の図形ですか。ただし、円周率は3.14とします。
(7)1から1000mでの整数のうち、数字の4を使っていない整数は全部でいくつありますか。
【中学受験問題に挑戦】130(”大人”は頭の体操) 直角三角形と半円の考察
単元:
#算数(中学受験)#平面図形#図形の移動
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
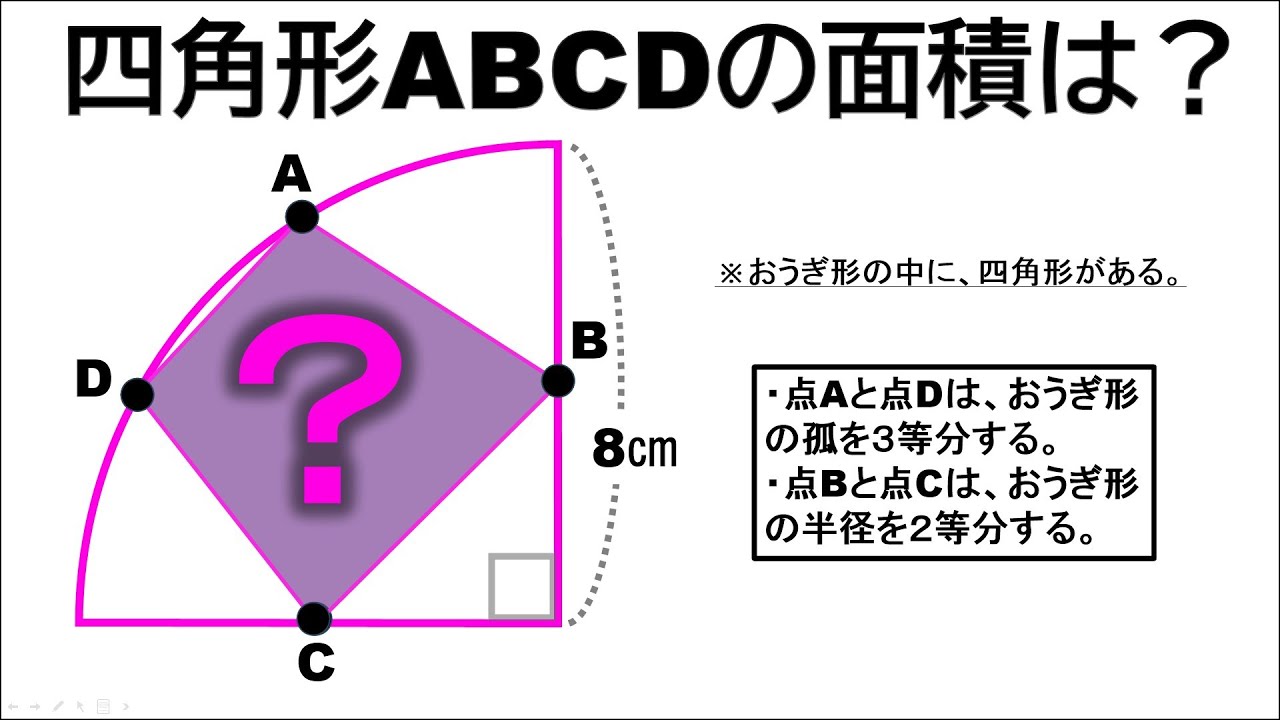
おうぎ形の中に四角形がある。
点Aと点Dは、おうぎ形の弧を3等分する。
点Bと点Cは、おうぎ形の半径を2等分する。
*図は動画内参照
四角形ABCD面積は?
この動画を見る
おうぎ形の中に四角形がある。
点Aと点Dは、おうぎ形の弧を3等分する。
点Bと点Cは、おうぎ形の半径を2等分する。
*図は動画内参照
四角形ABCD面積は?
2024年筑波大附属中算数大問①(5)~(7)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#文章題#単位・比と割合・比例・反比例#筑波大学附属中学
指導講師:
重吉
問題文全文(内容文):
(5) 縦の長さが200mm、横の長さが300mmの用紙があり、その重さは3.6gです。
この用紙1m²の重さは何gですか。
(6) 下の図のように、半径3cmの円を規則的にならべて、そのまわりの長さがもっとも短くなるように囲んだ図形を考えます。図形のまわりの長さ(図の太線部分)が初めて 5mより大きくなるのは、何番目の図形ですか。ただし、円周率は3.14とします。
※図は動画内参照
(7) 1から1000までの整数のうち、数字の4を使っていない整数は全部でいくつありますか。
この動画を見る
(5) 縦の長さが200mm、横の長さが300mmの用紙があり、その重さは3.6gです。
この用紙1m²の重さは何gですか。
(6) 下の図のように、半径3cmの円を規則的にならべて、そのまわりの長さがもっとも短くなるように囲んだ図形を考えます。図形のまわりの長さ(図の太線部分)が初めて 5mより大きくなるのは、何番目の図形ですか。ただし、円周率は3.14とします。
※図は動画内参照
(7) 1から1000までの整数のうち、数字の4を使っていない整数は全部でいくつありますか。
【受験算数】速さに関する問題(C3):バス停まで歩く

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材#5年算数W-支援
指導講師:
受験算数の森
問題文全文(内容文):
太郎くんは家からバス停まで歩き、7分待ったあとバスに乗って駅に着きました。家を出てから駅に着くまでにかかった時間は23分でした。帰りは駅から行きと同じ道を歩いて65分で家に着きました。バスの速さは分速550m、歩く速さは時速3.6kmとします。
(1)家から駅までの道のりは何mですか。
(2)家からバス停までの道のりは何mですか。
この動画を見る
太郎くんは家からバス停まで歩き、7分待ったあとバスに乗って駅に着きました。家を出てから駅に着くまでにかかった時間は23分でした。帰りは駅から行きと同じ道を歩いて65分で家に着きました。バスの速さは分速550m、歩く速さは時速3.6kmとします。
(1)家から駅までの道のりは何mですか。
(2)家からバス停までの道のりは何mですか。
【受験算数】速さに関する問題(C2):ちょうど着くには
単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材#5年算数W-支援
指導講師:
受験算数の森
問題文全文(内容文):
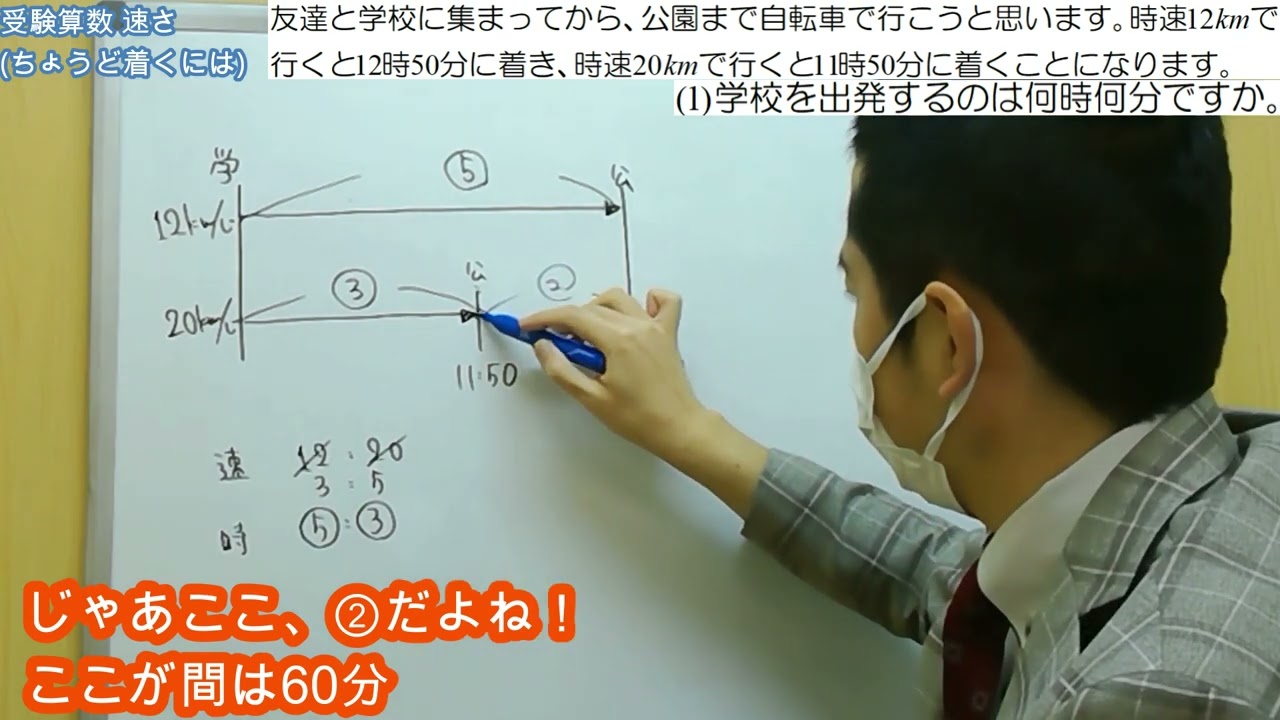
友達と学校に集まってから、公園まで自転車で行こうと思います。時速12kmで行くと12時50分に着き、時速20kmで行くと11時50分に着くことになります。
(1)学校を出発するのは何時何分ですか。
(2)学校から公園までの距離は何kmですか。
(3)ちょうど12時に着くようにするには、時速何kmで行けばよいですか。
この動画を見る
友達と学校に集まってから、公園まで自転車で行こうと思います。時速12kmで行くと12時50分に着き、時速20kmで行くと11時50分に着くことになります。
(1)学校を出発するのは何時何分ですか。
(2)学校から公園までの距離は何kmですか。
(3)ちょうど12時に着くようにするには、時速何kmで行けばよいですか。
2024年筑波大学附属中算数大問①(1)~(4)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#平面図形#角度と面積#筑波大学附属中学
指導講師:
重吉
問題文全文(内容文):
(1) 4 (3/ 16) +13/16 ÷ 3(1/4) -3を計算しなさい。
(2) 整数Aを5でわり、その商の小数第一位を四捨五入すると27になります。また、整数Aを8でわり、その商の小数第一位を切り捨てると16になります。このとき、Aにあてはまる整数は全部でいくつありますか。
(3) えんぴつ 136本、消しゴム 187個、ノート343冊があります。これらを何人かの子どもにそれぞれ同じ数ずつ分けると、えんぴつは8本不足し、消しゴムは7個あまり、 ノートは19冊あまりました。分けるときは、子どもの人数よりも多くあまりがでないように分けています。このとき、子どもの人数は何人ですか。
(4) 下の図(動画内参照)は、正方形ABCDの紙をAEを折り目として折ったものです。直線BDとBC によってできる角の大きさが12のとき、図の⑦の角度を求めなさい。
この動画を見る
(1) 4 (3/ 16) +13/16 ÷ 3(1/4) -3を計算しなさい。
(2) 整数Aを5でわり、その商の小数第一位を四捨五入すると27になります。また、整数Aを8でわり、その商の小数第一位を切り捨てると16になります。このとき、Aにあてはまる整数は全部でいくつありますか。
(3) えんぴつ 136本、消しゴム 187個、ノート343冊があります。これらを何人かの子どもにそれぞれ同じ数ずつ分けると、えんぴつは8本不足し、消しゴムは7個あまり、 ノートは19冊あまりました。分けるときは、子どもの人数よりも多くあまりがでないように分けています。このとき、子どもの人数は何人ですか。
(4) 下の図(動画内参照)は、正方形ABCDの紙をAEを折り目として折ったものです。直線BDとBC によってできる角の大きさが12のとき、図の⑦の角度を求めなさい。
2024年筑波大学附属中算数大問①(1)~(4)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数の性質その他#約数・倍数を利用する問題#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#筑波大学附属中学
指導講師:
重吉
問題文全文(内容文):
(1)
$4\dfrac{3}{16}\div\dfrac{13}{16}\div3\dfrac{1}{4}-3$を計算しなさい。
(2)
整数Aを5で割り、その商の小数第一位を四捨五入すると27になります。また、整数Aを8で割り、その商の小数第一位を切り捨てると16になります。このとき、Aに当てはまる整数は全部でいくつありますか。
(3)
えんぴつ136本、消しゴム187個、ノート343冊があります。これらを何人かの子どもにそれぞれ同じ数分けると、えんぴつは8本不足し、消しゴムは7個あまり、ノートは19冊あまりました。分けるときは、子どもの人数よりも多く余りが出ないように分けています。このとき子どもの人数は何人ですか。
(4)
下の図は、正方形ABCDの紙をAEを折り目として折ったものです。直線BDとBCによってできる角の大きさが12°のとき、図の㋐の角度を求めなさい。
この動画を見る
(1)
$4\dfrac{3}{16}\div\dfrac{13}{16}\div3\dfrac{1}{4}-3$を計算しなさい。
(2)
整数Aを5で割り、その商の小数第一位を四捨五入すると27になります。また、整数Aを8で割り、その商の小数第一位を切り捨てると16になります。このとき、Aに当てはまる整数は全部でいくつありますか。
(3)
えんぴつ136本、消しゴム187個、ノート343冊があります。これらを何人かの子どもにそれぞれ同じ数分けると、えんぴつは8本不足し、消しゴムは7個あまり、ノートは19冊あまりました。分けるときは、子どもの人数よりも多く余りが出ないように分けています。このとき子どもの人数は何人ですか。
(4)
下の図は、正方形ABCDの紙をAEを折り目として折ったものです。直線BDとBCによってできる角の大きさが12°のとき、図の㋐の角度を求めなさい。
【小6算数手元解説】平均算(面積図)何冊買ったら平均70円?【問題文は概要欄】

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
理数個別チャンネル
問題文全文(内容文):
A,B,C,D,E,F 6人の平均点よりC,D,E,F 4人の平均点の方が4点高く、AとBの点数の和は150点です。このとき、6人の平均点は何点ですか。
ノートをまとめて買うことになりました。代金は20冊で1800円、21冊目から50冊目までは1冊80円、51冊目からは1冊60円です。次の問いに答えなさい。
(1)80冊買うと1冊平均何円になりますか。
(2)何冊買うと1冊平均70円になりますか。
この動画を見る
A,B,C,D,E,F 6人の平均点よりC,D,E,F 4人の平均点の方が4点高く、AとBの点数の和は150点です。このとき、6人の平均点は何点ですか。
ノートをまとめて買うことになりました。代金は20冊で1800円、21冊目から50冊目までは1冊80円、51冊目からは1冊60円です。次の問いに答えなさい。
(1)80冊買うと1冊平均何円になりますか。
(2)何冊買うと1冊平均70円になりますか。
【算数練習】115(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#相似と相似を利用した問題
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
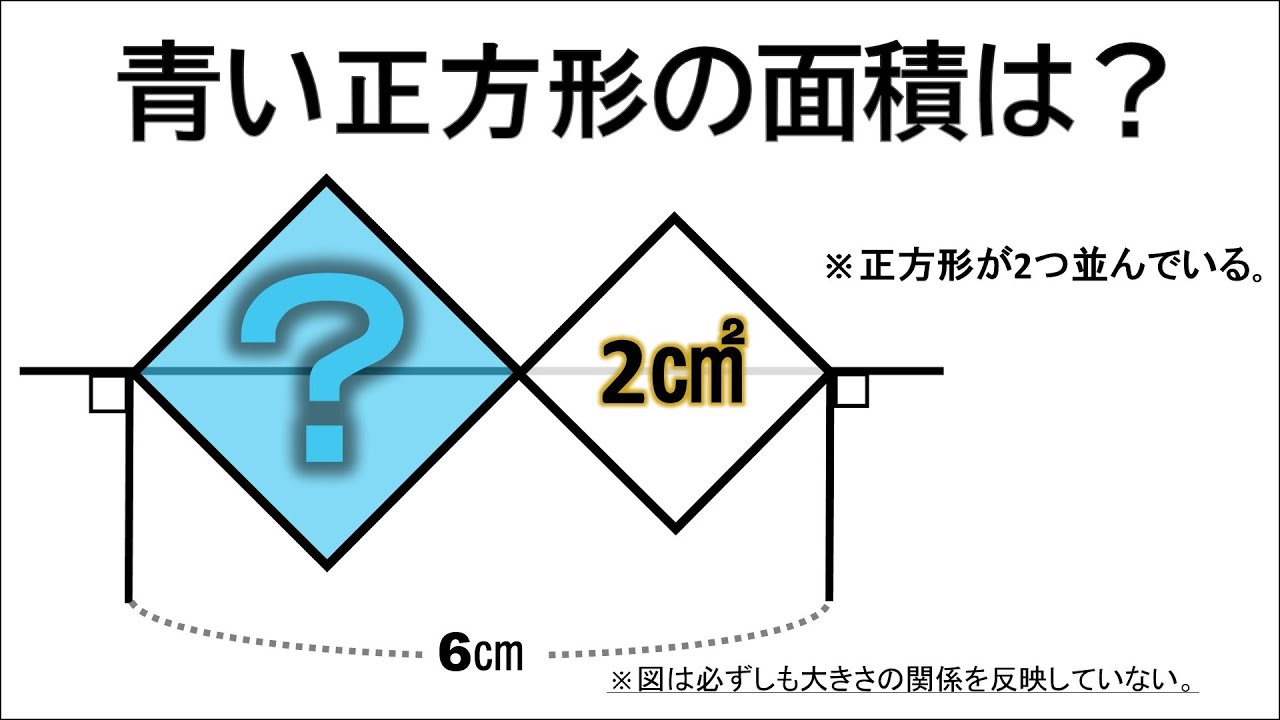
正方形が2つ並んでいる。
*図は動画内参照
青い正方形の面積は?
この動画を見る
正方形が2つ並んでいる。
*図は動画内参照
青い正方形の面積は?
2024年女子学院中算数大問①(1)~(5)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#文章題#平均算・過不足算・差集め算・消去算#平面図形#角度と面積#相似と相似を利用した問題#女子学院中学
指導講師:
重吉
問題文全文(内容文):
※図は動画内参照
(1)
$\Box$に当てはまる数を入れなさい。
$18.7+\{ 13.4\times(\dfrac{1}{20}+\Box)-2\dfrac{1}{3} \}\div2\dfrac{6}{11}=20.24$
(2)
図のように、円周を10等分する点を取りました。点Oは円の中心、三角形ABCは正三角形です。
角アは$\Box$度、角イは$\Box$度、角ウは$\Box$度
(3)
図のように、長方形の紙を対角線を折り目としておりました。
斜線部分の面積は$\Box$㎠です。
(4)
図のように、棒を使って正三角形と正方形を作ります。
➀100個目の正方形を作り終えたとき、使った棒は$\Box$本です。
②棒が1000本ある時、正三角形は$\Box$個、正方形は$\Box$個まで作ることができます。
(5)
クラスの生徒に消しゴムを配ります。全員に10個ずつ配ると32個足りないので、先生と勝敗がつくまでじゃんけんをして、勝った人には11個、負けた人には7個配ることにしました。勝った人は負けた人よりも5人少なかったので、消しゴムは9個あまりました。
クラスの人数は$\Box$人、消しゴムは全部で$\Box$個です。
この動画を見る
※図は動画内参照
(1)
$\Box$に当てはまる数を入れなさい。
$18.7+\{ 13.4\times(\dfrac{1}{20}+\Box)-2\dfrac{1}{3} \}\div2\dfrac{6}{11}=20.24$
(2)
図のように、円周を10等分する点を取りました。点Oは円の中心、三角形ABCは正三角形です。
角アは$\Box$度、角イは$\Box$度、角ウは$\Box$度
(3)
図のように、長方形の紙を対角線を折り目としておりました。
斜線部分の面積は$\Box$㎠です。
(4)
図のように、棒を使って正三角形と正方形を作ります。
➀100個目の正方形を作り終えたとき、使った棒は$\Box$本です。
②棒が1000本ある時、正三角形は$\Box$個、正方形は$\Box$個まで作ることができます。
(5)
クラスの生徒に消しゴムを配ります。全員に10個ずつ配ると32個足りないので、先生と勝敗がつくまでじゃんけんをして、勝った人には11個、負けた人には7個配ることにしました。勝った人は負けた人よりも5人少なかったので、消しゴムは9個あまりました。
クラスの人数は$\Box$人、消しゴムは全部で$\Box$個です。
2024年女子学院中算数大問①(1)~(5)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#文章題#平均算・過不足算・差集め算・消去算#平面図形#角度と面積#相似と相似を利用した問題#女子学院中学
指導講師:
重吉
問題文全文(内容文):
1. にあてはまる数を入れなさい。
(1)18.7+ {13.4× (1/20 +▭) -2(1/3)} ÷2(6/11) =20.24
(2)図(動画内参照)のように、円周を10等分する点をとりました。
点0は円の中心、三角形ABCは正三角形です。
角㋐▭度、角㋑▭度、角㋒▭度
(3) 図(動画内参照)のように、長方形の紙を対角線を折り目として折りました。
斜線部の部分の面積は▭cm²です。
(4) 図(動画内参照)のように、棒を使って正三角形と正方形を作ります。
① 100個目の正方形を作り終えたとき、使った棒は▭本です。
② 棒が1000本あるとき、正三角形は▭個,正方形は▭個まで作ることができます。
(5) クラスの生徒に消しゴムを配ります。全員に10個ずつ配ると32個足りないので、先生と勝敗がつくまでじゃんけんをして、勝った人には11個、負けた人には7個配ることにしました。勝った人は負けた人よりも5人少なかったので、 消しゴムは9個余りました。 I
クラスの人数は▭人,消しゴムは全部で▭個です。
この動画を見る
1. にあてはまる数を入れなさい。
(1)18.7+ {13.4× (1/20 +▭) -2(1/3)} ÷2(6/11) =20.24
(2)図(動画内参照)のように、円周を10等分する点をとりました。
点0は円の中心、三角形ABCは正三角形です。
角㋐▭度、角㋑▭度、角㋒▭度
(3) 図(動画内参照)のように、長方形の紙を対角線を折り目として折りました。
斜線部の部分の面積は▭cm²です。
(4) 図(動画内参照)のように、棒を使って正三角形と正方形を作ります。
① 100個目の正方形を作り終えたとき、使った棒は▭本です。
② 棒が1000本あるとき、正三角形は▭個,正方形は▭個まで作ることができます。
(5) クラスの生徒に消しゴムを配ります。全員に10個ずつ配ると32個足りないので、先生と勝敗がつくまでじゃんけんをして、勝った人には11個、負けた人には7個配ることにしました。勝った人は負けた人よりも5人少なかったので、 消しゴムは9個余りました。 I
クラスの人数は▭人,消しゴムは全部で▭個です。
すぐ解ける灘中学校のシンプル難問!○○に気づけば本当に楽勝!?【中学受験算数】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#平面図形その他#灘中学校
指導講師:
こばちゃん塾
問題文全文(内容文):
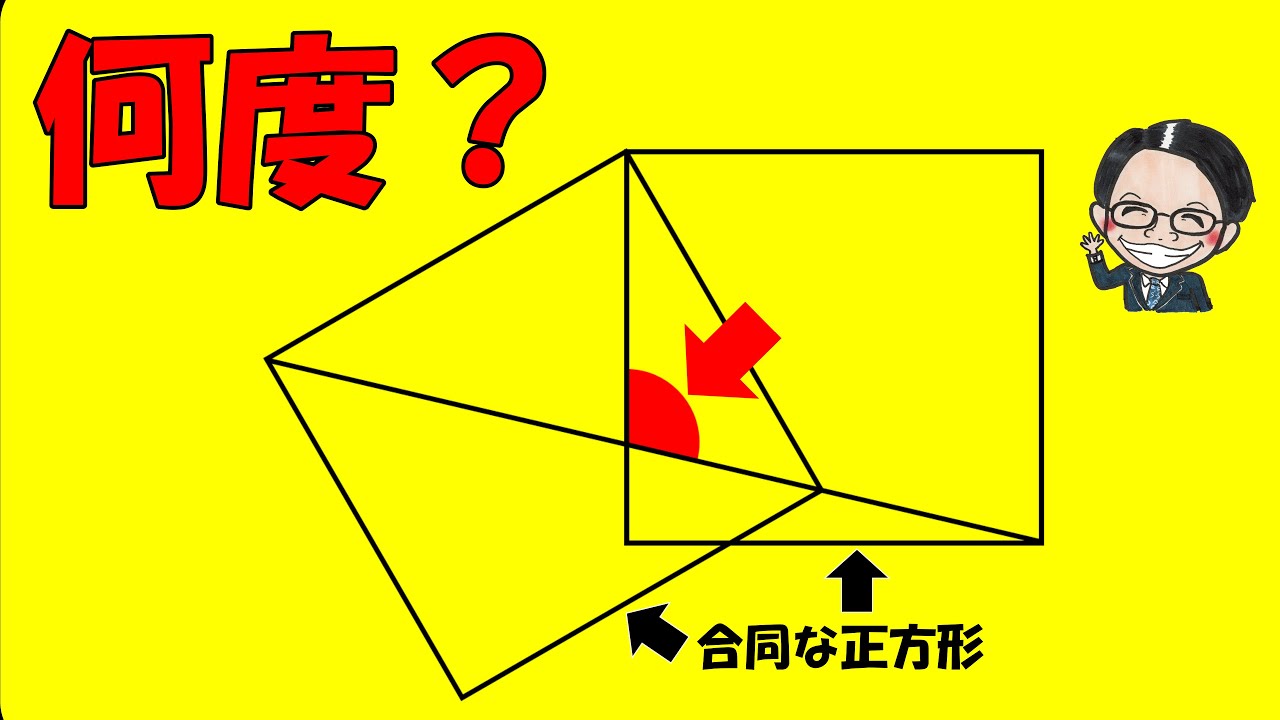
正方形ABCDと正方形DEFGは合同です。
下図でxは何度?
*図は動画内参照
2001年 灘中学校
この動画を見る
正方形ABCDと正方形DEFGは合同です。
下図でxは何度?
*図は動画内参照
2001年 灘中学校
生まれてから鼻水集めると何リットル?

2024年早稲田中算数大問①(1)~(3)ちゅがく受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#文章題#単位・比と割合・比例・反比例#場合の数#場合の数#早稲田中学
指導講師:
重吉
問題文全文(内容文):
(1) 次の計算をし、約分できない分数で答えなさい。
5 / (2×3) + 11 / (3×4) + 19 / (4×5) + 29 / (5×6)
(2) 次郎くんはある本を読み始めて最初の5日間は同じページ数を読み進め、そのあとの3日間は旅行中のため1日あたり6ページ減らして読みました。旅行から帰ったあとは毎日、旅行中の1日あたりの4倍のページ数を読んだところ、旅行から帰って4日目にはじめて200ページを超え、この日にちょうどこの本を読み終えました。この本は全部で何ページありますか。
(3) 下の図(動画内参照)のような東西に4本、南北に6本の道があります。南スタート地点から東ゴール、西ゴール、北ゴール地点のいずれかに進む方法は全部で何通りありますか。ただし、南方向には進むことができませんが、北方向、東方向,西方向のいずれかに進むことができます。また、一度通った道を通ることはできませんが、 遠回りすることはできます。
この動画を見る
(1) 次の計算をし、約分できない分数で答えなさい。
5 / (2×3) + 11 / (3×4) + 19 / (4×5) + 29 / (5×6)
(2) 次郎くんはある本を読み始めて最初の5日間は同じページ数を読み進め、そのあとの3日間は旅行中のため1日あたり6ページ減らして読みました。旅行から帰ったあとは毎日、旅行中の1日あたりの4倍のページ数を読んだところ、旅行から帰って4日目にはじめて200ページを超え、この日にちょうどこの本を読み終えました。この本は全部で何ページありますか。
(3) 下の図(動画内参照)のような東西に4本、南北に6本の道があります。南スタート地点から東ゴール、西ゴール、北ゴール地点のいずれかに進む方法は全部で何通りありますか。ただし、南方向には進むことができませんが、北方向、東方向,西方向のいずれかに進むことができます。また、一度通った道を通ることはできませんが、 遠回りすることはできます。
2024年早稲田中算数大問①(1)~(3)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#文章題#単位・比と割合・比例・反比例#場合の数#場合の数#早稲田中学
指導講師:
重吉
問題文全文(内容文):
次の問いに答えなさい。
(1) 次の計算をし、約分できない分数で答えなさい。
5/ (2 * 3) + 11/ (3 * 4) + 19/ (4 * 5) + 29/ (5 * 6)
(2)
太郎君はある本を読み始めて最初の5日間は同じページ数を読み進めて、その本を読み始めてあとの3日間は旅行中のため1日あたり6ページ減らして読みました。旅行から帰ったあとは毎日、旅行中の1日あたりの4倍のページ数を読んだところ、 旅行から帰って4日目にはじめて200ページを超え、この日にちょうどこの本を読み終えました。この本は全部で何ページありますか。
(3) 下の図(※動画内参照)のような東西に4本、南北に6本の道があります。南スタート地点から東ゴール、西ゴール、北ゴール地点のいずれかに進む方法は全部で何通りありますか。ただし、南方向には進むことができませんが、北方向,東方向,西方向のいずれかに進むことができます。また、一度通った道を通ることはできませんが、 遠回りすることはできます。
この動画を見る
次の問いに答えなさい。
(1) 次の計算をし、約分できない分数で答えなさい。
5/ (2 * 3) + 11/ (3 * 4) + 19/ (4 * 5) + 29/ (5 * 6)
(2)
太郎君はある本を読み始めて最初の5日間は同じページ数を読み進めて、その本を読み始めてあとの3日間は旅行中のため1日あたり6ページ減らして読みました。旅行から帰ったあとは毎日、旅行中の1日あたりの4倍のページ数を読んだところ、 旅行から帰って4日目にはじめて200ページを超え、この日にちょうどこの本を読み終えました。この本は全部で何ページありますか。
(3) 下の図(※動画内参照)のような東西に4本、南北に6本の道があります。南スタート地点から東ゴール、西ゴール、北ゴール地点のいずれかに進む方法は全部で何通りありますか。ただし、南方向には進むことができませんが、北方向,東方向,西方向のいずれかに進むことができます。また、一度通った道を通ることはできませんが、 遠回りすることはできます。
これどう解く?

2024年吉祥女子中算数大問①(5)~(7)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#平面図形#角度と面積#相似と相似を利用した問題#吉祥女子中学
指導講師:
重吉
問題文全文(内容文):
※図は動画内参照
(5)
下の図の四本の直線AE,BF,CG,DHはすべて平行です。AB:BC:CD = 3:2:4, BF:CG = 5:6 のとき、AE:DH = を最も簡単な整数の比で答えなさい。
(6)
整数Aがあり、283をAで割った余りは、356をAで割った余りよりも4だけ小さく、463をAで割った余りよりも4だけ大きいです。整数Aを答えなさい。
(7)
下の図の三角形ABCと三角形ADEは正三角形です。正三角形ABCの一辺の長さは12 cmで、BDの長さは4 cmです。三角形ADFの面積は正三角形の面積の何倍ですか。
この動画を見る
※図は動画内参照
(5)
下の図の四本の直線AE,BF,CG,DHはすべて平行です。AB:BC:CD = 3:2:4, BF:CG = 5:6 のとき、AE:DH = を最も簡単な整数の比で答えなさい。
(6)
整数Aがあり、283をAで割った余りは、356をAで割った余りよりも4だけ小さく、463をAで割った余りよりも4だけ大きいです。整数Aを答えなさい。
(7)
下の図の三角形ABCと三角形ADEは正三角形です。正三角形ABCの一辺の長さは12 cmで、BDの長さは4 cmです。三角形ADFの面積は正三角形の面積の何倍ですか。
2024年吉祥女子中算数大問①(5)~(7)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#平面図形#角度と面積#相似と相似を利用した問題#吉祥女子中学
指導講師:
重吉
問題文全文(内容文):
(5)
下の図の4本の直線AE,BF,CG,DHはすべて平行です。
AB:BC:CD=3:2:4, BF:CG=5:6のとき、AE:DHwp最も簡単な整数の比で答えなさい。
※図は動画内参照図
(6)
整数Aがあり、283をAで割った余りは、356をAで割った余りよりも4だけ小さく、463をAで割った余りより4だけ大きいです。整数Aを答えなさい。
(7)
下の図の三角形ABCと三角形ADEは正三角形です。正三角形ABCの一辺の長さは12 cmで、BDの長さは4 cmです。三角形ADFの面積は正三角形ABCの面積の何倍ですか。
※図は動画内参照図
この動画を見る
(5)
下の図の4本の直線AE,BF,CG,DHはすべて平行です。
AB:BC:CD=3:2:4, BF:CG=5:6のとき、AE:DHwp最も簡単な整数の比で答えなさい。
※図は動画内参照図
(6)
整数Aがあり、283をAで割った余りは、356をAで割った余りよりも4だけ小さく、463をAで割った余りより4だけ大きいです。整数Aを答えなさい。
(7)
下の図の三角形ABCと三角形ADEは正三角形です。正三角形ABCの一辺の長さは12 cmで、BDの長さは4 cmです。三角形ADFの面積は正三角形ABCの面積の何倍ですか。
※図は動画内参照図
【算数練習】114(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#平面図形その他
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
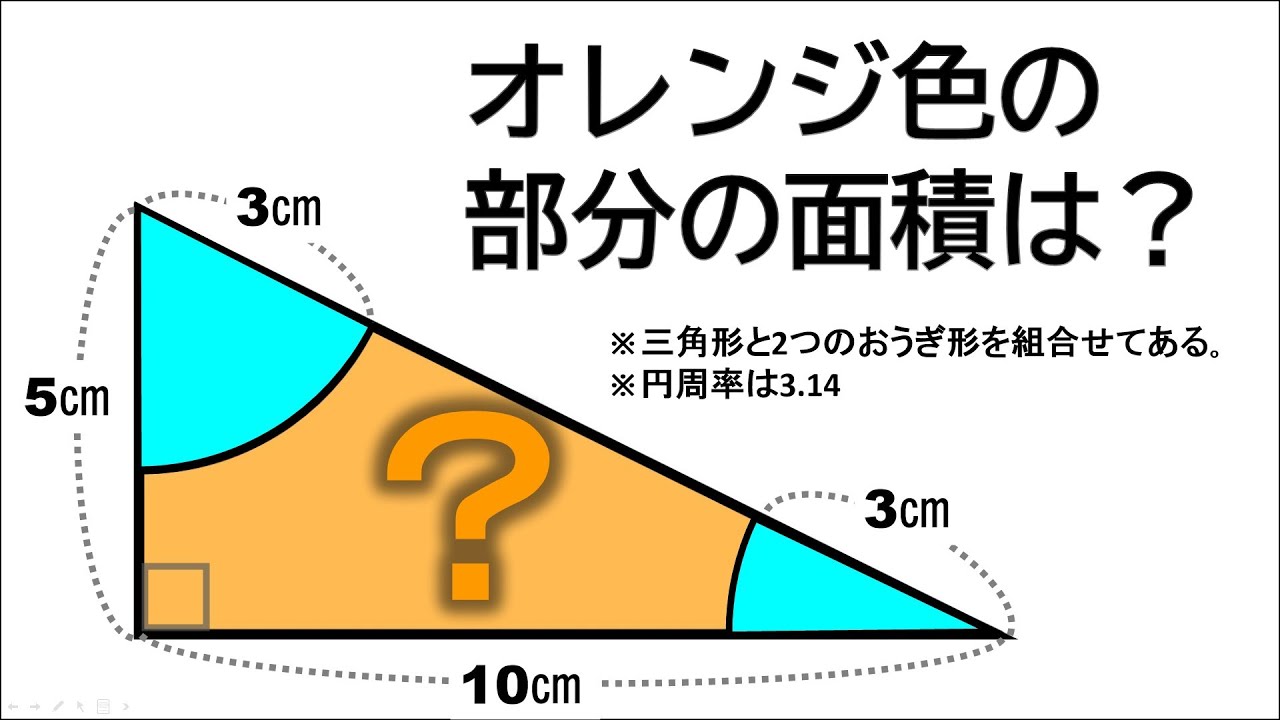
三角形と2つのおうぎ形を組合せてある。
円周率は3.14
*図は動画内参照
オレンジ色の部分の面積は?
この動画を見る
三角形と2つのおうぎ形を組合せてある。
円周率は3.14
*図は動画内参照
オレンジ色の部分の面積は?
2024年吉祥女子中算数大問①(1)~(4)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#文章題#売買損益と食塩水#平均算・過不足算・差集め算・消去算#吉祥女子中学
指導講師:
重吉
問題文全文(内容文):
(1)
次の空欄▭に当てはまる数を求めなさい。
$(\dfrac{1}{3}+2.625\times\Box)\div13-\dfrac{7}{12}=\dfrac{1}{4}$
(2)
次の空欄▭に当てはまる数を求めなさい。
$(0.75-\Box)\times0.5-\dfrac{1}{8}\times(\dfrac{1}{2}-\dfrac{1}{6})=\dfrac{5}{8}$
(3)
10%の食塩水300gに、4%の食塩水を加えて6%の食塩水を作りました。4%の食塩水を何g加えましたか。
(4)
Aさん、Bさん、Cさん、Dさんの四人が算数のテストを受けました。AさんとBさんの平均点は78点でした。また、AさんとCさんとDさんの平均点は75点で、BさんとCさんとDさんの平均点は71点でした。Aさんは何点でしたか。
この動画を見る
(1)
次の空欄▭に当てはまる数を求めなさい。
$(\dfrac{1}{3}+2.625\times\Box)\div13-\dfrac{7}{12}=\dfrac{1}{4}$
(2)
次の空欄▭に当てはまる数を求めなさい。
$(0.75-\Box)\times0.5-\dfrac{1}{8}\times(\dfrac{1}{2}-\dfrac{1}{6})=\dfrac{5}{8}$
(3)
10%の食塩水300gに、4%の食塩水を加えて6%の食塩水を作りました。4%の食塩水を何g加えましたか。
(4)
Aさん、Bさん、Cさん、Dさんの四人が算数のテストを受けました。AさんとBさんの平均点は78点でした。また、AさんとCさんとDさんの平均点は75点で、BさんとCさんとDさんの平均点は71点でした。Aさんは何点でしたか。
2024年吉祥女子中算数大問①(1)~(4)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#文章題#売買損益と食塩水
指導講師:
重吉
問題文全文(内容文):
(1)
次の空欄に当てはまる数を答えなさい。
($\dfrac{1}{3}$ + 2.625 +$ \square$)$ \div $13 - $\dfrac{7}{12}$ = $\dfrac{1}{4}$
(2)
次の空欄に当てはまる数を答えなさい。
(0.75 - $\square$) $\div$ 0.5 - $\dfrac{1}{8}$$ \times $($\dfrac{1}{2}$ - $\dfrac{1}{6}$) = $\dfrac{5}{8}$
(3)
10 %の食塩水300 gに、4 %の食塩水を加えて6 %の食塩水を作りました。4 %の食塩水を何g加えましたか。
(4)
A,B,C.Dの四人が算数のテストを受けました。A,Bの平均点は78点、A,B,Cの平均点は75点、B,C,Dの平均点は71点でした。Aさんは何点でしたか
この動画を見る
(1)
次の空欄に当てはまる数を答えなさい。
($\dfrac{1}{3}$ + 2.625 +$ \square$)$ \div $13 - $\dfrac{7}{12}$ = $\dfrac{1}{4}$
(2)
次の空欄に当てはまる数を答えなさい。
(0.75 - $\square$) $\div$ 0.5 - $\dfrac{1}{8}$$ \times $($\dfrac{1}{2}$ - $\dfrac{1}{6}$) = $\dfrac{5}{8}$
(3)
10 %の食塩水300 gに、4 %の食塩水を加えて6 %の食塩水を作りました。4 %の食塩水を何g加えましたか。
(4)
A,B,C.Dの四人が算数のテストを受けました。A,Bの平均点は78点、A,B,Cの平均点は75点、B,C,Dの平均点は71点でした。Aさんは何点でしたか
【小6算数手元解説】最初の5kmは一定の速さで歩き、その後20%増しにして歩いたら15分早くB地点に着いた【問題文は概要欄】

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある人がA地点からB地点まで歩くのに、A地点から5kmの間はある一定の速さで歩きました。その後、歩く速さを最初の速さよりも20%増して歩いたため、予定より15分早くB地点につきました。もしはじめから増した速さで歩くと、予定より40分早くB地点につくそうです。最初の速さは時速何kmですか。
この動画を見る
ある人がA地点からB地点まで歩くのに、A地点から5kmの間はある一定の速さで歩きました。その後、歩く速さを最初の速さよりも20%増して歩いたため、予定より15分早くB地点につきました。もしはじめから増した速さで歩くと、予定より40分早くB地点につくそうです。最初の速さは時速何kmですか。
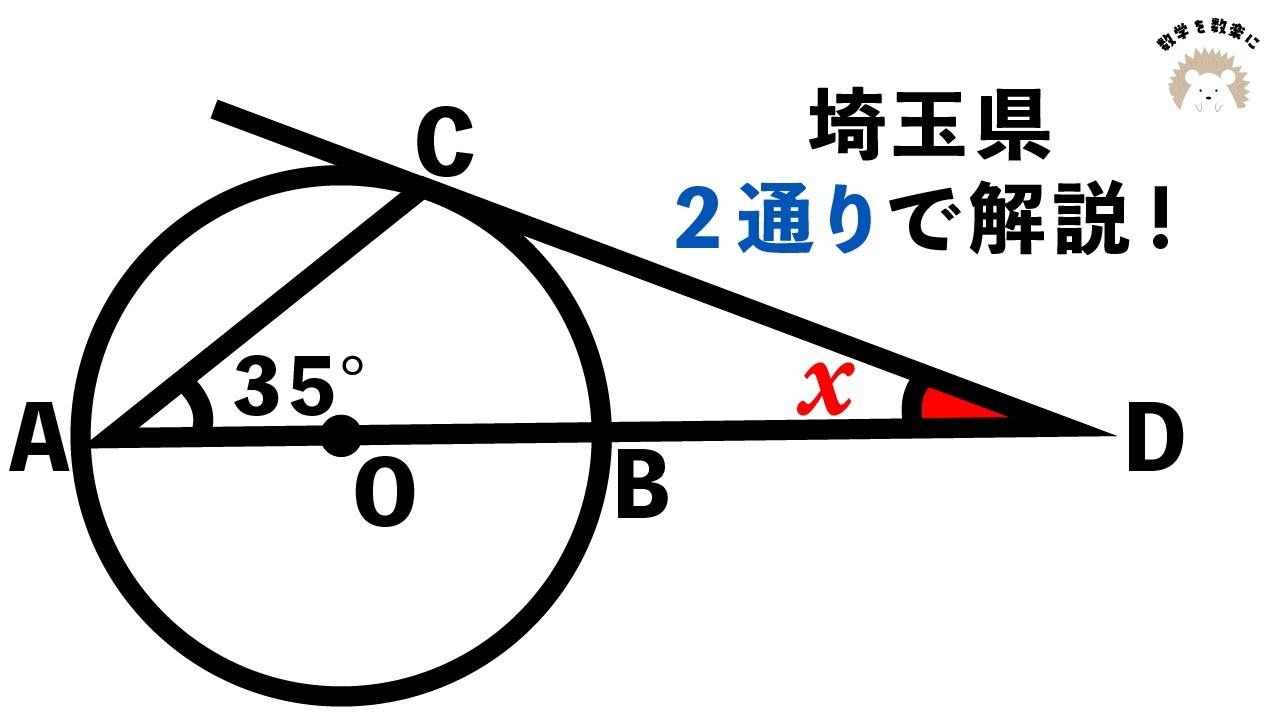
円と接線 2通りで解説 埼玉県
2024年海城中算数大問①(1)~(5)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#海城中学
指導講師:
重吉
問題文全文(内容文):
次の問いに答えなさい。
(1)9÷[4{1/6} +{2.25-1(1/2)}/0.75-2{1/2}]/1.125
(2) 8%の食塩水80g, 6%の食塩水120g,4%の食塩水150g,水▭gを混ぜて5%の食塩水をつくりました。▭にあてはまる数を求めなさい。
(3)現在、父の年齢は兄の年齢の3倍と弟の年齢の和より4歳上です。24年後, 父の年齢は兄と弟の年齢の和に等しくなります。父と弟の年齢の差を求めなさい。
(4)100以上300以下の整数のうち、約数の個数が9個である整数をすべて求めなさい。
(5) 下の図において直線ABとCDは平行で、長さの等しい辺には同じ印がついています。図の角アの大きさを求めなさい。*図は動画内参照
この動画を見る
次の問いに答えなさい。
(1)9÷[4{1/6} +{2.25-1(1/2)}/0.75-2{1/2}]/1.125
(2) 8%の食塩水80g, 6%の食塩水120g,4%の食塩水150g,水▭gを混ぜて5%の食塩水をつくりました。▭にあてはまる数を求めなさい。
(3)現在、父の年齢は兄の年齢の3倍と弟の年齢の和より4歳上です。24年後, 父の年齢は兄と弟の年齢の和に等しくなります。父と弟の年齢の差を求めなさい。
(4)100以上300以下の整数のうち、約数の個数が9個である整数をすべて求めなさい。
(5) 下の図において直線ABとCDは平行で、長さの等しい辺には同じ印がついています。図の角アの大きさを求めなさい。*図は動画内参照
2024年海城中算数大問①(1)~(5)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#過去問解説(学校別)#文章題#売買損益と食塩水#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#平面図形#角度と面積#海城中学
指導講師:
重吉
問題文全文(内容文):
次の問いに答えなさい。
(1)
$9\div\{ 4\dfrac{1}{6}+(2.25-1\dfrac{1}{2})\div0.75-2 \dfrac{1}{2}\}\div1.125$を計算しなさい。
(2)
8 %の食塩水80 g、6 %の食塩水120 g、4 %の食塩水150 g、水$\Box$ gを混ぜて5 %の食塩水を作りました。$\Box$に当てはまる数を求めなさい。
(3)
現在、父の年齢は兄の年齢の三倍と弟の年齢の和より4歳年上です。24年後、父の年齢は兄と弟の年齢の和に等しくなります。父と弟の年齢の差を求めなさい。
(4)
100以上300以下の整数のうち、約数の個数が9個である整数をすべて求めなさい。
(5)※図は動画内参照
下の図において直線ABとCDは平行で、長さの等しい辺には同じ印がついています。図の角アの大きさを求めなさい。
この動画を見る
次の問いに答えなさい。
(1)
$9\div\{ 4\dfrac{1}{6}+(2.25-1\dfrac{1}{2})\div0.75-2 \dfrac{1}{2}\}\div1.125$を計算しなさい。
(2)
8 %の食塩水80 g、6 %の食塩水120 g、4 %の食塩水150 g、水$\Box$ gを混ぜて5 %の食塩水を作りました。$\Box$に当てはまる数を求めなさい。
(3)
現在、父の年齢は兄の年齢の三倍と弟の年齢の和より4歳年上です。24年後、父の年齢は兄と弟の年齢の和に等しくなります。父と弟の年齢の差を求めなさい。
(4)
100以上300以下の整数のうち、約数の個数が9個である整数をすべて求めなさい。
(5)※図は動画内参照
下の図において直線ABとCDは平行で、長さの等しい辺には同じ印がついています。図の角アの大きさを求めなさい。
【算数練習】113(”大人”は頭の体操)