 大学入試解答速報
大学入試解答速報
 大学入試解答速報
大学入試解答速報
2024年共通テスト徹底解説〜数学ⅡB第5問ベクトル〜福田の入試問題解説

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト#数C
指導講師:
福田次郎
問題文全文(内容文):
共通テスト2024の数学ⅡB第5問ベクトルを徹底解説します
この動画を見る
共通テスト2024の数学ⅡB第5問ベクトルを徹底解説します
二次試験の英語、こう対策すれば伸びます【前期試験・私立入試】

単元:
#英語(高校生)#英作文#自由英作文#英単語#英語
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【前期試験・私立入試】二次試験の英語 対策法説明動画です
この動画を見る
【前期試験・私立入試】二次試験の英語 対策法説明動画です
2024年共通テスト徹底解説〜数学ⅠA第2問(1)2次関数〜福田の入試問題解説

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
共通テスト2024の数学ⅠA第2問(2)2次関数を徹底解説します
2024共通テスト過去問
この動画を見る
共通テスト2024の数学ⅠA第2問(2)2次関数を徹底解説します
2024共通テスト過去問
2024年共通テスト徹底解説〜数学ⅡB第4問数列〜福田の入試問題解説

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト#数B
指導講師:
福田次郎
問題文全文(内容文):
共通テスト2024の数学ⅡB第4問数列を徹底解説します
2024共通テスト過去問
この動画を見る
共通テスト2024の数学ⅡB第4問数列を徹底解説します
2024共通テスト過去問
2024年共通テスト徹底解説〜数学ⅡB第2問微分積分〜福田の入試問題解説

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
共通テスト2024の数学ⅡB第2問微分積分を徹底解説します
2024共通テスト過去問
この動画を見る
共通テスト2024の数学ⅡB第2問微分積分を徹底解説します
2024共通テスト過去問
2024年共通テスト徹底解説〜数学ⅡB第1問(2)整式の除法〜福田の入試問題解説

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
共通テスト2024の数学ⅡB第1問(2)整数の除法を徹底解説します
2024共通テスト過去問
この動画を見る
共通テスト2024の数学ⅡB第1問(2)整数の除法を徹底解説します
2024共通テスト過去問
2024年共通テスト徹底解説〜数学ⅡB第1問(1)対数関数〜福田の入試問題解説

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
共通テスト2024の数学ⅡB第1問(1)対数関数を徹底解説します
2024共通テスト過去問
この動画を見る
共通テスト2024の数学ⅡB第1問(1)対数関数を徹底解説します
2024共通テスト過去問
2024年共通テスト徹底解説〜数学ⅠA第2問(2)データの分析〜福田の入試問題解説

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
共通テスト2024の数学ⅠA第2問(2)データの分析を徹底解説します
2024共通テスト過去問
この動画を見る
共通テスト2024の数学ⅠA第2問(2)データの分析を徹底解説します
2024共通テスト過去問
【現役講師による詳しい解説と講評!】2024年共通テスト化学解答解説〔現役塾講師解説、高校化学、化学基礎〕

2024年共通テスト徹底解説〜数学ⅠA第5問図形の性質〜福田の入試問題解説

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#方べきの定理と2つの円の関係#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
第5 問(1) $\triangle AQD$と直線CEに着目すると$\dfrac{QR}{RD}・\dfrac{DS}{SA}・\dfrac{ア}{CQ}=1$が成り立つのでQR:RD=イ:ウ となる。また、$\triangle AQD$と直線BEに着目するとQB:BD=エ:オ となる。
したがって、BQ:QR:RD=エ:イ:ウとなる個tが分かる。
(2)5点P,Q,R,S,Tが同一演習場にあるとし、AC=8とする。
(i)5点A,P,Q,S,Tに着目すると、AT:ST=1:2より、AT=$\sqrt{ カ }$となる。さらに5点D,Q,R,S,Tに着目すると$DR=4\sqrt{ 3 }$となることがわかる。
( 2 ) 3 点 A , B, C を通る円と点 D の位置関係を次の構想に基づいて調べよう。
構想:線分 AC と BD の交点 Q に着目し、 AQ $\cdot$ CQ と BQ $\cdot$ DQ の大小を比べる。
まず AQ $\cdot$ CQ = 5 $\cdot$ 3 = 15 かっ BQ $\cdot$ DQ =キクであるから
AQ$\cdot$CQ ケ BQ$\cdot$DQ $\cdots$①
が成り立つ。また、3点A,B,Cを通る\と直線BDとの交点のうち、Bと異なる点をXとするとAQ$\cdot$CQ ケ BQ$\cdot$XQ $\cdots$②
①②の左辺は同じなので①②の右辺と比べることによりXQ サ DQが得られる。したがって点DはA,B,Cを通る円の シ にある。
(2)3 点 C , D , E を通る円と 2 点 A , B の位置関係について調べよう。この星形の図形において、さらにCR = RS = SE = 3 となることがわかる。したがって、点 A は 3 点 C, E, D を通る円の ス にあり、点 B は 3 点 C, E, D を通る円の セ にある。
2024共通テスト過去問
この動画を見る
第5 問(1) $\triangle AQD$と直線CEに着目すると$\dfrac{QR}{RD}・\dfrac{DS}{SA}・\dfrac{ア}{CQ}=1$が成り立つのでQR:RD=イ:ウ となる。また、$\triangle AQD$と直線BEに着目するとQB:BD=エ:オ となる。
したがって、BQ:QR:RD=エ:イ:ウとなる個tが分かる。
(2)5点P,Q,R,S,Tが同一演習場にあるとし、AC=8とする。
(i)5点A,P,Q,S,Tに着目すると、AT:ST=1:2より、AT=$\sqrt{ カ }$となる。さらに5点D,Q,R,S,Tに着目すると$DR=4\sqrt{ 3 }$となることがわかる。
( 2 ) 3 点 A , B, C を通る円と点 D の位置関係を次の構想に基づいて調べよう。
構想:線分 AC と BD の交点 Q に着目し、 AQ $\cdot$ CQ と BQ $\cdot$ DQ の大小を比べる。
まず AQ $\cdot$ CQ = 5 $\cdot$ 3 = 15 かっ BQ $\cdot$ DQ =キクであるから
AQ$\cdot$CQ ケ BQ$\cdot$DQ $\cdots$①
が成り立つ。また、3点A,B,Cを通る\と直線BDとの交点のうち、Bと異なる点をXとするとAQ$\cdot$CQ ケ BQ$\cdot$XQ $\cdots$②
①②の左辺は同じなので①②の右辺と比べることによりXQ サ DQが得られる。したがって点DはA,B,Cを通る円の シ にある。
(2)3 点 C , D , E を通る円と 2 点 A , B の位置関係について調べよう。この星形の図形において、さらにCR = RS = SE = 3 となることがわかる。したがって、点 A は 3 点 C, E, D を通る円の ス にあり、点 B は 3 点 C, E, D を通る円の セ にある。
2024共通テスト過去問
共通テスト_ボーダーどうなるの?【概要欄必読】

単元:
#大学入試解答速報#数学#共通テスト#英語#化学#物理#共通テスト#共通テスト#共通テスト#世界史#共通テスト
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
共通テスト_ボーダーがどのぐらいになるか。解説動画です
この動画を見る
共通テスト_ボーダーがどのぐらいになるか。解説動画です
2024年共通テスト解答解説速報 化学 【問題別にチャプターになっていますので概要欄より見たい問題に飛んでください】

単元:
#化学#大学入試過去問(化学)#共通テスト#理科(高校生)#大学入試解答速報#化学#共通テスト
指導講師:
理数個別チャンネル
問題文全文(内容文):
こちらの動画は、2024年1月14日(日)に実施された、共通テスト化学解答速報です。
あくまで当チャンネルの講師が独自に解説をしているものですので、万が一内容に間違いがございましたらご容赦ください。
この動画を見る
こちらの動画は、2024年1月14日(日)に実施された、共通テスト化学解答速報です。
あくまで当チャンネルの講師が独自に解説をしているものですので、万が一内容に間違いがございましたらご容赦ください。
2024年共通テスト解答速報〜数学ⅠA第4問整数の性質〜福田の入試問題解説

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
T 3 、 T 4 、 T 6 を次のようなタイマ ー とする。
T3 : 3 進数を 3 桁表示するタイマ ー
T4 : 4 進数を 3 桁表示するタイマ ー
T 6 : 6 進数を 3 裄表示するタイマ ー
なお、第進数とは進法で表された数のことである。これらのタイマ ー は.すべて次の表示方法に従うものとする。
表示方法
(a) スタ ー トした時点でタイマ ー は 000 と表示されている。
(b)タイマ ー は、スタ ー トした後、表示される数が1秒ごとに1ずつ増えていき、3 析で表示できる最大の数が表示された1秒後に.表示が000に戻る。
(c)タイマ ー は表示が 000 に戻った後も(b )と同様に表示される数が 1秒ごとに1ずつ増えていき、3 裄で表示できる最大の数が表示された1秒後に、表示が 000 に戻るという動作を繰り返す。
例えば、 T3 はスタ ー トしてから 3 進数でに$12_{ (3) }$秒後に012 と表示される。その後 222 と表示された1秒後に表示が000に戻り、その$12_{ (3) }$秒後に再び012と表示される。
( 1 ) T6 は、スタ ー トしてから 10 進数で 40 秒後にアイウと表示される。T4 は、スタ ー トしてから 2 進数で$10011_{ (2) }$秒後にエオカと表示される。
( 2 ) T 4 をスタ ー トさせた後、初めて表示が 000 に戻るのは、スタ ー トしてから10 進数でキク秒後であり、その後もキク秒ごとに表示が 000 に戻る。同様の考察を T 6 に対しても行うことにより、 T 4 と T 6 を同時にスタートさせた後、初めて両方の表示が同時に 000 に戻るのは.スタ ー トしてから 10 進でケコサシ秒後であることがわかる。
( 3 ) 0 以上の整数$\ell$に対して、T 4 をスタ ー トさせた$\ell$秒後に T4 が 012と表示されることと
$\ell$をスセで割った余りがソであることは同値である。ただしスセとソは10進法で表されているものとする。T3 についても同様の考察を行うことにより、次のことがわかる。T3 と T4 を同時にスタ ー トさせてから、初めて両方が同時に 012 と表示されるまでの時間をm秒とするとき、mは 10 進法でタチツと表される。
また、 T4とT6 の表示に関する記述として.次の0~3のうち、正しいものはテである。
0 T4 と T6 を同時にスタ ー トさせてから、m秒後より前に初めて両方が同時に 012 と表示される。
1 T4 と T6 を同時にスタ ー トさせてから、ちょうどm秒後に初めて両方が同時に 0 と表示される。
2 T4 と T6 を同時にスタ ー トさせてから、m秒後より後に初めて両方が同時に 012 と表示される。
3 T4 と T6 を同時にスタ一トさせてから、両方が同時に 012 と表示されることはない。
2024共通テスト過去問
この動画を見る
T 3 、 T 4 、 T 6 を次のようなタイマ ー とする。
T3 : 3 進数を 3 桁表示するタイマ ー
T4 : 4 進数を 3 桁表示するタイマ ー
T 6 : 6 進数を 3 裄表示するタイマ ー
なお、第進数とは進法で表された数のことである。これらのタイマ ー は.すべて次の表示方法に従うものとする。
表示方法
(a) スタ ー トした時点でタイマ ー は 000 と表示されている。
(b)タイマ ー は、スタ ー トした後、表示される数が1秒ごとに1ずつ増えていき、3 析で表示できる最大の数が表示された1秒後に.表示が000に戻る。
(c)タイマ ー は表示が 000 に戻った後も(b )と同様に表示される数が 1秒ごとに1ずつ増えていき、3 裄で表示できる最大の数が表示された1秒後に、表示が 000 に戻るという動作を繰り返す。
例えば、 T3 はスタ ー トしてから 3 進数でに$12_{ (3) }$秒後に012 と表示される。その後 222 と表示された1秒後に表示が000に戻り、その$12_{ (3) }$秒後に再び012と表示される。
( 1 ) T6 は、スタ ー トしてから 10 進数で 40 秒後にアイウと表示される。T4 は、スタ ー トしてから 2 進数で$10011_{ (2) }$秒後にエオカと表示される。
( 2 ) T 4 をスタ ー トさせた後、初めて表示が 000 に戻るのは、スタ ー トしてから10 進数でキク秒後であり、その後もキク秒ごとに表示が 000 に戻る。同様の考察を T 6 に対しても行うことにより、 T 4 と T 6 を同時にスタートさせた後、初めて両方の表示が同時に 000 に戻るのは.スタ ー トしてから 10 進でケコサシ秒後であることがわかる。
( 3 ) 0 以上の整数$\ell$に対して、T 4 をスタ ー トさせた$\ell$秒後に T4 が 012と表示されることと
$\ell$をスセで割った余りがソであることは同値である。ただしスセとソは10進法で表されているものとする。T3 についても同様の考察を行うことにより、次のことがわかる。T3 と T4 を同時にスタ ー トさせてから、初めて両方が同時に 012 と表示されるまでの時間をm秒とするとき、mは 10 進法でタチツと表される。
また、 T4とT6 の表示に関する記述として.次の0~3のうち、正しいものはテである。
0 T4 と T6 を同時にスタ ー トさせてから、m秒後より前に初めて両方が同時に 012 と表示される。
1 T4 と T6 を同時にスタ ー トさせてから、ちょうどm秒後に初めて両方が同時に 0 と表示される。
2 T4 と T6 を同時にスタ ー トさせてから、m秒後より後に初めて両方が同時に 012 と表示される。
3 T4 と T6 を同時にスタ一トさせてから、両方が同時に 012 と表示されることはない。
2024共通テスト過去問
2024年共通テスト化学の講評と全問解説

【現役講師による詳しい解説と講評!】2024年共通テスト化学基礎解答解説〔現役塾講師解説、高校化学、化学基礎〕

単元:
#化学#大学入試過去問(化学)#共通テスト#理科(高校生)#大学入試解答速報#化学#共通テスト
指導講師:
3rd School
問題文全文(内容文):
2024年共通テスト化学基礎解説動画です
この動画を見る
2024年共通テスト化学基礎解説動画です
2024年共通テスト解答速報〜数学ⅠA第1問(2)〜福田の入試問題解説

単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角形の辺の比(内分・外分・二等分線)#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
図 1 のように、電柱の影の先端は坂の斜面(以下、坂)にあるとする。また、坂には傾斜を表す道路標識が設置されていてをそこには 7 %と表示されているとする。電柱の太さと影の幅は無視して考えるものとする。また。地面と坂は平面であるとし、地面と坂が交わってできる直線を$\ell$とする。電柱の先端を点 A とし、根もとを点 B とする。電柱の影について。地面にある部分を線分 BC とし、坂にある部分を線分 CD とする。線分BC、CDがそれぞれ$\ell$と重直であるとき、電柱の影は坂に向かってまっすぐにのびているということにする。
※図は動画内参照
電柱の影が坂に向かってまっすぐにのびているとする。このとき、 4 点 A.B. C. D を通る平面は$\ell$と重直である。その平面において、図 2 のように、直線 ADと直線BCの交点を P とすると、太陽高度とは $\angle APB$の大きさのことである。
※図は動画内参照
道路標識の 7 %という表示は、この坂をのぼったとき、100m の水平距離に対して 7m の割合で高くなることを示している。nを1以上 9 以下の整数とするとき、坂の傾斜角$\angle DCP$の大きさについて
$n° \lt \angle DCP \lt n°+1°$
を満たすnの値は シ である。
以下では、$\angle DCP$の大きさは、ちょうどシ°であるとする。
ある日、電柱の影が坂に向かってまっすぐにのびていたとき、影の長さを調べたところBC= 7 m、 CD= 4 m であり、太陽高度は $angle\ APB$=45°であった。点 D から直線 AB に重直な直線を引き、直物 AB との交点を E とするとき
BE=ス×セm
であり
DE=(ソ+アタ×チ)m
である。よって電柱の高さは、小数点第2位で四捨五入するとソmであることがわかる。
別の日、電柱の影が坂に向かってまっすぐにのびていたときの太陽高度は刻= 42°であった。電住の高さがわかったので、前回調べた日からの影の長さの変化を知ることができる。電柱の影について、坂にある第分の長さは
$\dfrac{AB-テ×ト}{ナ+ニ×ト}m$
である。AB=ツmとして、これを計算することにより、この日の電柱の陰について、坂にある部分の長さは、前回調べた4mより約1.2mだけ長いことが分かる。
2024共通テスト過去問
この動画を見る
図 1 のように、電柱の影の先端は坂の斜面(以下、坂)にあるとする。また、坂には傾斜を表す道路標識が設置されていてをそこには 7 %と表示されているとする。電柱の太さと影の幅は無視して考えるものとする。また。地面と坂は平面であるとし、地面と坂が交わってできる直線を$\ell$とする。電柱の先端を点 A とし、根もとを点 B とする。電柱の影について。地面にある部分を線分 BC とし、坂にある部分を線分 CD とする。線分BC、CDがそれぞれ$\ell$と重直であるとき、電柱の影は坂に向かってまっすぐにのびているということにする。
※図は動画内参照
電柱の影が坂に向かってまっすぐにのびているとする。このとき、 4 点 A.B. C. D を通る平面は$\ell$と重直である。その平面において、図 2 のように、直線 ADと直線BCの交点を P とすると、太陽高度とは $\angle APB$の大きさのことである。
※図は動画内参照
道路標識の 7 %という表示は、この坂をのぼったとき、100m の水平距離に対して 7m の割合で高くなることを示している。nを1以上 9 以下の整数とするとき、坂の傾斜角$\angle DCP$の大きさについて
$n° \lt \angle DCP \lt n°+1°$
を満たすnの値は シ である。
以下では、$\angle DCP$の大きさは、ちょうどシ°であるとする。
ある日、電柱の影が坂に向かってまっすぐにのびていたとき、影の長さを調べたところBC= 7 m、 CD= 4 m であり、太陽高度は $angle\ APB$=45°であった。点 D から直線 AB に重直な直線を引き、直物 AB との交点を E とするとき
BE=ス×セm
であり
DE=(ソ+アタ×チ)m
である。よって電柱の高さは、小数点第2位で四捨五入するとソmであることがわかる。
別の日、電柱の影が坂に向かってまっすぐにのびていたときの太陽高度は刻= 42°であった。電住の高さがわかったので、前回調べた日からの影の長さの変化を知ることができる。電柱の影について、坂にある第分の長さは
$\dfrac{AB-テ×ト}{ナ+ニ×ト}m$
である。AB=ツmとして、これを計算することにより、この日の電柱の陰について、坂にある部分の長さは、前回調べた4mより約1.2mだけ長いことが分かる。
2024共通テスト過去問
【2024年共通テスト解答速報(2日目)】日本最速解答速報LIVE|数学ⅠA→ⅡB→物理 ※冒頭7分55秒まで音声が乱れております。申し訳ございません。

単元:
#大学入試過去問(数学)#物理#センター試験・共通テスト関連#共通テスト#大学入試過去問(物理)#数学(高校生)#理科(高校生)#大学入試解答速報#数学#共通テスト#物理#共通テスト#共通テスト
指導講師:
理数個別チャンネル
問題文全文(内容文):
10000人登録目指しています。
何卒チャンネル登録お願いします!!!
※冒頭7分55秒まで音声が乱れております。申し訳ございません。
◆解答のまとめ◆
https://note.com/kobetsu_teacher/n/nf15e55b4c121
◆出演者◆
・TAKAHASHI名人
https://www.youtube.com/playlist?list=PLdLgDY469Qr7UEbDX8OecmSefwQulR35t
・ゆう☆たろう
https://www.youtube.com/playlist?list=PLdLgDY469Qr5zKa9ZgI9StW_-cNtbBDsn
・烈's study
https://www.youtube.com/playlist?list=PLdLgDY469Qr7QbP6MrNjpltLkbkyaggpv
・理数大明神
https://www.youtube.com/playlist?list=PLdLgDY469Qr6TpcFul6_A9hu5xZ1bQjNU
◆スタッフ◆
しまだじろう
https://www.youtube.com/playlist?list=PLdLgDY469Qr5kqaeicgkr6YhPZdkMEB3k
◆ドーナツ差し入れありがとう!!◆
岡ちゃん先生
https://www.youtube.com/playlist?list=PLdLgDY469Qr4OulJQO0KGCDMdykOS6pnX
◎対数の領域の問題で間違えた方はこちらを是非見てください!
(インタビューで烈's study!先生が言っていた動画です)
https://youtu.be/ZAXcZQC_sjw
◎ベクトルで間違えた方はこちらを是非見てください!
(インタビューでゆう☆たろう先生が言っていた動画です)
https://youtu.be/CYcQZEYqXj8
produced by 質問解決DB
https://kaiketsu-db.net/
produced by 理数個別チャンネル
https://www.youtube.com/@UCdQ0y9lyNRKcbH8dv2janrw
この動画を見る
10000人登録目指しています。
何卒チャンネル登録お願いします!!!
※冒頭7分55秒まで音声が乱れております。申し訳ございません。
◆解答のまとめ◆
https://note.com/kobetsu_teacher/n/nf15e55b4c121
◆出演者◆
・TAKAHASHI名人
https://www.youtube.com/playlist?list=PLdLgDY469Qr7UEbDX8OecmSefwQulR35t
・ゆう☆たろう
https://www.youtube.com/playlist?list=PLdLgDY469Qr5zKa9ZgI9StW_-cNtbBDsn
・烈's study
https://www.youtube.com/playlist?list=PLdLgDY469Qr7QbP6MrNjpltLkbkyaggpv
・理数大明神
https://www.youtube.com/playlist?list=PLdLgDY469Qr6TpcFul6_A9hu5xZ1bQjNU
◆スタッフ◆
しまだじろう
https://www.youtube.com/playlist?list=PLdLgDY469Qr5kqaeicgkr6YhPZdkMEB3k
◆ドーナツ差し入れありがとう!!◆
岡ちゃん先生
https://www.youtube.com/playlist?list=PLdLgDY469Qr4OulJQO0KGCDMdykOS6pnX
◎対数の領域の問題で間違えた方はこちらを是非見てください!
(インタビューで烈's study!先生が言っていた動画です)
https://youtu.be/ZAXcZQC_sjw
◎ベクトルで間違えた方はこちらを是非見てください!
(インタビューでゆう☆たろう先生が言っていた動画です)
https://youtu.be/CYcQZEYqXj8
produced by 質問解決DB
https://kaiketsu-db.net/
produced by 理数個別チャンネル
https://www.youtube.com/@UCdQ0y9lyNRKcbH8dv2janrw
2024年共通テスト速報〜数学ⅠA第1問の(1)〜福田の入試解説

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
$n \lt 2\sqrt{ 13 } \lt n+1$を満たす整数nはアである。
実数a,bを$a=2\sqrt{ 13 }$-ア,b=$\frac{1}{a}$で定める。このとき
$b=\frac{イ+2\sqrt{13}}{ウ}$である。また、$a^2-9b^2=エオカ\sqrt{13}$である。
①(7$\lt 2\sqrt{13} \lt 8$)から$\frac{7}{2} \lt \sqrt{13} \lt 4$が成り立つ。
①と④($b=\frac{7+2\sqrt{13}}{3}$)から$\frac{m}{ウ} \lt b \lt \frac{m+1}{ウ}$を満たすmはキク
よって③($b=\frac{1}{a}$)から$\frac{a}{15} \lt a \lt \frac{ウ}{14}$・・・⑥が成り立つ。
$\sqrt{13}$の整数部分はケであり、②($a=2\sqrt{13}-7$)と⑥から$\sqrt{13}$の小数点第1位の数字はコ、小数点第2位の数字はサである。
2024共通テスト過去問
この動画を見る
$n \lt 2\sqrt{ 13 } \lt n+1$を満たす整数nはアである。
実数a,bを$a=2\sqrt{ 13 }$-ア,b=$\frac{1}{a}$で定める。このとき
$b=\frac{イ+2\sqrt{13}}{ウ}$である。また、$a^2-9b^2=エオカ\sqrt{13}$である。
①(7$\lt 2\sqrt{13} \lt 8$)から$\frac{7}{2} \lt \sqrt{13} \lt 4$が成り立つ。
①と④($b=\frac{7+2\sqrt{13}}{3}$)から$\frac{m}{ウ} \lt b \lt \frac{m+1}{ウ}$を満たすmはキク
よって③($b=\frac{1}{a}$)から$\frac{a}{15} \lt a \lt \frac{ウ}{14}$・・・⑥が成り立つ。
$\sqrt{13}$の整数部分はケであり、②($a=2\sqrt{13}-7$)と⑥から$\sqrt{13}$の小数点第1位の数字はコ、小数点第2位の数字はサである。
2024共通テスト過去問
【解答速報!全問完全解説60分★受験世界史のYES:第4弾】『2024年入試・共通テスト世界史』~私大受験・国公立2次受験に向かう前に知識を再確認!

単元:
#社会(高校生)#世界史#大学入試過去問・共通テスト・模試関連#大学入試解答速報#世界史#共通テスト
指導講師:
世界史予備校講師佐藤幸夫 Yukio Sato チャンネル
問題文全文(内容文):
2024年入試の“ラストスパートのはじまり”です。
2023年は、家庭の事情で多忙であったので、なかなか〈受験生のための世界史class(セカジュ)〉の配信が滞っておりました😢。ようやく、落ち着きましたので、12月後半の今日から、入試直前恒例の【YES(yukio`s Examination Service)】を開始いたします。
このYESは、代々木ゼミナールの世界史講師として33年間培った「合格へのノウハウ」を無料で惜しみなく配信する〈セカジュ〉のイベント的動画です。受験と併願の心得・志望校別の対策の技・過去問の使い方・2024年入試の世界史流行を狙う・共通テスト対策・共通テスト速報(解答・解説)・関関同立対策・早慶対策・GARCH対策・直前準備と心得・2月1日~21日の入試速報(明日への狙いなど)・国公立2次対策・論述の心得など…12月後半~2月後半までの無料の入試Serviceです。
この動画を見る
2024年入試の“ラストスパートのはじまり”です。
2023年は、家庭の事情で多忙であったので、なかなか〈受験生のための世界史class(セカジュ)〉の配信が滞っておりました😢。ようやく、落ち着きましたので、12月後半の今日から、入試直前恒例の【YES(yukio`s Examination Service)】を開始いたします。
このYESは、代々木ゼミナールの世界史講師として33年間培った「合格へのノウハウ」を無料で惜しみなく配信する〈セカジュ〉のイベント的動画です。受験と併願の心得・志望校別の対策の技・過去問の使い方・2024年入試の世界史流行を狙う・共通テスト対策・共通テスト速報(解答・解説)・関関同立対策・早慶対策・GARCH対策・直前準備と心得・2月1日~21日の入試速報(明日への狙いなど)・国公立2次対策・論述の心得など…12月後半~2月後半までの無料の入試Serviceです。
2024年共通テスト英語リーディング解答速報LIVE【ネイティブも解けないレベルで難しすぎ】

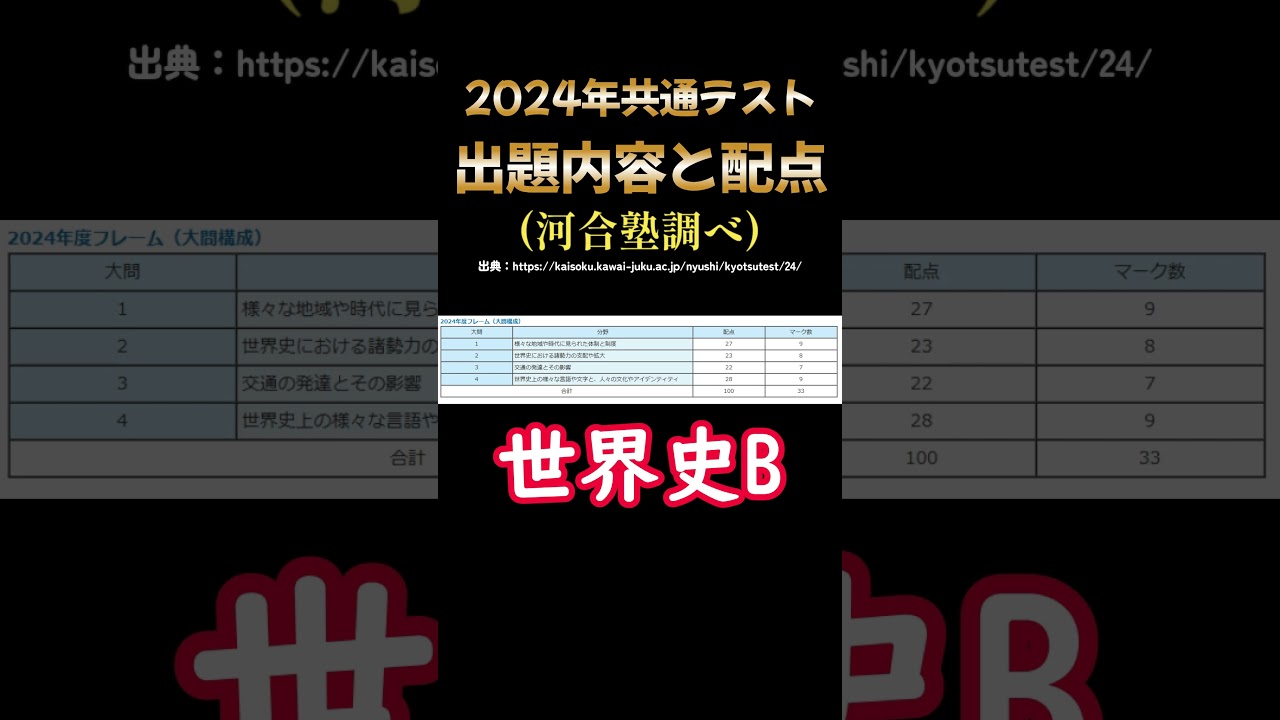
2024年共通テスト社会の出題範囲と配点速報 #shorts #共通テスト #世界史 #日本史 #地理 #倫理政経
単元:
#社会(高校生)#日本史#世界史#大学入試過去問・共通テスト・模試関連#大学入試過去問・共通テスト・模試関連#大学入試解答速報#世界史#共通テスト
指導講師:
理数個別チャンネル
問題文全文(内容文):
2024年共通テスト社会の出題範囲と配点速報
この動画を見る
2024年共通テスト社会の出題範囲と配点速報
【共テ直前!!】共通テスト数学で知っておくと得する公式まとめ!!【数学IA・IIB】

単元:
#数学#共通テスト
指導講師:
3rd School
問題文全文(内容文):
共通テスト数学で知っておくと得する公式についてまとめました。
図形編①トレミーの定理
図形編②四角形の面積
図形編③角の二等分線関連
代数編①二次関数の表現
代数編②面積のあれこれ
この動画を見る
共通テスト数学で知っておくと得する公式についてまとめました。
図形編①トレミーの定理
図形編②四角形の面積
図形編③角の二等分線関連
代数編①二次関数の表現
代数編②面積のあれこれ
【直前に確認したいことチェック!!】 共通テスト化学基礎・化学最終チェック事項&出そうなところのポイント

【直前に15点UP】共テ英語リーディング大門別で解き方を総解説【手元解説】(2023本試 *一部2022本試)

単元:
#英語(高校生)#共通テスト#英語#共通テスト
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
共通テスト英語リーディング大門別で解き方を総解説
この動画を見る
共通テスト英語リーディング大門別で解き方を総解説
共通テスト出題予想2024_ココが出ます【地歴公民・数学・英語・国語】

単元:
#共通テスト#英語(高校生)#国語(高校生)#社会(高校生)#日本史#世界史#共通テスト#共通テスト(古文)#数学(高校生)#大学入試解答速報#数学#共通テスト#英語#共通テスト#世界史#共通テスト
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
共通テスト出題予想2024【地歴公民・数学・英語・国語】
この動画を見る
共通テスト出題予想2024【地歴公民・数学・英語・国語】
サムネの裏技、知らないとか無いよね??【共通テストの裏技】

単元:
#大学入試解答速報#数学#共通テスト#英語#化学#物理#共通テスト#共通テスト#共通テスト#世界史#共通テスト
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
共通テストの裏技紹介動画です
この動画を見る
共通テストの裏技紹介動画です
共通テスト数学を、数学者が解いてみた結果【大学受験数学】

単元:
#数学#共通テスト
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
第5問 (選択問題) (配点 20)
△ABCの重心をGとし、線分AG上で点Aとは異なる位置に点Dをとる。直 線AGと辺BCの交点をEとする。また、直線BC上で辺BC上にはない位置に 点Fをとる。直線DFと辺ABの交点をP、直線DFと辺ACの交点をQとす る。
(1) 点Dは線分AGの中点であるとする。このとき、△ABCの形状に関係なく
AD/DE=ア/イ
である。また、点下の位置に関係なく
BP/AP=ウ×エ/オ
CQ/AQ = カ×キ/ク
であるので、つねに
BP/AP + CQ/AQ = ケ
となる。
エ
オ
キ
ク
の解答群(同じものを繰り返し選ん
でもよい。)
①BC
➁BF
③CF
④EF
⑤FP
⑥FQ
⑦PQ
数学1、数字A
[2] 以下の問題を解答するにあたっては、必要に応じて41 ページの三角比の 表を用いてもよい。
太郎さんと花子さんは、キャンプ場のガイドブックにある地図を見なが ら、後のように話している。
参考図
太郎:キャンプ場の地点Aから山頂Bを見上げる角度はどれくらいか な。
花子:地図アプリを使って、地点Aと山頂Bを含む断面図を調べた ら、図1のようになったよ。点Cは、山頂Bから地点Aを通る 水平面に下ろした垂線とその水平面との交点のことだよ。
太郎:図1の角度は、AC、BCの長さを定規で測って、三角比の表を 用いて調べたら16°だったよ。
花子:本当に16なの? 図1の鉛直方向の縮尺と水平方向の縮尺は等 しいのかな?
数学Ⅰ・数学A
[3] 外接円の半径が3である△ABCを考える。点Aから直線BCに引いた垂 線と直線BCとの交点をDとする。
(1) AB = 5 AC=4とする。このとき
この動画を見る
第5問 (選択問題) (配点 20)
△ABCの重心をGとし、線分AG上で点Aとは異なる位置に点Dをとる。直 線AGと辺BCの交点をEとする。また、直線BC上で辺BC上にはない位置に 点Fをとる。直線DFと辺ABの交点をP、直線DFと辺ACの交点をQとす る。
(1) 点Dは線分AGの中点であるとする。このとき、△ABCの形状に関係なく
AD/DE=ア/イ
である。また、点下の位置に関係なく
BP/AP=ウ×エ/オ
CQ/AQ = カ×キ/ク
であるので、つねに
BP/AP + CQ/AQ = ケ
となる。
エ
オ
キ
ク
の解答群(同じものを繰り返し選ん
でもよい。)
①BC
➁BF
③CF
④EF
⑤FP
⑥FQ
⑦PQ
数学1、数字A
[2] 以下の問題を解答するにあたっては、必要に応じて41 ページの三角比の 表を用いてもよい。
太郎さんと花子さんは、キャンプ場のガイドブックにある地図を見なが ら、後のように話している。
参考図
太郎:キャンプ場の地点Aから山頂Bを見上げる角度はどれくらいか な。
花子:地図アプリを使って、地点Aと山頂Bを含む断面図を調べた ら、図1のようになったよ。点Cは、山頂Bから地点Aを通る 水平面に下ろした垂線とその水平面との交点のことだよ。
太郎:図1の角度は、AC、BCの長さを定規で測って、三角比の表を 用いて調べたら16°だったよ。
花子:本当に16なの? 図1の鉛直方向の縮尺と水平方向の縮尺は等 しいのかな?
数学Ⅰ・数学A
[3] 外接円の半径が3である△ABCを考える。点Aから直線BCに引いた垂 線と直線BCとの交点をDとする。
(1) AB = 5 AC=4とする。このとき
共通テスト英語リーディング対策講義【ギリギリでも点数は上がる】

単元:
#英語(高校生)#英語#共通テスト
指導講師:
Morite2 English Channel
問題文全文(内容文):
Skimming サッと全体を読み概要がわかる
Scanning 必要な情報を抜きとる
この動画を見る
Skimming サッと全体を読み概要がわかる
Scanning 必要な情報を抜きとる
【共通テストレベル別】頻出英単語テスト60問_何点とれるかな

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語#英語#共通テスト
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【共通テストレベル別】頻出英単語テスト60問
【1】deliver
【2】career
【3】suspect
【4】found
【5】particular
【6】quarter
【7】rumor
【8】translate
【9】polite
【10】luxury
【11】weapon
【12】fetch
【13】inherit
【14】track
【15】sequence
【16】fraglle
【17】command
【18】vocation
【19】cultivate
【20】digest
【21】sustain
【22】quote
【23】graceful
【24】subtitute
【25】dawn
【26】witness
【27】clay
【28】simultaneously
【29】intensive
【30】sacrifice
【31】descend
【32】summit
【33】in that
【34】contribute
【35】mischief
【36】gigantic
【37】overlook
【38】affirmative
【39】proclaim
【40】oath
【41】bankrupt
【42】excursion
【43】faculty
【44】orbit
【45】commence
【46】invalid
【47】perpetual
【48】segregation
【49】expenditure
【50】bestow
【51】loathe
【52】stem
【53】inquisitive
この動画を見る
【共通テストレベル別】頻出英単語テスト60問
【1】deliver
【2】career
【3】suspect
【4】found
【5】particular
【6】quarter
【7】rumor
【8】translate
【9】polite
【10】luxury
【11】weapon
【12】fetch
【13】inherit
【14】track
【15】sequence
【16】fraglle
【17】command
【18】vocation
【19】cultivate
【20】digest
【21】sustain
【22】quote
【23】graceful
【24】subtitute
【25】dawn
【26】witness
【27】clay
【28】simultaneously
【29】intensive
【30】sacrifice
【31】descend
【32】summit
【33】in that
【34】contribute
【35】mischief
【36】gigantic
【37】overlook
【38】affirmative
【39】proclaim
【40】oath
【41】bankrupt
【42】excursion
【43】faculty
【44】orbit
【45】commence
【46】invalid
【47】perpetual
【48】segregation
【49】expenditure
【50】bestow
【51】loathe
【52】stem
【53】inquisitive
〈わかるかな?〉共通テスト90点レベルの単語クイズ

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語#英語#共通テスト
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
共通テスト90点レベルの単語クイズ
①bankrupt
②excursion
③faculty
この動画を見る
共通テスト90点レベルの単語クイズ
①bankrupt
②excursion
③faculty
