 情報Ⅰ(高校生)
情報Ⅰ(高校生)
 情報Ⅰ(高校生)
情報Ⅰ(高校生)
【情報Ⅰ】pythonを使ったプログラム 複利計算やフローチャートの読み取り方と条件分岐から複利計算までの実践問題解説!

【情報Ⅰ】pythonを使ったプログラム flagやrangeを使った条件分岐と繰り返し処理を攻略!整数判定&数列プログラム問題解説

単元:
#情報Ⅰ(高校生)#プログラミング#探索と整列のプログラム
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のプログラムA、Bについて、下の問いに答えよ。
プログラムA
1 x = int(input("整数を入力"))
2 flag = False
3 for i in range(2, x):
4 if x % i == 0:
5 flag = True
6 break
7 if flag:
8 print("No")
9 else:
10 print("Yes")
プログラムB
1 a = 1
2 b = 1
3 print(a)
4 print(b)
5 for i in range(10):
6 c = a + b
7 print(c)
8 a = b
9 b = c
プログラムAについて、適当な記述を次の(ア)〜(オ)からすべて選べ。
(ア) 3を入力すると No と表示される。
(イ) 4を入力すると Yes と表示される。
(ウ) 7を入力すると Yes と表示される。
(エ) 入力された整数が素数かどうかを判定するプログラムである。
(オ) 入力された整数が偶数かどうかを判定するプログラムである。
プログラムBを実行すると、続く数字が12個表示される。数字を順番通り示したものを次の(ア)〜(エ)から一つ選べ。
(ア)
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
(イ)
1, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1
(ウ)
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144
(エ)
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144
この動画を見る
次のプログラムA、Bについて、下の問いに答えよ。
プログラムA
1 x = int(input("整数を入力"))
2 flag = False
3 for i in range(2, x):
4 if x % i == 0:
5 flag = True
6 break
7 if flag:
8 print("No")
9 else:
10 print("Yes")
プログラムB
1 a = 1
2 b = 1
3 print(a)
4 print(b)
5 for i in range(10):
6 c = a + b
7 print(c)
8 a = b
9 b = c
プログラムAについて、適当な記述を次の(ア)〜(オ)からすべて選べ。
(ア) 3を入力すると No と表示される。
(イ) 4を入力すると Yes と表示される。
(ウ) 7を入力すると Yes と表示される。
(エ) 入力された整数が素数かどうかを判定するプログラムである。
(オ) 入力された整数が偶数かどうかを判定するプログラムである。
プログラムBを実行すると、続く数字が12個表示される。数字を順番通り示したものを次の(ア)〜(エ)から一つ選べ。
(ア)
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
(イ)
1, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1
(ウ)
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144
(エ)
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144
【情報Ⅰ】pythonを使ったプログラム 絶対値と最小硬貨枚数の空欄補充問題をわかりやすく完全解説!

単元:
#情報Ⅰ(高校生)#プログラミング#探索と整列のプログラム
指導講師:
理数個別チャンネル
問題文全文(内容文):
入力された整数が変数 x に入っているとき、x の絶対値を表示する次のプログラムの空欄に適当なものを入れよ。
(1) もし ① ならば:
(2) x = ②
(3) 表示する("絶対値:", x)
商品の支払いで、50円、10円、1円の3種類の硬貨だけを使い、なるべく硬貨の枚数が少なくなるように支払いたい。
商品価格が整数 x 円のとき、支払う硬貨の最小枚数を表示する次のプログラムの空欄に適当な数字を入れよ。
(1) num50 = x ÷ ①
(2) num10 = (x − num50 × ②) ÷ ③
(3) num1 = x − num50 × ④ − num10 × ⑤
(4) 表示する("最小枚数は", num50 + num10 + num1, "枚")
この動画を見る
入力された整数が変数 x に入っているとき、x の絶対値を表示する次のプログラムの空欄に適当なものを入れよ。
(1) もし ① ならば:
(2) x = ②
(3) 表示する("絶対値:", x)
商品の支払いで、50円、10円、1円の3種類の硬貨だけを使い、なるべく硬貨の枚数が少なくなるように支払いたい。
商品価格が整数 x 円のとき、支払う硬貨の最小枚数を表示する次のプログラムの空欄に適当な数字を入れよ。
(1) num50 = x ÷ ①
(2) num10 = (x − num50 × ②) ÷ ③
(3) num1 = x − num50 × ④ − num10 × ⑤
(4) 表示する("最小枚数は", num50 + num10 + num1, "枚")
【情報Ⅰ】サイコロゲームのプログラムを解説

単元:
#情報Ⅰ(高校生)#プログラミング#アルゴリズムの表し方とプログラムの設計
指導講師:
理数個別チャンネル
問題文全文(内容文):
第3問 次の問い(問1~3)に答えよ。
問1
次の生徒(A)と生徒(B)の会話文を読み,空欄 ア・ウ に当てはまる数字を答えよ。また,空欄 イ・エ に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
A:昨日の放課後,友人Cとサイコロを使ったゲームで盛り上がったのですが,今から一緒にそのサイコロゲームをしませんか?
B:いいですね。どんなゲームなのかルールを教えてください。
A:参加プレイヤーは1つのサイコロを5回振ります。サイコロを振った際の出目(出目)が奇数(1,3,5)であれば2ポイントが得点に加算されます。サイコロの出目が偶数(2,4,6)であれば3ポイントが得点から減算されます。この作業を5回繰り返したときの最終的な得点が最も高い人の勝ちというシンプルなゲームです。
B:なるほど,シンプルなルールですね。
A:例えば,サイコロを2回振った際の出目が3,4の順である場合の得点は,奇数が1回,偶数が1回出ているので,得点は-1点となり,残り3回サイコロを振った出目が1,5,4の順に出た場合の最終的な得点は[ア]点となります。
B:得点の計算方法も理解できたので,2人で今から対決してみませんか?
A:いいですね。でも,サイコロを持っていないので,情報の授業で学習したプログラミングを使って,このゲームをパソコン上で動くようにしてみましょう。
B:そうですね。せっかく授業で学んだプログラミングの知識をここで発揮しましょう。まずは何から考えていけばよいと思いますか?
A:今回使用するサイコロの目を出力する必要があるため,関数のプログラムを作って,サイコロを再現する方法を考えましょう。以下は,乱数を使う場合の関数の説明です。
【関数の説明と例】
乱数(値)・・・0から引数として与えられた値までの範囲内で,ランダムな数値が生成され,その値が戻り値となる。
例:引数が3なら戻り値は0から3までの整数となる。
A:例えば,乱数(2)という関数を実行すると,[イ]が戻り値の候補となります。サイコロの出目は1から6なので,関数にも少し工夫が必要です。
B:サイコロの出目を再現できるようになったら,次はサイコロの出目が奇数か偶数かを判定するプログラムが必要ですね。
A:偶数か奇数かを判定する方法は,判定したい値を[ウ]で割った余りを調べるとよいですね。奇数の場合は[ウ]で割った余りが1,偶数の場合は[ウ]で割った余りが0になります。例えば,3は奇数であり,4は偶数であることが判定できます。
B:この判定を行うとると,プログラムの中で余りを計算する必要がありますが,どうしたらいいですか?
A:プログラムには色々な演算子(表1)があります。これらの演算子を利用して余りを求めることができますね。
表1 演算子の種類と使用例
| 種類 | 演算子 | 計算例 | 答え |
| 加算 | + | 1+2 | 3 |
| 減算 | - | 5-3 | 2 |
| 乗算 | × | 3×2 | 6 |
| 除算 | / | 8/2 | 4 |
| 余り | % | 7%2 | 1 |
B:例えば,2つの値を足す場合は+の演算子を使い,割り算を行う場合は[エ]の演算子を使えばいいですね。
A:その通りです。演算子を使い分けることで,さまざまな計算を行うことができます。
[イ]の解答群
⓪ 0,2 ① 1,2 ② 0,1,2 ③ 1,2,3
[エ]の解答群
⓪ + ① - ② × ③ / ④ %
問2 次の文章の空欄 オ~ケ に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
B: うーん,もう少しプログラムを作るうえでヒントが欲しいですね。全体的な流れがわかるといいのですが。
A: それでは簡単なフローチャートを考えてみましょう(図1)。サイコロゲームの流れは,サイコロを振り,出目が偶数か奇数かを判定して,得点を計算する,といった行動を5回繰り返していますね。
(図1 サイコロゲームのフローチャート)
始め
score = 0
5回繰り返す
サイコロを振る
└─ NO → scoreから3減算
└─ YES → scoreに2加算
(分岐の菱形の中:オ)
得点表示
終わり
B: フローチャートは処理の流れが可視化されて,わかりやすいですね。分岐には オ を入れればいいですね。
AさんとBさんは,これまでのヒントからプログラムを考えてみた(図2)。変数scoreには得点を求めるため初期値として0を,変数diceにはサイコロの目を求める関数を設定している。
(図2 サイコロゲームの得点を計算するプログラム)
(01) score = 0
(02) i を 1 から カ ながら繰り返す:
(03) dice = キ
(04) もし ク ならば:
(05) score = ケ + 2
(06) そうでなければ:
(07) score = ケ - 3
(08) 表示する(”得点:”, score)
オ の解答群
⓪ 出目が偶数 ① 出目が奇数 ② score が 0 ③ score が 1
カ の解答群
⓪ 5まで1ずつ増やし ① 6まで1ずつ増やし ② 5まで1ずつ減らし ③ 6まで1ずつ減らし
キ の解答群
⓪ 乱数(5) ① 乱数(6) ② 乱数(5) + 1 ③ 乱数(6) + 1
ク の解答群
⓪ dice % 2 == 0 ① dice % 2 == 1 ② score % 2 == 0 ③ score % 2 == 1
ケ の解答群
⓪ score ① dice ② i ③ i + 1
問3 次の文章を参考に,図3のプログラムの空欄【コ—シ】に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
A: プログラム(図2)が完成しました。これでサイコロゲームがコンピュータでも実行できるようになりました。
B: プログラムを動かしてみましょう。【2人でプログラムを実行してみた】
【実行結果】
Aさんの表示 得点:0
Bさんの表示 得点:5
A: きちんと動きました。Bさんの勝ちですね。もう少し白熱するようにゲームの要素を追加しませんか? 最後に特定の条件を満たした場合にボーナスポイントを与えるのはどうでしょうか?
B: いいアイデアですね。それでは,偶数の出目が5回のうち4回以上出現した場合,現在の得点に10点を追加するのはどうでしょう?
A: 最後に大逆転が起きる可能性が出てきますね。
B: そうすると,プログラムを少し改変する必要がありますね。
A: まず(02)行目に偶数の出目が出た回数をカウントするための変数 gusu を設定します。初期値には0を設定し,(09)行目には偶数の出現回数をカウントするプログラムを追加したのが,偶数の出現回数を追加したプログラム(図3)です。
(図3)
(01) score = 0
(02) gusu = 0
(03) i を 1 から 5 まで 1 ずつ増やしながら繰り返す:
(04) dice = キ
(05) もし ク ならば:
(06) score = ケ + 2
(07) そうでなければ:
(08) score = ケ - 3
(09) gusu = コ
(10) 表示する(”偶数回数:”, gusu)
(11) 表示する(”最終スコア:”, score)
B: さらに,ボーナスポイントを加算する条件を設定する必要がありますね。
【追加条件】
もし サ ならば:
score = ケ + 10
(図4 追加条件のプログラム)
A: 追加条件のプログラム(図4)は偶数の出現回数を追加したプログラム(図3)の シ 行目の下に入れると完成ですね。
生徒(A)と生徒(B)は最後にプログラムを実行したところ,正しく得点が計算されていることを確認できた。
A: プログラムを作るのは大変だけど,一度作ると繰り返し行う計算を自動化することで時間を短縮することができますね。
B: さらにルールを途中で変更できる場合,プログラムを少し改変するだけで何度も繰り返し使えると再利用性や拡張性も高いですね。情報の授業でプログラミングを学習してよかったですね。
【コ】の解答群
⓪ gusu ① gusu + 1 ② gusu + score ③ gusu + dice
【サ】の解答群
⓪ gusu > 4 ① gusu < 4 ② gusu >= 4 ③ gusu <= 4
【シ】の解答群
⓪ 3 ① 5 ② 8 ③ 9
この動画を見る
第3問 次の問い(問1~3)に答えよ。
問1
次の生徒(A)と生徒(B)の会話文を読み,空欄 ア・ウ に当てはまる数字を答えよ。また,空欄 イ・エ に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
A:昨日の放課後,友人Cとサイコロを使ったゲームで盛り上がったのですが,今から一緒にそのサイコロゲームをしませんか?
B:いいですね。どんなゲームなのかルールを教えてください。
A:参加プレイヤーは1つのサイコロを5回振ります。サイコロを振った際の出目(出目)が奇数(1,3,5)であれば2ポイントが得点に加算されます。サイコロの出目が偶数(2,4,6)であれば3ポイントが得点から減算されます。この作業を5回繰り返したときの最終的な得点が最も高い人の勝ちというシンプルなゲームです。
B:なるほど,シンプルなルールですね。
A:例えば,サイコロを2回振った際の出目が3,4の順である場合の得点は,奇数が1回,偶数が1回出ているので,得点は-1点となり,残り3回サイコロを振った出目が1,5,4の順に出た場合の最終的な得点は[ア]点となります。
B:得点の計算方法も理解できたので,2人で今から対決してみませんか?
A:いいですね。でも,サイコロを持っていないので,情報の授業で学習したプログラミングを使って,このゲームをパソコン上で動くようにしてみましょう。
B:そうですね。せっかく授業で学んだプログラミングの知識をここで発揮しましょう。まずは何から考えていけばよいと思いますか?
A:今回使用するサイコロの目を出力する必要があるため,関数のプログラムを作って,サイコロを再現する方法を考えましょう。以下は,乱数を使う場合の関数の説明です。
【関数の説明と例】
乱数(値)・・・0から引数として与えられた値までの範囲内で,ランダムな数値が生成され,その値が戻り値となる。
例:引数が3なら戻り値は0から3までの整数となる。
A:例えば,乱数(2)という関数を実行すると,[イ]が戻り値の候補となります。サイコロの出目は1から6なので,関数にも少し工夫が必要です。
B:サイコロの出目を再現できるようになったら,次はサイコロの出目が奇数か偶数かを判定するプログラムが必要ですね。
A:偶数か奇数かを判定する方法は,判定したい値を[ウ]で割った余りを調べるとよいですね。奇数の場合は[ウ]で割った余りが1,偶数の場合は[ウ]で割った余りが0になります。例えば,3は奇数であり,4は偶数であることが判定できます。
B:この判定を行うとると,プログラムの中で余りを計算する必要がありますが,どうしたらいいですか?
A:プログラムには色々な演算子(表1)があります。これらの演算子を利用して余りを求めることができますね。
表1 演算子の種類と使用例
| 種類 | 演算子 | 計算例 | 答え |
| 加算 | + | 1+2 | 3 |
| 減算 | - | 5-3 | 2 |
| 乗算 | × | 3×2 | 6 |
| 除算 | / | 8/2 | 4 |
| 余り | % | 7%2 | 1 |
B:例えば,2つの値を足す場合は+の演算子を使い,割り算を行う場合は[エ]の演算子を使えばいいですね。
A:その通りです。演算子を使い分けることで,さまざまな計算を行うことができます。
[イ]の解答群
⓪ 0,2 ① 1,2 ② 0,1,2 ③ 1,2,3
[エ]の解答群
⓪ + ① - ② × ③ / ④ %
問2 次の文章の空欄 オ~ケ に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
B: うーん,もう少しプログラムを作るうえでヒントが欲しいですね。全体的な流れがわかるといいのですが。
A: それでは簡単なフローチャートを考えてみましょう(図1)。サイコロゲームの流れは,サイコロを振り,出目が偶数か奇数かを判定して,得点を計算する,といった行動を5回繰り返していますね。
(図1 サイコロゲームのフローチャート)
始め
score = 0
5回繰り返す
サイコロを振る
└─ NO → scoreから3減算
└─ YES → scoreに2加算
(分岐の菱形の中:オ)
得点表示
終わり
B: フローチャートは処理の流れが可視化されて,わかりやすいですね。分岐には オ を入れればいいですね。
AさんとBさんは,これまでのヒントからプログラムを考えてみた(図2)。変数scoreには得点を求めるため初期値として0を,変数diceにはサイコロの目を求める関数を設定している。
(図2 サイコロゲームの得点を計算するプログラム)
(01) score = 0
(02) i を 1 から カ ながら繰り返す:
(03) dice = キ
(04) もし ク ならば:
(05) score = ケ + 2
(06) そうでなければ:
(07) score = ケ - 3
(08) 表示する(”得点:”, score)
オ の解答群
⓪ 出目が偶数 ① 出目が奇数 ② score が 0 ③ score が 1
カ の解答群
⓪ 5まで1ずつ増やし ① 6まで1ずつ増やし ② 5まで1ずつ減らし ③ 6まで1ずつ減らし
キ の解答群
⓪ 乱数(5) ① 乱数(6) ② 乱数(5) + 1 ③ 乱数(6) + 1
ク の解答群
⓪ dice % 2 == 0 ① dice % 2 == 1 ② score % 2 == 0 ③ score % 2 == 1
ケ の解答群
⓪ score ① dice ② i ③ i + 1
問3 次の文章を参考に,図3のプログラムの空欄【コ—シ】に入れるのに最も適当なものを,後の解答群のうちから一つずつ選べ。
A: プログラム(図2)が完成しました。これでサイコロゲームがコンピュータでも実行できるようになりました。
B: プログラムを動かしてみましょう。【2人でプログラムを実行してみた】
【実行結果】
Aさんの表示 得点:0
Bさんの表示 得点:5
A: きちんと動きました。Bさんの勝ちですね。もう少し白熱するようにゲームの要素を追加しませんか? 最後に特定の条件を満たした場合にボーナスポイントを与えるのはどうでしょうか?
B: いいアイデアですね。それでは,偶数の出目が5回のうち4回以上出現した場合,現在の得点に10点を追加するのはどうでしょう?
A: 最後に大逆転が起きる可能性が出てきますね。
B: そうすると,プログラムを少し改変する必要がありますね。
A: まず(02)行目に偶数の出目が出た回数をカウントするための変数 gusu を設定します。初期値には0を設定し,(09)行目には偶数の出現回数をカウントするプログラムを追加したのが,偶数の出現回数を追加したプログラム(図3)です。
(図3)
(01) score = 0
(02) gusu = 0
(03) i を 1 から 5 まで 1 ずつ増やしながら繰り返す:
(04) dice = キ
(05) もし ク ならば:
(06) score = ケ + 2
(07) そうでなければ:
(08) score = ケ - 3
(09) gusu = コ
(10) 表示する(”偶数回数:”, gusu)
(11) 表示する(”最終スコア:”, score)
B: さらに,ボーナスポイントを加算する条件を設定する必要がありますね。
【追加条件】
もし サ ならば:
score = ケ + 10
(図4 追加条件のプログラム)
A: 追加条件のプログラム(図4)は偶数の出現回数を追加したプログラム(図3)の シ 行目の下に入れると完成ですね。
生徒(A)と生徒(B)は最後にプログラムを実行したところ,正しく得点が計算されていることを確認できた。
A: プログラムを作るのは大変だけど,一度作ると繰り返し行う計算を自動化することで時間を短縮することができますね。
B: さらにルールを途中で変更できる場合,プログラムを少し改変するだけで何度も繰り返し使えると再利用性や拡張性も高いですね。情報の授業でプログラミングを学習してよかったですね。
【コ】の解答群
⓪ gusu ① gusu + 1 ② gusu + score ③ gusu + dice
【サ】の解答群
⓪ gusu > 4 ① gusu < 4 ② gusu >= 4 ③ gusu <= 4
【シ】の解答群
⓪ 3 ① 5 ② 8 ③ 9
【情報Ⅰ】最小硬貨枚数を計算するプログラムを解説

単元:
#情報Ⅰ(高校生)#プログラミング#アルゴリズムの表し方とプログラムの設計
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の生徒(S)と先生(T)の会話文を読み、空欄〔ア〕に当てはまる数字をマークせよ。
また、空欄〔イ〕〜〔エ〕に入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。ただし、空欄〔ウ〕・〔エ〕は解答の順序は問わない
S:この前、お客さんが460円の商品を買うのに、510円を払って、釣り銭を50円受け取っていたのを見て、授業で勉強したプログラミングで、そんな「上手な払い方」を計算するプログラムを作ってみたいなと思いました。
T:いいですね。「上手な払い方」とは何を考える必要がありますね。
S:普通は手持ちの硬貨の枚数を少なくするような払い方でしょうか。
T:そうですね。ただ、ここでは、客が支払う枚数と釣り銭を受け取る枚数の合計を最小にする払い方を考えてみませんか?客も店も十分な枚数の効果を持っていると仮定しましょう。計算を簡単にするために、100円以下の買い物とし、使う硬貨は1円玉、5円玉、10円玉、50円玉、100円玉のみで500円玉は使わない場合を考えてみましょう。
例えば、46円をちょうど支払う場合、支払い枚数はどうなりますか?
S:46円を支払うには、10円玉4枚、5円玉1枚、1円玉1枚という6枚で払い方が最小の枚数になります。
T:そうですね。一方、同じ46円を支払うのに、51円を支払って釣り銭5円受け取る払い方では、支払いに2枚、釣り銭に1枚で、合計3枚の硬貨のやりとりになります。こうすると交換する硬貨の枚数の合計が最小になりますね。
S:これが上手な払い方ですね。
T:そうです。このように、客と店員が交換する硬貨の合計が最小となる枚数、すなわち「最小交換硬貨枚数」の計算を考えましょう。
S:どうやって考えればいいかなぁ。
T:ここでは、次の関数のプログラムを作り、それを使う方法を考えてみましょう。目標の金額を釣り銭無くちょうど支払うために必要な最小の硬貨枚数を求める関数です。
【関数の説明と例】
枚数(金額)…引数として「金額」が与えられ、ちょうどその金額となる硬貨の組合せの中で、枚数が最小となる硬貨枚数が戻り値となる関数。
例:8円は「5円玉が1枚と1円玉が3枚」の組合せで最小の硬貨枚数になるので、枚数(8)の値は4となる。
これは、例えば、枚数(46)=〔ア〕 と計算してくれるような関数です。これを使って最小交換硬貨枚数の計算を考えてみましょう。例えば、46円を支払うのに、51円払って5円の釣り銭を受け取る払い方をした場合、客と店員の間で交換される硬貨枚数の合計は、この関数を使うと、どのように計算できますか?
S:〔イ〕で求められますね。
T:一般に、商品の価格x円に対して釣り銭y円を0,1,2,・・・と変化させて、それぞれの場合に必要な硬貨の枚数の合計を
枚数(〔ウ〕)+枚数(〔エ〕)と計算し、一番小さな値を最小交換硬貨枚数とすればよいのです。
S:なるほど。それで、釣り銭yはいくらまで調べればよいでしょうか?
T:面白い数字パズルですね。まあ、詳しくは今度考えるとして、今回は100円以下の商品なのでyは99まで調べれば十分でしょう。
【イの解答群】
⓪ 枚数(51)+枚数(5)
① 枚数(46)+枚数(5)
② 枚数(51)−枚数(5)
③ 枚数(46)−枚数(5)
【ウ・エの解答群】
⓪ x
① y
② x+y
③ x−y
問2
次の文章の空欄〔オ〕〜〔コ〕に入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。
S:まずは、関数「枚数(金額)」のプログラムを作るために、与えられた金額ちょうどになる最小の硬貨枚数を計算するプログラムを考えてみます。もう少しヒントが欲しいなぁ。
T:金額に対して、高額の硬貨から使うように考えて枚数と残金を計算していくとよいでしょう。また、金額に対して、ある額の硬貨が何枚まで使えて、残金がいくらになるかを計算するには、整数値の商を求める演算「÷」とその余りを求める演算「%」が使えるでしょう。例えば、46円に対して10円玉が何枚まで使えるかは〔オ〕で、その際にいくら残るかは〔カ〕で求めることができますね。
S:なるほど!あとは自分でできそうです。
Sさんは、先生(T)との会話からヒントを得て、変数 kingaku に与えられた目標の金額(100円以下)に対し、その金額ちょうどになる最小の硬貨枚数を計算するプログラムを考えてみた(図1)。ここでは例として目標の金額を46円としている。
配列 kouka に硬貨の単位を小さい順に設定している。なお、配列の添え字は0から始まるものとする。最低額の硬貨が1円玉なのでkouka[0]の値は1となる。
先生(T)のヒントに従い、高額の硬貨から何枚まで使えるかを計算する方針で、(4)〜(6)行目のような繰り返し文にした。この繰り返しで、変数 maisu に支払う硬貨の枚数の合計が計算され、変数 nokori に残りいくら支払えればよいか、という残金が計算される。
実行してみると〔ア〕が表示されたので、正しく計算できていることが分かる。いろいろな例で試してみたが、すべて正しく計算できていることを確認できた。
(図1)目標の金額ちょうどになる最小の硬貨枚数を計算するプログラム
(1) kouka = [1,5,10,50,100]
(2) kingaku = 46
(3) maisu = 0, nokori = kingaku
(4) 〔i〕を 〔キ〕 ながら繰り返す:
(5) maisu = 〔ク〕 + 〔ケ〕
(6) nokori = 〔コ〕
(7) 表示する(maisu)
【オ・カの解答群】
⓪ 46 ÷ 10 + 1
① 46 % 10 − 1
② 46 ÷ 10
③ 46 % 10
【キの解答群】
⓪ 5から1まで1ずつ減らし
① 4から0まで1ずつ減らし
② 0から4まで1ずつ増やし
③ 1から5まで1ずつ増やし
【クの解答群】
⓪ 1
① maisu
② i
③ nokori
【ケ・コの解答群】
⓪ nokori ÷ Kouka[i]
① nokori % Kouka[i]
② maisu ÷ Kouka[i]
③ maisu % Kouka[i]
問3
次の文章を参考に、図2のプログラムの空欄〔サ〕〜〔タ〕に入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。ただし、空欄〔ス〕・〔セ〕は解答の順序は問わない。
T:プログラム(図1)ができたようですね。それを使えば、関数「枚数(金額)」のプログラムができます。関数の引数として与えられる金額の値をプログラム(図1)の変数 kingaku に設定し、(7)行目の代わりに変数 maisu の値を関数の戻り値とすれば、関数「枚数(金額)」のプログラムとなります。では、その関数を使って最小交換硬貨枚数を計算するプログラムを作ってみましょう。ここでも、100円以下の買い物として考えてみます。
【関数の説明(再掲)】
枚数(金額)…引数として「金額」が与えられ、ちょうどその金額となる硬貨の組合せの中で、枚数が最小となる硬貨枚数が戻り値となる関数。
Sさんは、図2のようなプログラムを作成した。変数 kakaku に与えられる商品の価格に対して、釣り銭を変数 tsuri を用意し、妥当な tsuri のすべての値に対して交換する硬貨の枚数を調べ、その最小値を求めるプログラムである。なお、ここでは例として商品の価格を46円としている。
このプログラムでは、先生(T)のアドバイスに従い、釣り銭無しの場合も含め、99円までのすべての釣り銭に対し、その釣り銭になるように支払う場合に交換される硬貨の枚数を求め、その最小値を最小交換硬貨枚数として計算している。
最小値の計算では、これまでの払い方での最小枚数を変数 min_maisu に記憶しておき、それより少ない枚数の払い方が出るたびに更新している。min_maisuの初期値には、十分大きな値として100を用いている。100円以下の買い物では、使う硬貨の枚数は100枚を超えないからである。
(図2)最小交換硬貨枚数を求めるプログラム
(1) kakaku = 46
(2) min_maisu = 100
(3) 〔サ〕を 〔ジ〕 から 99 まで1ずつ増やしながら繰り返す:
(4) shiharai = kakaku + tsuri
(5) maisu = 〔ス〕 + 〔セ〕
(6) もし 〔ソ〕 < min_maisu ならば:
(7) 〔タ〕 = 〔ソ〕
(8) 表示する(min_maisu)
このプログラムを実行してみたところ3が表示された。46円を支払うときの最小交換硬貨枚数は、支払いで50円玉が1枚、1円玉が1枚、釣り銭で5円玉が1枚の計3枚なので、正しく計算できていることが分かる。同様に、kakaku の値をいろいろと変えて実行してみたところ、すべて正しく計算できていることを確認できた。
【サ・ソ・タの解答群】
⓪ maisu
① min_maisu
② shiharai
③ tsuri
【シの解答群】
⓪ 0
① 1
② 99
③ 100
【ス・セの解答群】
⓪ 枚数(shiharai)
① 枚数(kakaku)
② 枚数(tsuri)
③ shiharai
④ kakaku
⑤ tsuri
この動画を見る
次の生徒(S)と先生(T)の会話文を読み、空欄〔ア〕に当てはまる数字をマークせよ。
また、空欄〔イ〕〜〔エ〕に入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。ただし、空欄〔ウ〕・〔エ〕は解答の順序は問わない
S:この前、お客さんが460円の商品を買うのに、510円を払って、釣り銭を50円受け取っていたのを見て、授業で勉強したプログラミングで、そんな「上手な払い方」を計算するプログラムを作ってみたいなと思いました。
T:いいですね。「上手な払い方」とは何を考える必要がありますね。
S:普通は手持ちの硬貨の枚数を少なくするような払い方でしょうか。
T:そうですね。ただ、ここでは、客が支払う枚数と釣り銭を受け取る枚数の合計を最小にする払い方を考えてみませんか?客も店も十分な枚数の効果を持っていると仮定しましょう。計算を簡単にするために、100円以下の買い物とし、使う硬貨は1円玉、5円玉、10円玉、50円玉、100円玉のみで500円玉は使わない場合を考えてみましょう。
例えば、46円をちょうど支払う場合、支払い枚数はどうなりますか?
S:46円を支払うには、10円玉4枚、5円玉1枚、1円玉1枚という6枚で払い方が最小の枚数になります。
T:そうですね。一方、同じ46円を支払うのに、51円を支払って釣り銭5円受け取る払い方では、支払いに2枚、釣り銭に1枚で、合計3枚の硬貨のやりとりになります。こうすると交換する硬貨の枚数の合計が最小になりますね。
S:これが上手な払い方ですね。
T:そうです。このように、客と店員が交換する硬貨の合計が最小となる枚数、すなわち「最小交換硬貨枚数」の計算を考えましょう。
S:どうやって考えればいいかなぁ。
T:ここでは、次の関数のプログラムを作り、それを使う方法を考えてみましょう。目標の金額を釣り銭無くちょうど支払うために必要な最小の硬貨枚数を求める関数です。
【関数の説明と例】
枚数(金額)…引数として「金額」が与えられ、ちょうどその金額となる硬貨の組合せの中で、枚数が最小となる硬貨枚数が戻り値となる関数。
例:8円は「5円玉が1枚と1円玉が3枚」の組合せで最小の硬貨枚数になるので、枚数(8)の値は4となる。
これは、例えば、枚数(46)=〔ア〕 と計算してくれるような関数です。これを使って最小交換硬貨枚数の計算を考えてみましょう。例えば、46円を支払うのに、51円払って5円の釣り銭を受け取る払い方をした場合、客と店員の間で交換される硬貨枚数の合計は、この関数を使うと、どのように計算できますか?
S:〔イ〕で求められますね。
T:一般に、商品の価格x円に対して釣り銭y円を0,1,2,・・・と変化させて、それぞれの場合に必要な硬貨の枚数の合計を
枚数(〔ウ〕)+枚数(〔エ〕)と計算し、一番小さな値を最小交換硬貨枚数とすればよいのです。
S:なるほど。それで、釣り銭yはいくらまで調べればよいでしょうか?
T:面白い数字パズルですね。まあ、詳しくは今度考えるとして、今回は100円以下の商品なのでyは99まで調べれば十分でしょう。
【イの解答群】
⓪ 枚数(51)+枚数(5)
① 枚数(46)+枚数(5)
② 枚数(51)−枚数(5)
③ 枚数(46)−枚数(5)
【ウ・エの解答群】
⓪ x
① y
② x+y
③ x−y
問2
次の文章の空欄〔オ〕〜〔コ〕に入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。
S:まずは、関数「枚数(金額)」のプログラムを作るために、与えられた金額ちょうどになる最小の硬貨枚数を計算するプログラムを考えてみます。もう少しヒントが欲しいなぁ。
T:金額に対して、高額の硬貨から使うように考えて枚数と残金を計算していくとよいでしょう。また、金額に対して、ある額の硬貨が何枚まで使えて、残金がいくらになるかを計算するには、整数値の商を求める演算「÷」とその余りを求める演算「%」が使えるでしょう。例えば、46円に対して10円玉が何枚まで使えるかは〔オ〕で、その際にいくら残るかは〔カ〕で求めることができますね。
S:なるほど!あとは自分でできそうです。
Sさんは、先生(T)との会話からヒントを得て、変数 kingaku に与えられた目標の金額(100円以下)に対し、その金額ちょうどになる最小の硬貨枚数を計算するプログラムを考えてみた(図1)。ここでは例として目標の金額を46円としている。
配列 kouka に硬貨の単位を小さい順に設定している。なお、配列の添え字は0から始まるものとする。最低額の硬貨が1円玉なのでkouka[0]の値は1となる。
先生(T)のヒントに従い、高額の硬貨から何枚まで使えるかを計算する方針で、(4)〜(6)行目のような繰り返し文にした。この繰り返しで、変数 maisu に支払う硬貨の枚数の合計が計算され、変数 nokori に残りいくら支払えればよいか、という残金が計算される。
実行してみると〔ア〕が表示されたので、正しく計算できていることが分かる。いろいろな例で試してみたが、すべて正しく計算できていることを確認できた。
(図1)目標の金額ちょうどになる最小の硬貨枚数を計算するプログラム
(1) kouka = [1,5,10,50,100]
(2) kingaku = 46
(3) maisu = 0, nokori = kingaku
(4) 〔i〕を 〔キ〕 ながら繰り返す:
(5) maisu = 〔ク〕 + 〔ケ〕
(6) nokori = 〔コ〕
(7) 表示する(maisu)
【オ・カの解答群】
⓪ 46 ÷ 10 + 1
① 46 % 10 − 1
② 46 ÷ 10
③ 46 % 10
【キの解答群】
⓪ 5から1まで1ずつ減らし
① 4から0まで1ずつ減らし
② 0から4まで1ずつ増やし
③ 1から5まで1ずつ増やし
【クの解答群】
⓪ 1
① maisu
② i
③ nokori
【ケ・コの解答群】
⓪ nokori ÷ Kouka[i]
① nokori % Kouka[i]
② maisu ÷ Kouka[i]
③ maisu % Kouka[i]
問3
次の文章を参考に、図2のプログラムの空欄〔サ〕〜〔タ〕に入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。ただし、空欄〔ス〕・〔セ〕は解答の順序は問わない。
T:プログラム(図1)ができたようですね。それを使えば、関数「枚数(金額)」のプログラムができます。関数の引数として与えられる金額の値をプログラム(図1)の変数 kingaku に設定し、(7)行目の代わりに変数 maisu の値を関数の戻り値とすれば、関数「枚数(金額)」のプログラムとなります。では、その関数を使って最小交換硬貨枚数を計算するプログラムを作ってみましょう。ここでも、100円以下の買い物として考えてみます。
【関数の説明(再掲)】
枚数(金額)…引数として「金額」が与えられ、ちょうどその金額となる硬貨の組合せの中で、枚数が最小となる硬貨枚数が戻り値となる関数。
Sさんは、図2のようなプログラムを作成した。変数 kakaku に与えられる商品の価格に対して、釣り銭を変数 tsuri を用意し、妥当な tsuri のすべての値に対して交換する硬貨の枚数を調べ、その最小値を求めるプログラムである。なお、ここでは例として商品の価格を46円としている。
このプログラムでは、先生(T)のアドバイスに従い、釣り銭無しの場合も含め、99円までのすべての釣り銭に対し、その釣り銭になるように支払う場合に交換される硬貨の枚数を求め、その最小値を最小交換硬貨枚数として計算している。
最小値の計算では、これまでの払い方での最小枚数を変数 min_maisu に記憶しておき、それより少ない枚数の払い方が出るたびに更新している。min_maisuの初期値には、十分大きな値として100を用いている。100円以下の買い物では、使う硬貨の枚数は100枚を超えないからである。
(図2)最小交換硬貨枚数を求めるプログラム
(1) kakaku = 46
(2) min_maisu = 100
(3) 〔サ〕を 〔ジ〕 から 99 まで1ずつ増やしながら繰り返す:
(4) shiharai = kakaku + tsuri
(5) maisu = 〔ス〕 + 〔セ〕
(6) もし 〔ソ〕 < min_maisu ならば:
(7) 〔タ〕 = 〔ソ〕
(8) 表示する(min_maisu)
このプログラムを実行してみたところ3が表示された。46円を支払うときの最小交換硬貨枚数は、支払いで50円玉が1枚、1円玉が1枚、釣り銭で5円玉が1枚の計3枚なので、正しく計算できていることが分かる。同様に、kakaku の値をいろいろと変えて実行してみたところ、すべて正しく計算できていることを確認できた。
【サ・ソ・タの解答群】
⓪ maisu
① min_maisu
② shiharai
③ tsuri
【シの解答群】
⓪ 0
① 1
② 99
③ 100
【ス・セの解答群】
⓪ 枚数(shiharai)
① 枚数(kakaku)
② 枚数(tsuri)
③ shiharai
④ kakaku
⑤ tsuri
【共通テスト模試解説】情報:問4 浮動小数点数の表現

単元:
#情報Ⅰ(高校生)#模試解説・過去問解説#デジタル#デジタル化された情報とその表し方
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の太郎さんと先生の会話文を読み、空欄【ク】〜【シ】に入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。
太郎:コンピュータのメモリにも制限がありますよね。大きな数や絶対値の小さな数を計算するのにも制約があると思うのですが、どうやって計算しているのでしょうか。
先生:浮動小数点数を用いて計算を工夫する方法があります。
太郎:それはどんな方法ですか?
先生:わかりやすく10進法で表現した数の場合から説明すると、例えば、
123000000 を 1.23 × 10【ク】と表します。
太郎:なるほど、それなら大きな数や絶対値の小さな数を扱いやすくなりますね。
2進法で表現した数の場合でも同じように計算するのですか?
先生:2進法で表現した数の場合はもう少し工夫します。実際に、次のような約束があります。
米国電気電子学会(IEEE)によって規格化された浮動小数点数の表現法では、
総ビット数 32 の場合、符号を S(1ビット)、指数部を E(8ビット)、仮数部を M(23ビット)として
(-1)^S × 1.M × 2^E-127
となるように表す。
太郎:難しそうですね。
先生:具体例で考えましょう。なお、数の末尾の (2) は2進法で表現した数であることを示します。
S = 0
E = 1000 0000 (2)
M = 100 0000 0000 0000 0000 0000 (2)
となる10進法で表現した数はわかりますか?
太郎:E = 1000 0000 (2) = 128 なので、
(−1)^0×1.1(2)×2^128−127=11(2)=【ケ】
ですね。
先生:正解です。では、−1792 = −111 0000 0000(2) で表される数の S, E, M はわかりますか?
太郎:えっと、同じように考えると
S = 【コ】
E = 【サ】(2)
M = 【シ】0000 0000 0000 0000 0000 (2)
ですね。
先生:そのとおりです。
【解答群】
ク の解答群
[0] 6 [1] 7 [2] 8 [3] 9 [4] 10
ケ の解答群
[0] 0 [1] 1 [2] 2 [3] 3 [4] 4 [5] 5
コ の解答群
[0] 0 [1] 1
サ の解答群
[0] 1000 0011 [1] 1000 0101 [2] 1000 1001 [3] 1000 1011 [4] 1000 1101 [5] 1000 1111
シ の解答群
[0] 100 [1] 101 [2] 110 [3] 111
この動画を見る
次の太郎さんと先生の会話文を読み、空欄【ク】〜【シ】に入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。
太郎:コンピュータのメモリにも制限がありますよね。大きな数や絶対値の小さな数を計算するのにも制約があると思うのですが、どうやって計算しているのでしょうか。
先生:浮動小数点数を用いて計算を工夫する方法があります。
太郎:それはどんな方法ですか?
先生:わかりやすく10進法で表現した数の場合から説明すると、例えば、
123000000 を 1.23 × 10【ク】と表します。
太郎:なるほど、それなら大きな数や絶対値の小さな数を扱いやすくなりますね。
2進法で表現した数の場合でも同じように計算するのですか?
先生:2進法で表現した数の場合はもう少し工夫します。実際に、次のような約束があります。
米国電気電子学会(IEEE)によって規格化された浮動小数点数の表現法では、
総ビット数 32 の場合、符号を S(1ビット)、指数部を E(8ビット)、仮数部を M(23ビット)として
(-1)^S × 1.M × 2^E-127
となるように表す。
太郎:難しそうですね。
先生:具体例で考えましょう。なお、数の末尾の (2) は2進法で表現した数であることを示します。
S = 0
E = 1000 0000 (2)
M = 100 0000 0000 0000 0000 0000 (2)
となる10進法で表現した数はわかりますか?
太郎:E = 1000 0000 (2) = 128 なので、
(−1)^0×1.1(2)×2^128−127=11(2)=【ケ】
ですね。
先生:正解です。では、−1792 = −111 0000 0000(2) で表される数の S, E, M はわかりますか?
太郎:えっと、同じように考えると
S = 【コ】
E = 【サ】(2)
M = 【シ】0000 0000 0000 0000 0000 (2)
ですね。
先生:そのとおりです。
【解答群】
ク の解答群
[0] 6 [1] 7 [2] 8 [3] 9 [4] 10
ケ の解答群
[0] 0 [1] 1 [2] 2 [3] 3 [4] 4 [5] 5
コ の解答群
[0] 0 [1] 1
サ の解答群
[0] 1000 0011 [1] 1000 0101 [2] 1000 1001 [3] 1000 1011 [4] 1000 1101 [5] 1000 1111
シ の解答群
[0] 100 [1] 101 [2] 110 [3] 111
【情報Ⅰ】大学入学共通テスト対応プログラム表記で学ぶ!条件分岐の基礎からくじ引きプログラムまで解説

単元:
#情報Ⅰ(高校生)#プログラミング#アルゴリズムの表し方とプログラムの設計
指導講師:
理数個別チャンネル
問題文全文(内容文):
問1 次の文章を読み、空欄ア〜キに入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。
生徒:今度の文化祭でくじ引き大会をすることになりました。せっかくなので、くじ引きプログラミングを作りたいのですが、何から始めたらいいんですか。
先生:それはいいですね! まずは、大学入学共通テスト用のプログラム表記を使って条件分岐から学んでいきましょう。
例えば、正六面体のサイコロを振って3が出たら「当たり!」と表示し、それ以外なら「はずれ」と表示されるプログラムは次のようになります。
(01) saikoro = 3 # サイコロの出目
(02) もし ア ならば:
(03) 表示する(“当たり!”)
(04) そうでなければ:
(05) 表示する(“はずれ”)
生徒:なるほど! サイコロの出目が1なら「1等」、2〜3なら「2等」、それ以外なら「はずれ」と表示するのは、次のようになりますね。
(01) saikoro = 3 # サイコロの出目
(02) もし イ ならば:
(03) 表示する(“1等”)
(04) そうでなくもし ウ ならば:
(05) 表示する(“2等”)
(06) そうでなければ:
(07) 表示する(“はずれ”)
ア・イ・ウの解答群
| 0 saikoro == 0 | 1 saikoro == 1 | 2 saikoro == 2 |
| 3 saikoro == 3 | 4 saikoro <= 3 | 5 saikoro <= 3 |
| 6 saikoro > 3 | 7 saikoro < 3 |
先生:その通り。このままだと1行目の変数saikoroの値を手入力する必要があるので、乱数を使うといいですね。次の乱数関数を使っていきましょう。
f 乱数の説明
乱数(n)…0から引数として与えられた整数の中からランダムに1つ返却する。
生徒:ということは,1行目を以下のように変更すればよいですね。
(01) saikoro = エ
エ の解答群
| 0 乱数(6) | 1 乱数(5) | 2 乱数(6)+1 | 3 乱数(5)+1 |
先生:その通り。では今度は配列を使って景品を表示するプログラムを作成していきましょう。サイコロの目の数に対応するように配列Keihinを作成します。はずれの場合も,アメを渡すとしましょう。
配列名:Keihin プラモ ポテチ チョコ アメ アメ アメ
このとき添字が0から始まるとした場合,先頭から数えて3番目のチョコの要素を取り出したい場合は以下のように記述すればいいですね。
item = オ
オ の解答群
| 0 Keihin+3 | 1 Keihin[3] | 2 Keihin[2] | 3 Keihin[0] |
先生:実際はサイコロの目と対応しているので,景品を表示する場合は9行目のように記述します。
(01) Keihin = ["プラモ","ポテチ","チョコ","アメ","アメ","アメ"]
(02) saikoro = エ # サイコロの出目
(03) もし イ ならば:
(04) 表示する(“1等”)
(05) そうでなくもし ウ ならば:
(06) 表示する(“2等”)
(07) そうでなければ:
(08) 表示する(“はずれ”)
(09) 表示する(“景品:”, カ)
カ の解答群
| 0 Keihin[saikoro] | 1 Keihin[saikoro-1] | 2 Keihin[1] | 3 Keihin[saikoro+1] |
生徒:完成しましたね! ただ、一人3回くじを引かせたいです。
先生:それなら、処理全体を繰り返し文で囲むといいですね。3行目の処理で、何回目のくじ引きかも表示するようにしましょう。
(01) Keihin = ["プラモ","ポテチ","チョコ","アメ","アメ","アメ"]
(02) i を キ
(03) 表示する(i+1,"回目")
(04) saikoro = エ # サイコロの出目
(05) もし イ ならば:
(06) 表示する(“1等”)
(07) そうでなくもし ウ ならば:
(08) 表示する(“2等”)
(09) そうでなければ:
(10) 表示する(“はずれ”)
(11) 表示する(“景品:”, カ)
キ の解答群
| 0 0から2まで1ずつ増やしながら繰り返す |
| 1 0から3まで1ずつ増やしながら繰り返す |
| 2 2から6まで1ずつ減らしながら繰り返す |
| 3 1から3まで1ずつ増やしながら繰り返す |
生徒:ループの中に条件分岐があると難しく感じますが、1つ1つを順番に作っていったので理解できました!
先生:大学入学共通テストの「情報Ⅰ」でも、このように入れ子構造で出題される可能性があります。いきなり全体を見ると難しく感じますが、処理の内容を1つ1つ押さえて、この構造に慣れていきましょう。
この動画を見る
問1 次の文章を読み、空欄ア〜キに入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。
生徒:今度の文化祭でくじ引き大会をすることになりました。せっかくなので、くじ引きプログラミングを作りたいのですが、何から始めたらいいんですか。
先生:それはいいですね! まずは、大学入学共通テスト用のプログラム表記を使って条件分岐から学んでいきましょう。
例えば、正六面体のサイコロを振って3が出たら「当たり!」と表示し、それ以外なら「はずれ」と表示されるプログラムは次のようになります。
(01) saikoro = 3 # サイコロの出目
(02) もし ア ならば:
(03) 表示する(“当たり!”)
(04) そうでなければ:
(05) 表示する(“はずれ”)
生徒:なるほど! サイコロの出目が1なら「1等」、2〜3なら「2等」、それ以外なら「はずれ」と表示するのは、次のようになりますね。
(01) saikoro = 3 # サイコロの出目
(02) もし イ ならば:
(03) 表示する(“1等”)
(04) そうでなくもし ウ ならば:
(05) 表示する(“2等”)
(06) そうでなければ:
(07) 表示する(“はずれ”)
ア・イ・ウの解答群
| 0 saikoro == 0 | 1 saikoro == 1 | 2 saikoro == 2 |
| 3 saikoro == 3 | 4 saikoro <= 3 | 5 saikoro <= 3 |
| 6 saikoro > 3 | 7 saikoro < 3 |
先生:その通り。このままだと1行目の変数saikoroの値を手入力する必要があるので、乱数を使うといいですね。次の乱数関数を使っていきましょう。
f 乱数の説明
乱数(n)…0から引数として与えられた整数の中からランダムに1つ返却する。
生徒:ということは,1行目を以下のように変更すればよいですね。
(01) saikoro = エ
エ の解答群
| 0 乱数(6) | 1 乱数(5) | 2 乱数(6)+1 | 3 乱数(5)+1 |
先生:その通り。では今度は配列を使って景品を表示するプログラムを作成していきましょう。サイコロの目の数に対応するように配列Keihinを作成します。はずれの場合も,アメを渡すとしましょう。
配列名:Keihin プラモ ポテチ チョコ アメ アメ アメ
このとき添字が0から始まるとした場合,先頭から数えて3番目のチョコの要素を取り出したい場合は以下のように記述すればいいですね。
item = オ
オ の解答群
| 0 Keihin+3 | 1 Keihin[3] | 2 Keihin[2] | 3 Keihin[0] |
先生:実際はサイコロの目と対応しているので,景品を表示する場合は9行目のように記述します。
(01) Keihin = ["プラモ","ポテチ","チョコ","アメ","アメ","アメ"]
(02) saikoro = エ # サイコロの出目
(03) もし イ ならば:
(04) 表示する(“1等”)
(05) そうでなくもし ウ ならば:
(06) 表示する(“2等”)
(07) そうでなければ:
(08) 表示する(“はずれ”)
(09) 表示する(“景品:”, カ)
カ の解答群
| 0 Keihin[saikoro] | 1 Keihin[saikoro-1] | 2 Keihin[1] | 3 Keihin[saikoro+1] |
生徒:完成しましたね! ただ、一人3回くじを引かせたいです。
先生:それなら、処理全体を繰り返し文で囲むといいですね。3行目の処理で、何回目のくじ引きかも表示するようにしましょう。
(01) Keihin = ["プラモ","ポテチ","チョコ","アメ","アメ","アメ"]
(02) i を キ
(03) 表示する(i+1,"回目")
(04) saikoro = エ # サイコロの出目
(05) もし イ ならば:
(06) 表示する(“1等”)
(07) そうでなくもし ウ ならば:
(08) 表示する(“2等”)
(09) そうでなければ:
(10) 表示する(“はずれ”)
(11) 表示する(“景品:”, カ)
キ の解答群
| 0 0から2まで1ずつ増やしながら繰り返す |
| 1 0から3まで1ずつ増やしながら繰り返す |
| 2 2から6まで1ずつ減らしながら繰り返す |
| 3 1から3まで1ずつ増やしながら繰り返す |
生徒:ループの中に条件分岐があると難しく感じますが、1つ1つを順番に作っていったので理解できました!
先生:大学入学共通テストの「情報Ⅰ」でも、このように入れ子構造で出題される可能性があります。いきなり全体を見ると難しく感じますが、処理の内容を1つ1つ押さえて、この構造に慣れていきましょう。
【情報Ⅰ】シフト暗号のプログラムの問題解説

単元:
#情報Ⅰ(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師:
理数個別チャンネル
問題文全文(内容文):
第5問 次の文章を読み、後の問い(問1〜3)に答えよ。
シフト暗号はアルファベットの文字を決まった文字数分シフトさせて(ずらして)置き換える極めて単純な暗号手段である。
TさんとMさんは授業で先生が出した課題であるシフト暗号で暗号化した暗号文をいかに解読するかを考えることにした
問1 次の会話文を読み、空欄【アイ】~【キク】に当てはまる数字をマークせよ。
課題 英文をシフト暗号で暗号化した以下の暗号文を解読しなさい。ただし、英文字は全て小
文字でアルファベット以外のスペースや数字,「!」,「?」などは変換されていません。
(省略)... nonsmkdo k zybdsxy yp drkd psvon, kc k pskvk bodcsaxq zvkmo pyb
ydrc gory boqa dkfo drosb vsfo drkd ok xdkys wsgxr4 vsfo. sd sc kydaydorb
psdssdxa ksn zbyob yrdkd go crven ny drsc. led, sd vkqabo coxco, eo mkx xyd
nonsmkdo - go mkx xyd myxcombkdo - go mkx xyd rvkvvg - drsc qbyexn. dro lbkfo
wox, vsfsax kxn nokn, gry cdbeqavon robo, rkfo myxcombkdon sd, pkb k lfyfo yeb
zyyb zygob dy knn yb nodbkmd. dro gybvn gsvv vsdvod xydo, xyb vyxq bowowlob
grkd go cki robo, led sd mkx xofob pybqod grkd droi nsn robo. sd ....(省略)
Mさん:シフト暗号って,例えばアルファベットを5文字右にシフトした場合,文字「a」は文字
「f」に,文字「x」はまず2文字シフトして右端に達した後一番左端に戻り3文字シフ
トした文字「c」に置き換わるやつだよね。暗号化された文字列の復号は,その逆,つまり
左に5文字シフトすればできるよね。
Tさん:復号は必ずしも反対にシフトする必要はないよね。例えば9文字右にシフトされていた場合,
復号するには9文字左にシフトしても良いけど,右に【アイ】文字シフトすることもできるね。
図2のようにアルファベットに0〜25の番号を割り当てて考えてみると,暗号化してx番目の文字になった時,
復号はx+【アイ】の値が【ウエ】以下であればx+【アイ】番の文字に置き換わるけど,【ウエ】より大きい場合は,x+【アイ】−【オカ】番の文字に置き換えれば復号できるよね。
Mさん:暗号化で文字を何文字シフトしているか分かれば、この復号法で解読できるよね。どうやったら分かるかな。
Tさん:すべての可能性、つまり【キク】通りをプログラムで試せばいいんじゃない?
Mさん:この場合だと【キク】通りで済むけども、大文字があったり、
日本語のように文字種の数が多い言語ではとても効率が悪い方法だよ。英語であれば、単語によって文字「e」が人気があるし、逆に「z」が含まれる単語はあまり思いつかないよね。アルファベットの出現頻度を調べていればある程度推測できるんじゃないかな。インターネットで調べてみようよ。
Mさん:どうやら一般的な英文のアルファベットの出現頻度には図3のような傾向があるみたいだよ。
Tさん:文字によって出現頻度に特徴がある。暗号化された英文のアルファベットの出現頻度を調べれば、
何文字シフトされているか推測することができそうだね。1つ〜数え上げるのは大変だから数え上げるプログラムを考えてみるよ。
問2 次の会話文を読み,空欄【ケ】【コ】に当てはまる内容を,後の解答群のうちから一つずつ選べ。また,空欄【サ】に当てはまる数字をマークせよ。
Tさん:暗号化された英文のアルファベットの出現頻度を数え上げるプログラムを図5のように考えてみたよ。このプログラムでは,配列変数Angoubunに暗号文を入れて,一文字ずつアルファベットの出現頻度を数え上げて,その結果を配列変数Hindoに入れているんだ。
Hindo[0] が a,Hindo[25] が z に対応しているよ。
(01) Angoubun = ["p","y","e","b",…(省略)…"k","b","d","r","."]
(02) 配列Hindoのすべての要素に0を代入する
(03) i を 0 から 要素数(Angoubun)-1 まで1ずつ増やしながら:
(04) | bangou = 差分 【ケ】
(05) | もし bangou != -1 ならば:
(06) | 【コ】 = 【コ】 +1
(07) | 表示する(Hindo)
【関数の説明】
要素数(値)…配列の要素数を返す。
例:Data =["M","i","s","s","i","s","s","i","p","p","i"] の時
要素数(Data) は11を返す
差分(値)…アルファベットの「a」との位置の差分を返す
値がアルファベット以外の文字であれば−1を返す
例:差分("e") は4を、差分("x") は23を返す
差分("5") や 差分(",") は−1を返す
Mさん:これでアルファベットの出現頻度が調べられるよね。それで結果はどうなったの?
Tさん:このプログラムで得られた配列Hindoをグラフ化してみたよ(図6)。
Mさん:このアルファベットの出現頻度を見ると,「o」「d」「k」「y」が多いね。逆に出現頻度が
少ない「a」「h」「j」「t」も手掛かりになるね。図3と照らし合わせると,この暗号化さ
れた文字列は右に【サシ】文字シフトしていると考えられるね。
Tさん:うん,でもそれが正しいか,実際にプログラムを作って復号してみようよ。
ケ・コの解答群
| 0 Angoubun[i] | 1 Angoubun[i−1] | 2 Angoubun[bangou] |
| 3 Angoubun[bangou−1] | 4 Hindo[bangou] | 5 Hindo[bangou−1] |
| 6 Hindo[i] | 7 Hindo[i−1] |
問3 次の会話文の空欄【ス】〜【チ】に当てはまる内容を,後の解答群のうちから一つずつ選べ。
Tさん:暗号文を一文字ずつ復号して表示するプログラムができたよ(図7)。
Mさん:なるほど、復号も右にシフトで考えればいいんだね。実行してみたら読める英文になったの?
(01) Angoubun = ["p","y","e","b",…(省略)… "k","b","d","r","."]
(02) 配列変数 Hirabun を初期化する
(03) hukugosuu = 26 - 10
(04) i を 0 から 要素数(Angoubun)-1 まで1ずつ増やしながら:
(05) | bangou = 差分(Angoubun[i])
(06) | もし 0 <= bangou + 【ス】 <= 25 ならば:
(07) | Hirabun[i] = 文字( bangou + 【ス】 )
(08) | そうでなければ:
(09) | Hirabun[i] = 文字( bangou + 【セ】 )
(10) | L Hirabun[i] = 文字( 【ソ】 )
(11) そうでなければ:
(12) | L Hirabun[i] = Hirabun[i]
(13) 表示する(Hirabun)
図7 暗号文を復号するプログラム
Mさん:これって有名なリンカーンのゲティスバーグ演説じゃない。ほら最後のところ有名なフレーズだよね。
Tさん:先生、課題ができました。元の英文はリンカーンのゲティスバーグ演説ですね。プログラムで文字の出現頻度を調べて、シフトされた文字数を推測しました。復号はこのプログラムで変換してみました。
先生:よくできたね。素晴らしい!このプログラムはもっと簡単にできるね。この⑦〜⑩の部分が式は工夫すれば1行にまとめられるよ。ヒントは余りを求める算術演算子%を使うんだ。
Tさん:えっ,1行ですか? …分かった!
Hirabun[i] = 文字(【タ】 % 【チ】)
とすればもっと簡潔にできたんだ。
先生:素晴らしい!
ス〜ソ の解答群
| 0 bangou+hukugousuu | 1 bangou |
| 2 hukugousuu | 3 bangou+hukugousuu−26 |
| 4 hukugousuu−25 | 5 hukugousuu−26 |
| 6 Angoubun[i] | 7 Hirabun[i] |
| 8 Angoubun[i+hukugousuu] |
タ の解答群
| 0 bangou+hukugousuu | 1 (bangou+hukugousuu) |
| 2 hukugousuu | 3 (bangou+hukugousuu−26) |
| 4 hukugousuu+26 | 5 (hukugousuu+26) |
チ の解答群
| 0 25 | 1 26 | 2 bangou | 3 hukugousuu |
この動画を見る
第5問 次の文章を読み、後の問い(問1〜3)に答えよ。
シフト暗号はアルファベットの文字を決まった文字数分シフトさせて(ずらして)置き換える極めて単純な暗号手段である。
TさんとMさんは授業で先生が出した課題であるシフト暗号で暗号化した暗号文をいかに解読するかを考えることにした
問1 次の会話文を読み、空欄【アイ】~【キク】に当てはまる数字をマークせよ。
課題 英文をシフト暗号で暗号化した以下の暗号文を解読しなさい。ただし、英文字は全て小
文字でアルファベット以外のスペースや数字,「!」,「?」などは変換されていません。
(省略)... nonsmkdo k zybdsxy yp drkd psvon, kc k pskvk bodcsaxq zvkmo pyb
ydrc gory boqa dkfo drosb vsfo drkd ok xdkys wsgxr4 vsfo. sd sc kydaydorb
psdssdxa ksn zbyob yrdkd go crven ny drsc. led, sd vkqabo coxco, eo mkx xyd
nonsmkdo - go mkx xyd myxcombkdo - go mkx xyd rvkvvg - drsc qbyexn. dro lbkfo
wox, vsfsax kxn nokn, gry cdbeqavon robo, rkfo myxcombkdon sd, pkb k lfyfo yeb
zyyb zygob dy knn yb nodbkmd. dro gybvn gsvv vsdvod xydo, xyb vyxq bowowlob
grkd go cki robo, led sd mkx xofob pybqod grkd droi nsn robo. sd ....(省略)
Mさん:シフト暗号って,例えばアルファベットを5文字右にシフトした場合,文字「a」は文字
「f」に,文字「x」はまず2文字シフトして右端に達した後一番左端に戻り3文字シフ
トした文字「c」に置き換わるやつだよね。暗号化された文字列の復号は,その逆,つまり
左に5文字シフトすればできるよね。
Tさん:復号は必ずしも反対にシフトする必要はないよね。例えば9文字右にシフトされていた場合,
復号するには9文字左にシフトしても良いけど,右に【アイ】文字シフトすることもできるね。
図2のようにアルファベットに0〜25の番号を割り当てて考えてみると,暗号化してx番目の文字になった時,
復号はx+【アイ】の値が【ウエ】以下であればx+【アイ】番の文字に置き換わるけど,【ウエ】より大きい場合は,x+【アイ】−【オカ】番の文字に置き換えれば復号できるよね。
Mさん:暗号化で文字を何文字シフトしているか分かれば、この復号法で解読できるよね。どうやったら分かるかな。
Tさん:すべての可能性、つまり【キク】通りをプログラムで試せばいいんじゃない?
Mさん:この場合だと【キク】通りで済むけども、大文字があったり、
日本語のように文字種の数が多い言語ではとても効率が悪い方法だよ。英語であれば、単語によって文字「e」が人気があるし、逆に「z」が含まれる単語はあまり思いつかないよね。アルファベットの出現頻度を調べていればある程度推測できるんじゃないかな。インターネットで調べてみようよ。
Mさん:どうやら一般的な英文のアルファベットの出現頻度には図3のような傾向があるみたいだよ。
Tさん:文字によって出現頻度に特徴がある。暗号化された英文のアルファベットの出現頻度を調べれば、
何文字シフトされているか推測することができそうだね。1つ〜数え上げるのは大変だから数え上げるプログラムを考えてみるよ。
問2 次の会話文を読み,空欄【ケ】【コ】に当てはまる内容を,後の解答群のうちから一つずつ選べ。また,空欄【サ】に当てはまる数字をマークせよ。
Tさん:暗号化された英文のアルファベットの出現頻度を数え上げるプログラムを図5のように考えてみたよ。このプログラムでは,配列変数Angoubunに暗号文を入れて,一文字ずつアルファベットの出現頻度を数え上げて,その結果を配列変数Hindoに入れているんだ。
Hindo[0] が a,Hindo[25] が z に対応しているよ。
(01) Angoubun = ["p","y","e","b",…(省略)…"k","b","d","r","."]
(02) 配列Hindoのすべての要素に0を代入する
(03) i を 0 から 要素数(Angoubun)-1 まで1ずつ増やしながら:
(04) | bangou = 差分 【ケ】
(05) | もし bangou != -1 ならば:
(06) | 【コ】 = 【コ】 +1
(07) | 表示する(Hindo)
【関数の説明】
要素数(値)…配列の要素数を返す。
例:Data =["M","i","s","s","i","s","s","i","p","p","i"] の時
要素数(Data) は11を返す
差分(値)…アルファベットの「a」との位置の差分を返す
値がアルファベット以外の文字であれば−1を返す
例:差分("e") は4を、差分("x") は23を返す
差分("5") や 差分(",") は−1を返す
Mさん:これでアルファベットの出現頻度が調べられるよね。それで結果はどうなったの?
Tさん:このプログラムで得られた配列Hindoをグラフ化してみたよ(図6)。
Mさん:このアルファベットの出現頻度を見ると,「o」「d」「k」「y」が多いね。逆に出現頻度が
少ない「a」「h」「j」「t」も手掛かりになるね。図3と照らし合わせると,この暗号化さ
れた文字列は右に【サシ】文字シフトしていると考えられるね。
Tさん:うん,でもそれが正しいか,実際にプログラムを作って復号してみようよ。
ケ・コの解答群
| 0 Angoubun[i] | 1 Angoubun[i−1] | 2 Angoubun[bangou] |
| 3 Angoubun[bangou−1] | 4 Hindo[bangou] | 5 Hindo[bangou−1] |
| 6 Hindo[i] | 7 Hindo[i−1] |
問3 次の会話文の空欄【ス】〜【チ】に当てはまる内容を,後の解答群のうちから一つずつ選べ。
Tさん:暗号文を一文字ずつ復号して表示するプログラムができたよ(図7)。
Mさん:なるほど、復号も右にシフトで考えればいいんだね。実行してみたら読める英文になったの?
(01) Angoubun = ["p","y","e","b",…(省略)… "k","b","d","r","."]
(02) 配列変数 Hirabun を初期化する
(03) hukugosuu = 26 - 10
(04) i を 0 から 要素数(Angoubun)-1 まで1ずつ増やしながら:
(05) | bangou = 差分(Angoubun[i])
(06) | もし 0 <= bangou + 【ス】 <= 25 ならば:
(07) | Hirabun[i] = 文字( bangou + 【ス】 )
(08) | そうでなければ:
(09) | Hirabun[i] = 文字( bangou + 【セ】 )
(10) | L Hirabun[i] = 文字( 【ソ】 )
(11) そうでなければ:
(12) | L Hirabun[i] = Hirabun[i]
(13) 表示する(Hirabun)
図7 暗号文を復号するプログラム
Mさん:これって有名なリンカーンのゲティスバーグ演説じゃない。ほら最後のところ有名なフレーズだよね。
Tさん:先生、課題ができました。元の英文はリンカーンのゲティスバーグ演説ですね。プログラムで文字の出現頻度を調べて、シフトされた文字数を推測しました。復号はこのプログラムで変換してみました。
先生:よくできたね。素晴らしい!このプログラムはもっと簡単にできるね。この⑦〜⑩の部分が式は工夫すれば1行にまとめられるよ。ヒントは余りを求める算術演算子%を使うんだ。
Tさん:えっ,1行ですか? …分かった!
Hirabun[i] = 文字(【タ】 % 【チ】)
とすればもっと簡潔にできたんだ。
先生:素晴らしい!
ス〜ソ の解答群
| 0 bangou+hukugousuu | 1 bangou |
| 2 hukugousuu | 3 bangou+hukugousuu−26 |
| 4 hukugousuu−25 | 5 hukugousuu−26 |
| 6 Angoubun[i] | 7 Hirabun[i] |
| 8 Angoubun[i+hukugousuu] |
タ の解答群
| 0 bangou+hukugousuu | 1 (bangou+hukugousuu) |
| 2 hukugousuu | 3 (bangou+hukugousuu−26) |
| 4 hukugousuu+26 | 5 (hukugousuu+26) |
チ の解答群
| 0 25 | 1 26 | 2 bangou | 3 hukugousuu |
2025年5月実施共通テスト模試「情報Ⅰ」大問3解説!

単元:
#情報Ⅰ(高校生)#プログラミング#アルゴリズムの表し方とプログラムの設計#探索と整列のプログラム#プログラムによる動的シミュレーション
指導講師:
理数個別チャンネル
問題文全文(内容文):
2025年5月実施共通テスト模試「情報Ⅰ」大問3解説!
この動画を見る
2025年5月実施共通テスト模試「情報Ⅰ」大問3解説!
予備校講師のストライキはありなのか【賛否両論大揉め中】

単元:
#大学入試過去問(数学)#情報Ⅰ(高校生)#全統模試(河合塾)#英語(高校生)#大学入試過去問(英語)#全統模試(河合塾)#数学(高校生)#模試解説・過去問解説#【河合塾】全統共通テスト模試
指導講師:
Morite2 English Channel
問題文全文(内容文):
緊急速報!予備校業界を揺るがすストライキ騒動で、人気講師が炎上する事態に!
YouTubeチャンネル「Morite2 English Channel」で、河合塾講師による異例のストライキに関する動画が投稿され、大きな波紋を呼んでいる。今回の騒動では、人気予備校講師である荻野(おぎの)先生が、SNS(X)へのある投稿をきっかけに「炎上」してしまった!
荻野先生は、「生徒に迷惑をかけたらダメ」という、予備校講師や生徒の立場からすれば当然とも言える意見を投稿した。しかしこれに対し、多くの社会人や労働者の目線を持つ人々から、「ストライキは迷惑をかけなきゃ意味がない」といった批判が殺到したのだ。ストライキは本来、労働者の権利であり、雇用主に圧力をかけるために消費者側に迷惑がかかるのが目的だという考え方だ。
これは、教育業界の「予備校講師目線」と、一般的な「労働者目線」という、全く異なる立場の意見が激しく衝突した結果だ。教育業界では、ストライキはすべきではないという観念があるため、そもそもストライキを考えたこともない講師が多い。
今回のストライキは、ベテラン講師のコマ単価が長年変わらず、若手講師の賃金も低いという労働問題が背景にある。しかし、ベテラン講師から見て「安い」と感じる年収(500〜600万円程度)でも、若手から見れば「高い」と感じられるため、世代間で意見の対立が生まれている。
ストライキをした講師は、後輩の若い世代のためにも声を上げている可能性がある。しかし、予備校講師は業務委託契約が多く、会社員と違って簡単に契約を切られるリスクがあるため、ストライキをするにはそれなりの覚悟が必要だと指摘されている。
森鉄先生は、荻野先生と同じく「自分ならストライキはしない」としつつも、「する権利はある」という見解を示している。日本では、人に迷惑をかけないことを前提とする文化があるため、今回の行動は「日本の文化を逸脱した」と捉える人もいるのではないかと分析されている。
このストライキ論争は、「日本の予備校講師は労働者なのか?」「教育にストライキは許されるのか?」という根本的な問題を投げかけている。
この激しい議論の行方から、目が離せない!
この動画を見る
緊急速報!予備校業界を揺るがすストライキ騒動で、人気講師が炎上する事態に!
YouTubeチャンネル「Morite2 English Channel」で、河合塾講師による異例のストライキに関する動画が投稿され、大きな波紋を呼んでいる。今回の騒動では、人気予備校講師である荻野(おぎの)先生が、SNS(X)へのある投稿をきっかけに「炎上」してしまった!
荻野先生は、「生徒に迷惑をかけたらダメ」という、予備校講師や生徒の立場からすれば当然とも言える意見を投稿した。しかしこれに対し、多くの社会人や労働者の目線を持つ人々から、「ストライキは迷惑をかけなきゃ意味がない」といった批判が殺到したのだ。ストライキは本来、労働者の権利であり、雇用主に圧力をかけるために消費者側に迷惑がかかるのが目的だという考え方だ。
これは、教育業界の「予備校講師目線」と、一般的な「労働者目線」という、全く異なる立場の意見が激しく衝突した結果だ。教育業界では、ストライキはすべきではないという観念があるため、そもそもストライキを考えたこともない講師が多い。
今回のストライキは、ベテラン講師のコマ単価が長年変わらず、若手講師の賃金も低いという労働問題が背景にある。しかし、ベテラン講師から見て「安い」と感じる年収(500〜600万円程度)でも、若手から見れば「高い」と感じられるため、世代間で意見の対立が生まれている。
ストライキをした講師は、後輩の若い世代のためにも声を上げている可能性がある。しかし、予備校講師は業務委託契約が多く、会社員と違って簡単に契約を切られるリスクがあるため、ストライキをするにはそれなりの覚悟が必要だと指摘されている。
森鉄先生は、荻野先生と同じく「自分ならストライキはしない」としつつも、「する権利はある」という見解を示している。日本では、人に迷惑をかけないことを前提とする文化があるため、今回の行動は「日本の文化を逸脱した」と捉える人もいるのではないかと分析されている。
このストライキ論争は、「日本の予備校講師は労働者なのか?」「教育にストライキは許されるのか?」という根本的な問題を投げかけている。
この激しい議論の行方から、目が離せない!
河合塾講師のストで荻野先生が炎上 #shorts

単元:
#大学入試過去問(数学)#情報Ⅰ(高校生)#全統模試(河合塾)#英語(高校生)#大学入試過去問(英語)#全統模試(河合塾)#数学(高校生)#模試解説・過去問解説#【河合塾】全統共通テスト模試
指導講師:
Morite2 English Channel
問題文全文(内容文):
緊急速報!河合塾講師のストライキ問題が飛び火!なぜかあの予備校講師が**炎上**する事態に!
人気YouTubeチャンネル「Morite2 English Channel」が、先日投稿した**塾講師のストライキ動画**に寄せられたコメントが波紋を呼んでいる。なんと、予備校の**荻野(おぎの)先生**が「炎上」しているというのだ!
炎上のきっかけは、荻野先生がSNS(X)で「**生徒に迷惑をかけたらダメ**」と投稿したこと。生徒にとっては授業をしないことは迷惑がかかる、という予備校講師目線、生徒目線からの当然の意見だった。授業が中断されれば進度が遅れる可能性もあるからだ。
ところがこれに対し、「**ストライキは迷惑をかけなきゃ意味がない**」といったコメントが殺到!労働者として生きる社会人から見れば、消費者側に迷惑がかかるのが「スト」なのだ、という意見がぶつけられた形だ。
荻野先生からすると、「あんたたちの目線で予備校や教育業界を語るな」ということだろう。これは、予備校講師目線と、労働者(社会人)目線という、**目線が全く違う**ために、折り合いがつくわけがない状況だという。
この動画では、交渉や条件という意味を持つ重要な単語「**terms**」について、「**come to terms**(折り合いがつく)」という形で出題されやすいと解説し、受験生への学習アドバイスも添えられている。
このストライキ論争、あなたはどちらの意見に共感する?予備校業界を揺るがす議論から目が離せない!
この動画を見る
緊急速報!河合塾講師のストライキ問題が飛び火!なぜかあの予備校講師が**炎上**する事態に!
人気YouTubeチャンネル「Morite2 English Channel」が、先日投稿した**塾講師のストライキ動画**に寄せられたコメントが波紋を呼んでいる。なんと、予備校の**荻野(おぎの)先生**が「炎上」しているというのだ!
炎上のきっかけは、荻野先生がSNS(X)で「**生徒に迷惑をかけたらダメ**」と投稿したこと。生徒にとっては授業をしないことは迷惑がかかる、という予備校講師目線、生徒目線からの当然の意見だった。授業が中断されれば進度が遅れる可能性もあるからだ。
ところがこれに対し、「**ストライキは迷惑をかけなきゃ意味がない**」といったコメントが殺到!労働者として生きる社会人から見れば、消費者側に迷惑がかかるのが「スト」なのだ、という意見がぶつけられた形だ。
荻野先生からすると、「あんたたちの目線で予備校や教育業界を語るな」ということだろう。これは、予備校講師目線と、労働者(社会人)目線という、**目線が全く違う**ために、折り合いがつくわけがない状況だという。
この動画では、交渉や条件という意味を持つ重要な単語「**terms**」について、「**come to terms**(折り合いがつく)」という形で出題されやすいと解説し、受験生への学習アドバイスも添えられている。
このストライキ論争、あなたはどちらの意見に共感する?予備校業界を揺るがす議論から目が離せない!
河合塾で初のストライキ【元講師が詳細解説】

単元:
#大学入試過去問(数学)#情報Ⅰ(高校生)#全統模試(河合塾)#英語(高校生)#大学入試過去問(英語)#全統模試(河合塾)#数学(高校生)#模試解説・過去問解説#【河合塾】全統共通テスト模試
指導講師:
Morite2 English Channel
問題文全文(内容文):
大手の河合塾で異例の**ストライキ**が発生!元講師がその詳細を解説する激震の内容だ!
予備校・学習塾業界で大手としては**初めて**となる授業中のストライキが実施された! 今回ストライキを決行したのは、河合塾ユニオンの委員長で、物理を担当する竹達さん(講師歴38年目のベテラン)だという。ストライキは授業全てではなく、90分間の授業の**最後の15分間**に限定して行われる予定だ!
ストライキの背景には、ベテラン講師の**コマ単価が10年以上変わっていない**現状がある。竹達委員長は、コマ単価が約1万7,000円という状況が続き、年収は約500万円から600万円程度だと明かしている。時給に換算すると1万円を超えると見ることもできるが、コマがなければ生活できない、安定しない職業であり、会社からの手当も少ないため、これを高いと取るか低いと取るかは人によると述べられている。
ユニオン側が要求しているのは主に3点だ。
1. **賃上げの実現**:1分あたり35円(1コマ90分で3,150円)の賃上げ。これは時給換算で2,100円の賃上げとなり、この業界では「強欲な申し出」とも聞こえるが、講師は授業準備や採点、生徒の質問対応、保護者への連絡などの業務を無給で行っており、長時間拘束されている点を訴えている。
2. **私学共済への加入**:業務委託契約の講師でも私学共済に加入できるようにすること。
3. **無期転換権の承認**:業務委託契約の講師にも5年間で無期転換を認めるよう要求。
ユニオン側は、物価高騰で実質賃金が下がる中、賃上げ要求を河合塾に一蹴されたため、今回のストライキを決行したとしている。
委員長は、「生徒に迷惑をかけたくない」という思いから授業の最後の15分間に限定したストを実施。ストライキは労働者の基本的な権利であり、業界の多くの場所で若者が疲弊している現状を見て、**「塾講師も労働者である」**ことを示すために、あえて最も象徴的な「スト」の権利を発揮し、他の塾講師がストライキを起こす際のハードルを下げる狙いがあるという。
これに対し河合塾側は、「要求項目に対する弊方の見解が理解いただけず残念」としつつも、適法に行われるストライキは受け入れ、**別の講師による補填授業**(90分間まるまる授業)を用意することで対応するとしている。
この慰霊のストライキが、予備校業界の労働環境をどう変えるのか、結果に注目が集まっている!
この動画を見る
大手の河合塾で異例の**ストライキ**が発生!元講師がその詳細を解説する激震の内容だ!
予備校・学習塾業界で大手としては**初めて**となる授業中のストライキが実施された! 今回ストライキを決行したのは、河合塾ユニオンの委員長で、物理を担当する竹達さん(講師歴38年目のベテラン)だという。ストライキは授業全てではなく、90分間の授業の**最後の15分間**に限定して行われる予定だ!
ストライキの背景には、ベテラン講師の**コマ単価が10年以上変わっていない**現状がある。竹達委員長は、コマ単価が約1万7,000円という状況が続き、年収は約500万円から600万円程度だと明かしている。時給に換算すると1万円を超えると見ることもできるが、コマがなければ生活できない、安定しない職業であり、会社からの手当も少ないため、これを高いと取るか低いと取るかは人によると述べられている。
ユニオン側が要求しているのは主に3点だ。
1. **賃上げの実現**:1分あたり35円(1コマ90分で3,150円)の賃上げ。これは時給換算で2,100円の賃上げとなり、この業界では「強欲な申し出」とも聞こえるが、講師は授業準備や採点、生徒の質問対応、保護者への連絡などの業務を無給で行っており、長時間拘束されている点を訴えている。
2. **私学共済への加入**:業務委託契約の講師でも私学共済に加入できるようにすること。
3. **無期転換権の承認**:業務委託契約の講師にも5年間で無期転換を認めるよう要求。
ユニオン側は、物価高騰で実質賃金が下がる中、賃上げ要求を河合塾に一蹴されたため、今回のストライキを決行したとしている。
委員長は、「生徒に迷惑をかけたくない」という思いから授業の最後の15分間に限定したストを実施。ストライキは労働者の基本的な権利であり、業界の多くの場所で若者が疲弊している現状を見て、**「塾講師も労働者である」**ことを示すために、あえて最も象徴的な「スト」の権利を発揮し、他の塾講師がストライキを起こす際のハードルを下げる狙いがあるという。
これに対し河合塾側は、「要求項目に対する弊方の見解が理解いただけず残念」としつつも、適法に行われるストライキは受け入れ、**別の講師による補填授業**(90分間まるまる授業)を用意することで対応するとしている。
この慰霊のストライキが、予備校業界の労働環境をどう変えるのか、結果に注目が集まっている!
223 公開鍵暗号方式の基本を解説:暗号化の流れを体感しよう! #shorts

単元:
#情報Ⅰ(高校生)#ネットワーク#さまざまな情報システム#安全のための対策と技術
指導講師:
めいちゃんねる
問題文全文(内容文):
一般的な公開鍵暗号方式では、鍵を作成するのは送信者である、マルかバツか。
この動画を見る
一般的な公開鍵暗号方式では、鍵を作成するのは送信者である、マルかバツか。
共通テスト頑張った人に、今伝えたいこと

単元:
#大学入試過去問(数学)#物理#化学#生物#情報Ⅰ(高校生)#センター試験・共通テスト関連#共通テスト#大学入試過去問(物理)#大学入試過去問(化学)#英語(高校生)#国語(高校生)#社会(高校生)#日本史#世界史#大学入試過去問(英語)#大学入試過去問(国語)#共通テスト#共通テスト(現代文)#大学入試過去問(生物)#共通テスト・センター試験#共通テスト(古文)#共通テスト#大学入試過去問・共通テスト・模試関連#大学入試過去問・共通テスト・模試関連#数学(高校生)#理科(高校生)#共通テスト#模試解説・過去問解説#【河合塾】全統共通テスト模試
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
この動画を見る
共通テストで絶望した人の溜まり場【カサニマロ ライブ】

単元:
#大学入試過去問(数学)#物理#化学#生物#情報Ⅰ(高校生)#センター試験・共通テスト関連#共通テスト#大学入試過去問(物理)#大学入試過去問(化学)#英語(高校生)#国語(高校生)#社会(高校生)#日本史#世界史#大学入試過去問(英語)#大学入試過去問(国語)#共通テスト#共通テスト(現代文)#大学入試過去問(生物)#共通テスト・センター試験#共通テスト(古文)#共通テスト#大学入試過去問・共通テスト・模試関連#大学入試過去問・共通テスト・模試関連#数学(高校生)#理科(高校生)#共通テスト#模試解説・過去問解説#【河合塾】全統共通テスト模試
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
この動画を見る
共通テストを終えて_全部難しかったよ

単元:
#大学入試過去問(数学)#物理#化学#生物#情報Ⅰ(高校生)#センター試験・共通テスト関連#共通テスト#大学入試過去問(物理)#大学入試過去問(化学)#英語(高校生)#国語(高校生)#社会(高校生)#日本史#世界史#大学入試過去問(英語)#大学入試過去問(国語)#共通テスト#共通テスト(現代文)#大学入試過去問(生物)#共通テスト・センター試験#共通テスト(古文)#共通テスト#大学入試過去問・共通テスト・模試関連#大学入試過去問・共通テスト・模試関連#数学(高校生)#理科(高校生)#共通テスト#模試解説・過去問解説#【河合塾】全統共通テスト模試
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
この動画を見る
共通テスト2日目_ふきふき占い【午後も頑張れ】

単元:
#大学入試過去問(数学)#物理#化学#生物#情報Ⅰ(高校生)#センター試験・共通テスト関連#共通テスト#大学入試過去問(物理)#大学入試過去問(化学)#英語(高校生)#国語(高校生)#社会(高校生)#日本史#世界史#大学入試過去問(英語)#大学入試過去問(国語)#共通テスト#共通テスト(現代文)#大学入試過去問(生物)#共通テスト・センター試験#共通テスト(古文)#共通テスト#大学入試過去問・共通テスト・模試関連#大学入試過去問・共通テスト・模試関連#数学(高校生)#理科(高校生)#共通テスト#模試解説・過去問解説#【河合塾】全統共通テスト模試
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
この動画を見る
共通テスト2日目で上手くいくコツ、伝えます

単元:
#情報Ⅰ(高校生)#大学入試解答速報#数学#共通テスト#英語#化学#物理#共通テスト#共通テスト#共通テスト#世界史#共通テスト#模試解説・過去問解説#【河合塾】全統共通テスト模試
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
この動画を見る
【共通テスト】情報Ⅰを解くときのコツまとめ7選

単元:
#情報Ⅰ(高校生)#その他#勉強法#その他
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
【共通テスト】情報Ⅰを解くときのコツまとめ7選を解説していきます。
この動画を見る
【共通テスト】情報Ⅰを解くときのコツまとめ7選を解説していきます。
330 待ち行列:シミュレーションの定番問題に挑戦!
単元:
#情報Ⅰ(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師:
めいちゃんねる
問題文全文(内容文):
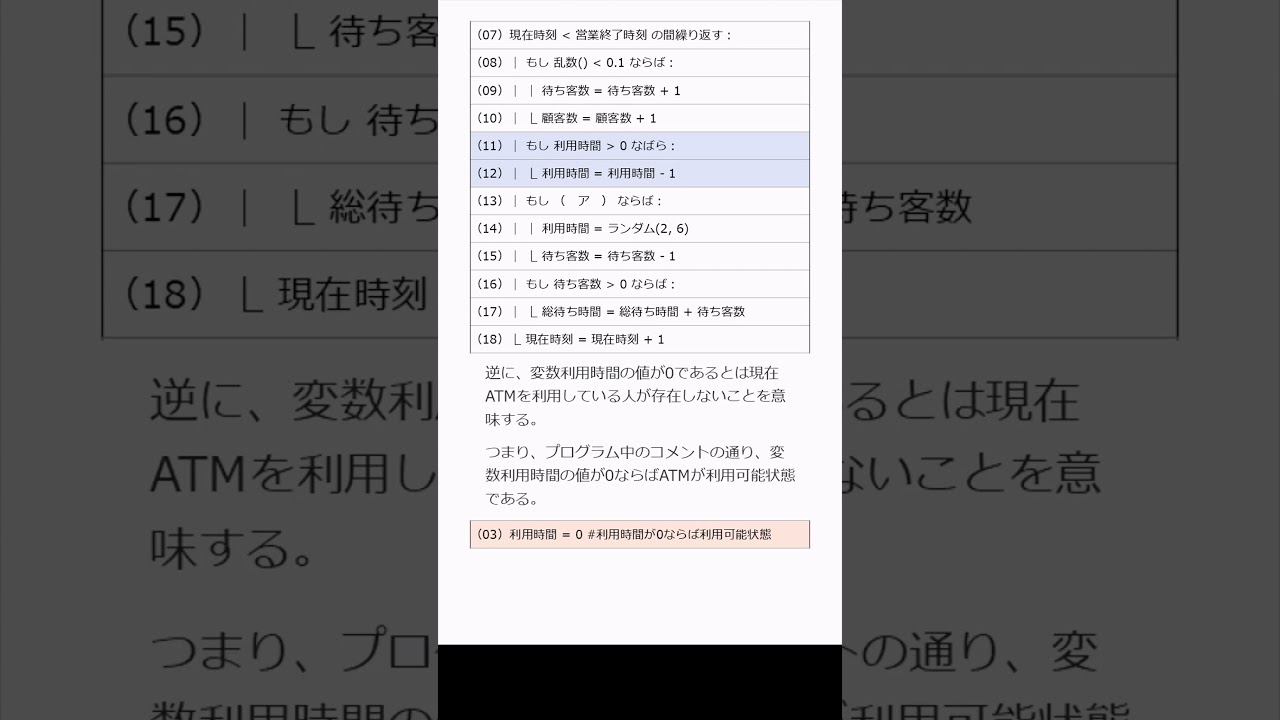
次のプログラムはあるコンビニに設置された1台のATMの平均待ち時間についてのシミュレーションである。
このATMの作動時間は1日900分である。
顧客は毎分0.1の確率で訪れる。
顧客一人あたりのATM利用時間は2分から6分のランダムな時間である。
乱数は0以上1未満の実数を返す関数であり、ランダム整数(n, m)はnからmの整数をランダムに返す関数である。
空欄に入る最も適切なものを選べ。
この動画を見る
次のプログラムはあるコンビニに設置された1台のATMの平均待ち時間についてのシミュレーションである。
このATMの作動時間は1日900分である。
顧客は毎分0.1の確率で訪れる。
顧客一人あたりのATM利用時間は2分から6分のランダムな時間である。
乱数は0以上1未満の実数を返す関数であり、ランダム整数(n, m)はnからmの整数をランダムに返す関数である。
空欄に入る最も適切なものを選べ。
【情報Ⅰ】共通テスト試作問題【第3問プログラミング解説】問題PDFもあるよ!
328 ランダムウォーク:予測できない未来を推定する

単元:
#情報Ⅰ(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師:
めいちゃんねる
問題文全文(内容文):
このプログラムはxy平面上を動く点をプロットするものである。 動く点は、各繰り返しごとにx軸方向に0.1、y軸方向に+1または-1だけ動く。 y軸方向に+1動くか-1動くかはランダムである。 乱数は0以上1未満の実数をランダムに返す関数であり、要素追加(配列, 値)は配列の末尾に新しい要素を追加する関数である。 また、プロットする(配列X, 配列Y)は2つの配列の同じ添字の要素を組みとして、xy平面に座標をプロットして表示する関数である。 配列の添字は0から始まるものとする。 空欄に入る最も適切なものを選べ。
この動画を見る
このプログラムはxy平面上を動く点をプロットするものである。 動く点は、各繰り返しごとにx軸方向に0.1、y軸方向に+1または-1だけ動く。 y軸方向に+1動くか-1動くかはランダムである。 乱数は0以上1未満の実数をランダムに返す関数であり、要素追加(配列, 値)は配列の末尾に新しい要素を追加する関数である。 また、プロットする(配列X, 配列Y)は2つの配列の同じ添字の要素を組みとして、xy平面に座標をプロットして表示する関数である。 配列の添字は0から始まるものとする。 空欄に入る最も適切なものを選べ。
327 モンテカルロ法:円周率を確率的に推定する
単元:
#情報Ⅰ(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師:
めいちゃんねる
問題文全文(内容文):
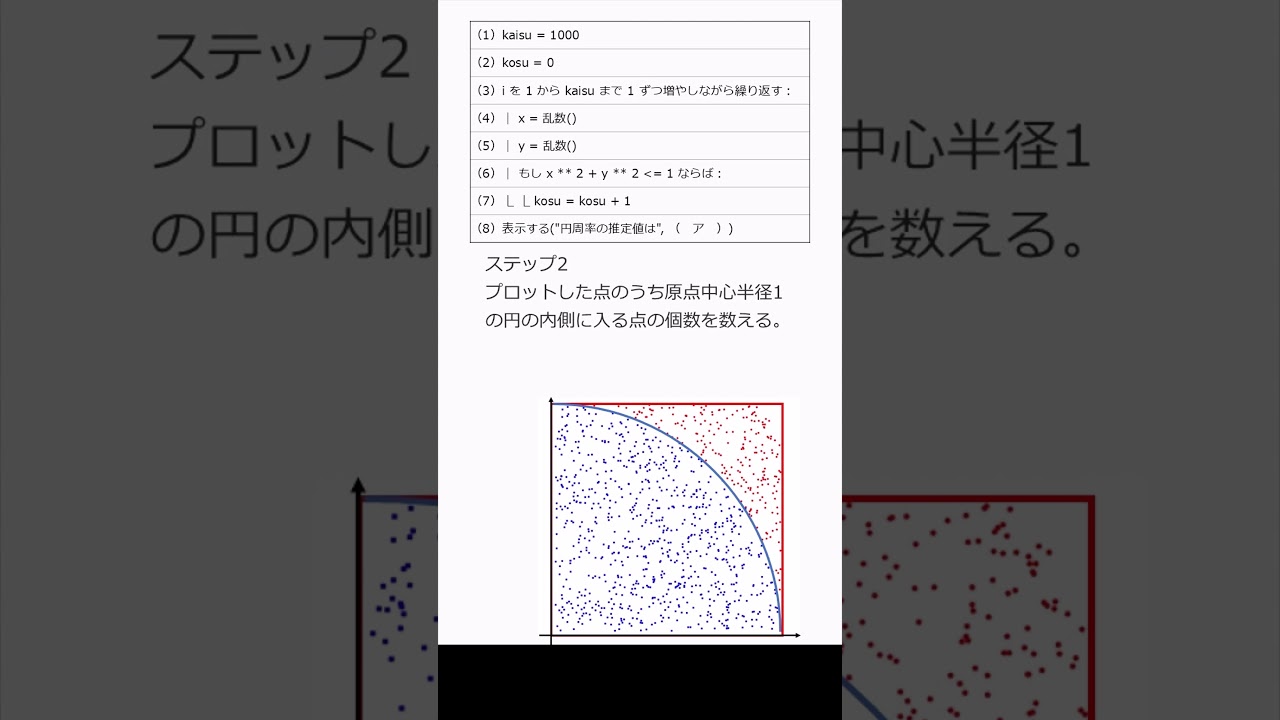
このプログラムはモンテカルロ法を用いて円周率の推定値を求めるものである。 乱数は0以上1未満の実数をランダムに返す関数である。 空欄に入る最も適切なものを選べ。
この動画を見る
このプログラムはモンテカルロ法を用いて円周率の推定値を求めるものである。 乱数は0以上1未満の実数をランダムに返す関数である。 空欄に入る最も適切なものを選べ。
326 検査の精度をシミュレーション:偽陽性は意外と多い!? #shorts
単元:
#情報Ⅰ(高校生)#プログラミング#基本的なプログラミング#配列と関数
指導講師:
めいちゃんねる
問題文全文(内容文):
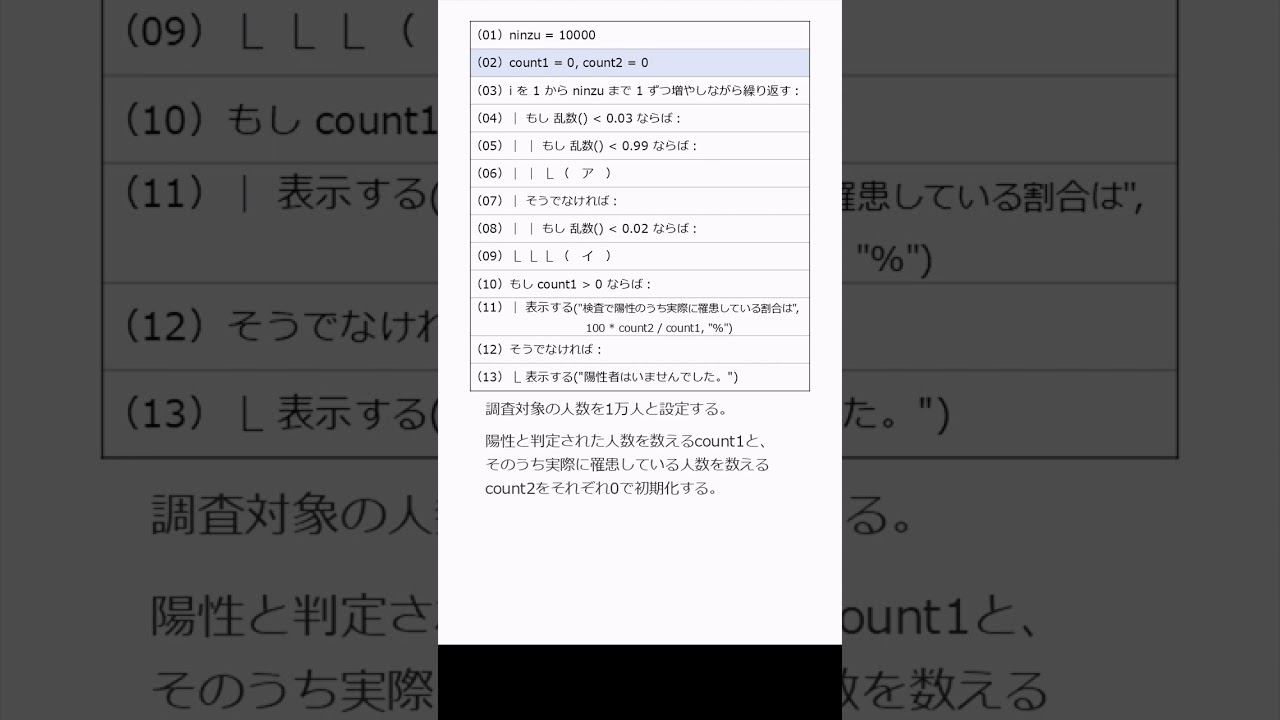
ある感染症に人口の3%が罹患しているという。
現在使われている検査薬は、罹患している人に使用すると99%の割合で正しく陽性と判定し、罹患していない人に使用すると98%の割合で正しく陰性と判定する。
このプログラムは、この検査薬を1万人に使って陽性と判定された人のうち実際に罹患している人の割合を算出するものである。
乱数は0以上1未満の実数をランダムに返す関数である。
空欄に入る最も適切なものを選べ。
(01)ninzu=10000
(02)count1=0,count2=0
(03)iを1からninzuまで1ずつ増やしながら繰り返す:
(04)|もし乱数()<0.03ならば:
(05)||もし乱数()<0.99ならば:
(06)||L(ア)
(07)|そうでなければ:
(08)||もし乱数()0ならば:
(11)|表示する("検査で陽性のうち実際に罹患している割合は",100*count2/count1,"%")
(12)そうでなければ:
(13)L表示する("陽性者はいませんでした。")
この動画を見る
ある感染症に人口の3%が罹患しているという。
現在使われている検査薬は、罹患している人に使用すると99%の割合で正しく陽性と判定し、罹患していない人に使用すると98%の割合で正しく陰性と判定する。
このプログラムは、この検査薬を1万人に使って陽性と判定された人のうち実際に罹患している人の割合を算出するものである。
乱数は0以上1未満の実数をランダムに返す関数である。
空欄に入る最も適切なものを選べ。
(01)ninzu=10000
(02)count1=0,count2=0
(03)iを1からninzuまで1ずつ増やしながら繰り返す:
(04)|もし乱数()<0.03ならば:
(05)||もし乱数()<0.99ならば:
(06)||L(ア)
(07)|そうでなければ:
(08)||もし乱数()0ならば:
(11)|表示する("検査で陽性のうち実際に罹患している割合は",100*count2/count1,"%")
(12)そうでなければ:
(13)L表示する("陽性者はいませんでした。")
【数Ⅱ】【式と証明】整式の割り算2 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#模試解説・過去問解説
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の第1式が第2式で割り切れるように、定数$l,m$の値を定めよ。
(1)$ x^3+lx^2+mx+2 ,x^2+2x+2
(2) $x^3+lx^2+m ,(x+2)^2$
この動画を見る
次の第1式が第2式で割り切れるように、定数$l,m$の値を定めよ。
(1)$ x^3+lx^2+mx+2 ,x^2+2x+2
(2) $x^3+lx^2+m ,(x+2)^2$
325 同じ誕生日の組が現れる確率:意外と少ない人数で現れる有名問題 #shorts
単元:
#情報Ⅰ(高校生)#プログラミング#基本的なプログラミング#配列と関数
指導講師:
めいちゃんねる
問題文全文(内容文):
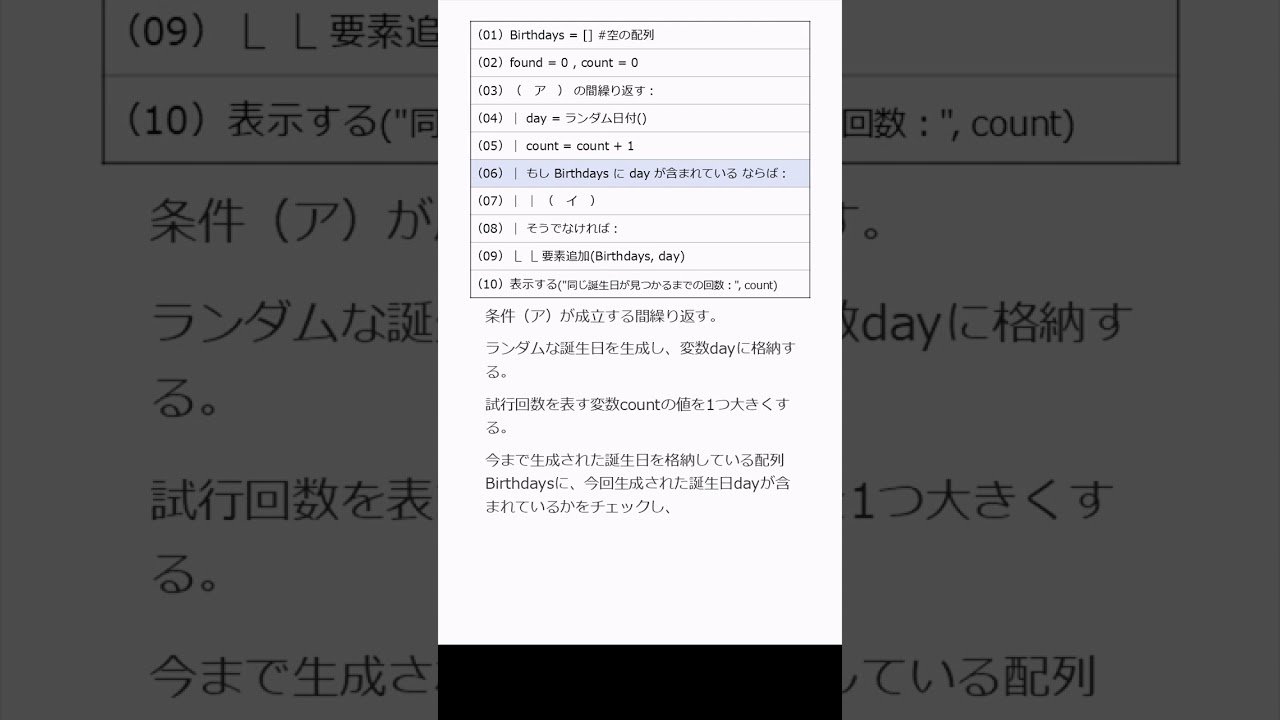
ランダムに誕生日を生成していき、初めて同じ誕生日が現れるまでの回数をカウントするプログラムとなるように、空欄に入る最も適切なものを選べ。
(01)Birthdays=[]#空の配列
(02)found=0,count=0
(03)(ア)の間繰り返す:
(04)|day=ランダム日付()
(05)|count=count+1
(06)|もしBirthdaysにdayが含まれているならば:
(07)||(イ)
(08)|そうでなければ:
(09)LL要素追加(Birthdays,day)
(10)表示する("同じ誕生日が見つかるまでの回数:",count)
1,found=0
2,found=1
3,found==0
4,found==1
この動画を見る
ランダムに誕生日を生成していき、初めて同じ誕生日が現れるまでの回数をカウントするプログラムとなるように、空欄に入る最も適切なものを選べ。
(01)Birthdays=[]#空の配列
(02)found=0,count=0
(03)(ア)の間繰り返す:
(04)|day=ランダム日付()
(05)|count=count+1
(06)|もしBirthdaysにdayが含まれているならば:
(07)||(イ)
(08)|そうでなければ:
(09)LL要素追加(Birthdays,day)
(10)表示する("同じ誕生日が見つかるまでの回数:",count)
1,found=0
2,found=1
3,found==0
4,found==1
共テ本番レベル模試直前!共テ問題集「情報Ⅰ」第3回全問解説!

単元:
#情報Ⅰ(高校生)#情報社会#情報デザイン#デジタル#ネットワーク#情報社会と問題解決#情報セキュリティと法規#情報デザインの基礎#情報デザインの活用#デジタル化された情報とその表し方#さまざまな情報システム#情報システムを支えるデータベース
指導講師:
理数個別チャンネル
問題文全文(内容文):
共テ本番レベル模試直前!共テ問題集「情報Ⅰ」第3回全問解説になります!
この動画を見る
共テ本番レベル模試直前!共テ問題集「情報Ⅰ」第3回全問解説になります!
共テ本番レベル模試直前!共テ問題集「情報Ⅰ」第2回全問解説!

単元:
#情報Ⅰ(高校生)#情報社会#情報デザイン#デジタル#ネットワーク#情報社会と問題解決#情報セキュリティと法規#情報デザインの基礎#情報デザインの活用#デジタル化された情報とその表し方#さまざまな情報システム#情報システムを支えるデータベース
指導講師:
理数個別チャンネル
問題文全文(内容文):
共テ本番レベル模試直前!共テ問題集「情報Ⅰ」第2回全問解説になります!
この動画を見る
共テ本番レベル模試直前!共テ問題集「情報Ⅰ」第2回全問解説になります!
共テ本番レベル模試直前!2024年10月共通テスト模試「情報Ⅰ」全問解説!

単元:
#情報Ⅰ(高校生)#情報社会#情報デザイン#デジタル#ネットワーク#情報社会と問題解決#情報セキュリティと法規#情報デザインの基礎#情報デザインの活用#デジタル化された情報とその表し方#さまざまな情報システム#情報システムを支えるデータベース
指導講師:
理数個別チャンネル
問題文全文(内容文):
共テ本番レベル模試直前!2024年10月共通テスト模試「情報Ⅰ」全問解説になります!
この動画を見る
共テ本番レベル模試直前!2024年10月共通テスト模試「情報Ⅰ」全問解説になります!
324 コイン投げの結果を度数分布表にまとめる:ばらつきを可視化しよう! #shorts
単元:
#情報Ⅰ(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師:
めいちゃんねる
問題文全文(内容文):
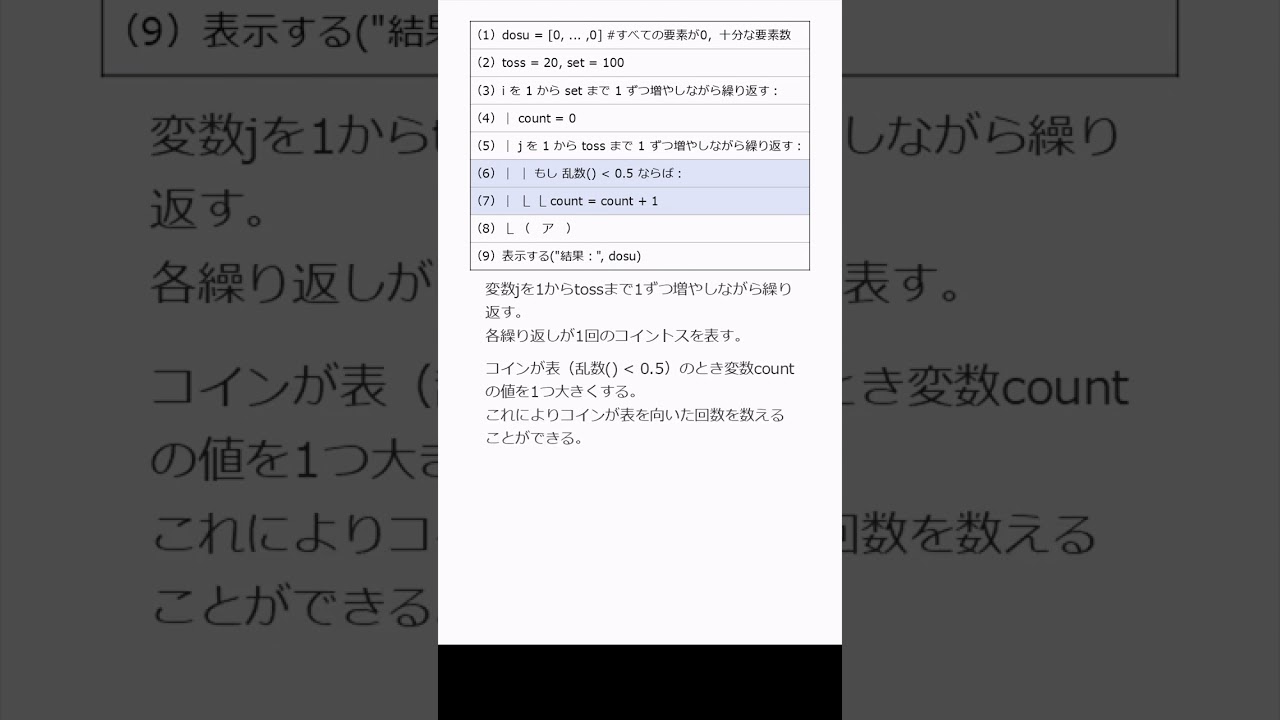
このプログラムはコインを20回投げるという試行を100セット行い、各セットでおもてが出た回数を度数分布表にまとめるものである。
乱数は0以上1未満の実数をランダムに返す関数であり、配列の添字は0から始まるものとする。
空欄に入る最も適切なものを選べ。
(1)dosu=[0,...,0]#すべての要素が0,要素数
(2)toss=20,set=100
(3)iを1からsetまで1ずつ増やしながら繰り返す:
(4)|count=1
(5)|jを1からtossまで1ずつ増やしながら繰り返す:
(6)||もし乱数()<0.5ならば:
(7)|LLcount=count+1
(8)L(ア)
(9)表示する("結果:"doss)
この動画を見る
このプログラムはコインを20回投げるという試行を100セット行い、各セットでおもてが出た回数を度数分布表にまとめるものである。
乱数は0以上1未満の実数をランダムに返す関数であり、配列の添字は0から始まるものとする。
空欄に入る最も適切なものを選べ。
(1)dosu=[0,...,0]#すべての要素が0,要素数
(2)toss=20,set=100
(3)iを1からsetまで1ずつ増やしながら繰り返す:
(4)|count=1
(5)|jを1からtossまで1ずつ増やしながら繰り返す:
(6)||もし乱数()<0.5ならば:
(7)|LLcount=count+1
(8)L(ア)
(9)表示する("結果:"doss)

