 センター試験
センター試験
 センター試験
センター試験
【旧センター試験化学】2020追試第4問 問2アルコールの酸化に関する量的関係の問題

【数Ⅰ】集合と命題:センター試験2013年

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形に関する条件p,q,rを次のように定める。p:3つの内角がすべて異なる q:直角三角形でない r:45度の内角は1つもない。条件pの否定をpバーで表し、同様にq,rはそれぞれ条件qバー、rバーの否定を表すものとする。
[1]命題「r ⇒ (pまたはq)」の対偶は「(ア)⇒r」である。(ア)に当てはまるものを, 次の(0)~(3)のうちから1つ選べ。
(0)(pかつq) (1) (pかつq) (2) (pまたはq ) (3) (pまたはq)
[2] 次の(0)~(4)のうち、命題「(pまたはq) ⇒ r」に対する反例となっている三角形は(イ)と(ウ)である。(イ)と(ウ)に当てはまるものを、(0)~(4)のうちから1つずつ選べ。ただし、(イ)と(ウ)の解答の順序は問わない。
(0) 直角二等辺三角形 (1) 内角が30度,45度,105度の三角形 (2) 正三角形 (3) 3辺の長さが3,4,5の三角形 (4) 頂角が45度の二等辺三角形
[3] rは(pまたはq)であるための(エ) 。(エ)に当てはまるものを、次の(0)~(3)のうちから1つ選べ。
(0) 必要十分条件である (1) 必要条件であるが十分条件ではない (2) 十分条件であるが必要条件ではない (3) 必要条件でも十分条件でもない
この動画を見る
三角形に関する条件p,q,rを次のように定める。p:3つの内角がすべて異なる q:直角三角形でない r:45度の内角は1つもない。条件pの否定をpバーで表し、同様にq,rはそれぞれ条件qバー、rバーの否定を表すものとする。
[1]命題「r ⇒ (pまたはq)」の対偶は「(ア)⇒r」である。(ア)に当てはまるものを, 次の(0)~(3)のうちから1つ選べ。
(0)(pかつq) (1) (pかつq) (2) (pまたはq ) (3) (pまたはq)
[2] 次の(0)~(4)のうち、命題「(pまたはq) ⇒ r」に対する反例となっている三角形は(イ)と(ウ)である。(イ)と(ウ)に当てはまるものを、(0)~(4)のうちから1つずつ選べ。ただし、(イ)と(ウ)の解答の順序は問わない。
(0) 直角二等辺三角形 (1) 内角が30度,45度,105度の三角形 (2) 正三角形 (3) 3辺の長さが3,4,5の三角形 (4) 頂角が45度の二等辺三角形
[3] rは(pまたはq)であるための(エ) 。(エ)に当てはまるものを、次の(0)~(3)のうちから1つ選べ。
(0) 必要十分条件である (1) 必要条件であるが十分条件ではない (2) 十分条件であるが必要条件ではない (3) 必要条件でも十分条件でもない
数学「大学入試良問集」【4−1 組分け問題①】を宇宙一わかりやすく

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
何人かの人をいくつかの部屋に分ける問題を考える。
ただし、各部屋は十分に大きく、定員については考慮しなくてよい。
(1)
7人を2つの部屋$A,B$に分ける。
(ⅰ)部屋$A$に3人、部屋$B$に4人となる分け方は全部で何通りあるか。
(ⅱ)どの部屋も1人以上になる分け方は全部で何通りあるか。
(ⅲ)(ⅱ)のうち、部屋$A$の人数が奇数である分け方は全部で何通りあるか。
(2)
4人を三つの部屋$A,B,C$に分ける。
どの部屋も1人以上になる分け方は全部で何通りあるか。
(3)
大人4人、こども3人の計7人を三つの部屋$A,B,C$に分ける。
(ⅰ)どの部屋も大人が1人以上になる分け方は全部で何通りあるか。
(ⅱ)(ⅱ)のうち、三つの部屋に子ども3人が1人ずつ入る分け方は全部で何通りあるか。
(ⅲ)どの部屋も大人が1人以上で、かつ、各部屋とも2人以上になる分け方は全部で何通りあるか。
この動画を見る
何人かの人をいくつかの部屋に分ける問題を考える。
ただし、各部屋は十分に大きく、定員については考慮しなくてよい。
(1)
7人を2つの部屋$A,B$に分ける。
(ⅰ)部屋$A$に3人、部屋$B$に4人となる分け方は全部で何通りあるか。
(ⅱ)どの部屋も1人以上になる分け方は全部で何通りあるか。
(ⅲ)(ⅱ)のうち、部屋$A$の人数が奇数である分け方は全部で何通りあるか。
(2)
4人を三つの部屋$A,B,C$に分ける。
どの部屋も1人以上になる分け方は全部で何通りあるか。
(3)
大人4人、こども3人の計7人を三つの部屋$A,B,C$に分ける。
(ⅰ)どの部屋も大人が1人以上になる分け方は全部で何通りあるか。
(ⅱ)(ⅱ)のうち、三つの部屋に子ども3人が1人ずつ入る分け方は全部で何通りあるか。
(ⅲ)どの部屋も大人が1人以上で、かつ、各部屋とも2人以上になる分け方は全部で何通りあるか。
共通テスト2021年数学詳しい解説〜共通テスト2021年2B第1問〜三角関数、指数関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#指数関数と対数関数#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#センター試験・共通テスト関連#共通テスト#センター試験#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第1問}$
[1](1)次の問題$A$について考えよう。
$\boxed{\boxed{問題A} 関数y=\sin\theta+\sqrt3\cos\theta\left(0 \leqq \theta \leqq \displaystyle \frac{\pi}{2}\right)$の最大値を求めよ。}$
$\sin\displaystyle \frac{\pi}{\boxed{\ \ ア\ \ }}=\displaystyle \frac{\sqrt3}{2},$ $\cos\displaystyle \frac{\pi}{\boxed{\ \ ア\ \ }}=\displaystyle \frac{1}{2}$
であるから、三角関数の合成により
$y=\boxed{\ \ イ\ \ }\sin\left(\theta+\displaystyle \frac{\pi}{\boxed{\ \ ア\ \ }}\right)$
と変形できる。よって、$y$は$\theta=\displaystyle \frac{\pi}{\boxed{\ \ ウ\ \ }}$で最大値$\ \boxed{\ \ エ\ \ }\ $をとる。
(2)$p$を定数とし、次の問題$B$について考えよう。
$\boxed{\boxed{問題B} 関数y=\sin\theta+p\cos\theta\left(0 \leqq \theta \leqq \frac{\pi}{2}\right)の最大値を求めよ。}$
$(\textrm{i})$ $p=0$のとき、$y$は$\theta=\displaystyle \frac{\pi}{\boxed{\ \ オ\ \ }}$で最大値$\ \boxed{\ \ カ\ \ }\ $をとる。
$(\textrm{ii})$ $p \gt 0$のときは、加法定理
$\cos(\theta-\alpha)=\cos\theta\cos\alpha$$+\sin\theta\sin\alpha$
を用いると
$y=\sin\theta+p\cos\theta$$=\sqrt{\boxed{\boxed{\ \ キ\ \ }}}\cos(\theta-\alpha)$
と表すことができる。ただし、$\alpha$は
$\sin\alpha=\displaystyle \frac{\boxed{\boxed{\ \ ク\ \ }}}{\sqrt{\boxed{\boxed{\ \ キ\ \ }}}}$、$\cos\alpha=\frac{\boxed{\boxed{\ \ ケ\ \ }}}{\sqrt{\boxed{\boxed{\ \ キ\ \ }}}}$、$0 \lt \alpha \lt \displaystyle \frac{\pi}{2}$
を満たすものとする。このとき、$y$は$\theta=\boxed{\boxed{\ \ コ\ \ }}$で最大値
$\sqrt{\boxed{\boxed{\ \ サ\ \ }}}$をとる。
$(\textrm{iii})$ $p \lt 0$のとき、$y$は$\theta=\boxed{\boxed{\ \ シ\ \ }}$で最大値$\boxed{\boxed{\ \ ス\ \ }}$をとる。
$\boxed{\boxed{\ \ キ\ \ }}~\boxed{\boxed{\ \ ケ\ \ }}、\boxed{\boxed{\ \ サ\ \ }}、\boxed{\boxed{\ \ ス\ \ }}$の解答群(同じものを繰り返
し選んでもよい。)
⓪$-1$
①$1$
②$-p$
③$p$
④$1-p$
⑤$1+p$
⑥$-p^2$
⑦$p^2$
⑧$1-p^2$
⑨$1+p^2$
ⓐ$(1-p)^2$
ⓑ$(1+p)^2$
$\boxed{\boxed{\ \ コ\ \ }}、\boxed{\boxed{\ \ シ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$0$
①$\alpha$
②$\displaystyle \frac{\pi}{2}$
[2]二つの関数$f(x)=\displaystyle \frac{2^x+2^{-x}}{2}$、$g(x)=\displaystyle \frac{2^x-2^{-x}}{2}$ について考える。
(1)$f(0)=\boxed{\ \ セ\ \ }、g(0)=\boxed{\ \ ソ\ \ }$である。また、$f(x)$は相加平均
と相乗平均の関係から、$x=\boxed{\ \ タ\ \ }$で最小値$\ \boxed{\ \ チ\ \ }$ をとる。
$g(x)=-2$ となる$x$の値は$\log_2\left(\sqrt{\boxed{\ \ ツ\ \ }}-\boxed{\ \ テ\ \ }\right)$である。
(3)次の①~④は、$x$にどのような値を代入しても常に成り立つ。
$f(-x)=\boxed{\boxed{\ \ ト\ \ }}$ $\cdots$①
$g(-x)=\boxed{\boxed{\ \ ナ\ \ }}$ $\cdots$②
$\left\{f(x)\right\}^2-\left\{g(x)\right\}^2=\boxed{\ \ ニ\ \ }$ $\cdots$③
$g(2x)=\boxed{\ \ ヌ\ \ }\ f(x)g(x)$ $\cdots$④
$\boxed{\boxed{\ \ ト\ \ }}、\boxed{\boxed{\ \ ナ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$f(x)$
①$-f(x)$
②$g(x)$
③$-g(x)$
(3)花子さんと太郎さんは、$f(x)$と$g(x)$の性質について話している。
花子:①~④は三角関数の性質に似ているね。
太郎:三角関数の加法定理に類似した式($\textrm{A}$)~($\textrm{D}$)を考えてみたけど、
常に成り立つ式はあるだろうか。
花子:成り立たない式を見つけるために、式($\textrm{A}$)~($\textrm{D}$)の$\beta$に何か具体
的な値を代入して調べてみたらどうかな。
太郎さんが考えた式
$f(\alpha-\beta)=f(\alpha)g(\beta)+g(\alpha)f(\beta)$ $\cdots(\textrm{A})$
$f(\alpha+\beta)=f(\alpha)f(\beta)+g(\alpha)g(\beta)$ $\cdots(\textrm{B})$
$g(\alpha-\beta)=f(\alpha)f(\beta)+g(\alpha)g(\beta)$ $\cdots(\textrm{C})$
$g(\alpha+\beta)=f(\alpha)g(\beta)-g(\alpha)f(\beta)$ $\cdots(\textrm{D})$
(1),(2)で示されたことのいくつかを利用すると、式($\textrm{A}$)~($\textrm{D}$)のうち、
$\boxed{\boxed{\ \ ネ\ \ }}$以外の三つは成り立たないことが分かる。$\boxed{\boxed{\ \ ネ\ \ }}$は左辺と右辺
をそれぞれ計算することによって成り立つことが確かめられる。
$\boxed{\boxed{\ \ ネ\ \ }}$の解答群
⓪$(\textrm{A})$
①$(\textrm{B})$
②$(\textrm{C})$
③$(\textrm{D})$
2021共通テスト過去問
この動画を見る
${\large第1問}$
[1](1)次の問題$A$について考えよう。
$\boxed{\boxed{問題A} 関数y=\sin\theta+\sqrt3\cos\theta\left(0 \leqq \theta \leqq \displaystyle \frac{\pi}{2}\right)$の最大値を求めよ。}$
$\sin\displaystyle \frac{\pi}{\boxed{\ \ ア\ \ }}=\displaystyle \frac{\sqrt3}{2},$ $\cos\displaystyle \frac{\pi}{\boxed{\ \ ア\ \ }}=\displaystyle \frac{1}{2}$
であるから、三角関数の合成により
$y=\boxed{\ \ イ\ \ }\sin\left(\theta+\displaystyle \frac{\pi}{\boxed{\ \ ア\ \ }}\right)$
と変形できる。よって、$y$は$\theta=\displaystyle \frac{\pi}{\boxed{\ \ ウ\ \ }}$で最大値$\ \boxed{\ \ エ\ \ }\ $をとる。
(2)$p$を定数とし、次の問題$B$について考えよう。
$\boxed{\boxed{問題B} 関数y=\sin\theta+p\cos\theta\left(0 \leqq \theta \leqq \frac{\pi}{2}\right)の最大値を求めよ。}$
$(\textrm{i})$ $p=0$のとき、$y$は$\theta=\displaystyle \frac{\pi}{\boxed{\ \ オ\ \ }}$で最大値$\ \boxed{\ \ カ\ \ }\ $をとる。
$(\textrm{ii})$ $p \gt 0$のときは、加法定理
$\cos(\theta-\alpha)=\cos\theta\cos\alpha$$+\sin\theta\sin\alpha$
を用いると
$y=\sin\theta+p\cos\theta$$=\sqrt{\boxed{\boxed{\ \ キ\ \ }}}\cos(\theta-\alpha)$
と表すことができる。ただし、$\alpha$は
$\sin\alpha=\displaystyle \frac{\boxed{\boxed{\ \ ク\ \ }}}{\sqrt{\boxed{\boxed{\ \ キ\ \ }}}}$、$\cos\alpha=\frac{\boxed{\boxed{\ \ ケ\ \ }}}{\sqrt{\boxed{\boxed{\ \ キ\ \ }}}}$、$0 \lt \alpha \lt \displaystyle \frac{\pi}{2}$
を満たすものとする。このとき、$y$は$\theta=\boxed{\boxed{\ \ コ\ \ }}$で最大値
$\sqrt{\boxed{\boxed{\ \ サ\ \ }}}$をとる。
$(\textrm{iii})$ $p \lt 0$のとき、$y$は$\theta=\boxed{\boxed{\ \ シ\ \ }}$で最大値$\boxed{\boxed{\ \ ス\ \ }}$をとる。
$\boxed{\boxed{\ \ キ\ \ }}~\boxed{\boxed{\ \ ケ\ \ }}、\boxed{\boxed{\ \ サ\ \ }}、\boxed{\boxed{\ \ ス\ \ }}$の解答群(同じものを繰り返
し選んでもよい。)
⓪$-1$
①$1$
②$-p$
③$p$
④$1-p$
⑤$1+p$
⑥$-p^2$
⑦$p^2$
⑧$1-p^2$
⑨$1+p^2$
ⓐ$(1-p)^2$
ⓑ$(1+p)^2$
$\boxed{\boxed{\ \ コ\ \ }}、\boxed{\boxed{\ \ シ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$0$
①$\alpha$
②$\displaystyle \frac{\pi}{2}$
[2]二つの関数$f(x)=\displaystyle \frac{2^x+2^{-x}}{2}$、$g(x)=\displaystyle \frac{2^x-2^{-x}}{2}$ について考える。
(1)$f(0)=\boxed{\ \ セ\ \ }、g(0)=\boxed{\ \ ソ\ \ }$である。また、$f(x)$は相加平均
と相乗平均の関係から、$x=\boxed{\ \ タ\ \ }$で最小値$\ \boxed{\ \ チ\ \ }$ をとる。
$g(x)=-2$ となる$x$の値は$\log_2\left(\sqrt{\boxed{\ \ ツ\ \ }}-\boxed{\ \ テ\ \ }\right)$である。
(3)次の①~④は、$x$にどのような値を代入しても常に成り立つ。
$f(-x)=\boxed{\boxed{\ \ ト\ \ }}$ $\cdots$①
$g(-x)=\boxed{\boxed{\ \ ナ\ \ }}$ $\cdots$②
$\left\{f(x)\right\}^2-\left\{g(x)\right\}^2=\boxed{\ \ ニ\ \ }$ $\cdots$③
$g(2x)=\boxed{\ \ ヌ\ \ }\ f(x)g(x)$ $\cdots$④
$\boxed{\boxed{\ \ ト\ \ }}、\boxed{\boxed{\ \ ナ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$f(x)$
①$-f(x)$
②$g(x)$
③$-g(x)$
(3)花子さんと太郎さんは、$f(x)$と$g(x)$の性質について話している。
花子:①~④は三角関数の性質に似ているね。
太郎:三角関数の加法定理に類似した式($\textrm{A}$)~($\textrm{D}$)を考えてみたけど、
常に成り立つ式はあるだろうか。
花子:成り立たない式を見つけるために、式($\textrm{A}$)~($\textrm{D}$)の$\beta$に何か具体
的な値を代入して調べてみたらどうかな。
太郎さんが考えた式
$f(\alpha-\beta)=f(\alpha)g(\beta)+g(\alpha)f(\beta)$ $\cdots(\textrm{A})$
$f(\alpha+\beta)=f(\alpha)f(\beta)+g(\alpha)g(\beta)$ $\cdots(\textrm{B})$
$g(\alpha-\beta)=f(\alpha)f(\beta)+g(\alpha)g(\beta)$ $\cdots(\textrm{C})$
$g(\alpha+\beta)=f(\alpha)g(\beta)-g(\alpha)f(\beta)$ $\cdots(\textrm{D})$
(1),(2)で示されたことのいくつかを利用すると、式($\textrm{A}$)~($\textrm{D}$)のうち、
$\boxed{\boxed{\ \ ネ\ \ }}$以外の三つは成り立たないことが分かる。$\boxed{\boxed{\ \ ネ\ \ }}$は左辺と右辺
をそれぞれ計算することによって成り立つことが確かめられる。
$\boxed{\boxed{\ \ ネ\ \ }}$の解答群
⓪$(\textrm{A})$
①$(\textrm{B})$
②$(\textrm{C})$
③$(\textrm{D})$
2021共通テスト過去問
2020年センター試験解説。福田の入試問題解説〜2020年センター試験IIB第5問〜確率分布と統計的な推測
単元:
#大学入試過去問(数学)#確率分布と統計的な推測#確率分布#統計的な推測#センター試験・共通テスト関連#センター試験#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large第5問}$
ある市の市立図書館の利用状況について調査を行った。
(1)ある高校の生徒720人全員を対象に、ある1週間に市立図書館で借りた本の
冊数について調査を行った。
その結果、1冊も借りなかった生徒が612人、1冊借りた生徒が54人、
2冊借りた生徒が36人であり、3冊借りた生徒が18人であった。
4冊以上借りた生徒はいなかった。
この高校の生徒から1人を無作為に選んだ時、その生徒が借りた本の冊数
を表す確率変数を$X$とする。
このとき、$X$の平均(期待値)は$E(X)=\displaystyle \frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$であり、$X^2$の平均は
$E(X^2)=\displaystyle \frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$である。よって、$X$の標準偏差は
$\sigma(X)=\displaystyle \frac{\sqrt{\boxed{\ \ オ\ \ }}}{\boxed{\ \ カ\ \ }}\displaystyle$ である。
(2)市内の高校生全員を母集団とし、ある1週間に市立図書館を利用した生徒の
割合(母比率)を$p$とする。この母集団から600人を無作為に選んだ時、その
1週間に市立図書館を利用した生徒の数を確率変数$Y$で表す。
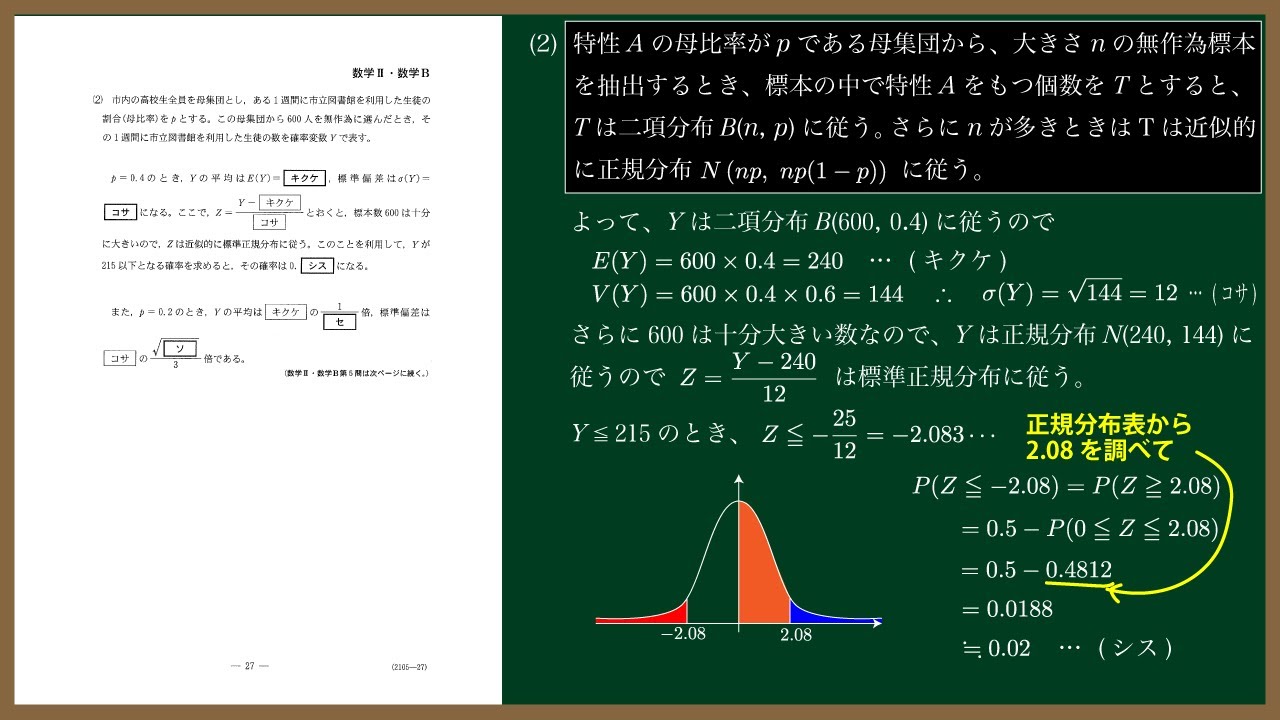
$p=0.4$のとき、$Y$の平均は$E(Y)=\boxed{\ \ キクケ\ \ }$、標準偏差は$\sigma(Y)=\boxed{\ \ コサ\ \ }$
になる。ここで、$Z=\displaystyle \frac{Y-\boxed{\ \ キクケ\ \ }}{\boxed{\ \ コサ\ \ }}\displaystyle$ とおくと、標本数600は
十分に大きいので、$Z$は近似的に標準正規分布に従う。このことを利用して、
$Y$が215以下となる確率を求めると、その確率は$0.\boxed{\ \ シス\ \ }$になる。
また、$p=0.2$のとき、$Y$の平均は$\boxed{\ \ キクケ\ \ }$の$\displaystyle \frac{1}{\boxed{\ \ セ\ \ }}$倍、
標準偏差は$\boxed{\ \ コサ\ \ }$の$\displaystyle \frac{\sqrt{\boxed{\ \ ソ\ \ }}}{3}$倍である。
(3)市立図書館に利用者登録のある高校生全員を母集団とする。1回あたりの
利用時間(分)を表す確率変数を$W$とし、$W$は母平均$m$,母標準偏差30の分布
に従うとする。この母集団から大きさ$n$の標本$W_1,W_2,\ldots,W_n$を無作為に
抽出した。
利用時間が60分をどの程度超えるかについて調査するために
$U_1=W_1-60, U_2=W_2-60, \ldots, U_n=W_n-60$
とおくと、確率変数$U_1,U_2, \cdots, U_n$の平均と標準偏差はそれぞれ
$E(U_1)=E(U_2)=\cdots=E(U_n)$$=m-\boxed{\ \ タチ\ \ }$
$\sigma(U_1)=\sigma(U_2)=\cdots=\sigma(U_n)$$=\boxed{\ \ ツテ\ \ }$
である。
ここで、$t=m-60$として、$t$に対する信頼度95%の信頼区間を求めよう。
この母集団から無作為抽出された100人の生徒に対して$U_1,U_2, \cdots,U_m$の
値を調べたところ、その標本平均の値が50分であった。標本数は十分大きい
ことを利用して、この信頼区間を求めると
$\boxed{\ \ トナ\ \ }.\boxed{\ \ ニ\ \ } \leqq t \leqq \boxed{\ \ ヌネ\ \ }.\boxed{\ \ ノ\ \ }$
になる。
2020センター試験過去問
この動画を見る
${\large第5問}$
ある市の市立図書館の利用状況について調査を行った。
(1)ある高校の生徒720人全員を対象に、ある1週間に市立図書館で借りた本の
冊数について調査を行った。
その結果、1冊も借りなかった生徒が612人、1冊借りた生徒が54人、
2冊借りた生徒が36人であり、3冊借りた生徒が18人であった。
4冊以上借りた生徒はいなかった。
この高校の生徒から1人を無作為に選んだ時、その生徒が借りた本の冊数
を表す確率変数を$X$とする。
このとき、$X$の平均(期待値)は$E(X)=\displaystyle \frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$であり、$X^2$の平均は
$E(X^2)=\displaystyle \frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$である。よって、$X$の標準偏差は
$\sigma(X)=\displaystyle \frac{\sqrt{\boxed{\ \ オ\ \ }}}{\boxed{\ \ カ\ \ }}\displaystyle$ である。
(2)市内の高校生全員を母集団とし、ある1週間に市立図書館を利用した生徒の
割合(母比率)を$p$とする。この母集団から600人を無作為に選んだ時、その
1週間に市立図書館を利用した生徒の数を確率変数$Y$で表す。
$p=0.4$のとき、$Y$の平均は$E(Y)=\boxed{\ \ キクケ\ \ }$、標準偏差は$\sigma(Y)=\boxed{\ \ コサ\ \ }$
になる。ここで、$Z=\displaystyle \frac{Y-\boxed{\ \ キクケ\ \ }}{\boxed{\ \ コサ\ \ }}\displaystyle$ とおくと、標本数600は
十分に大きいので、$Z$は近似的に標準正規分布に従う。このことを利用して、
$Y$が215以下となる確率を求めると、その確率は$0.\boxed{\ \ シス\ \ }$になる。
また、$p=0.2$のとき、$Y$の平均は$\boxed{\ \ キクケ\ \ }$の$\displaystyle \frac{1}{\boxed{\ \ セ\ \ }}$倍、
標準偏差は$\boxed{\ \ コサ\ \ }$の$\displaystyle \frac{\sqrt{\boxed{\ \ ソ\ \ }}}{3}$倍である。
(3)市立図書館に利用者登録のある高校生全員を母集団とする。1回あたりの
利用時間(分)を表す確率変数を$W$とし、$W$は母平均$m$,母標準偏差30の分布
に従うとする。この母集団から大きさ$n$の標本$W_1,W_2,\ldots,W_n$を無作為に
抽出した。
利用時間が60分をどの程度超えるかについて調査するために
$U_1=W_1-60, U_2=W_2-60, \ldots, U_n=W_n-60$
とおくと、確率変数$U_1,U_2, \cdots, U_n$の平均と標準偏差はそれぞれ
$E(U_1)=E(U_2)=\cdots=E(U_n)$$=m-\boxed{\ \ タチ\ \ }$
$\sigma(U_1)=\sigma(U_2)=\cdots=\sigma(U_n)$$=\boxed{\ \ ツテ\ \ }$
である。
ここで、$t=m-60$として、$t$に対する信頼度95%の信頼区間を求めよう。
この母集団から無作為抽出された100人の生徒に対して$U_1,U_2, \cdots,U_m$の
値を調べたところ、その標本平均の値が50分であった。標本数は十分大きい
ことを利用して、この信頼区間を求めると
$\boxed{\ \ トナ\ \ }.\boxed{\ \ ニ\ \ } \leqq t \leqq \boxed{\ \ ヌネ\ \ }.\boxed{\ \ ノ\ \ }$
になる。
2020センター試験過去問
最速。2020年センター試験解説。福田の入試問題解説〜2020年センター試験IA第5問〜平面図形、チェバの定理、メネラウスの定理、方べきの定理

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#内心・外心・重心とチェバ・メネラウス#方べきの定理と2つの円の関係#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第5問}$
$\triangle ABC$において、辺$BC$を$7:1$に内分する点を$D$とし、辺$AC$を$7:1$に
内分する点を$E$とする。線分$AD$と線分$BE$の交点を$F$とし、直線$CF$
と辺$AB$の交点を$G$とすると
$\displaystyle \frac{GB}{AG}=\boxed{\ \ ア\ \ }, \displaystyle \frac{FD}{AF}=\displaystyle \frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }},$$ \displaystyle \frac{FC}{GF}=\displaystyle \frac{\boxed{\ \ エ\ \ }}{\boxed{\ \ オ\ \ }}$
である。したがって
$\displaystyle \frac{\triangle CDGの面積}{\triangle BFGの面積}=\displaystyle \frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キク\ \ }}\displaystyle$
となる。
4点$B,D,F,G$が同一円周上にあり、かつ$FD=1$のとき
$AB=\boxed{\ \ ケコ\ \ }$
である。さらに、$AE=3\sqrt7$とするとき、$AE・AC=\boxed{\ \ サシ\ \ }$であり
$\angle AEG=\boxed{\ \ ス\ \ }$
である。$\boxed{\ \ ス\ \ }$に当てはまるものを、次の⓪~③のうちから一つ選べ。
⓪$\angle BGE$
①$\angle ADB$
②$\angle ABC$
③$\angle BAD$
2020センター試験過去問
この動画を見る
${\large第5問}$
$\triangle ABC$において、辺$BC$を$7:1$に内分する点を$D$とし、辺$AC$を$7:1$に
内分する点を$E$とする。線分$AD$と線分$BE$の交点を$F$とし、直線$CF$
と辺$AB$の交点を$G$とすると
$\displaystyle \frac{GB}{AG}=\boxed{\ \ ア\ \ }, \displaystyle \frac{FD}{AF}=\displaystyle \frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }},$$ \displaystyle \frac{FC}{GF}=\displaystyle \frac{\boxed{\ \ エ\ \ }}{\boxed{\ \ オ\ \ }}$
である。したがって
$\displaystyle \frac{\triangle CDGの面積}{\triangle BFGの面積}=\displaystyle \frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キク\ \ }}\displaystyle$
となる。
4点$B,D,F,G$が同一円周上にあり、かつ$FD=1$のとき
$AB=\boxed{\ \ ケコ\ \ }$
である。さらに、$AE=3\sqrt7$とするとき、$AE・AC=\boxed{\ \ サシ\ \ }$であり
$\angle AEG=\boxed{\ \ ス\ \ }$
である。$\boxed{\ \ ス\ \ }$に当てはまるものを、次の⓪~③のうちから一つ選べ。
⓪$\angle BGE$
①$\angle ADB$
②$\angle ABC$
③$\angle BAD$
2020センター試験過去問
2020年センター試験の塾生の結果報告【篠原好】

単元:
#センター試験・共通テスト関連#センター試験#その他#その他
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
「2020年センター試験の塾生の結果」についての報告です。
この動画を見る
「2020年センター試験の塾生の結果」についての報告です。
最速。2020年センター試験解説。福田の入試問題解説〜2020年センター試験IIB第4問〜空間ベクトルと四面体の体積

単元:
#数A#大学入試過去問(数学)#図形の性質#空間ベクトル#空間ベクトル#センター試験・共通テスト関連#センター試験#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\large第4問}$
点$O$を原点とする座標空間に2点
$A(3, 3, -6),$ $B(2+2\sqrt3,$ $2-2\sqrt3, -4)$
をとる。3点$O,A,B$の定める平面を$\alpha$とする。また、$\alpha$に含まれる点$C$は
$\overrightarrow{ OA } \bot \overrightarrow{ OC },$ $\overrightarrow{ OB }・\overrightarrow{ OC }=24$ $\cdots$①
を満たすとする。
(1) $|\overrightarrow{ OA }|=\boxed{\ \ ア\ \ }\sqrt{\boxed{\ \ イ\ \ }},$ $|\overrightarrow{ OB }|=\boxed{\ \ ウ\ \ }\sqrt{\boxed{\ \ エ\ \ }}$であり、
$\overrightarrow{ OA }・\overrightarrow{ OB }=\boxed{\ \ オカ\ \ }$である。
(2)点$C$は平面$\alpha$上にあるので、実数$s,$ $t$を用いて、$\overrightarrow{ OC }=s\ \overrightarrow{ OA }+t\ \overrightarrow{ OB }$と
表すことができる。このとき、①から$s=\displaystyle \frac{\boxed{\ \ キク\ \ }}{\boxed{\ \ ケ\ \ }},$ $t=\boxed{\ \ コ\ \ }$である。
したがって、$|\overrightarrow{ OC }|=\boxed{\ \ サ\ \ }\sqrt{\boxed{\ \ シ\ \ }}$である。
(3)$\overrightarrow{ CB }=\left(\boxed{\ \ ス\ \ }, \boxed{\ \ セ\ \ }, \boxed{\ \ ソタ\ \ }\right)$である。したがって、平面$\alpha$上の
四角形$OABC$は$\boxed{\ \ チ\ \ }$。
$\boxed{\ \ チ\ \ }$に当てはまるものを、次の⓪~④のうちから一つ選べ。
ただし、少なくとも一組の対辺が平行な四角形を台形という。
⓪正方形である
①正方形ではないが、長方形である
②長方形ではないが、平行四辺形である
③平行四辺形ではないが、台形である
④台形ではない
$\overrightarrow{ OA } \bot \overrightarrow{ OC }$であるので、四角形$OABC$の面積は$\boxed{\ \ ツテ\ \ }$である。
(4)$\overrightarrow{ OA } \bot \overrightarrow{ OD },$ $\overrightarrow{ OC }・\overrightarrow{ OD }=2\sqrt6$かつ$z$座標が1であるような点$D$の座標は
$(\boxed{\ \ ト\ \ }+\displaystyle \frac{\sqrt{\boxed{\ \ ナ\ \ }}}{\boxed{\ \ ニ\ \ }},$$ \boxed{\ \ ヌ\ \ }+\displaystyle \frac{\sqrt{\boxed{\ \ ネ\ \ }}}{\boxed{\ \ ノ\ \ }}, 1)$
である。このとき$\angle COD=\boxed{\ \ ハヒ\ \ }°$である。
3点$O,C,D$の定める平面を$\beta$とする。$\alpha$と$\beta$は垂直であるので、三角形
$ABC$を底面とする四面体$DABC$の高さは$\sqrt{\boxed{\ \ フ\ \ }}$である。したがって、
四面体$DABC$の体積は$\boxed{\ \ ヘ\ \ }\sqrt{\boxed{\ \ ホ\ \ }}$ である。
2020センター試験過去問
この動画を見る
${\large第4問}$
点$O$を原点とする座標空間に2点
$A(3, 3, -6),$ $B(2+2\sqrt3,$ $2-2\sqrt3, -4)$
をとる。3点$O,A,B$の定める平面を$\alpha$とする。また、$\alpha$に含まれる点$C$は
$\overrightarrow{ OA } \bot \overrightarrow{ OC },$ $\overrightarrow{ OB }・\overrightarrow{ OC }=24$ $\cdots$①
を満たすとする。
(1) $|\overrightarrow{ OA }|=\boxed{\ \ ア\ \ }\sqrt{\boxed{\ \ イ\ \ }},$ $|\overrightarrow{ OB }|=\boxed{\ \ ウ\ \ }\sqrt{\boxed{\ \ エ\ \ }}$であり、
$\overrightarrow{ OA }・\overrightarrow{ OB }=\boxed{\ \ オカ\ \ }$である。
(2)点$C$は平面$\alpha$上にあるので、実数$s,$ $t$を用いて、$\overrightarrow{ OC }=s\ \overrightarrow{ OA }+t\ \overrightarrow{ OB }$と
表すことができる。このとき、①から$s=\displaystyle \frac{\boxed{\ \ キク\ \ }}{\boxed{\ \ ケ\ \ }},$ $t=\boxed{\ \ コ\ \ }$である。
したがって、$|\overrightarrow{ OC }|=\boxed{\ \ サ\ \ }\sqrt{\boxed{\ \ シ\ \ }}$である。
(3)$\overrightarrow{ CB }=\left(\boxed{\ \ ス\ \ }, \boxed{\ \ セ\ \ }, \boxed{\ \ ソタ\ \ }\right)$である。したがって、平面$\alpha$上の
四角形$OABC$は$\boxed{\ \ チ\ \ }$。
$\boxed{\ \ チ\ \ }$に当てはまるものを、次の⓪~④のうちから一つ選べ。
ただし、少なくとも一組の対辺が平行な四角形を台形という。
⓪正方形である
①正方形ではないが、長方形である
②長方形ではないが、平行四辺形である
③平行四辺形ではないが、台形である
④台形ではない
$\overrightarrow{ OA } \bot \overrightarrow{ OC }$であるので、四角形$OABC$の面積は$\boxed{\ \ ツテ\ \ }$である。
(4)$\overrightarrow{ OA } \bot \overrightarrow{ OD },$ $\overrightarrow{ OC }・\overrightarrow{ OD }=2\sqrt6$かつ$z$座標が1であるような点$D$の座標は
$(\boxed{\ \ ト\ \ }+\displaystyle \frac{\sqrt{\boxed{\ \ ナ\ \ }}}{\boxed{\ \ ニ\ \ }},$$ \boxed{\ \ ヌ\ \ }+\displaystyle \frac{\sqrt{\boxed{\ \ ネ\ \ }}}{\boxed{\ \ ノ\ \ }}, 1)$
である。このとき$\angle COD=\boxed{\ \ ハヒ\ \ }°$である。
3点$O,C,D$の定める平面を$\beta$とする。$\alpha$と$\beta$は垂直であるので、三角形
$ABC$を底面とする四面体$DABC$の高さは$\sqrt{\boxed{\ \ フ\ \ }}$である。したがって、
四面体$DABC$の体積は$\boxed{\ \ ヘ\ \ }\sqrt{\boxed{\ \ ホ\ \ }}$ である。
2020センター試験過去問
最速。2020年センター試験解説。福田の入試問題解説〜2020年センター試験IA第4問〜整数の性質、循環小数と7進法

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第4問}$
(1)$x$を循環小数$2.\dot3\dot6$とする。すなわち
$x=2.363636\cdots$
とする。このとき
$100×x-x=236.\dot3\dot6-2.\dot3\dot6$
であるから、$x$を分数で表すと
$x=\displaystyle \frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウエ\ \ }}$
である。
(2)有理数$y$は、7進法で表すと、二つの数字の並び$ab$が繰り返し現れる循環小数
$2.\dot a\dot b_{(7)}$になるとする。ただし、$a,$ $b$は$0$以上$6$以下の異なる整数である。
このとき
$49×y-y=2ab.\dot a\dot b_{(7)}-2.\dot a\dot b_{(7)}$
であるから
$y=\displaystyle \frac{\boxed{\ \ オカ\ \ }+7×a+b}{\boxed{\ \ キク\ \ }}$
と表せる。
$(\textrm{i})y$が、分子が奇数で分母が$4$である分数で表されるのは
$y=\displaystyle \frac{\boxed{\ \ ケ\ \ }}{4}$ または $y=\displaystyle \frac{\boxed{\ \ コサ\ \ }}{4}$
のときである。$y=\displaystyle \frac{\boxed{\ \ コサ\ \ }}{4}$のときは、$7×a+b=\boxed{\ \ シス\ \ }$であるから
$a=\boxed{\ \ セ\ \ },$ $b=\boxed{\ \ ソ\ \ }$
である。
$(\textrm{ii})y-2$は、分子が$1$で分母が$2$以上の整数である分数で表されるとする。
このような$y$の個数は、全部で$\boxed{\ \ タ\ \ }$個である。
2020センター試験過去問
この動画を見る
${\large第4問}$
(1)$x$を循環小数$2.\dot3\dot6$とする。すなわち
$x=2.363636\cdots$
とする。このとき
$100×x-x=236.\dot3\dot6-2.\dot3\dot6$
であるから、$x$を分数で表すと
$x=\displaystyle \frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウエ\ \ }}$
である。
(2)有理数$y$は、7進法で表すと、二つの数字の並び$ab$が繰り返し現れる循環小数
$2.\dot a\dot b_{(7)}$になるとする。ただし、$a,$ $b$は$0$以上$6$以下の異なる整数である。
このとき
$49×y-y=2ab.\dot a\dot b_{(7)}-2.\dot a\dot b_{(7)}$
であるから
$y=\displaystyle \frac{\boxed{\ \ オカ\ \ }+7×a+b}{\boxed{\ \ キク\ \ }}$
と表せる。
$(\textrm{i})y$が、分子が奇数で分母が$4$である分数で表されるのは
$y=\displaystyle \frac{\boxed{\ \ ケ\ \ }}{4}$ または $y=\displaystyle \frac{\boxed{\ \ コサ\ \ }}{4}$
のときである。$y=\displaystyle \frac{\boxed{\ \ コサ\ \ }}{4}$のときは、$7×a+b=\boxed{\ \ シス\ \ }$であるから
$a=\boxed{\ \ セ\ \ },$ $b=\boxed{\ \ ソ\ \ }$
である。
$(\textrm{ii})y-2$は、分子が$1$で分母が$2$以上の整数である分数で表されるとする。
このような$y$の個数は、全部で$\boxed{\ \ タ\ \ }$個である。
2020センター試験過去問
最速。2020年センター試験解説。福田の入試問題解説〜2020年センター試験IIB第3問〜数列と漸化式、余りの問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#漸化式#センター試験・共通テスト関連#センター試験#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large第3問}$
数列$\left\{a_n\right\}$は、初項$a_1$が$0$であり、$n=1,2,3,\cdots$のとき次の漸化式を
満たすものとする。
$a_{n+1}=$$\displaystyle \frac{n+3}{n+1}\{3a_n+3^{n+1}-$$(n+1)(n+2)\}$ $\cdots$①
(1)$a_2=\boxed{\ \ ア\ \ }$ である。
(2)$b_n=\displaystyle \frac{a_n}{3^n(n+1)(n+2)}$とおき、数列$\left\{b_n\right\}$の一般項を求めよう。
$\left\{b_n\right\}$の初項$b_1$は$\boxed{\ \ イ\ \ }$である。①の両辺を$3^{n+1}(n+2)(n+3)$で
割ると
$b_{n+1}=b_n$$+\displaystyle \frac{\boxed{\ \ ウ\ \ }}{\left(n+\boxed{\ \ エ\ \ }\right)\left(n+\boxed{\ \ オ\ \ }\right)}$$-\left(\displaystyle \frac{1}{\boxed{\ \ カ\ \ }}\right)^{n+1}$
を得る。ただし、$\boxed{\ \ エ\ \ } \lt \boxed{\ \ オ\ \ }$とする。
したがって
$b_{n+1}-b_n=$$\left(\displaystyle \frac{\boxed{\ \ キ\ \ }}{n+\boxed{\ \ エ\ \ }}-\displaystyle \frac{\boxed{\ \ キ\ \ }}{n+\boxed{\ \ オ\ \ }}\right)$$-\left(\displaystyle \frac{1}{\boxed{\ \ カ\ \ }}\right)^{n+1}$
である。
$n$を2以上の自然数とするとき
$\displaystyle \sum_{k=1}^{n-1}\left(\displaystyle \frac{\boxed{\ \ キ\ \ }}{k+\boxed{\ \ エ\ \ }}-\displaystyle \frac{\boxed{\ \ キ\ \ }}{k+\boxed{\ \ オ\ \ }}\right)$$=\displaystyle \frac{1}{\boxed{\ \ ク\ \ }}\left(\displaystyle \frac{n-\boxed{\ \ ケ\ \ }}{n+\boxed{\ \ コ\ \ }}\right)$
$\displaystyle \sum_{k=1}^{n-1}\left(\displaystyle \frac{1}{\boxed{\ \ カ\ \ }}\right)^{k+1}=$$\displaystyle \frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}-\displaystyle \frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\left(\displaystyle \frac{1}{\boxed{\ \ カ\ \ }}\right)^n$
が成り立つことを利用すると
$b_n=\displaystyle \frac{n-\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }\left(n+\boxed{\ \ チ\ \ }\right)}$$+\displaystyle \frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\left(\displaystyle \frac{1}{\boxed{\ \ カ\ \ }}\right)^n$
が得られる。これは$n=1$のときも成り立つ。
(3)(2)により、$\left\{a_n\right\}$の一般項は
$a_n=\boxed{\ \ ツ\ \ }^{n-\boxed{テ}}\left(n^2-\boxed{\ \ ト\ \ }\right)+$$\displaystyle \frac{\left(n+\boxed{\ \ ナ\ \ }\right)\left(n+\boxed{\ \ ニ\ \ }\right)}{\boxed{\ \ ヌ\ \ }}$
で与えられる。ただし、$\boxed{\ \ ナ\ \ } \lt \boxed{\ \ ニ\ \ }$とする。
このことから、すべての自然数$n$について、
$a_n$は整数となることが分かる。
(4)$k$を自然数とする。$a_{3k},a_{3k+1},a_{3k+2}$で割った余りはそれぞれ
$\boxed{\ \ ネ\ \ },$ $\boxed{\ \ ノ\ \ },$ $\boxed{\ \ ハ\ \ }$である。また、$\left\{a_n\right\}$の初項から
第2020項までの和を$3$で割った余りは$\boxed{\ \ ヒ\ \ }$である。
2020センター試験過去問
この動画を見る
${\large第3問}$
数列$\left\{a_n\right\}$は、初項$a_1$が$0$であり、$n=1,2,3,\cdots$のとき次の漸化式を
満たすものとする。
$a_{n+1}=$$\displaystyle \frac{n+3}{n+1}\{3a_n+3^{n+1}-$$(n+1)(n+2)\}$ $\cdots$①
(1)$a_2=\boxed{\ \ ア\ \ }$ である。
(2)$b_n=\displaystyle \frac{a_n}{3^n(n+1)(n+2)}$とおき、数列$\left\{b_n\right\}$の一般項を求めよう。
$\left\{b_n\right\}$の初項$b_1$は$\boxed{\ \ イ\ \ }$である。①の両辺を$3^{n+1}(n+2)(n+3)$で
割ると
$b_{n+1}=b_n$$+\displaystyle \frac{\boxed{\ \ ウ\ \ }}{\left(n+\boxed{\ \ エ\ \ }\right)\left(n+\boxed{\ \ オ\ \ }\right)}$$-\left(\displaystyle \frac{1}{\boxed{\ \ カ\ \ }}\right)^{n+1}$
を得る。ただし、$\boxed{\ \ エ\ \ } \lt \boxed{\ \ オ\ \ }$とする。
したがって
$b_{n+1}-b_n=$$\left(\displaystyle \frac{\boxed{\ \ キ\ \ }}{n+\boxed{\ \ エ\ \ }}-\displaystyle \frac{\boxed{\ \ キ\ \ }}{n+\boxed{\ \ オ\ \ }}\right)$$-\left(\displaystyle \frac{1}{\boxed{\ \ カ\ \ }}\right)^{n+1}$
である。
$n$を2以上の自然数とするとき
$\displaystyle \sum_{k=1}^{n-1}\left(\displaystyle \frac{\boxed{\ \ キ\ \ }}{k+\boxed{\ \ エ\ \ }}-\displaystyle \frac{\boxed{\ \ キ\ \ }}{k+\boxed{\ \ オ\ \ }}\right)$$=\displaystyle \frac{1}{\boxed{\ \ ク\ \ }}\left(\displaystyle \frac{n-\boxed{\ \ ケ\ \ }}{n+\boxed{\ \ コ\ \ }}\right)$
$\displaystyle \sum_{k=1}^{n-1}\left(\displaystyle \frac{1}{\boxed{\ \ カ\ \ }}\right)^{k+1}=$$\displaystyle \frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}-\displaystyle \frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\left(\displaystyle \frac{1}{\boxed{\ \ カ\ \ }}\right)^n$
が成り立つことを利用すると
$b_n=\displaystyle \frac{n-\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }\left(n+\boxed{\ \ チ\ \ }\right)}$$+\displaystyle \frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\left(\displaystyle \frac{1}{\boxed{\ \ カ\ \ }}\right)^n$
が得られる。これは$n=1$のときも成り立つ。
(3)(2)により、$\left\{a_n\right\}$の一般項は
$a_n=\boxed{\ \ ツ\ \ }^{n-\boxed{テ}}\left(n^2-\boxed{\ \ ト\ \ }\right)+$$\displaystyle \frac{\left(n+\boxed{\ \ ナ\ \ }\right)\left(n+\boxed{\ \ ニ\ \ }\right)}{\boxed{\ \ ヌ\ \ }}$
で与えられる。ただし、$\boxed{\ \ ナ\ \ } \lt \boxed{\ \ ニ\ \ }$とする。
このことから、すべての自然数$n$について、
$a_n$は整数となることが分かる。
(4)$k$を自然数とする。$a_{3k},a_{3k+1},a_{3k+2}$で割った余りはそれぞれ
$\boxed{\ \ ネ\ \ },$ $\boxed{\ \ ノ\ \ },$ $\boxed{\ \ ハ\ \ }$である。また、$\left\{a_n\right\}$の初項から
第2020項までの和を$3$で割った余りは$\boxed{\ \ ヒ\ \ }$である。
2020センター試験過去問
最速。2020年センター試験解説。福田の入試問題解説〜2020年センター試験IIB第2問〜微分・積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第2問}$
$a \gt 0$とし、$f(x)=x^2-(4a-2)x+4a^2+1$ とおく。座標平面上で、放物線
$y=x^2+2x+1$ を$C,$放物線$y=f(x)$を$D$とする。また、$l$を$C$と$D$の両方に
接する直線とする。
(1)lの方程式を求めよう。
$l$と$C$は点$(t,$ $t^2+2t+1)$において接するとすると、$l$の方程式は
$y=\left(\boxed{\ \ ア\ \ }\ t+\boxed{\ \ イ\ \ }\right)\ x$$-t^2+\boxed{\ \ ウ\ \ }$ $\cdots$①
である。また、$l$と$D$は点$(s,$ $f(s))$において接するとすると、$l$の方程式は
$y=\left(\boxed{\ \ エ\ \ }\ s-\boxed{\ \ オ\ \ }\ +\boxed{\ \ カ\ \ }\right)\ x$$-s^2+\boxed{\ \ キ\ \ }\ a^2+\boxed{\ \ ク\ \ }$ $\cdots$②
である。ここで、①と②は同じ直線を表しているので、$t=\boxed{\ \ ケ\ \ },$
$s=\boxed{\ \ コ\ \ }\ a$が成り立つ。
したがって、$l$の方程式は$y=\boxed{\ \ サ\ \ }\ x+\boxed{\ \ シ\ \ }$である。
(2)二つの放物線$C,D$の交点のx座標は$\boxed{\ \ ス\ \ }$である。
$C$と直線$\ t,$および直線$x=\boxed{\ \ ス\ \ }$で囲まれた図形の面積を$S$とすると
$S=\displaystyle \frac{a^{\boxed{セ}}}{\boxed{\ \ ソ\ \ }}$である。
(3)$a \geqq \displaystyle \frac{1}{2}$とする。二つの放物線$C,D$と直線$l$で囲まれた図形の中で
$0 \leqq x \leqq 1$を満たす部分の面積$T$は、$a \gt \boxed{\ \ タ\ \ }$のとき、$a$の値によらず
$T=\displaystyle \frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$
であり、$\displaystyle \frac{1}{2} \leqq a \leqq \boxed{\ \ タ\ \ }$のとき
$T=-\boxed{\ \ テ\ \ }\ a^3+\boxed{\ \ ト\ \ }\ a^2$$-\boxed{\ \ ナ\ \ }\ a+\displaystyle \frac{\boxed{\ \ ニ\ \ }}{\boxed{\ \ ヌ\ \ }}$
である。
(4)次に、(2),(3)で定めた$S,T$に対して、$U=2T-3S$とおく。$a$が
$\displaystyle \frac{1}{2} \leqq a \leqq \boxed{\ \ タ\ \ }$の範囲を動くとき、$Uはa=\displaystyle \frac{\boxed{\ \ ネ\ \ }}{\boxed{\ \ ノ\ \ }}$で
最大値$\displaystyle \frac{\boxed{\ \ ハ\ \ }}{\boxed{\ \ ヒフ\ \ }}$をとる。
2020センター試験過去問
この動画を見る
${\large第2問}$
$a \gt 0$とし、$f(x)=x^2-(4a-2)x+4a^2+1$ とおく。座標平面上で、放物線
$y=x^2+2x+1$ を$C,$放物線$y=f(x)$を$D$とする。また、$l$を$C$と$D$の両方に
接する直線とする。
(1)lの方程式を求めよう。
$l$と$C$は点$(t,$ $t^2+2t+1)$において接するとすると、$l$の方程式は
$y=\left(\boxed{\ \ ア\ \ }\ t+\boxed{\ \ イ\ \ }\right)\ x$$-t^2+\boxed{\ \ ウ\ \ }$ $\cdots$①
である。また、$l$と$D$は点$(s,$ $f(s))$において接するとすると、$l$の方程式は
$y=\left(\boxed{\ \ エ\ \ }\ s-\boxed{\ \ オ\ \ }\ +\boxed{\ \ カ\ \ }\right)\ x$$-s^2+\boxed{\ \ キ\ \ }\ a^2+\boxed{\ \ ク\ \ }$ $\cdots$②
である。ここで、①と②は同じ直線を表しているので、$t=\boxed{\ \ ケ\ \ },$
$s=\boxed{\ \ コ\ \ }\ a$が成り立つ。
したがって、$l$の方程式は$y=\boxed{\ \ サ\ \ }\ x+\boxed{\ \ シ\ \ }$である。
(2)二つの放物線$C,D$の交点のx座標は$\boxed{\ \ ス\ \ }$である。
$C$と直線$\ t,$および直線$x=\boxed{\ \ ス\ \ }$で囲まれた図形の面積を$S$とすると
$S=\displaystyle \frac{a^{\boxed{セ}}}{\boxed{\ \ ソ\ \ }}$である。
(3)$a \geqq \displaystyle \frac{1}{2}$とする。二つの放物線$C,D$と直線$l$で囲まれた図形の中で
$0 \leqq x \leqq 1$を満たす部分の面積$T$は、$a \gt \boxed{\ \ タ\ \ }$のとき、$a$の値によらず
$T=\displaystyle \frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$
であり、$\displaystyle \frac{1}{2} \leqq a \leqq \boxed{\ \ タ\ \ }$のとき
$T=-\boxed{\ \ テ\ \ }\ a^3+\boxed{\ \ ト\ \ }\ a^2$$-\boxed{\ \ ナ\ \ }\ a+\displaystyle \frac{\boxed{\ \ ニ\ \ }}{\boxed{\ \ ヌ\ \ }}$
である。
(4)次に、(2),(3)で定めた$S,T$に対して、$U=2T-3S$とおく。$a$が
$\displaystyle \frac{1}{2} \leqq a \leqq \boxed{\ \ タ\ \ }$の範囲を動くとき、$Uはa=\displaystyle \frac{\boxed{\ \ ネ\ \ }}{\boxed{\ \ ノ\ \ }}$で
最大値$\displaystyle \frac{\boxed{\ \ ハ\ \ }}{\boxed{\ \ ヒフ\ \ }}$をとる。
2020センター試験過去問
最速。2020年センター試験解説。福田の入試問題解説〜2020年センター試験IIB第1問〜三角関数、指数対数関数、図形と方程式

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#図形と方程式#三角関数#指数関数と対数関数#指数関数#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第1問}$
[1](1)$0 \leqq \theta \lt 2\pi$のとき
$\sin\theta \gt \sqrt3\cos\left(\theta-\displaystyle \frac{\pi}{3}\right)$ $\cdots$①
となる$\theta$の値の範囲を求めよう。
加法定理を用いると
$\sqrt3\cos\left(\theta-\frac{\pi}{3}\right)=$$\displaystyle\frac{\sqrt{\boxed{\ \ ア\ \ }}}{\boxed{\ \ イ\ \ }}\cos\theta+\displaystyle\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ イ\ \ }}\sin\theta$
である。よって、三角関数の合成を用いると、①は
$\sin\left(\theta+\displaystyle\frac{\pi}{\boxed{\ \ エ\ \ }}\right) \lt 0$
と変形できる。したがって、求める範囲は
$\displaystyle\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}\pi \lt \theta \lt \frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}\pi$
である。
(2)$0 \leqq \theta \leqq \displaystyle\frac{\pi}{2}$とし、$k$を実数とする。$\sin\theta$と$\cos\theta$は$x$の2次方程式
$25x^2-35x+k=0$の解であるとする。このとき、解と係数の関係に
より$\sin\theta+\cos\theta$と$\sin\theta\cos\theta$の値を考えれば、$k=\boxed{\ \ ケコ\ \ }$で
あることがわかる。
さらに、$\theta$が$\sin\theta \geqq \cos\theta$を満たすとすると、$\sin\theta=\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }},$
$\cos\theta=\displaystyle\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}$である。このとき、$\theta$は$\boxed{\ \ ソ\ \ }$を満たす。
$\boxed{\ \ ソ\ \ }$に当てはまるものを、次の⓪~⑤のうちから一つ選べ。
⓪$0 \leqq \theta \lt \displaystyle\frac{\pi}{12}$
①$\displaystyle\frac{\pi}{12} \leqq \theta \lt \displaystyle\frac{\pi}{6}$
②$\displaystyle\frac{\pi}{6} \leqq \theta \lt \displaystyle\frac{\pi}{4}$
③$\displaystyle\frac{\pi}{4} \leqq \theta \lt \displaystyle\frac{\pi}{3}$
④$\displaystyle\frac{\pi}{3} \leqq \theta \lt \displaystyle\frac{5}{12}\pi$
⑤$\displaystyle\frac{5}{12}\pi \leqq \theta \leqq \displaystyle\frac{\pi}{2}$
[2](1)$t$は正の実数であり、$t^{\displaystyle\frac{1}{3}}-t^{-\displaystyle\frac{1}{3}}=-3$を満たすとする。このとき
$t^{\displaystyle\frac{2}{3}}+t^{-\displaystyle\frac{2}{3}}=\boxed{\ \ タチ\ \ }$
である。さらに
$t^{\frac{1}{2}}+t^{-\frac{1}{2}}=\sqrt{\boxed{\ \ ツテ\ \ }}, $$t-t^{-1}=\boxed{\ \ トナニ\ \ }$
である。
(2)$x,y$は正の実数とする。連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
\log_3(x\sqrt y) \leqq 5 \cdots②\\
\log_{81}\frac{y}{x^3} \leqq 1 \cdots③
\end{array}
\right.
\end{eqnarray}$
について考える。
$X=\log_3x,$ $Y=\log_3y$とおくと、②は
$\boxed{\ \ ヌ\ \ }\ X+Y \leqq \boxed{\ \ ネノ\ \ }$ $\cdots$④
と変形でき、③は
$\boxed{\ \ ハ\ \ }\ X-Y \geqq \boxed{\ \ ヒフ\ \ }$ $\cdots$⑤
と変形できる。
$X,Y$が④と⑤を満たすとき、$Y$の取り得る最大の整数の値は
$\boxed{\ \ ヘ\ \ }$である。また、$x,y$が②,③と$\log_3y=\boxed{\ \ ヘ\ \ }$を同時に
満たすとき、xの取り得る最大の整数の値は$\boxed{\ \ ホ\ \ }$である。
2020センター試験過去問
この動画を見る
${\large第1問}$
[1](1)$0 \leqq \theta \lt 2\pi$のとき
$\sin\theta \gt \sqrt3\cos\left(\theta-\displaystyle \frac{\pi}{3}\right)$ $\cdots$①
となる$\theta$の値の範囲を求めよう。
加法定理を用いると
$\sqrt3\cos\left(\theta-\frac{\pi}{3}\right)=$$\displaystyle\frac{\sqrt{\boxed{\ \ ア\ \ }}}{\boxed{\ \ イ\ \ }}\cos\theta+\displaystyle\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ イ\ \ }}\sin\theta$
である。よって、三角関数の合成を用いると、①は
$\sin\left(\theta+\displaystyle\frac{\pi}{\boxed{\ \ エ\ \ }}\right) \lt 0$
と変形できる。したがって、求める範囲は
$\displaystyle\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}\pi \lt \theta \lt \frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}\pi$
である。
(2)$0 \leqq \theta \leqq \displaystyle\frac{\pi}{2}$とし、$k$を実数とする。$\sin\theta$と$\cos\theta$は$x$の2次方程式
$25x^2-35x+k=0$の解であるとする。このとき、解と係数の関係に
より$\sin\theta+\cos\theta$と$\sin\theta\cos\theta$の値を考えれば、$k=\boxed{\ \ ケコ\ \ }$で
あることがわかる。
さらに、$\theta$が$\sin\theta \geqq \cos\theta$を満たすとすると、$\sin\theta=\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }},$
$\cos\theta=\displaystyle\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}$である。このとき、$\theta$は$\boxed{\ \ ソ\ \ }$を満たす。
$\boxed{\ \ ソ\ \ }$に当てはまるものを、次の⓪~⑤のうちから一つ選べ。
⓪$0 \leqq \theta \lt \displaystyle\frac{\pi}{12}$
①$\displaystyle\frac{\pi}{12} \leqq \theta \lt \displaystyle\frac{\pi}{6}$
②$\displaystyle\frac{\pi}{6} \leqq \theta \lt \displaystyle\frac{\pi}{4}$
③$\displaystyle\frac{\pi}{4} \leqq \theta \lt \displaystyle\frac{\pi}{3}$
④$\displaystyle\frac{\pi}{3} \leqq \theta \lt \displaystyle\frac{5}{12}\pi$
⑤$\displaystyle\frac{5}{12}\pi \leqq \theta \leqq \displaystyle\frac{\pi}{2}$
[2](1)$t$は正の実数であり、$t^{\displaystyle\frac{1}{3}}-t^{-\displaystyle\frac{1}{3}}=-3$を満たすとする。このとき
$t^{\displaystyle\frac{2}{3}}+t^{-\displaystyle\frac{2}{3}}=\boxed{\ \ タチ\ \ }$
である。さらに
$t^{\frac{1}{2}}+t^{-\frac{1}{2}}=\sqrt{\boxed{\ \ ツテ\ \ }}, $$t-t^{-1}=\boxed{\ \ トナニ\ \ }$
である。
(2)$x,y$は正の実数とする。連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
\log_3(x\sqrt y) \leqq 5 \cdots②\\
\log_{81}\frac{y}{x^3} \leqq 1 \cdots③
\end{array}
\right.
\end{eqnarray}$
について考える。
$X=\log_3x,$ $Y=\log_3y$とおくと、②は
$\boxed{\ \ ヌ\ \ }\ X+Y \leqq \boxed{\ \ ネノ\ \ }$ $\cdots$④
と変形でき、③は
$\boxed{\ \ ハ\ \ }\ X-Y \geqq \boxed{\ \ ヒフ\ \ }$ $\cdots$⑤
と変形できる。
$X,Y$が④と⑤を満たすとき、$Y$の取り得る最大の整数の値は
$\boxed{\ \ ヘ\ \ }$である。また、$x,y$が②,③と$\log_3y=\boxed{\ \ ヘ\ \ }$を同時に
満たすとき、xの取り得る最大の整数の値は$\boxed{\ \ ホ\ \ }$である。
2020センター試験過去問
2020年センター試験数学IA, IIB【予備校講師が分析】

単元:
#大学入試過去問(数学)#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師:
Morite2 English Channel
問題文全文(内容文):
上岡駿介先生がセンター試験数学IA,IIBの解説をします。
解説を聞いて、復習の参考にしましょう!
この動画を見る
上岡駿介先生がセンター試験数学IA,IIBの解説をします。
解説を聞いて、復習の参考にしましょう!
最速。2020年センター試験解説。福田の入試問題解説〜2020年センター試験IA第3問〜場合の数、確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第3問}$
[1]次の$\boxed{\ \ ア\ \ },\ \boxed{\ \ イ\ \ }$に当てはまるものを、下の⓪~⑤のうちから
一つずつ選べ。ただし、解答の順序は問わない。
正しい記述は$\boxed{\ \ ア\ \ }$と$\boxed{\ \ イ\ \ }$である。
⓪1枚のコインを投げる試行を5回繰り返すとき、少なくとも1回は表が
出る確率をpとすると、$p \gt 0.95$である。
①袋の中に赤球と白球が合わせて8個入っている。球を1個取り出し、色
を調べてから袋に戻す試行を行う。この試行を5回繰り返したところ赤球
が3回出た。したがって、1回の試行で赤球が出る確率は$\displaystyle\frac{3}{5}$である。
②箱の中に「い」と書かれたカードが1枚、「ろ」と書かれたカードが2枚、
「は」と書かれたカードが2枚の合計5枚のカードが入っている。同時に
2枚カードを取り出すとき、書かれた文字が異なる確率は$\displaystyle\frac{4}{5}$である。
③コインの面を見て「オモテ(表)または「ウラ(裏)」とだけ発言するロボット
が2体ある。ただし、どちらのロボットも出た面に対して正しく発言
する確率が0.9、正しく発言しない確率が0.1であり、これら2体は互いに
影響されるされることなく発言するものとする。いま、ある人が1枚のコインを
投げる。出た面を見た2体が、ともに「オモテ」と発言した時に、実際に
表が出ている確率をpとすると、$p \leqq 0.9$である。
[2]1枚のコインを最大で5回投げるゲームを行う。このゲームでは、1回
投げるごとに表が出たら持ち点に2点を加え、裏が出たら持ち点に-1点を
加える。はじめの持ち点は0点とし、ゲーム終了のルールを次のように定める。
・持ち点が再び0点になった場合は、その時点で終了する。
・持ち点が再び0点にならない場合は、コインを5回投げ終わった時点で
終了する。
(1)コインを2回投げ終わって持ち点が-2点である確率は$\displaystyle\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$である。
また、コインを2回投げ終わって持ち点が1点である確率は
$\displaystyle\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$である。
(2)持ち点が再び0点になることが起こるのは、コインを$\boxed{\ \ キ\ \ }$回投げ
終わったときである。コインを$\boxed{\ \ キ\ \ }$回投げ終わって持ち点が0点になる
確率は$\displaystyle\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }}$である。
(3)ゲームが終了した時点で持ち点が4点である確率は$\displaystyle\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サシ\ \ }}$である。
(4)ゲームが終了した時点で持ち点が4点であるとき、コインを2回投げ
終わって持ち点が1点である条件付き確率は$\displaystyle\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}$である。
2020センター試験過去問
この動画を見る
${\large第3問}$
[1]次の$\boxed{\ \ ア\ \ },\ \boxed{\ \ イ\ \ }$に当てはまるものを、下の⓪~⑤のうちから
一つずつ選べ。ただし、解答の順序は問わない。
正しい記述は$\boxed{\ \ ア\ \ }$と$\boxed{\ \ イ\ \ }$である。
⓪1枚のコインを投げる試行を5回繰り返すとき、少なくとも1回は表が
出る確率をpとすると、$p \gt 0.95$である。
①袋の中に赤球と白球が合わせて8個入っている。球を1個取り出し、色
を調べてから袋に戻す試行を行う。この試行を5回繰り返したところ赤球
が3回出た。したがって、1回の試行で赤球が出る確率は$\displaystyle\frac{3}{5}$である。
②箱の中に「い」と書かれたカードが1枚、「ろ」と書かれたカードが2枚、
「は」と書かれたカードが2枚の合計5枚のカードが入っている。同時に
2枚カードを取り出すとき、書かれた文字が異なる確率は$\displaystyle\frac{4}{5}$である。
③コインの面を見て「オモテ(表)または「ウラ(裏)」とだけ発言するロボット
が2体ある。ただし、どちらのロボットも出た面に対して正しく発言
する確率が0.9、正しく発言しない確率が0.1であり、これら2体は互いに
影響されるされることなく発言するものとする。いま、ある人が1枚のコインを
投げる。出た面を見た2体が、ともに「オモテ」と発言した時に、実際に
表が出ている確率をpとすると、$p \leqq 0.9$である。
[2]1枚のコインを最大で5回投げるゲームを行う。このゲームでは、1回
投げるごとに表が出たら持ち点に2点を加え、裏が出たら持ち点に-1点を
加える。はじめの持ち点は0点とし、ゲーム終了のルールを次のように定める。
・持ち点が再び0点になった場合は、その時点で終了する。
・持ち点が再び0点にならない場合は、コインを5回投げ終わった時点で
終了する。
(1)コインを2回投げ終わって持ち点が-2点である確率は$\displaystyle\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$である。
また、コインを2回投げ終わって持ち点が1点である確率は
$\displaystyle\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$である。
(2)持ち点が再び0点になることが起こるのは、コインを$\boxed{\ \ キ\ \ }$回投げ
終わったときである。コインを$\boxed{\ \ キ\ \ }$回投げ終わって持ち点が0点になる
確率は$\displaystyle\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }}$である。
(3)ゲームが終了した時点で持ち点が4点である確率は$\displaystyle\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サシ\ \ }}$である。
(4)ゲームが終了した時点で持ち点が4点であるとき、コインを2回投げ
終わって持ち点が1点である条件付き確率は$\displaystyle\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}$である。
2020センター試験過去問
最速。2020年センター試験解説。福田の入試問題解説〜2020年センター試験IA第2問〜三角比、データの分析
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#データの分析#三角比への応用(正弦・余弦・面積)#データの分析#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第2問}$
[1]$\triangle ABC$において、$BC=2\sqrt2$とする。$\angle ACB$の二等分線と辺$AB$の交点
を$D$とし、$CD=\sqrt2,\cos\angle BCD=\displaystyle\frac{3}{4}$とする。このとき、$BD=\boxed{\ \ ア\ \ }$
であり、
$\sin\angle ADC=\frac{\sqrt{\boxed{\ \ イウ\ \ }}}{\boxed{\ \ エ\ \ }}$
である。$\displaystyle\frac{AC}{AD}=\sqrt{\boxed{\ \ オ\ \ }}$ であるから
$AD=\boxed{\ \ カ\ \ }$
である。また、$\triangle ABC$の外接円の半径は$\displaystyle\frac{\boxed{\ \ キ\ \ }\sqrt{\boxed{\ \ ク\ \ }}}{\boxed{\ \ ケ\ \ }}$ である。
[2](1)次の$\boxed{\ \ コ\ \ },\boxed{\ \ サ\ \ }$に当てはまるものを、下の⓪~⑤のうちから
一つずつ選べ。ただし、解答の順序は問わない。
99個の観測地からなるデータがある。四分位数について述べた記述
で、どのようなデータでも成り立つものは$\boxed{\ \ コ\ \ }$と$\boxed{\ \ サ\ \ }$である。
⓪平均値は第1四分位数と第3四分位数の間にある。
①四分位範囲は標準偏差より大きい。
②中央値よりっ地裁観測地の個数は49個である。
③最大値に等しい観測値を1個削除しても第1四分位数は変わらない。
④第1四分位数より小さい観測値と、第3四分位数より大きい観測値と
をすべて削除すると、残りの観測地の個数は51個である。
⑤第1四分位数より小さい観測値と、第3四分位数より大きい観測値と
をすべて削除すると、残りの観測地からなるデータの範囲はもとの
データの四分位範囲に等しい。
(2)図1(※動画参照)は、平成27年の男の市区町村別平均寿命のデータを47の都道府県
P1,P2,$\cdots$,P47ごとに箱ひげ図にして、並べたものである。
次の$(\textrm{I}),(\textrm{II}),(\textrm{III})$は図1に関する記述である。
$(\textrm{I})$四分位範囲はどの都道府県においても1以下である。
$(\textrm{II})$箱ひげ図は中央値が小さい値から大きい値の順に上から
下へ並んである。
$(\textrm{III})$P1のデータのどの値とP47のデータのどの値とを
比較しても1.5以上の差がある。
次の$\boxed{\ \ シ\ \ }$に当てはまるものを、下の⓪~⑦のうちから一つ選べ。
$(\textrm{I}),(\textrm{II}),(\textrm{III})$の正誤の組み合わせとして正しいものは$\boxed{\ \ シ\ \ }$である。
(※選択肢は動画参照)
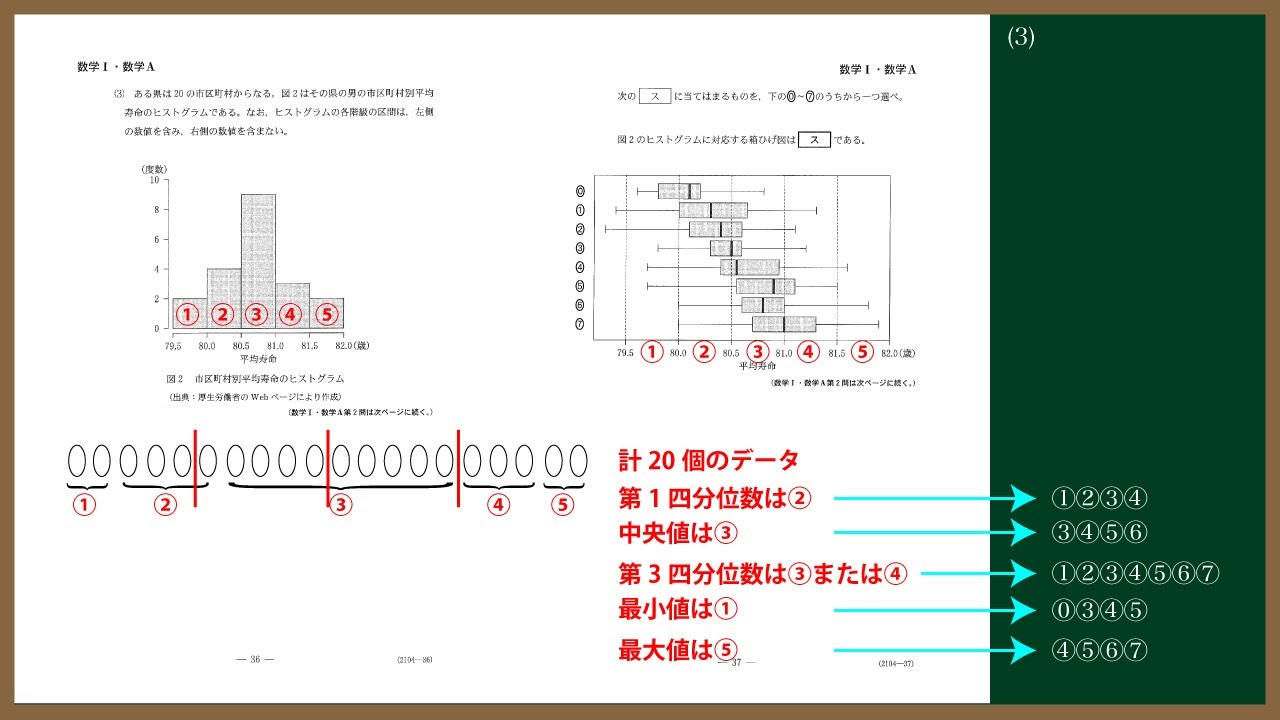
(3)ある県は20の市区町村からなる、図2(※動画参照)はその県の男の市区町村別平均
寿命のヒストグラムである。なお、ヒストグラムの各階級の区間は、左側の数値を
含み、右側の数値を含まない。
次の$\boxed{\ \ ス\ \ }$に当てはまるものを、下の⓪~⑦のうちから一つ選べ。
図2のヒストグラムに対応する箱ひげ図は$\boxed{\ \ ス\ \ }$である。
(※選択肢は動画参照)
(4)図3(※動画参照)は、平成27年の男の都道府県別平均寿命と女の都道府県別平均
寿命の散布図である。2個の点が重なって区別できないところは黒丸にしている。
図には補助的に切片が5.5から7.5まで0.5刻みで傾き1の直線を5本付加している。
次の$\boxed{\ \ セ\ \ }$に当てはまるものを、下の⓪~③のうちから一つ選べ。
都道府県ごとに男女の平均寿命の差をとったデータに対するヒストグラム
は$\boxed{\ \ セ\ \ }$である。なお、ヒストグラムの各階級の区間は、
左側の数値を含み、右側の数値を含まない。
(※選択肢は動画参照)
2020センター試験過去問
この動画を見る
${\large第2問}$
[1]$\triangle ABC$において、$BC=2\sqrt2$とする。$\angle ACB$の二等分線と辺$AB$の交点
を$D$とし、$CD=\sqrt2,\cos\angle BCD=\displaystyle\frac{3}{4}$とする。このとき、$BD=\boxed{\ \ ア\ \ }$
であり、
$\sin\angle ADC=\frac{\sqrt{\boxed{\ \ イウ\ \ }}}{\boxed{\ \ エ\ \ }}$
である。$\displaystyle\frac{AC}{AD}=\sqrt{\boxed{\ \ オ\ \ }}$ であるから
$AD=\boxed{\ \ カ\ \ }$
である。また、$\triangle ABC$の外接円の半径は$\displaystyle\frac{\boxed{\ \ キ\ \ }\sqrt{\boxed{\ \ ク\ \ }}}{\boxed{\ \ ケ\ \ }}$ である。
[2](1)次の$\boxed{\ \ コ\ \ },\boxed{\ \ サ\ \ }$に当てはまるものを、下の⓪~⑤のうちから
一つずつ選べ。ただし、解答の順序は問わない。
99個の観測地からなるデータがある。四分位数について述べた記述
で、どのようなデータでも成り立つものは$\boxed{\ \ コ\ \ }$と$\boxed{\ \ サ\ \ }$である。
⓪平均値は第1四分位数と第3四分位数の間にある。
①四分位範囲は標準偏差より大きい。
②中央値よりっ地裁観測地の個数は49個である。
③最大値に等しい観測値を1個削除しても第1四分位数は変わらない。
④第1四分位数より小さい観測値と、第3四分位数より大きい観測値と
をすべて削除すると、残りの観測地の個数は51個である。
⑤第1四分位数より小さい観測値と、第3四分位数より大きい観測値と
をすべて削除すると、残りの観測地からなるデータの範囲はもとの
データの四分位範囲に等しい。
(2)図1(※動画参照)は、平成27年の男の市区町村別平均寿命のデータを47の都道府県
P1,P2,$\cdots$,P47ごとに箱ひげ図にして、並べたものである。
次の$(\textrm{I}),(\textrm{II}),(\textrm{III})$は図1に関する記述である。
$(\textrm{I})$四分位範囲はどの都道府県においても1以下である。
$(\textrm{II})$箱ひげ図は中央値が小さい値から大きい値の順に上から
下へ並んである。
$(\textrm{III})$P1のデータのどの値とP47のデータのどの値とを
比較しても1.5以上の差がある。
次の$\boxed{\ \ シ\ \ }$に当てはまるものを、下の⓪~⑦のうちから一つ選べ。
$(\textrm{I}),(\textrm{II}),(\textrm{III})$の正誤の組み合わせとして正しいものは$\boxed{\ \ シ\ \ }$である。
(※選択肢は動画参照)
(3)ある県は20の市区町村からなる、図2(※動画参照)はその県の男の市区町村別平均
寿命のヒストグラムである。なお、ヒストグラムの各階級の区間は、左側の数値を
含み、右側の数値を含まない。
次の$\boxed{\ \ ス\ \ }$に当てはまるものを、下の⓪~⑦のうちから一つ選べ。
図2のヒストグラムに対応する箱ひげ図は$\boxed{\ \ ス\ \ }$である。
(※選択肢は動画参照)
(4)図3(※動画参照)は、平成27年の男の都道府県別平均寿命と女の都道府県別平均
寿命の散布図である。2個の点が重なって区別できないところは黒丸にしている。
図には補助的に切片が5.5から7.5まで0.5刻みで傾き1の直線を5本付加している。
次の$\boxed{\ \ セ\ \ }$に当てはまるものを、下の⓪~③のうちから一つ選べ。
都道府県ごとに男女の平均寿命の差をとったデータに対するヒストグラム
は$\boxed{\ \ セ\ \ }$である。なお、ヒストグラムの各階級の区間は、
左側の数値を含み、右側の数値を含まない。
(※選択肢は動画参照)
2020センター試験過去問
最速。2020年センター試験解説。福田の入試問題解説〜2020年センター試験IA第1問

単元:
#大学入試過去問(数学)#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第1問}$
[1]$a$を定数とする。
(1)直線$l:y=(a^2-2a-8)x+a$ の傾きが負となるのは、$a$の値の範囲が
$\boxed{\ \ アイ\ \ } \lt a \lt \boxed{\ \ ウ\ \ }$
のときである。
(2)$a^2-2a-8 \ne 0$とし、(1)の直線$l$と$x$軸との交点の$x$座標を$b$とする。
$a \gt 0$の場合、$b \gt 0$となるのは$\boxed{\ \ エ\ \ } \lt a \lt \boxed{\ \ オ\ \ }$のときである。
$a \leqq 0$の場合、$b \gt 0$となるのは$a \lt \boxed{\ \ カキ\ \ }$のときである。
また、$a=\sqrt3$のとき
$b=\frac{\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}-\boxed{\ \ コ\ \ }}{\boxed{\ \ サシ\ \ }}$
である。
[2]自然数$n$に関する三つの条件$p,q,r$を次のように定める。
$p:n$は$4$の倍数である
$q:n$は$6$の倍数である
$r:n$は$24$の倍数である
条件$p,q,r$の否定をそれぞれ$\bar{ p },\bar{ q },\bar{ r }$で表す。
条件$p$を満たす自然数全体の集合を$P$とし、条件$q$を満たす自然数全体
の集合を$Q$とし、条件$r$を満たす自然数全体の集合を$R$とする。自然数全体
の集合を全体集合とし、集合$P,Q,R$の補集合をそれぞれ$\bar{ P },\bar{ Q },\bar{ R }$で表す。
(1)次の$\boxed{\ \ ス\ \ }$に当てはまるものを、下の⓪~⑤のうちから一つ選べ。
$32 \in \boxed{\ \ ス\ \ }$である。
⓪$P \cap Q \cap R$ ①$P \cap Q \cap \bar{ R }$ ②$P \cap \bar{ Q }$
③$\bar{ P } \cap Q$ ④$\bar{ P } \cap \bar{ Q } \cap R$ ⑤$\bar{ P } \cap \bar{ Q } \cap \bar{ R }$
(2)次の$\boxed{\ \ タ\ \ }$に当てはまるものを、下の⓪~④のうちから一つ選べ。
$P \cap Q$に属する自然数のうち最小のものは$\boxed{\ \ セソ\ \ }$である。
また、$\boxed{\ \ セソ\ \ }\ \boxed{\ \ タ\ \ }\ R$である。
⓪= ①$\subset$ ②$\supset$ ③$\in$ ④$\notin$
(3)次の$\boxed{\ \ チ\ \ }$に当てはまるものを、下の⓪~③のうちから一つ選べ。
自然数$\boxed{\ \ セソ\ \ }$は、命題$\boxed{\ \ チ\ \ }$の反例である。
⓪「($p$かつ$q$) $\implies \bar{ r }$」 ①「($p$または$q$) $\implies \bar{ r }$」
②「$r \implies$ ($p$かつ$q$)」 ③「($p$かつ$q$) $\implies r$」
[3]$c$を定数とする。2次関数$y=x^2$のグラフを、2点$(c,0),$ $(c+4,0)$
を通るように平行移動して得られるグラフを$G$とする。
(1)$G$をグラフにもつ2次関数は、$c$を用いて
$y=x^2-2\left(c+\boxed{\ \ ツ\ \ }\right)\ x+$$c\left(c+\boxed{\ \ テ\ \ }\right)$
と表せる。
$2$点$(3,0),$ $(3,-3)$を両端とする線分と$G$が共有点をもつような
$c$の値の範囲は
$-\boxed{\ \ ト\ \ } \leqq c \leqq \boxed{\ \ ナ\ \ },$ $\boxed{\ \ ニ\ \ } \leqq c \leqq \boxed{\ \ ヌ\ \ }$
である。
(2)$\boxed{\ \ ニ\ \ } \leqq c \leqq \boxed{\ \ ヌ\ \ }$の場合を考える。$G$が点$(3,-1)$を通る
とき、$G$は2次関数$y=x^2$のグラフを$x$軸方向に$\boxed{\ \ ネ\ \ }+\sqrt{\boxed{\ \ ノ\ \ }}$。
$y$軸方向に$\boxed{\ \ ハヒ\ \ }$だけ平行移動したものである。また、このとき
$G$と$y$軸との交点の$y$座標は$\boxed{\ \ フ\ \ }+\boxed{\ \ ヘ\ \ }\sqrt{\boxed{\ \ ホ\ \ }}$である。
2020センター試験過去問
この動画を見る
${\large第1問}$
[1]$a$を定数とする。
(1)直線$l:y=(a^2-2a-8)x+a$ の傾きが負となるのは、$a$の値の範囲が
$\boxed{\ \ アイ\ \ } \lt a \lt \boxed{\ \ ウ\ \ }$
のときである。
(2)$a^2-2a-8 \ne 0$とし、(1)の直線$l$と$x$軸との交点の$x$座標を$b$とする。
$a \gt 0$の場合、$b \gt 0$となるのは$\boxed{\ \ エ\ \ } \lt a \lt \boxed{\ \ オ\ \ }$のときである。
$a \leqq 0$の場合、$b \gt 0$となるのは$a \lt \boxed{\ \ カキ\ \ }$のときである。
また、$a=\sqrt3$のとき
$b=\frac{\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}-\boxed{\ \ コ\ \ }}{\boxed{\ \ サシ\ \ }}$
である。
[2]自然数$n$に関する三つの条件$p,q,r$を次のように定める。
$p:n$は$4$の倍数である
$q:n$は$6$の倍数である
$r:n$は$24$の倍数である
条件$p,q,r$の否定をそれぞれ$\bar{ p },\bar{ q },\bar{ r }$で表す。
条件$p$を満たす自然数全体の集合を$P$とし、条件$q$を満たす自然数全体
の集合を$Q$とし、条件$r$を満たす自然数全体の集合を$R$とする。自然数全体
の集合を全体集合とし、集合$P,Q,R$の補集合をそれぞれ$\bar{ P },\bar{ Q },\bar{ R }$で表す。
(1)次の$\boxed{\ \ ス\ \ }$に当てはまるものを、下の⓪~⑤のうちから一つ選べ。
$32 \in \boxed{\ \ ス\ \ }$である。
⓪$P \cap Q \cap R$ ①$P \cap Q \cap \bar{ R }$ ②$P \cap \bar{ Q }$
③$\bar{ P } \cap Q$ ④$\bar{ P } \cap \bar{ Q } \cap R$ ⑤$\bar{ P } \cap \bar{ Q } \cap \bar{ R }$
(2)次の$\boxed{\ \ タ\ \ }$に当てはまるものを、下の⓪~④のうちから一つ選べ。
$P \cap Q$に属する自然数のうち最小のものは$\boxed{\ \ セソ\ \ }$である。
また、$\boxed{\ \ セソ\ \ }\ \boxed{\ \ タ\ \ }\ R$である。
⓪= ①$\subset$ ②$\supset$ ③$\in$ ④$\notin$
(3)次の$\boxed{\ \ チ\ \ }$に当てはまるものを、下の⓪~③のうちから一つ選べ。
自然数$\boxed{\ \ セソ\ \ }$は、命題$\boxed{\ \ チ\ \ }$の反例である。
⓪「($p$かつ$q$) $\implies \bar{ r }$」 ①「($p$または$q$) $\implies \bar{ r }$」
②「$r \implies$ ($p$かつ$q$)」 ③「($p$かつ$q$) $\implies r$」
[3]$c$を定数とする。2次関数$y=x^2$のグラフを、2点$(c,0),$ $(c+4,0)$
を通るように平行移動して得られるグラフを$G$とする。
(1)$G$をグラフにもつ2次関数は、$c$を用いて
$y=x^2-2\left(c+\boxed{\ \ ツ\ \ }\right)\ x+$$c\left(c+\boxed{\ \ テ\ \ }\right)$
と表せる。
$2$点$(3,0),$ $(3,-3)$を両端とする線分と$G$が共有点をもつような
$c$の値の範囲は
$-\boxed{\ \ ト\ \ } \leqq c \leqq \boxed{\ \ ナ\ \ },$ $\boxed{\ \ ニ\ \ } \leqq c \leqq \boxed{\ \ ヌ\ \ }$
である。
(2)$\boxed{\ \ ニ\ \ } \leqq c \leqq \boxed{\ \ ヌ\ \ }$の場合を考える。$G$が点$(3,-1)$を通る
とき、$G$は2次関数$y=x^2$のグラフを$x$軸方向に$\boxed{\ \ ネ\ \ }+\sqrt{\boxed{\ \ ノ\ \ }}$。
$y$軸方向に$\boxed{\ \ ハヒ\ \ }$だけ平行移動したものである。また、このとき
$G$と$y$軸との交点の$y$座標は$\boxed{\ \ フ\ \ }+\boxed{\ \ ヘ\ \ }\sqrt{\boxed{\ \ ホ\ \ }}$である。
2020センター試験過去問
高2生もセンター試験をやってみよう!【篠原好】

単元:
#センター試験・共通テスト関連#センター試験#その他#勉強法#その他
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
「高2生もセンター試験を試してほしい!」理由についてお話しています。
この動画を見る
「高2生もセンター試験を試してほしい!」理由についてお話しています。
センター前日のあなたへ。伝えたい言葉。ピンチの時に。【篠原好】

単元:
#センター試験・共通テスト関連#センター試験#その他#その他
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
センター前日のあなたへ伝えたい言葉
「諦めるな!」ということについてお話しています。
この動画を見る
センター前日のあなたへ伝えたい言葉
「諦めるな!」ということについてお話しています。
絶対にやってはいけない!センター試験でのNG5選!【篠原好】

単元:
#センター試験・共通テスト関連#センター試験#その他#その他
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
絶対にやってはいけない!
「センター試験でのNG5選」についてお話しています。
この動画を見る
絶対にやってはいけない!
「センター試験でのNG5選」についてお話しています。
ベストを出すための「あと20日」のメンタル調整術~センター9割の受験勉強法【篠原好】

単元:
#センター試験・共通テスト関連#センター試験#その他#勉強法#その他
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
センター試験まであと20日!
「ベストを出すためのメンタル調整術」についてお話しています。
この動画を見る
センター試験まであと20日!
「ベストを出すためのメンタル調整術」についてお話しています。
センター試験(追試)数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#センター試験・共通テスト関連#センター試験#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$C_1=2$
$C_{n+1}=-C_n+n^2+3$
(1)
$C_{25}-C_{23}$の値を求めよ。
(2)
$C_{25}$の値を求めよ。
出典:2004年センター試験 追試問題
この動画を見る
$C_1=2$
$C_{n+1}=-C_n+n^2+3$
(1)
$C_{25}-C_{23}$の値を求めよ。
(2)
$C_{25}$の値を求めよ。
出典:2004年センター試験 追試問題
センター試験レベル 広島県立大 三次式

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#センター試験・共通テスト関連#学校別大学入試過去問解説(数学)#センター試験#数学(高校生)#広島大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2+px+q=0$は2つの実数解$\alpha,\beta(\alpha \neq \beta)$をもつ。
$f(x)=x^3-9x+6$とすると$f(\alpha)=\beta,f(\beta)=\alpha$を満たす。
$p,q$を求めよ。
出典:1998年県立広島大学 過去問
この動画を見る
$x^2+px+q=0$は2つの実数解$\alpha,\beta(\alpha \neq \beta)$をもつ。
$f(x)=x^3-9x+6$とすると$f(\alpha)=\beta,f(\beta)=\alpha$を満たす。
$p,q$を求めよ。
出典:1998年県立広島大学 過去問
Mr 東北大 1浪1留院試落ち 人生各駅停車 さがらごうち

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
動画内の図を参照して求めよ
(1)
$AP$
(2)
$OD$
(3)
$\cos \angle OAD$
(4)
$AC$
(5)
$\triangle ABC$
この動画を見る
動画内の図を参照して求めよ
(1)
$AP$
(2)
$OD$
(3)
$\cos \angle OAD$
(4)
$AC$
(5)
$\triangle ABC$
【英語】センター試験 2017年 第2問A(1)~(5)

単元:
#大学入試過去問(数学)#センター試験・共通テスト関連#センター試験#数学(高校生)
教材:
#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
前置詞や形容詞を補語にする方法,比較の強調,最上級の強調,分詞構文に関して解説していきます.
この動画を見る
前置詞や形容詞を補語にする方法,比較の強調,最上級の強調,分詞構文に関して解説していきます.
2016年度 本試験 数学B 群数列の解き方復習!

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#センター試験・共通テスト関連#センター試験#数学(高校生)#数B
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
2016年度 本試験 数学B 群数列の解き方復習解説動画です
この動画を見る
2016年度 本試験 数学B 群数列の解き方復習解説動画です
センター試験 数学1A満点のもっちゃんがセンター数学やるよ

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2-5x+3=0$の2解を$\alpha, \beta$
(1)$\alpha^3,\beta^3$を解にもつ2次方程式
$x^2+px+q=0$ $p,q$の値
(2)$|\alpha-\beta|=m+d$
$(m$整数,$0 \leqq d \lt 1)$
$n \leqq 10d \lt n+1$ 整数$n$
過去問:センター試験
この動画を見る
$x^2-5x+3=0$の2解を$\alpha, \beta$
(1)$\alpha^3,\beta^3$を解にもつ2次方程式
$x^2+px+q=0$ $p,q$の値
(2)$|\alpha-\beta|=m+d$
$(m$整数,$0 \leqq d \lt 1)$
$n \leqq 10d \lt n+1$ 整数$n$
過去問:センター試験
【高校数学】2018年度センター試験・数学ⅡB・過去問解説~大問1の2指数・対数~【数学ⅡB】

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
2018年度センター試験・数学ⅡB・過去問解説動画です
この動画を見る
2018年度センター試験・数学ⅡB・過去問解説動画です
【高校数学】2018年度センター試験・数学ⅡB・過去問解説~大問1の1三角関数~【数学ⅡB】

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1) 1ラジアンとは、㋐のことである。
㋐に当てはまるものを、次の⓪~③のうちから一つ選べ。
⓪半径が1、面積が1の扇形の中心角の大きさ
①半径がx、面積が1の扇形の中心角の大きさ
②半径が1、張の長さが1の扇形の中心角の大きさ
③半径がx、弧の長さが1の扇形の中心角の大きさ
(2) 144°を弧度で表すと$\displaystyle \frac{㋑}{㋒}$xラジアンである。
また、$\displaystyle \frac{23}{12}$xラジアンを度で表すと[エオカ]である。
(3) $\displaystyle \frac{x}{2}$≦θ≦xの範囲で2sin(θ+$\displaystyle \frac{π}{5}$)-2cos(θ+$\displaystyle \frac{π}{30}$=1を満たすθの値を求めよう。
x=θ+$\displaystyle \frac{π}{5}$とおくと、①は2sin x-2cos(x-$\displaystyle \frac{π}{㋖}$=1と表せる。
加法定理を用いると、この式はsin x-$\sqrt{ ㋗ }$cos x=1となる。
さらに、三角関数の合成を用いるとsin(x-$\displaystyle \frac{π}{㋘}$)=$\displaystyle \frac{1}{㋙}$と変形できる。
x=θ+$\displaystyle \frac{π}{5}$、$\displaystyle \frac{π}{2}$≦θ≦πだから、θ=$\displaystyle \frac{㋚㋛}{㋜㋝}$πである。
この動画を見る
(1) 1ラジアンとは、㋐のことである。
㋐に当てはまるものを、次の⓪~③のうちから一つ選べ。
⓪半径が1、面積が1の扇形の中心角の大きさ
①半径がx、面積が1の扇形の中心角の大きさ
②半径が1、張の長さが1の扇形の中心角の大きさ
③半径がx、弧の長さが1の扇形の中心角の大きさ
(2) 144°を弧度で表すと$\displaystyle \frac{㋑}{㋒}$xラジアンである。
また、$\displaystyle \frac{23}{12}$xラジアンを度で表すと[エオカ]である。
(3) $\displaystyle \frac{x}{2}$≦θ≦xの範囲で2sin(θ+$\displaystyle \frac{π}{5}$)-2cos(θ+$\displaystyle \frac{π}{30}$=1を満たすθの値を求めよう。
x=θ+$\displaystyle \frac{π}{5}$とおくと、①は2sin x-2cos(x-$\displaystyle \frac{π}{㋖}$=1と表せる。
加法定理を用いると、この式はsin x-$\sqrt{ ㋗ }$cos x=1となる。
さらに、三角関数の合成を用いるとsin(x-$\displaystyle \frac{π}{㋘}$)=$\displaystyle \frac{1}{㋙}$と変形できる。
x=θ+$\displaystyle \frac{π}{5}$、$\displaystyle \frac{π}{2}$≦θ≦πだから、θ=$\displaystyle \frac{㋚㋛}{㋜㋝}$πである。
【数学I】センター2018 第3問 確率 !!解説!!

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【数学I】センター2018 第3問 確率 解説動画です
この動画を見る
【数学I】センター2018 第3問 確率 解説動画です
