新潟大学

【高校数学】新潟大学2023年の積分の問題をその場で解説しながら解いてみた！毎日積分90日目~47都道府県制覇への道~【㉝新潟】【毎日17時投稿】

単元： #大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#新潟大学#数Ⅲ

指導講師：理数個別チャンネル

問題文全文(内容文)：
【新潟大学 2023】

a, b

を正の数とし、座標平面上の曲線

C_{1} : y = e^{a x}, C_{2} : y = \sqrt{2 x - b}

を考える。次の問いに答えよ。
(1)関数

y = e^{a x}

,と関数

y = \sqrt{2 x - b}

の導関数を求めよ。
(2)曲線

C_{1}

と曲線

C_{2}

が1点

P

を共有し、その点において共通の接線をもつとする。この時,

b

と点

P

の座標を

a

を用いて表せ。
(3) (2)において、曲線

C_{1}

,曲線

C_{2}

,

x

軸,

y

軸で囲まれる図形の面積を

a

を用いて表せ。

この動画を見る　

大学入試問題#300　新潟大学2010　#定積分　#極限

単元： #大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#新潟大学

指導講師：ますただ

問題文全文(内容文)：

F (x) = \int_{0}^{x} \sqrt{1 + e^{2 t}} d t

のとき

lim_{x \to \infty} {F (x) - e^{x}}

を求めよ

出典：2010年新潟大学　入試問題

この動画を見る　

大学入試問題#251　新潟大学(2012)　#相加相乗平均

単元： #数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)#新潟大学

指導講師：ますただ

問題文全文(内容文)：

a, b, c, d

：正の実数

\frac{a + b + c + d}{4} ≧ \sqrt[4]{a b c d}

を示せ

出典：2012年新潟大学　入試問題

この動画を見る　

#51　大学入試問題　新潟大学(2020)　定積分【King propertyっぽいけど・・・】

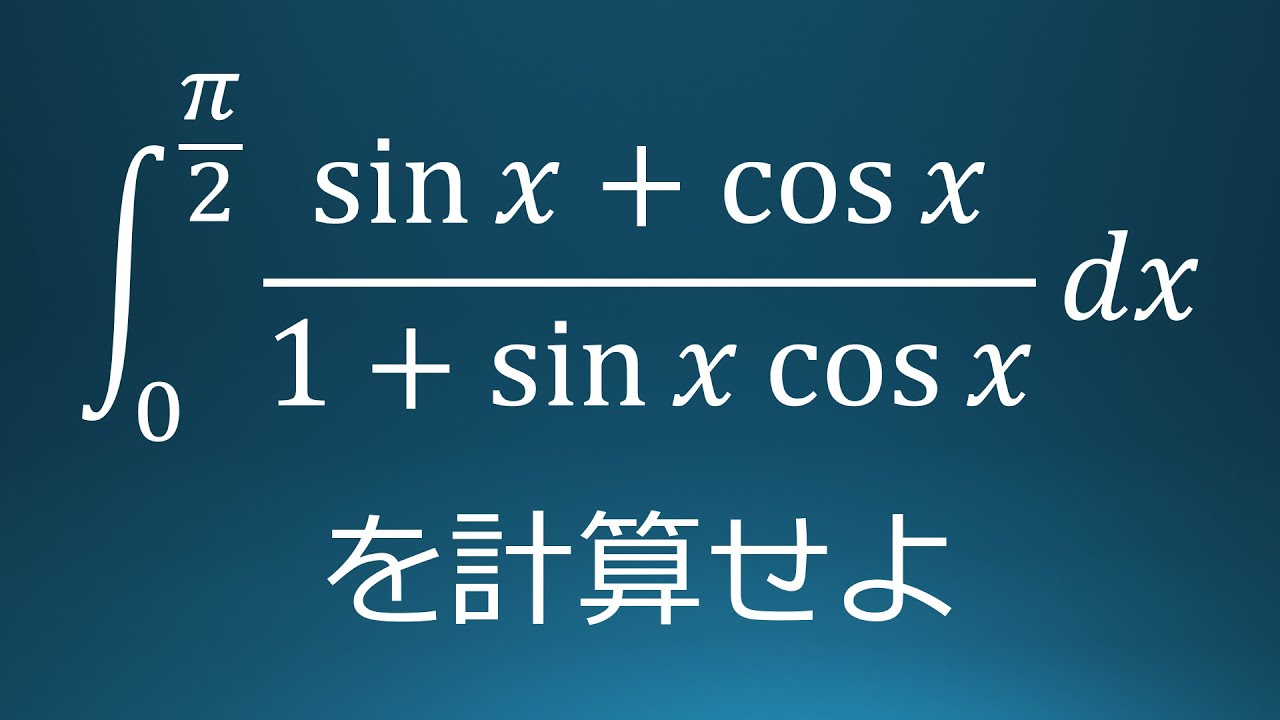
単元： #大学入試過去問(数学)#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#新潟大学#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：

\int_{0}^{\frac{π}{2}} \frac{\sin x + \cos x}{1 + \sin x \cos x} d x

を計算せよ。

出典：2020年新潟大学　入試問題

この動画を見る　

新潟大漸化式証明

単元： #大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#新潟大学#数B

指導講師：鈴木貫太郎

問題文全文(内容文)：

n

自然数

a_{n} = \sqrt{n^{2} + 1} - n

（1）

\frac{1}{2 n + 1} < a_{n} < \frac{1}{2 n}

を示せ

（2）

a_{n} > a_{n + 1}

を示せ

（3）

a_{n} < 0.03

となる最小の自然数

n

出典：2013年新潟大学　過去問

この動画を見る　

新潟大（医）３次関数・接線・面積 Mathematics Japanese university entrance exam

単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#新潟大学

指導講師：鈴木貫太郎

問題文全文(内容文)：

C : y = 2 x^{3} - 12 x

l : (1, - 2)

を通る

C

の接線

（1）

l

の方程式

（2）

C

と

l

とで囲まれた面積

出典：2006年新潟大学医学部　過去問

この動画を見る　

新潟大　漸化式 Mathematics Japanese university entrance exam

単元： #大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#新潟大学#数B

指導講師：鈴木貫太郎

問題文全文(内容文)：

a_{a + 2} = \frac{(a_{n + 1})^{3}}{(a_{n})^{2}}

a_{1} = 2

a_{2} = 4

一般項

a_{n}

を求めよ

出典：1996年新潟大学　過去問

この動画を見る　

新潟大　微分・積分 Mathematics Japanese university entrance exam

単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#数学(高校生)#新潟大学

指導講師：鈴木貫太郎

問題文全文(内容文)：
国立大学法人新潟大学

C :

f (x) = 2 x^{3} - 12 x

(1, - 2)

を通る接線

C

の接線を

l

(1) l

の方程式

(2) C

と

l

で囲まれる面積

この動画を見る　

新潟大　座標上の格子点の個数 Mathematics Japanese university entrance exam

単元： #大学入試過去問(数学)#微分とその応用#接線と法線・平均値の定理#学校別大学入試過去問解説(数学)#数学(高校生)#新潟大学#数Ⅲ

指導講師：鈴木貫太郎

問題文全文(内容文)：
'93新潟大学
n自然数

y = x^{2}

上の

(n, n^{2})

における接線をl

y = n^{2}

,l,及びy軸の3直線で囲まれた部分(境界含む)に含まれる格子点の数

この動画を見る　

新潟大　指数・対数 Mathematics Japanese university entrance exam

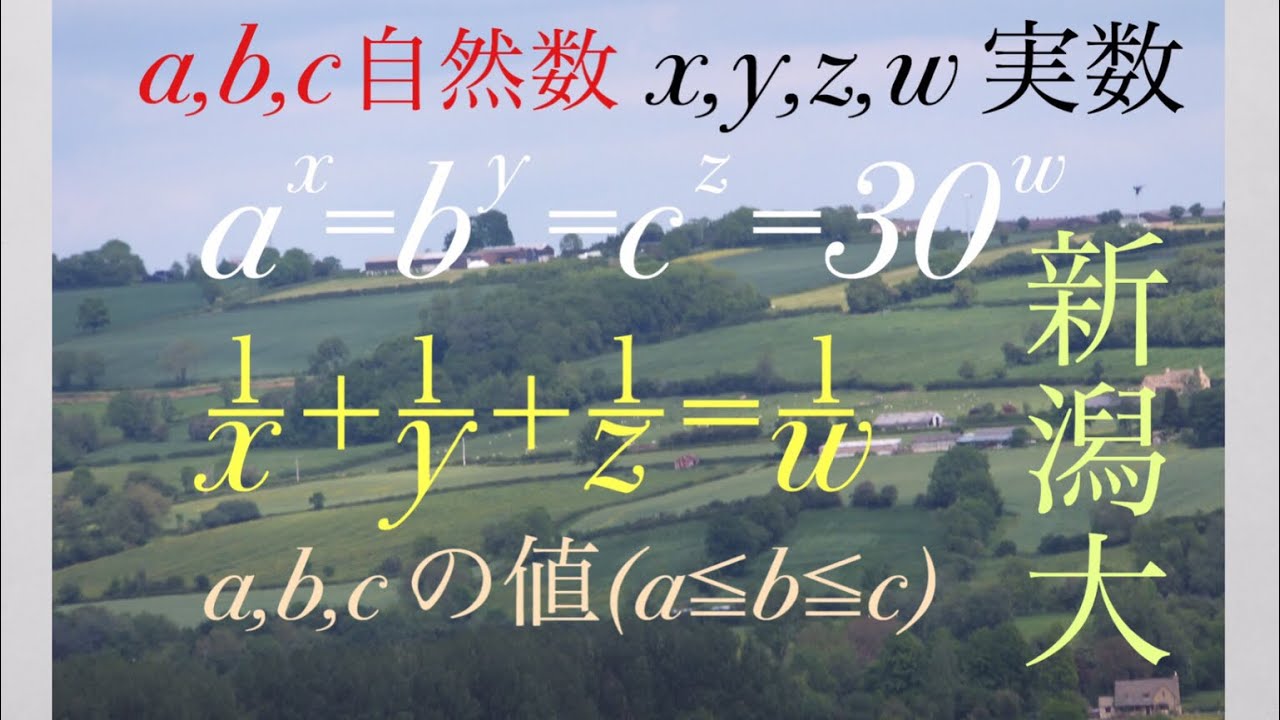
単元： #数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#新潟大学

指導講師：鈴木貫太郎

問題文全文(内容文)：
新潟大学過去問題
a,b,cは自然数
x,y,z,wは実数

a^{x} = b^{y} = c^{z} = 30^{w}

\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = \frac{1}{w}

を満たすとき、a,b,cを求めよ。

(a ≦ b ≦ c)

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> 新潟大学

【高校数学】新潟大学2023年の積分の問題をその場で解説しながら解いてみた！毎日積分90日目~47都道府県制覇への道~【㉝新潟】【毎日17時投稿】

大学入試問題#300 新潟大学2010 #定積分 #極限

大学入試問題#251 新潟大学(2012) #相加相乗平均

#51 大学入試問題 新潟大学(2020) 定積分【King propertyっぽいけど・・・】

新潟大 漸化式 証明

新潟大（医）３次関数・接線・面積 Mathematics Japanese university entrance exam

新潟大 漸化式 Mathematics Japanese university entrance exam

新潟大 微分・積分 Mathematics Japanese university entrance exam

新潟大 座標上の格子点の個数 Mathematics Japanese university entrance exam

新潟大 指数・対数 Mathematics Japanese university entrance exam

大学入試問題#300　新潟大学2010　#定積分　#極限

大学入試問題#251　新潟大学(2012)　#相加相乗平均

#51　大学入試問題　新潟大学(2020)　定積分【King propertyっぽいけど・・・】

新潟大漸化式証明

新潟大　漸化式 Mathematics Japanese university entrance exam

新潟大　微分・積分 Mathematics Japanese university entrance exam

新潟大　座標上の格子点の個数 Mathematics Japanese university entrance exam

新潟大　指数・対数 Mathematics Japanese university entrance exam