 慶應義塾大学
慶應義塾大学
 慶應義塾大学
慶應義塾大学
福田の数学〜2直線のなす角はtanの加法定理〜慶應義塾大学2023年商学部第2問〜2直線のなす角と面積

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a \gt 0,b \lt 0$とする。放物線C:$y=\dfrac{3}{2}x^2$上の点A(a,$\dfrac{3}{2}a^2$)と点B(b,$\dfrac{3}{2}b^2$)について、点Aと点Bにおける放物線の接線をそれぞれlとmで表し、その好転をPとする。
(1)lとmが直交するとき、交点Pのy座標は$-\dfrac{\fbox{ア}}{\fbox{イ}}$である。
(2)a=2で、$\angle APB=\dfrac{\pi}{4}$とする。このとき、bの値は$-\dfrac{\fbox{ウ}}{\fbox{エオ}}$である。
(3)b=-aで、$\angle APB=\dfrac{\pi}{3}$とする。この時、aの値は$\dfrac{\sqrt{\fbox{カ}}}{\fbox{キ}}$である。また、PAを半径、$\angle APB$を中心角として扇形PABが定まる。この扇形は放物線Cによって2つの図形に分割され、大きい図形の面積と小さい図形の面積の差は$\dfrac{\fbox{ク}}{\fbox{ケ}}\pi-\dfrac{\fbox{コ}\sqrt{\fbox{サ}}}{\fbox{シ}}$である。
2023慶應義塾大学商学部過去問
この動画を見る
$a \gt 0,b \lt 0$とする。放物線C:$y=\dfrac{3}{2}x^2$上の点A(a,$\dfrac{3}{2}a^2$)と点B(b,$\dfrac{3}{2}b^2$)について、点Aと点Bにおける放物線の接線をそれぞれlとmで表し、その好転をPとする。
(1)lとmが直交するとき、交点Pのy座標は$-\dfrac{\fbox{ア}}{\fbox{イ}}$である。
(2)a=2で、$\angle APB=\dfrac{\pi}{4}$とする。このとき、bの値は$-\dfrac{\fbox{ウ}}{\fbox{エオ}}$である。
(3)b=-aで、$\angle APB=\dfrac{\pi}{3}$とする。この時、aの値は$\dfrac{\sqrt{\fbox{カ}}}{\fbox{キ}}$である。また、PAを半径、$\angle APB$を中心角として扇形PABが定まる。この扇形は放物線Cによって2つの図形に分割され、大きい図形の面積と小さい図形の面積の差は$\dfrac{\fbox{ク}}{\fbox{ケ}}\pi-\dfrac{\fbox{コ}\sqrt{\fbox{サ}}}{\fbox{シ}}$である。
2023慶應義塾大学商学部過去問
福田の数学〜三角形の面積をxで表したいが〜慶應義塾大学2023年商学部第1問(3)〜三角比の図形への応用
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
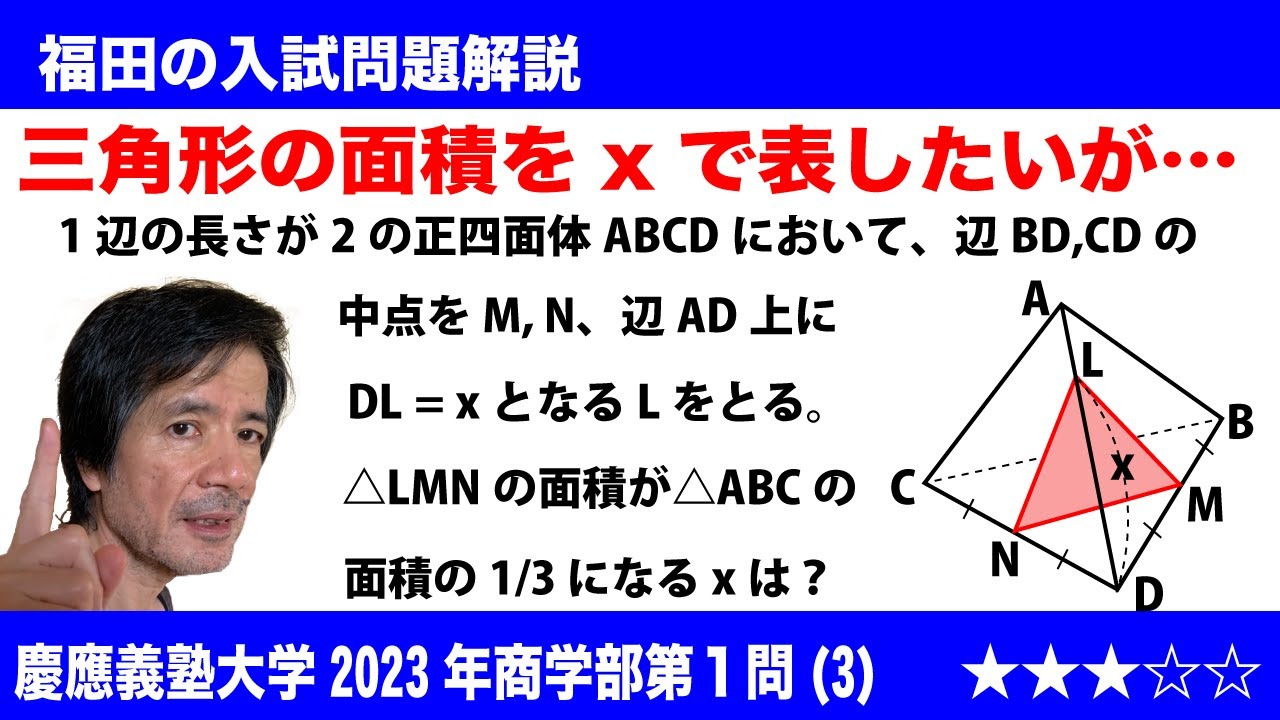
( 3 ) I 辺の長さが 2 の正四面体 ABCD において、辺 BD の中点を M 、辺 CD の中点を N とする。また、辺 AD 上に点 L を定め、 DL =xとする。このとき、$\triangle LMN$の面積が$\triangle ABC$の面積の$dfrac{1}{3}$になるのは$x=\dfrac{\fbox{ケ}}{\fbox{コ}}+\dfrac{\sqrt{\fbox{サシ}}}{ス}$のときである。
2023慶應義塾大学商学部過去問
この動画を見る
( 3 ) I 辺の長さが 2 の正四面体 ABCD において、辺 BD の中点を M 、辺 CD の中点を N とする。また、辺 AD 上に点 L を定め、 DL =xとする。このとき、$\triangle LMN$の面積が$\triangle ABC$の面積の$dfrac{1}{3}$になるのは$x=\dfrac{\fbox{ケ}}{\fbox{コ}}+\dfrac{\sqrt{\fbox{サシ}}}{ス}$のときである。
2023慶應義塾大学商学部過去問
福田の数学〜円と直線が共有点をもつ条件は〜慶應義塾大学2023年商学部第1問(2)〜円と直線の位置関係
単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(2)xy平面上において、点(4,3)を中心とする半径1の円とちょくせん$y=mx$が共有点を持つとき、
定数mの取り得る最大値は$\dfrac{\fbox{ウ}}{\fbox{エ}}+\dfrac{\fbox{オ}\sqrt{\fbox{カ}}}{\fbox{キク}}$である。
2023慶應義塾大学商学部過去問
この動画を見る
(2)xy平面上において、点(4,3)を中心とする半径1の円とちょくせん$y=mx$が共有点を持つとき、
定数mの取り得る最大値は$\dfrac{\fbox{ウ}}{\fbox{エ}}+\dfrac{\fbox{オ}\sqrt{\fbox{カ}}}{\fbox{キク}}$である。
2023慶應義塾大学商学部過去問
福田の数学〜対数関数の最大値2通りの解を紹介〜慶應義塾大学2023年商学部第1問(1)〜対数関数の最大値

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(1)2つの正の実数x,yについて、$xy^2=10$のとき、$\log_{ 10 } x$,$\log_{ 10 } y$の最大値は$\dfrac{\fbox{ア}}{{\fbox{イ}}}$である。
2023慶應義塾大学商学部過去問
この動画を見る
(1)2つの正の実数x,yについて、$xy^2=10$のとき、$\log_{ 10 } x$,$\log_{ 10 } y$の最大値は$\dfrac{\fbox{ア}}{{\fbox{イ}}}$である。
2023慶應義塾大学商学部過去問
福田の数学〜絶対落としたくないこの一題!〜慶應義塾大学2023年経済学部第6問〜定積分と面積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
a,bを実数の定数とする。また、xの関数$f(x)=x^3-ax+b$は
$a=\displaystyle \int_{-1}^{ 1 } \{\dfrac{3}{2}b|x^2+x|-f(x) \} dx$を満たすとする。
(1)bを、aを用いて表せ。
(2)y=f(x)で定まる曲線Cとx軸で囲まれた図形の面積Sを求めよ。なお、必要があれば$\alpha \lt \beta$を満たす実数$\alpha,\beta$に対して成り立つ公式
$a=\displaystyle \int_{\alpha}^{ \beta } (x-\alpha)^2(x-\beta) dx=-\dfrac{1}{12}(\beta-\alpha)^4$
を用いてもよい。
2023慶應義塾大学商学部過去問
この動画を見る
a,bを実数の定数とする。また、xの関数$f(x)=x^3-ax+b$は
$a=\displaystyle \int_{-1}^{ 1 } \{\dfrac{3}{2}b|x^2+x|-f(x) \} dx$を満たすとする。
(1)bを、aを用いて表せ。
(2)y=f(x)で定まる曲線Cとx軸で囲まれた図形の面積Sを求めよ。なお、必要があれば$\alpha \lt \beta$を満たす実数$\alpha,\beta$に対して成り立つ公式
$a=\displaystyle \int_{\alpha}^{ \beta } (x-\alpha)^2(x-\beta) dx=-\dfrac{1}{12}(\beta-\alpha)^4$
を用いてもよい。
2023慶應義塾大学商学部過去問
福田の数学〜立方体の平面による切断を考えよう〜慶應義塾大学2023年経済学部第5問〜立方体の平面による切断と体積の最大
単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
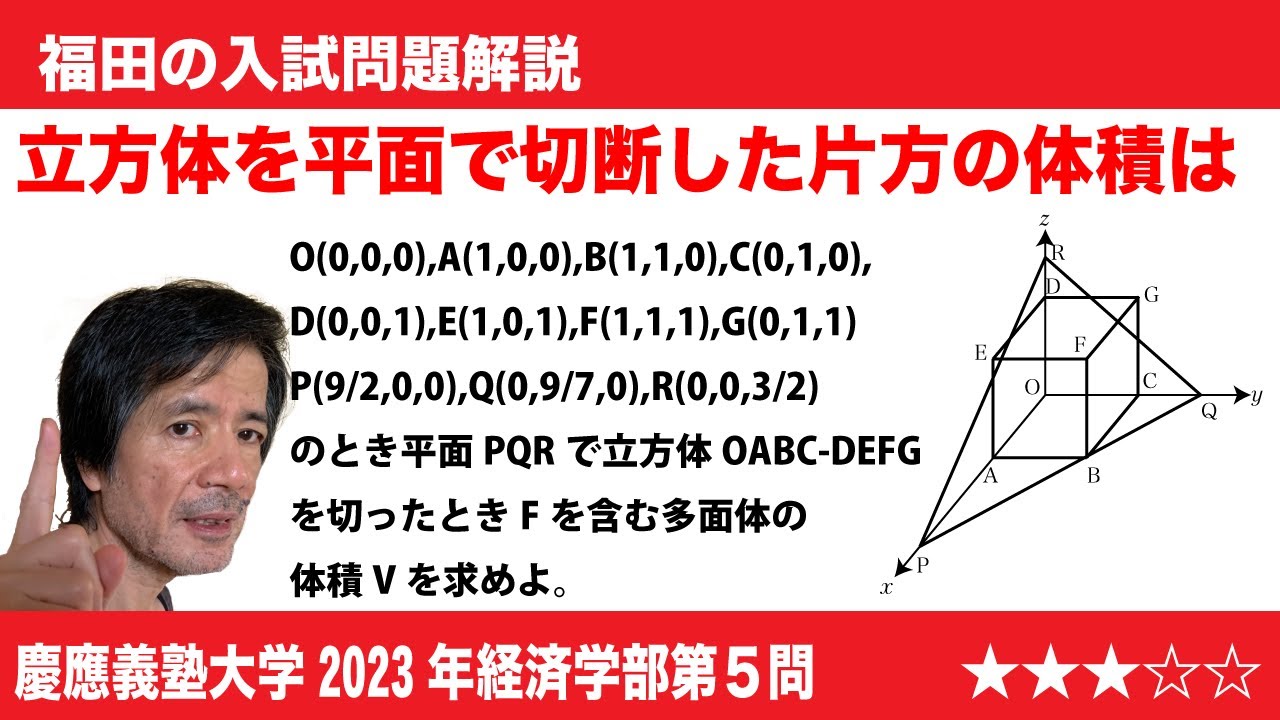
xyz空間における 8 点 O ( 0 , 0 , 0 ), A ( 1 , 0 , 0 ), B ( 1 , 1 , 0 ), C( 0 , 1 , 0 ), D ( 0 , 0 , 1 ),E ( 1 , 0 , 1 ), F( 1 , 1 , 1 ), G(0 , 1 , 1 ) を頂点とする立方体 OABC-DEFG を考える。また、pと q はp> 1 ,q> 1 を満たす実数とし、 3 点 P, Q, R を P( p, 0 , 0 ), Q(0 , q , 0 ),R( 0 , 0 , $\dfrac{3}{2}$ )とする。
(1)a,bを実数とし、べクトル$\vec{n}$=( a , b , 1 )は 2 つのべクトル $\overrightarrow{ PQ },\overrightarrow{ PR }$の両方に垂直であるとする。a,bをp,qを用いて表せ。
以下では 3 点 P, Q, R を通る平面を$\alpha$とし、点 F を通り平面を$\alpha$とし、点Fを通り平面$\alpha$に垂直な直線をlとする。また、xy平面と直線lの交点のx座標が$\dfrac{2}{3}$であるとし、点 B は線分 PQ 上にあるとする。
(2)pおよびqの値を求めよ。
( 3 )平面と線分 EF の交点 M の座標、および平面と直線 FG の交点 N の座標を求めよ。
( 4 )平面で立方体 OABC - DEFG を 2 つの多面体に切り分けたとき、点 F を含む多面体の体積Vを求めよ。
2023慶應義塾大学商学部過去問
この動画を見る
xyz空間における 8 点 O ( 0 , 0 , 0 ), A ( 1 , 0 , 0 ), B ( 1 , 1 , 0 ), C( 0 , 1 , 0 ), D ( 0 , 0 , 1 ),E ( 1 , 0 , 1 ), F( 1 , 1 , 1 ), G(0 , 1 , 1 ) を頂点とする立方体 OABC-DEFG を考える。また、pと q はp> 1 ,q> 1 を満たす実数とし、 3 点 P, Q, R を P( p, 0 , 0 ), Q(0 , q , 0 ),R( 0 , 0 , $\dfrac{3}{2}$ )とする。
(1)a,bを実数とし、べクトル$\vec{n}$=( a , b , 1 )は 2 つのべクトル $\overrightarrow{ PQ },\overrightarrow{ PR }$の両方に垂直であるとする。a,bをp,qを用いて表せ。
以下では 3 点 P, Q, R を通る平面を$\alpha$とし、点 F を通り平面を$\alpha$とし、点Fを通り平面$\alpha$に垂直な直線をlとする。また、xy平面と直線lの交点のx座標が$\dfrac{2}{3}$であるとし、点 B は線分 PQ 上にあるとする。
(2)pおよびqの値を求めよ。
( 3 )平面と線分 EF の交点 M の座標、および平面と直線 FG の交点 N の座標を求めよ。
( 4 )平面で立方体 OABC - DEFG を 2 つの多面体に切り分けたとき、点 F を含む多面体の体積Vを求めよ。
2023慶應義塾大学商学部過去問
福田の数学〜(2)から先行きが怪しくなってくる〜慶應義塾大学2023年経済学部第4問〜対数関数の最大

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
x,yを正の実数とし、$2\log_{ 2 } x+\log_{ 2 } y$とする。また、kを正の実数とする。
(1)x,yがx+y=kまたは、kx+y=2Kを満たすとする。このとき、zの取りうる値の最大値$z_1$及びその時のxの値を、Kを用いて表せ。
(2)x,yはx+y=KまたはKx+y=2Kを満たすとする。このとき、zの取りうる値の最大値$z_2$が(1)の$z_1$と一致するための必要十分条件を求めよ。
(3)nを自然数とし、$K=2^\frac{n}{5}$とする。(2)の$z_2$について、$\dfrac{3}{2} \lt z_2 \lt \dfrac{7}{2}$を満たす。
nの最大値および最小値を求めよ。必要があれば$1.58 \lt \log_{2}3 \lt 1.59$を用いよ。
2023慶應義塾大学経済学部過去問
この動画を見る
x,yを正の実数とし、$2\log_{ 2 } x+\log_{ 2 } y$とする。また、kを正の実数とする。
(1)x,yがx+y=kまたは、kx+y=2Kを満たすとする。このとき、zの取りうる値の最大値$z_1$及びその時のxの値を、Kを用いて表せ。
(2)x,yはx+y=KまたはKx+y=2Kを満たすとする。このとき、zの取りうる値の最大値$z_2$が(1)の$z_1$と一致するための必要十分条件を求めよ。
(3)nを自然数とし、$K=2^\frac{n}{5}$とする。(2)の$z_2$について、$\dfrac{3}{2} \lt z_2 \lt \dfrac{7}{2}$を満たす。
nの最大値および最小値を求めよ。必要があれば$1.58 \lt \log_{2}3 \lt 1.59$を用いよ。
2023慶應義塾大学経済学部過去問
福田の数学〜複雑な条件付き確率に挑戦しよう〜慶應義塾大学2023年経済学部第3問〜条件付き確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
[ 3 ]袋の中に、 1 から 9 までの数字を重複なく 1 つずっ記入したカ ー ドが 9 枚入ている。この袋からカ ー ドを 1 枚引き、カ ー ドに記入された数字を記録してから袋に戻すことを試行という。この試行を 5 回繰り返し行う。また、以下の (a), (b) に従い、各回の試行後の点数を定める。ただし、 1 回目の試行前の点数は 0 点とする。
(a) 各回の試行後、その回の試行で記録した数字と同じ数字のカ ー ドをそれまでに引いていない場合は、その回の試行前の点数にその回の試行で記録した数字を加える。
(b) 各回の試行後、その回の試行で記録した数字と同じ数字のカ ー ドをそれまでに引いている場合は、その回の試行前の点数にその回の試行で記録した数字を加え、さらに 1000 点を加える。
(1)3回の試行後の点数は23点であった。それまでに引いた3枚のカードに記入された数字は、小さい順に$\fbox{ア},\fbox{イ},\fbox{ウ}$である。これら3つの数字の文さんは$\dfrac{\fbox{エオ}}{\fbox{カ}}$である。
(2)4 回の試行後の点数が 23 点となる確率は$\dfrac{\fbox{キ}}{\fbox{クケコ}}$である。
(3)2 回の試行後の点数が 8 点または 1008点となる確率は$\dfrac{\fbox{サ}}{\fbox{シス}}$である。
(4)2 回の試行後の点数が 8 点または 1008 点であるとき、 5 回の試行後の点数が 2023 点となる条件付き確率は$\dfrac{\fbox{セソ}}{\fbox{タチツテ}}$である。
2023慶應義塾大学経済学部過去問
この動画を見る
[ 3 ]袋の中に、 1 から 9 までの数字を重複なく 1 つずっ記入したカ ー ドが 9 枚入ている。この袋からカ ー ドを 1 枚引き、カ ー ドに記入された数字を記録してから袋に戻すことを試行という。この試行を 5 回繰り返し行う。また、以下の (a), (b) に従い、各回の試行後の点数を定める。ただし、 1 回目の試行前の点数は 0 点とする。
(a) 各回の試行後、その回の試行で記録した数字と同じ数字のカ ー ドをそれまでに引いていない場合は、その回の試行前の点数にその回の試行で記録した数字を加える。
(b) 各回の試行後、その回の試行で記録した数字と同じ数字のカ ー ドをそれまでに引いている場合は、その回の試行前の点数にその回の試行で記録した数字を加え、さらに 1000 点を加える。
(1)3回の試行後の点数は23点であった。それまでに引いた3枚のカードに記入された数字は、小さい順に$\fbox{ア},\fbox{イ},\fbox{ウ}$である。これら3つの数字の文さんは$\dfrac{\fbox{エオ}}{\fbox{カ}}$である。
(2)4 回の試行後の点数が 23 点となる確率は$\dfrac{\fbox{キ}}{\fbox{クケコ}}$である。
(3)2 回の試行後の点数が 8 点または 1008点となる確率は$\dfrac{\fbox{サ}}{\fbox{シス}}$である。
(4)2 回の試行後の点数が 8 点または 1008 点であるとき、 5 回の試行後の点数が 2023 点となる条件付き確率は$\dfrac{\fbox{セソ}}{\fbox{タチツテ}}$である。
2023慶應義塾大学経済学部過去問
福田の数学〜部分和と漸化式の扱い方〜慶應義塾大学2023年経済学部第2問〜部分和と漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数列$\{a_{n}\}$に対して$\displaystyle \sum_{k=1}^n a_k(n=1,2,3,・・・)$とし、さらに$S_0=0$と定める。$\{a_n\}$は$S_n=\dfrac{1}{4}-\dfrac{1}{2}(n+3)a_{n+1}$(n=0,1,2,・・・)を満たすとする。
(1)$a_1=\dfrac{\fbox{ア}}{\fbox{イ}}$である。また、$n \geqq 1$に対して$a_n=S_n-S_{n-1}$であるから、関係式$(n+\fbox{ウ})a_{n+1}=(n+\fbox{エ})a_n (n=1,2,3,・・・)$・・・(*)が得られる。数列$\{{b_n}\}$を$b_n=n(n+1)(n+2)a_n (n=1,2,3,・・・)$で定めると、$b_1=\fbox{オ}$であり、$n \geqq 1$に対して$b_{n+1}=\fbox{カ}b_n$が成り立つ。ゆえに$a_n=\dfrac{\fbox{キ}}{n(n+1)(n+2)}$が得られる。
次に、数列$\{{T_n}\}=\displaystyle \sum_{k=1}^n \dfrac{a_k}{(k+3)(k+4)}(n=1,2,3,・・・)$で定める。
(2)(*)より導かれる関係式
$\dfrac{a_k}{k+3}-\dfrac{a_{k+1}}{k+4}=\dfrac{\fbox{ク}a_k}{(k+3)(k+4)} (k=1,2,3,・・・)$
を用いると
$T_n=A-\dfrac{\fbox{ケ}}{\fbox{コ}(n+p)(n+q)(n+r)(n+s)}(n=1,2,3,・・・)$
が得られる。ただしここに$A=\fbox{サ}{シス}$であり、$p \lt q\lt r \lt s$として$p=\fbox{セ},q=\fbox{ソ},r=\fbox{タ},s=\fbox{チ}$である。
(3)不等式$|T_n-A| \lt\dfrac{1}{10000(n+1)(n+2)}$を満たす最小の自然数$nはn=\fbox{ツテ}$である。
2023慶應義塾大学経済学部過去問
この動画を見る
数列$\{a_{n}\}$に対して$\displaystyle \sum_{k=1}^n a_k(n=1,2,3,・・・)$とし、さらに$S_0=0$と定める。$\{a_n\}$は$S_n=\dfrac{1}{4}-\dfrac{1}{2}(n+3)a_{n+1}$(n=0,1,2,・・・)を満たすとする。
(1)$a_1=\dfrac{\fbox{ア}}{\fbox{イ}}$である。また、$n \geqq 1$に対して$a_n=S_n-S_{n-1}$であるから、関係式$(n+\fbox{ウ})a_{n+1}=(n+\fbox{エ})a_n (n=1,2,3,・・・)$・・・(*)が得られる。数列$\{{b_n}\}$を$b_n=n(n+1)(n+2)a_n (n=1,2,3,・・・)$で定めると、$b_1=\fbox{オ}$であり、$n \geqq 1$に対して$b_{n+1}=\fbox{カ}b_n$が成り立つ。ゆえに$a_n=\dfrac{\fbox{キ}}{n(n+1)(n+2)}$が得られる。
次に、数列$\{{T_n}\}=\displaystyle \sum_{k=1}^n \dfrac{a_k}{(k+3)(k+4)}(n=1,2,3,・・・)$で定める。
(2)(*)より導かれる関係式
$\dfrac{a_k}{k+3}-\dfrac{a_{k+1}}{k+4}=\dfrac{\fbox{ク}a_k}{(k+3)(k+4)} (k=1,2,3,・・・)$
を用いると
$T_n=A-\dfrac{\fbox{ケ}}{\fbox{コ}(n+p)(n+q)(n+r)(n+s)}(n=1,2,3,・・・)$
が得られる。ただしここに$A=\fbox{サ}{シス}$であり、$p \lt q\lt r \lt s$として$p=\fbox{セ},q=\fbox{ソ},r=\fbox{タ},s=\fbox{チ}$である。
(3)不等式$|T_n-A| \lt\dfrac{1}{10000(n+1)(n+2)}$を満たす最小の自然数$nはn=\fbox{ツテ}$である。
2023慶應義塾大学経済学部過去問
福田の数学〜不定方程式の自然数解を求めよう〜慶應義塾大学2023年経済学部第1問(2)〜点対称と不定方程式の自然数解

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
( 2 ) m,nを自然数とし、pを実数とする。平面上の点$(p,/\dfrac{p}{2})$に関して点(m,n)と対称な点が$(-3m^2-4mn+5m,n^2-3n-3)$であるとき、関係式$\fbox{ス}m^2+2(\fbox{セ}n-\fbox{ソ}m)+2(n+\fbox{タ})(n-\fbox{チ})=0$
が成り立つ。ゆえに$m=\fbox{ツ},n=\fbox{テ},p=\fbox{トナ}$である。
2023慶應義塾大学経済学部過去問
この動画を見る
( 2 ) m,nを自然数とし、pを実数とする。平面上の点$(p,/\dfrac{p}{2})$に関して点(m,n)と対称な点が$(-3m^2-4mn+5m,n^2-3n-3)$であるとき、関係式$\fbox{ス}m^2+2(\fbox{セ}n-\fbox{ソ}m)+2(n+\fbox{タ})(n-\fbox{チ})=0$
が成り立つ。ゆえに$m=\fbox{ツ},n=\fbox{テ},p=\fbox{トナ}$である。
2023慶應義塾大学経済学部過去問
大学入試問題#652「パット見余裕!」 慶應大学医学部(2001) 整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\sqrt{ n^2+n+34 }$が整数となるような自然数$n$をすべて求めよ
出典:2001年慶應義塾大学 入試問題
この動画を見る
$\sqrt{ n^2+n+34 }$が整数となるような自然数$n$をすべて求めよ
出典:2001年慶應義塾大学 入試問題
福田の数学〜三角比の基本の復習にどうぞ〜慶應義塾大学2023年経済学部第1問(1)〜三角形と外接円内接円の半径

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(1)$\triangle ABC$において
$sinA:sinB:sinC=3:7:8$
が成り立つとき、ある性の実数kを用いて
$a=\fbox{ア}k,b=\fbox{イ}k,c=\fbox{ウ}k$
と表すことができるので、この三角形の最も大きい角の余弦の値は$-\dfrac{\fbox{エ}}{\fbox{オ}}$であり、正弦の値は$-\fbox{カ}\sqrt{\fbox{キ}}$である。さらに$\triangle ABC$の面積が$54\sqrt{3}$であるとき、$k=\fbox{ク}$となるので、この三角形の外接円の半径は$\fbox{ケ}\sqrt{\fbox{コ}}$であり、内接円の半径は$\fbox{サ}\sqrt{\fbox{シ}}$である。
2023慶應義塾大学経済学部過去問
この動画を見る
(1)$\triangle ABC$において
$sinA:sinB:sinC=3:7:8$
が成り立つとき、ある性の実数kを用いて
$a=\fbox{ア}k,b=\fbox{イ}k,c=\fbox{ウ}k$
と表すことができるので、この三角形の最も大きい角の余弦の値は$-\dfrac{\fbox{エ}}{\fbox{オ}}$であり、正弦の値は$-\fbox{カ}\sqrt{\fbox{キ}}$である。さらに$\triangle ABC$の面積が$54\sqrt{3}$であるとき、$k=\fbox{ク}$となるので、この三角形の外接円の半径は$\fbox{ケ}\sqrt{\fbox{コ}}$であり、内接円の半径は$\fbox{サ}\sqrt{\fbox{シ}}$である。
2023慶應義塾大学経済学部過去問
福田の数学〜慶應義塾大学2023年理工学部第5問(2)〜不定方程式の整数解

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ (2)$f(x)$=$x-$$\displaystyle\frac{1}{x}$とする。自然数$a$,$b$,$c$の組で$a$≦$b$≦$c$かつ$f(a)$+$f(b)$+$f(c)$が自然数であるものの総数は$\boxed{\ \ ト\ \ }$個である。その中で$f(a)$+$f(b)$+$f(c)$の値が最大になるのは($a$,$b$,$c$)=$\boxed{\ \ ナ\ \ }$のときである。
この動画を見る
$\Large\boxed{5}$ (2)$f(x)$=$x-$$\displaystyle\frac{1}{x}$とする。自然数$a$,$b$,$c$の組で$a$≦$b$≦$c$かつ$f(a)$+$f(b)$+$f(c)$が自然数であるものの総数は$\boxed{\ \ ト\ \ }$個である。その中で$f(a)$+$f(b)$+$f(c)$の値が最大になるのは($a$,$b$,$c$)=$\boxed{\ \ ナ\ \ }$のときである。
福田の数学〜慶應義塾大学2023年理工学部第5問(1)〜複素数平面上の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ (1)$\alpha$を±1ではない複素数とする。複素数平面上で$\displaystyle\left|\frac{\alpha z+1}{z+\alpha}\right|$=2 を満たす点$z$全体からなる図形を$C$とする。$C$は$\alpha$が$\boxed{\ \ チ\ \ }$を満たすとき直線となり、$\boxed{\ \ チ\ \ }$を満たさないとき円となる。$\alpha$が$\boxed{\ \ チ\ \ }$を満たさないとき、円$C$の中心を$\alpha$を用いて表すと$\boxed{\ \ ツ\ \ }$となる。$\alpha$が$\boxed{\ \ チ\ \ }$を満たすとき、直線$C$上の点$z$のうち、
その絶対値が最小となるものを$\alpha$を用いて表すと$\boxed{\ \ テ\ \ }$となる。
この動画を見る
$\Large\boxed{5}$ (1)$\alpha$を±1ではない複素数とする。複素数平面上で$\displaystyle\left|\frac{\alpha z+1}{z+\alpha}\right|$=2 を満たす点$z$全体からなる図形を$C$とする。$C$は$\alpha$が$\boxed{\ \ チ\ \ }$を満たすとき直線となり、$\boxed{\ \ チ\ \ }$を満たさないとき円となる。$\alpha$が$\boxed{\ \ チ\ \ }$を満たさないとき、円$C$の中心を$\alpha$を用いて表すと$\boxed{\ \ ツ\ \ }$となる。$\alpha$が$\boxed{\ \ チ\ \ }$を満たすとき、直線$C$上の点$z$のうち、
その絶対値が最小となるものを$\alpha$を用いて表すと$\boxed{\ \ テ\ \ }$となる。
福田の数学〜慶應義塾大学2023年理工学部第4問〜定積分と不等式Part2
単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ (1)0≦$x$≦$\displaystyle\frac{\pi}{2}$において常に不等式|$b$|≦|$b$+1-$b\cos x$|が成り立つような実数$b$の値の範囲は$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$である。
以下、$b$を$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$を満たす0でない実数とし、数列$\left\{a_n\right\}$を
$a_n$=$\displaystyle\int_0^{\frac{\pi}{2}}\frac{\sin x(\cos x)^{n-1}}{(b+1-b\cos x)^n}dx$ (n=1,2,3,...)で定義する。
(2)$\displaystyle\lim_{n \to \infty}b^na_n$=0 が成り立つことを証明しなさい。
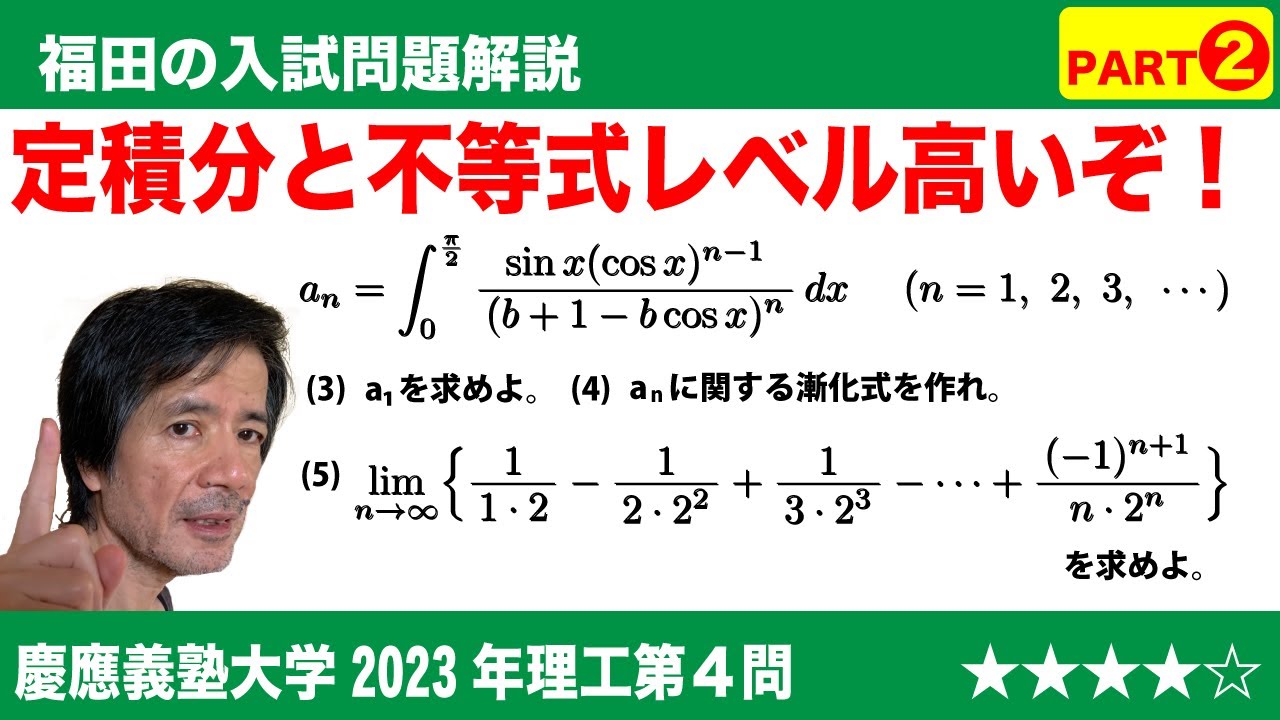
(3)$a_1$=$\boxed{\ \ セ\ \ }$である。
(4)$a_{n+1}$を$a_n$,$n$,$b$を用いて表すと$a_{n+1}$=$\boxed{\ \ ソ\ \ }$となる。
(5)$\displaystyle\lim_{n \to \infty}\left\{\frac{1}{1・2}-\frac{1}{2・2^2}+\frac{1}{3・2^3}-...+\frac{(-1)^{n+1}}{n・2^n}\right\}$=$\boxed{\ \ タ\ \ }$である。
この動画を見る
$\Large\boxed{4}$ (1)0≦$x$≦$\displaystyle\frac{\pi}{2}$において常に不等式|$b$|≦|$b$+1-$b\cos x$|が成り立つような実数$b$の値の範囲は$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$である。
以下、$b$を$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$を満たす0でない実数とし、数列$\left\{a_n\right\}$を
$a_n$=$\displaystyle\int_0^{\frac{\pi}{2}}\frac{\sin x(\cos x)^{n-1}}{(b+1-b\cos x)^n}dx$ (n=1,2,3,...)で定義する。
(2)$\displaystyle\lim_{n \to \infty}b^na_n$=0 が成り立つことを証明しなさい。
(3)$a_1$=$\boxed{\ \ セ\ \ }$である。
(4)$a_{n+1}$を$a_n$,$n$,$b$を用いて表すと$a_{n+1}$=$\boxed{\ \ ソ\ \ }$となる。
(5)$\displaystyle\lim_{n \to \infty}\left\{\frac{1}{1・2}-\frac{1}{2・2^2}+\frac{1}{3・2^3}-...+\frac{(-1)^{n+1}}{n・2^n}\right\}$=$\boxed{\ \ タ\ \ }$である。
福田の数学〜慶應義塾大学2023年理工学部第4問〜定積分と不等式Part1

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ (1)0≦$x$≦$\displaystyle\frac{\pi}{2}$において常に不等式|$b$|≦|$b$+1-$b\cos x$|が成り立つような実数$b$の値の範囲は$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$である。
以下、$b$を$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$を満たす0でない実数とし、数列$\left\{a_n\right\}$を
$a_n$=$\displaystyle\int_0^{\frac{\pi}{2}}\frac{\sin x(\cos x)^{n-1}}{(b+1-b\cos x)^n}dx$ (n=1,2,3,...)で定義する。
(2)$\displaystyle\lim_{n \to \infty}b^na_n$=0 が成り立つことを証明しなさい。
(3)$a_1$=$\boxed{\ \ セ\ \ }$である。
(4)$a_{n+1}$を$a_n$,$n$,$b$を用いて表すと$a_{n+1}$=$\boxed{\ \ ソ\ \ }$となる。
(5)$\displaystyle\lim_{n \to \infty}\left\{\frac{1}{1・2}-\frac{1}{2・2^2}+\frac{1}{3・2^3}-...+\frac{(-1)^{n+1}}{n・2^n}\right\}$=$\boxed{\ \ タ\ \ }$である。
この動画を見る
$\Large\boxed{4}$ (1)0≦$x$≦$\displaystyle\frac{\pi}{2}$において常に不等式|$b$|≦|$b$+1-$b\cos x$|が成り立つような実数$b$の値の範囲は$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$である。
以下、$b$を$\boxed{\ \ シ\ \ }$≦$b$≦$\boxed{\ \ ス\ \ }$を満たす0でない実数とし、数列$\left\{a_n\right\}$を
$a_n$=$\displaystyle\int_0^{\frac{\pi}{2}}\frac{\sin x(\cos x)^{n-1}}{(b+1-b\cos x)^n}dx$ (n=1,2,3,...)で定義する。
(2)$\displaystyle\lim_{n \to \infty}b^na_n$=0 が成り立つことを証明しなさい。
(3)$a_1$=$\boxed{\ \ セ\ \ }$である。
(4)$a_{n+1}$を$a_n$,$n$,$b$を用いて表すと$a_{n+1}$=$\boxed{\ \ ソ\ \ }$となる。
(5)$\displaystyle\lim_{n \to \infty}\left\{\frac{1}{1・2}-\frac{1}{2・2^2}+\frac{1}{3・2^3}-...+\frac{(-1)^{n+1}}{n・2^n}\right\}$=$\boxed{\ \ タ\ \ }$である。
福田の数学〜慶應義塾大学2023年理工学部第3問〜確率と漸化式(難問)Part3

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 何も入っていない2つの袋A,Bがある。いま、「硬貨を1枚投げて表が出たら袋A、裏が出たら袋Bを選び、以下のルールに従って選んだ袋の中に玉を入れる」
という操作を繰り返す。
ルール
・選んだ袋の中に入っている玉の数がもう一方の袋の中に入っている玉の数より多いか、2つの袋の中に入っている玉の数が同じとき、選んだ袋の中に玉を1個入れる。
・選んだ袋の中に入っている玉の数がもう一方の袋の中に入っている玉の数より少ないとき、選んだ袋の中に入っている玉の数が、もう一方の袋の中に入っている玉の数と同じになるまで選んだ袋の中に玉をいれる。
たとえば、上の操作を3回行ったとき、硬貨が順に表、表、裏と出たとすると、
A,B2つの袋の中の玉の数は次のように変化する。
A:0個 B:0個 → A:1個 B:0個 → A:2個 B:0個 → A:2個 B:2個
(1)4回目の操作を終えたとき、袋Aの中に3個以上の玉が入っている確率は$\boxed{\ \ カ\ \ }$である。また、4回目の操作を終えた時点で袋Aの中に3個以上の玉が入っているという条件の下で、7回目の操作を終えたとき袋Bの中に入っている玉の数が3個以下である条件付き確率は$\boxed{\ \ キ\ \ }$である。
(2)$n$回目の操作を終えたとき、袋Aの中に入っている玉の数のほうが、袋Bの中に入っている玉の数より多い確率を$p_n$とする。
$p_{n+1}$を$p_n$を用いて表すと$p_{n+1}$=$\boxed{\ \ ク\ \ }$となり、これより$p_n$を$n$を用いて表すと$p_n$=$\boxed{\ \ ケ\ \ }$となる。
(3)$n$回目($n$≧4)の操作を終えたとき、袋Aの中に$n-1$個以上の玉が入っている確率は$\boxed{\ \ コ\ \ }$であり、$n-2$個以上の玉が入っている確率は$\boxed{\ \ サ\ \ }$である。
この動画を見る
$\Large\boxed{3}$ 何も入っていない2つの袋A,Bがある。いま、「硬貨を1枚投げて表が出たら袋A、裏が出たら袋Bを選び、以下のルールに従って選んだ袋の中に玉を入れる」
という操作を繰り返す。
ルール
・選んだ袋の中に入っている玉の数がもう一方の袋の中に入っている玉の数より多いか、2つの袋の中に入っている玉の数が同じとき、選んだ袋の中に玉を1個入れる。
・選んだ袋の中に入っている玉の数がもう一方の袋の中に入っている玉の数より少ないとき、選んだ袋の中に入っている玉の数が、もう一方の袋の中に入っている玉の数と同じになるまで選んだ袋の中に玉をいれる。
たとえば、上の操作を3回行ったとき、硬貨が順に表、表、裏と出たとすると、
A,B2つの袋の中の玉の数は次のように変化する。
A:0個 B:0個 → A:1個 B:0個 → A:2個 B:0個 → A:2個 B:2個
(1)4回目の操作を終えたとき、袋Aの中に3個以上の玉が入っている確率は$\boxed{\ \ カ\ \ }$である。また、4回目の操作を終えた時点で袋Aの中に3個以上の玉が入っているという条件の下で、7回目の操作を終えたとき袋Bの中に入っている玉の数が3個以下である条件付き確率は$\boxed{\ \ キ\ \ }$である。
(2)$n$回目の操作を終えたとき、袋Aの中に入っている玉の数のほうが、袋Bの中に入っている玉の数より多い確率を$p_n$とする。
$p_{n+1}$を$p_n$を用いて表すと$p_{n+1}$=$\boxed{\ \ ク\ \ }$となり、これより$p_n$を$n$を用いて表すと$p_n$=$\boxed{\ \ ケ\ \ }$となる。
(3)$n$回目($n$≧4)の操作を終えたとき、袋Aの中に$n-1$個以上の玉が入っている確率は$\boxed{\ \ コ\ \ }$であり、$n-2$個以上の玉が入っている確率は$\boxed{\ \ サ\ \ }$である。
福田の数学〜慶應義塾大学2023年理工学部第3問〜確率と漸化式(難問)Part2

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 何も入っていない2つの袋A,Bがある。いま、「硬貨を1枚投げて表が出たら袋A、裏が出たら袋Bを選び、以下のルールに従って選んだ袋の中に玉を入れる」
という操作を繰り返す。
ルール
・選んだ袋の中に入っている玉の数がもう一方の袋の中に入っている玉の数より多いか、2つの袋の中に入っている玉の数が同じとき、選んだ袋の中に玉を1個入れる。
・選んだ袋の中に入っている玉の数がもう一方の袋の中に入っている玉の数より少ないとき、選んだ袋の中に入っている玉の数が、もう一方の袋の中に入っている玉の数と同じになるまで選んだ袋の中に玉をいれる。
たとえば、上の操作を3回行ったとき、硬貨が順に表、表、裏と出たとすると、
A,B2つの袋の中の玉の数は次のように変化する。
A:0個 B:0個 → A:1個 B:0個 → A:2個 B:0個 → A:2個 B:2個
(1)4回目の操作を終えたとき、袋Aの中に3個以上の玉が入っている確率は$\boxed{\ \ カ\ \ }$である。また、4回目の操作を終えた時点で袋Aの中に3個以上の玉が入っているという条件の下で、7回目の操作を終えたとき袋Bの中に入っている玉の数が3個以下である条件付き確率は$\boxed{\ \ キ\ \ }$である。
(2)$n$回目の操作を終えたとき、袋Aの中に入っている玉の数のほうが、袋Bの中に入っている玉の数より多い確率を$p_n$とする。
$p_{n+1}$を$p_n$を用いて表すと$p_{n+1}$=$\boxed{\ \ ク\ \ }$となり、これより$p_n$を$n$を用いて表すと$p_n$=$\boxed{\ \ ケ\ \ }$となる。
(3)$n$回目($n$≧4)の操作を終えたとき、袋Aの中に$n-1$個以上の玉が入っている確率は$\boxed{\ \ コ\ \ }$であり、$n-2$個以上の玉が入っている確率は$\boxed{\ \ サ\ \ }$である。
この動画を見る
$\Large\boxed{3}$ 何も入っていない2つの袋A,Bがある。いま、「硬貨を1枚投げて表が出たら袋A、裏が出たら袋Bを選び、以下のルールに従って選んだ袋の中に玉を入れる」
という操作を繰り返す。
ルール
・選んだ袋の中に入っている玉の数がもう一方の袋の中に入っている玉の数より多いか、2つの袋の中に入っている玉の数が同じとき、選んだ袋の中に玉を1個入れる。
・選んだ袋の中に入っている玉の数がもう一方の袋の中に入っている玉の数より少ないとき、選んだ袋の中に入っている玉の数が、もう一方の袋の中に入っている玉の数と同じになるまで選んだ袋の中に玉をいれる。
たとえば、上の操作を3回行ったとき、硬貨が順に表、表、裏と出たとすると、
A,B2つの袋の中の玉の数は次のように変化する。
A:0個 B:0個 → A:1個 B:0個 → A:2個 B:0個 → A:2個 B:2個
(1)4回目の操作を終えたとき、袋Aの中に3個以上の玉が入っている確率は$\boxed{\ \ カ\ \ }$である。また、4回目の操作を終えた時点で袋Aの中に3個以上の玉が入っているという条件の下で、7回目の操作を終えたとき袋Bの中に入っている玉の数が3個以下である条件付き確率は$\boxed{\ \ キ\ \ }$である。
(2)$n$回目の操作を終えたとき、袋Aの中に入っている玉の数のほうが、袋Bの中に入っている玉の数より多い確率を$p_n$とする。
$p_{n+1}$を$p_n$を用いて表すと$p_{n+1}$=$\boxed{\ \ ク\ \ }$となり、これより$p_n$を$n$を用いて表すと$p_n$=$\boxed{\ \ ケ\ \ }$となる。
(3)$n$回目($n$≧4)の操作を終えたとき、袋Aの中に$n-1$個以上の玉が入っている確率は$\boxed{\ \ コ\ \ }$であり、$n-2$個以上の玉が入っている確率は$\boxed{\ \ サ\ \ }$である。
福田の数学〜慶應義塾大学2023年理工学部第3問〜確率と漸化式(難問)Part1

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 何も入っていない2つの袋A,Bがある。いま、「硬貨を1枚投げて表が出たら袋A、裏が出たら袋Bを選び、以下のルールに従って選んだ袋の中に玉を入れる」
という操作を繰り返す。
ルール
・選んだ袋の中に入っている玉の数がもう一方の袋の中に入っている玉の数より多いか、2つの袋の中に入っている玉の数が同じとき、選んだ袋の中に玉を1個入れる。
・選んだ袋の中に入っている玉の数がもう一方の袋の中に入っている玉の数より少ないとき、選んだ袋の中に入っている玉の数が、もう一方の袋の中に入っている玉の数と同じになるまで選んだ袋の中に玉をいれる。
たとえば、上の操作を3回行ったとき、硬貨が順に表、表、裏と出たとすると、
A,B2つの袋の中の玉の数は次のように変化する。
A:0個 B:0個 → A:1個 B:0個 → A:2個 B:0個 → A:2個 B:2個
(1)4回目の操作を終えたとき、袋Aの中に3個以上の玉が入っている確率は$\boxed{\ \ カ\ \ }$である。また、4回目の操作を終えた時点で袋Aの中に3個以上の玉が入っているという条件の下で、7回目の操作を終えたとき袋Bの中に入っている玉の数が3個以下である条件付き確率は$\boxed{\ \ キ\ \ }$である。
(2)$n$回目の操作を終えたとき、袋Aの中に入っている玉の数のほうが、袋Bの中に入っている玉の数より多い確率を$p_n$とする。
$p_{n+1}$を$p_n$を用いて表すと$p_{n+1}$=$\boxed{\ \ ク\ \ }$となり、これより$p_n$を$n$を用いて表すと$p_n$=$\boxed{\ \ ケ\ \ }$となる。
(3)$n$回目($n$≧4)の操作を終えたとき、袋Aの中に$n-1$個以上の玉が入っている確率は$\boxed{\ \ コ\ \ }$であり、$n-2$個以上の玉が入っている確率は$\boxed{\ \ サ\ \ }$である。
この動画を見る
$\Large\boxed{3}$ 何も入っていない2つの袋A,Bがある。いま、「硬貨を1枚投げて表が出たら袋A、裏が出たら袋Bを選び、以下のルールに従って選んだ袋の中に玉を入れる」
という操作を繰り返す。
ルール
・選んだ袋の中に入っている玉の数がもう一方の袋の中に入っている玉の数より多いか、2つの袋の中に入っている玉の数が同じとき、選んだ袋の中に玉を1個入れる。
・選んだ袋の中に入っている玉の数がもう一方の袋の中に入っている玉の数より少ないとき、選んだ袋の中に入っている玉の数が、もう一方の袋の中に入っている玉の数と同じになるまで選んだ袋の中に玉をいれる。
たとえば、上の操作を3回行ったとき、硬貨が順に表、表、裏と出たとすると、
A,B2つの袋の中の玉の数は次のように変化する。
A:0個 B:0個 → A:1個 B:0個 → A:2個 B:0個 → A:2個 B:2個
(1)4回目の操作を終えたとき、袋Aの中に3個以上の玉が入っている確率は$\boxed{\ \ カ\ \ }$である。また、4回目の操作を終えた時点で袋Aの中に3個以上の玉が入っているという条件の下で、7回目の操作を終えたとき袋Bの中に入っている玉の数が3個以下である条件付き確率は$\boxed{\ \ キ\ \ }$である。
(2)$n$回目の操作を終えたとき、袋Aの中に入っている玉の数のほうが、袋Bの中に入っている玉の数より多い確率を$p_n$とする。
$p_{n+1}$を$p_n$を用いて表すと$p_{n+1}$=$\boxed{\ \ ク\ \ }$となり、これより$p_n$を$n$を用いて表すと$p_n$=$\boxed{\ \ ケ\ \ }$となる。
(3)$n$回目($n$≧4)の操作を終えたとき、袋Aの中に$n-1$個以上の玉が入っている確率は$\boxed{\ \ コ\ \ }$であり、$n-2$個以上の玉が入っている確率は$\boxed{\ \ サ\ \ }$である。
福田の数学〜慶應義塾大学2023年理工学部第2問〜空間ベクトルと2直線から等距離にある点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#図形と方程式#軌跡と領域#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ $k$を正の実数とし、空間内に点O(0,0,0), A(4$k$, $-4k$, $-4\sqrt 2k$), B(7, 5, $-\sqrt 2$)をとる。点CはO, A, Bを含む平面上の点であり、OA=4BCで、四角形OACBはOAを底辺とする台形であるとする。
(1)$\cos\angle$AOB=$\boxed{\ \ ア\ \ }$である。台形OACBの面積を$k$を用いて表すと$\boxed{\ \ イ\ \ }$となる。
また、線分ACの長さを$k$を用いて表すと$\boxed{\ \ ウ\ \ }$となる。
(2)台形OACBが円に内接するとき、$k$=$\boxed{\ \ エ\ \ }$である。
(3)$k$=$\boxed{\ \ エ\ \ }$であるとし、直線OBと直線ACの交点をDとする。△OBPと△ACPの面積が等しい、という条件を満たす空間内の点P全体は、点Dを通る2つの平面上の点全体から点Dを除いたものとなる。これら2つの平面のうち、線分OAと交わらないものを$\alpha$とする。点Oから平面$\alpha$に下ろした垂線の長さは$\boxed{\ \ オ\ \ }$である。
この動画を見る
$\Large\boxed{2}$ $k$を正の実数とし、空間内に点O(0,0,0), A(4$k$, $-4k$, $-4\sqrt 2k$), B(7, 5, $-\sqrt 2$)をとる。点CはO, A, Bを含む平面上の点であり、OA=4BCで、四角形OACBはOAを底辺とする台形であるとする。
(1)$\cos\angle$AOB=$\boxed{\ \ ア\ \ }$である。台形OACBの面積を$k$を用いて表すと$\boxed{\ \ イ\ \ }$となる。
また、線分ACの長さを$k$を用いて表すと$\boxed{\ \ ウ\ \ }$となる。
(2)台形OACBが円に内接するとき、$k$=$\boxed{\ \ エ\ \ }$である。
(3)$k$=$\boxed{\ \ エ\ \ }$であるとし、直線OBと直線ACの交点をDとする。△OBPと△ACPの面積が等しい、という条件を満たす空間内の点P全体は、点Dを通る2つの平面上の点全体から点Dを除いたものとなる。これら2つの平面のうち、線分OAと交わらないものを$\alpha$とする。点Oから平面$\alpha$に下ろした垂線の長さは$\boxed{\ \ オ\ \ }$である。
福田の数学〜慶應義塾大学2023年理工学部第1問(3)〜関数の増減と平均値の定理

単元:
#大学入試過去問(数学)#微分とその応用#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)閉区間[0,1]上で定義された連続関数$h(x)$が、開区間(0,1)で微分可能であり、この区間で常に$h'(x)$<0であるとする。このとき、$h(x)$が区間[0,1]で減少することを、平均値の定理を用いて証明しなさい。
この動画を見る
$\Large\boxed{1}$ (3)閉区間[0,1]上で定義された連続関数$h(x)$が、開区間(0,1)で微分可能であり、この区間で常に$h'(x)$<0であるとする。このとき、$h(x)$が区間[0,1]で減少することを、平均値の定理を用いて証明しなさい。
福田の数学〜慶應義塾大学2023年理工学部第1問(2)〜微分可能性

単元:
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)$g(x)$=$|x|\sqrt{x^2+1}$とする。$g(x)$が$x$=0で微分可能でないことを証明しなさい。
この動画を見る
$\Large\boxed{1}$ (2)$g(x)$=$|x|\sqrt{x^2+1}$とする。$g(x)$が$x$=0で微分可能でないことを証明しなさい。
福田の数学〜慶應義塾大学2023年理工学部第1問(1)〜微分係数の定義

単元:
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)$f(x)$=$x^4$とする。$f(x)$の$x$=$a$における微分係数を、定義に従って求めなさい。
次の関数に関しても$x$=$a$における微分係数を、定義に従って求めなさい。
$g(x)$=$\sin x$
$h(x)$=$\log x$
この動画を見る
$\Large\boxed{1}$ (1)$f(x)$=$x^4$とする。$f(x)$の$x$=$a$における微分係数を、定義に従って求めなさい。
次の関数に関しても$x$=$a$における微分係数を、定義に従って求めなさい。
$g(x)$=$\sin x$
$h(x)$=$\log x$
大学入試問題#613「微分してたら、時間かかるだろうな~~」 慶應義塾大学(1996)

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \frac{10x-x^2}{(10+10x-x^2)^2}$の最大値を求めよ
出典:1996年慶應義塾大学 入試問題
この動画を見る
$\displaystyle \frac{10x-x^2}{(10+10x-x^2)^2}$の最大値を求めよ
出典:1996年慶應義塾大学 入試問題
大学入試問題#612「チャートにありそう」 慶応義塾大学(2011) #2次不等式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
すべての実数$y$に対して$x^2+xy+y^2 \gt x+y$が成り立つ$x$の値の範囲を求めよ。
出典:2011年慶應義塾大学 入試問題
この動画を見る
すべての実数$y$に対して$x^2+xy+y^2 \gt x+y$が成り立つ$x$の値の範囲を求めよ。
出典:2011年慶應義塾大学 入試問題
慶應義塾大(経済)数列の最大値

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#慶應義塾大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
2011慶應義塾大学過去問題
n=1,2,・・・100
$a_n=n3^n$・${}_{100} \mathrm{ C }_n$
$a_n$を最大にするnの値
この動画を見る
2011慶應義塾大学過去問題
n=1,2,・・・100
$a_n=n3^n$・${}_{100} \mathrm{ C }_n$
$a_n$を最大にするnの値
慶應義塾大 直線の傾き

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2016慶応義塾大学過去問題
aは整数、aの値は?
$f(x)=x^3-x^2-x+c$
$A(0,f(x)),B(a,f(a))$
直線ABと$x=\frac{a}{3}$におけるf(x)の接線が直交する。
この動画を見る
2016慶応義塾大学過去問題
aは整数、aの値は?
$f(x)=x^3-x^2-x+c$
$A(0,f(x)),B(a,f(a))$
直線ABと$x=\frac{a}{3}$におけるf(x)の接線が直交する。
慶應大 簡単すぎたので1問付け加えてみた

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023慶応義塾大学過去問題
$P(x)=\displaystyle\sum_{n=1}^{20}nx^n=20x^{20}+19x^{19}+$
$\cdots+2x^2+x$
を①$x-1$,②$x^2-1$で割った余り
おまけ
$x^3-1$で割った余り
この動画を見る
2023慶応義塾大学過去問題
$P(x)=\displaystyle\sum_{n=1}^{20}nx^n=20x^{20}+19x^{19}+$
$\cdots+2x^2+x$
を①$x-1$,②$x^2-1$で割った余り
おまけ
$x^3-1$で割った余り
微分の定義!慶應義塾大

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#慶應義塾大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023慶応義塾大学過去問題
$f(x)=x^4$とする
f(x)のx=aにおける微分係数を定義に従って求めなさい
計算過程も記述しなさい
この動画を見る
2023慶応義塾大学過去問題
$f(x)=x^4$とする
f(x)のx=aにおける微分係数を定義に従って求めなさい
計算過程も記述しなさい
福田の数学〜慶應義塾大学2023年看護医療学部第5問〜散布図と箱ひげ図の関係と相関係数
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#データの分析#データの分析#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
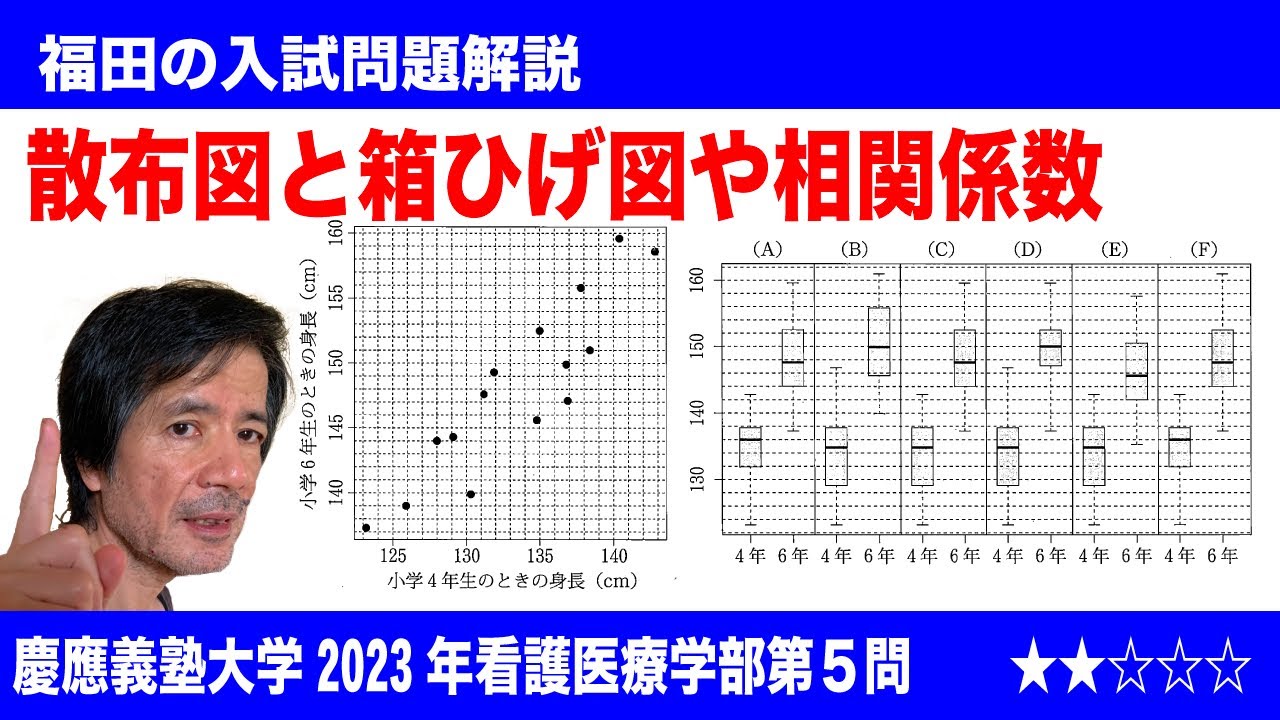
$\Large\boxed{5}$ 以下の図は、ある小学校の15人の女子児童の4年生の4月に計測した身長を横軸に、5年生の4月に計測した身長を縦軸にとった散布図である。(※動画参照)
と表すことができる。よってS(a)を最小にするaはa=$\boxed{\ \ ミ\ \ }$である。
S(a)の最小値は、女子児童の4年生のときと6年生のときの身長の相関係数rと$s_y^2$を用いて$\boxed{\ \ ム\ \ }$と表せる。
また、左の散布図で示した女子児童の計測値を計算すると
$s_x^2$=29.00, $s_y^2$=42.65, $s_{xy}$=31.69
であった。これらを用いてS(a)を最小にするaを計算し、小数第4位を四捨五入すると$\boxed{\ \ メ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{5}$ 以下の図は、ある小学校の15人の女子児童の4年生の4月に計測した身長を横軸に、5年生の4月に計測した身長を縦軸にとった散布図である。(※動画参照)
と表すことができる。よってS(a)を最小にするaはa=$\boxed{\ \ ミ\ \ }$である。
S(a)の最小値は、女子児童の4年生のときと6年生のときの身長の相関係数rと$s_y^2$を用いて$\boxed{\ \ ム\ \ }$と表せる。
また、左の散布図で示した女子児童の計測値を計算すると
$s_x^2$=29.00, $s_y^2$=42.65, $s_{xy}$=31.69
であった。これらを用いてS(a)を最小にするaを計算し、小数第4位を四捨五入すると$\boxed{\ \ メ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
