 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
#千葉大学2021#不定積分#元高専教員
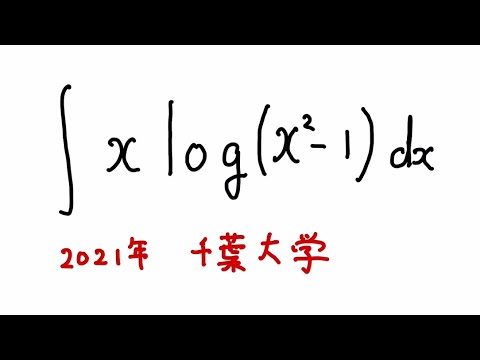
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け。
$\displaystyle \int x log(x^2-1) dx$
出典:2021年千葉大学
この動画を見る
以下の不定積分を解け。
$\displaystyle \int x log(x^2-1) dx$
出典:2021年千葉大学
積分区間は0→π/4です。大学入試問題#900「減点ポイント多い問題」 #横浜国立大学後期(2023)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#横浜国立大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$n$を正の整数とする。
関数$F(x)=\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{2e^x\cos t\sin t}{(\cos^2t+x^n\sin^2t)^2} dt$
について、次の問いに答えよ。
ただし、$x \gt 0$とする。
1.$F(x)$を求めよ。
2.$F(x)$が極値をもつ最小の$n$の値を求めよ。
出典:2023年横浜国立大学後期
この動画を見る
$n$を正の整数とする。
関数$F(x)=\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{2e^x\cos t\sin t}{(\cos^2t+x^n\sin^2t)^2} dt$
について、次の問いに答えよ。
ただし、$x \gt 0$とする。
1.$F(x)$を求めよ。
2.$F(x)$が極値をもつ最小の$n$の値を求めよ。
出典:2023年横浜国立大学後期
#千葉大学2018#不定積分#数学者
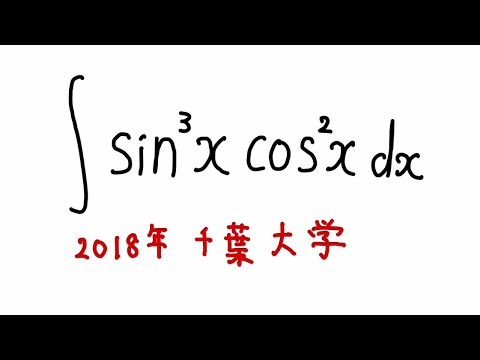
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け。
$\displaystyle \int \sin^3x \cos^2x$ $dx$
出典:2018年千葉大学
この動画を見る
以下の不定積分を解け。
$\displaystyle \int \sin^3x \cos^2x$ $dx$
出典:2018年千葉大学
大学入試問題#899「初めてのベクトルやってみた」 #北海道大学(2024)

単元:
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数C
指導講師:
ますただ
問題文全文(内容文):
三角形$OAB$が
$|\overrightarrow{ OA }|=3,$ $|\overrightarrow{ AB }|=5,$ $\overrightarrow{ OA }.\overrightarrow{ AB }=10$
を満たしているとする。
三角形$OAB$の内接円の中心を$I$とし、この内接円と辺$OA$の接点を$H$とする。
1.辺$OB$の長さを求めよ。
2.$\overrightarrow{ OI }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$を用いて表せ。
3.$\overrightarrow{ HI }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$を用いて表せ。
出典:2024年北海道大学
この動画を見る
三角形$OAB$が
$|\overrightarrow{ OA }|=3,$ $|\overrightarrow{ AB }|=5,$ $\overrightarrow{ OA }.\overrightarrow{ AB }=10$
を満たしているとする。
三角形$OAB$の内接円の中心を$I$とし、この内接円と辺$OA$の接点を$H$とする。
1.辺$OB$の長さを求めよ。
2.$\overrightarrow{ OI }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$を用いて表せ。
3.$\overrightarrow{ HI }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$を用いて表せ。
出典:2024年北海道大学
福田の数学〜中央大学2024経済学部第1問(4)〜タンジェントの加法定理

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
・ $\tan\alpha=2,\tan\beta=3$のとき$\alpha+\beta$を求めよ。ただし、$0 < \alpha < \dfrac\pi2,0 < \beta < \dfrac\pi2$とする。
・ $\tan\alpha=2,\tan\beta=5,\tan\gamma=8$のとき$\alpha+\beta+\gamma$を求めよ。ただし、$\alpha,\beta,\gamma$は鋭角とする。
この動画を見る
・ $\tan\alpha=2,\tan\beta=3$のとき$\alpha+\beta$を求めよ。ただし、$0 < \alpha < \dfrac\pi2,0 < \beta < \dfrac\pi2$とする。
・ $\tan\alpha=2,\tan\beta=5,\tan\gamma=8$のとき$\alpha+\beta+\gamma$を求めよ。ただし、$\alpha,\beta,\gamma$は鋭角とする。
#千葉大学2022#極限#ますただ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } (\sqrt{ n^2+n }-n)$
出典:2022年千葉大学
この動画を見る
$\displaystyle \lim_{ n \to \infty } (\sqrt{ n^2+n }-n)$
出典:2022年千葉大学
大学入試問題#898「教科書例題」 #千葉大学(2024)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
次の等式を満たす$x \gt 0$で定義された関数$f(x)$と定数$a$の値を求めよ。
ただし、$a \gt 0$とする。
$\displaystyle \int_{a}^{x} f(t) dt=x+\displaystyle \frac{1}{2}log$ $x-1$
出典:2024年千葉大学
この動画を見る
次の等式を満たす$x \gt 0$で定義された関数$f(x)$と定数$a$の値を求めよ。
ただし、$a \gt 0$とする。
$\displaystyle \int_{a}^{x} f(t) dt=x+\displaystyle \frac{1}{2}log$ $x-1$
出典:2024年千葉大学
福田の数学〜中央大学2024経済学部第1問(3)〜パスワードで無事にログインできる確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
あるWebサイトにログインするには4桁の暗証番号を入力しなければならないが、それを忘れてしまった。覚えているのは、各桁の数は5以上ですべて異なる数であり、末尾の2桁は$78$か$87$のどちらかということだけである。このWebサイトでは暗証番号は3回まで入力することができるが、記憶に当てはまる班員台で手当たり次第に入力して無事にログインできる確率を求めよ。
この動画を見る
あるWebサイトにログインするには4桁の暗証番号を入力しなければならないが、それを忘れてしまった。覚えているのは、各桁の数は5以上ですべて異なる数であり、末尾の2桁は$78$か$87$のどちらかということだけである。このWebサイトでは暗証番号は3回まで入力することができるが、記憶に当てはまる班員台で手当たり次第に入力して無事にログインできる確率を求めよ。
#千葉大学2020#不定積分#ますただ
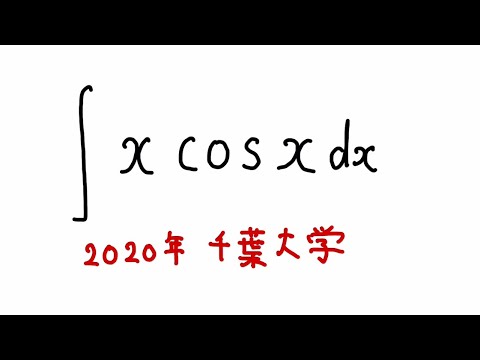
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int x\cos x$ $dx$
出典:2024年千葉大学
この動画を見る
$\displaystyle \int x\cos x$ $dx$
出典:2024年千葉大学
大学入試問題#897「解法の迷走」 #北海道大学(2024)

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \frac{x^2-x+1}{x^2+x+1}$
が整数となるような実数$x$をすべて求めよ。
出典:2024年北海道大学後期
この動画を見る
$\displaystyle \frac{x^2-x+1}{x^2+x+1}$
が整数となるような実数$x$をすべて求めよ。
出典:2024年北海道大学後期
福田の数学〜中央大学2024経済学部第1問(2)〜集合の要素の個数

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$1$から$1000$までの整数全体の集合を$U$とする。$U$の部分集合$A,B$をそれぞれ$A=\{x|xは5の倍数\},B=\{x|xは7の倍数\}$とするとき、$\overline A \cap \overline B$の要素の個数$n(\overline A \cap \overline B)$を求めよ。
この動画を見る
$1$から$1000$までの整数全体の集合を$U$とする。$U$の部分集合$A,B$をそれぞれ$A=\{x|xは5の倍数\},B=\{x|xは7の倍数\}$とするとき、$\overline A \cap \overline B$の要素の個数$n(\overline A \cap \overline B)$を求めよ。
大学入試問題#896「難関大学ではたまにでる?」 #北海道大学(2024)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
ますただ
問題文全文(内容文):
関数$f_1(x),f_2(x),f_3(x),…$を次の関係式で定める。
$f_1(x)=3x$
$f_{n+1}(x)=(n+2)x^{n+1}+(\displaystyle \int_{0}^{1} f_n(t) dt)x$
関数$f_n(x)$を$x$と$n$の式で表せ。$(n=1,2,3,…)$
出典:2024年北海道大学
この動画を見る
関数$f_1(x),f_2(x),f_3(x),…$を次の関係式で定める。
$f_1(x)=3x$
$f_{n+1}(x)=(n+2)x^{n+1}+(\displaystyle \int_{0}^{1} f_n(t) dt)x$
関数$f_n(x)$を$x$と$n$の式で表せ。$(n=1,2,3,…)$
出典:2024年北海道大学
大学入試問題#895「2番だけで良い大問」 #福井大学医学部(2015) #数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#福井大学#数B
指導講師:
ますただ
問題文全文(内容文):
$a_1=2$
$3a_{n+1}-4a_n+1=0$
1.数列{$a_n$}の一般項を求めよ。
2.$\displaystyle \frac{a_{n+1}}{a_n}$の小数部分を$b_n$とし、数列{$b_n$}の一般項を求めよ。
3.$\displaystyle \sum_{k=1}^n \displaystyle \frac{1}{b_k}$を求めよ。
出典:2015年福井大学医学部
この動画を見る
$a_1=2$
$3a_{n+1}-4a_n+1=0$
1.数列{$a_n$}の一般項を求めよ。
2.$\displaystyle \frac{a_{n+1}}{a_n}$の小数部分を$b_n$とし、数列{$b_n$}の一般項を求めよ。
3.$\displaystyle \sum_{k=1}^n \displaystyle \frac{1}{b_k}$を求めよ。
出典:2015年福井大学医学部
#千葉大学2024#定積分
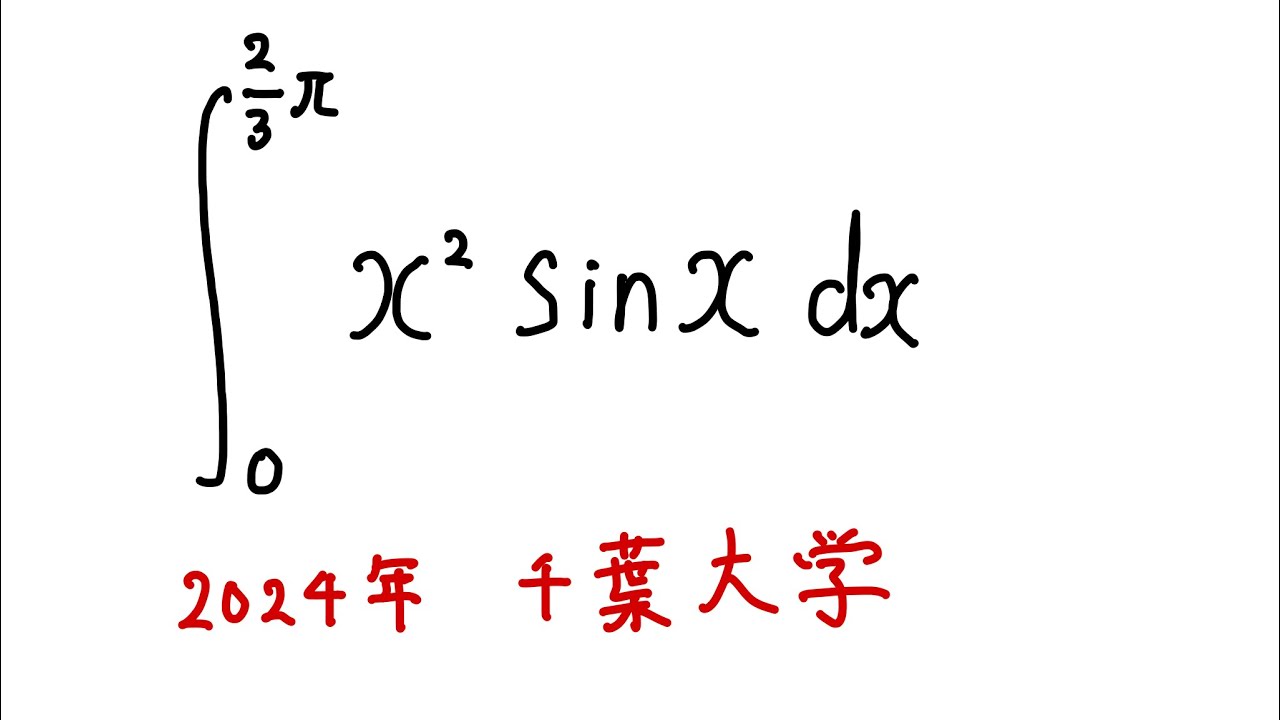
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{2}{3}\pi} x^2\sin x$ $dx$
出典:2024年千葉大学
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{2}{3}\pi} x^2\sin x$ $dx$
出典:2024年千葉大学
#千葉大学2023#定積分#ますただ
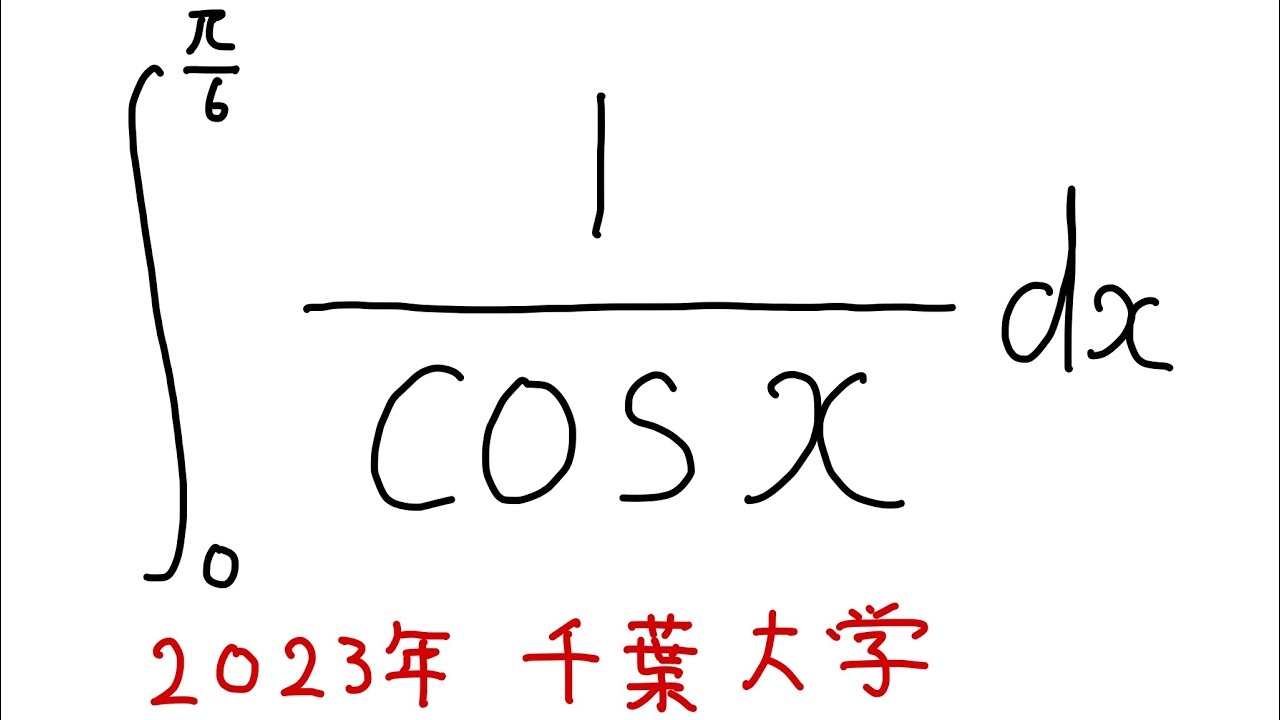
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{1}{\cos x} dx$
出典:2023年千葉大学
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{1}{\cos x} dx$
出典:2023年千葉大学
#千葉大学2023#定積分
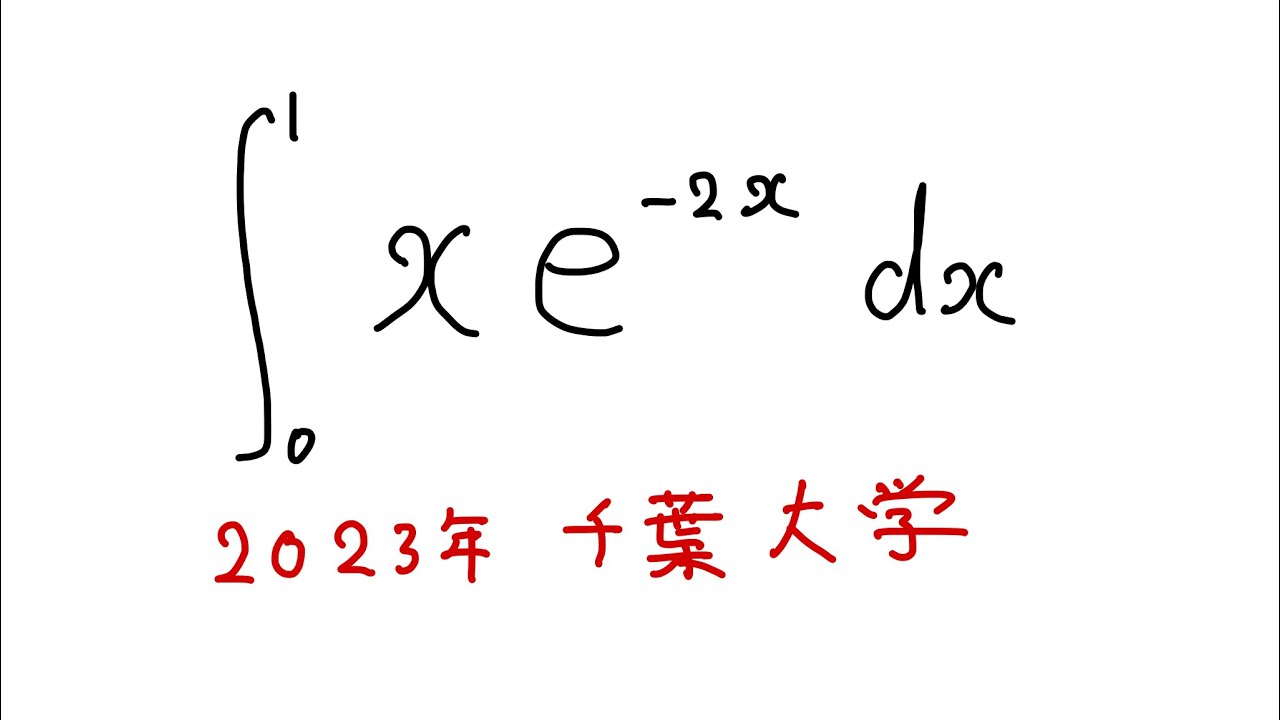
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
下記の定積分を解け
$\displaystyle \int_{0}^{1} xe^{-2x} dx$
出典:2023年千葉大学
この動画を見る
下記の定積分を解け
$\displaystyle \int_{0}^{1} xe^{-2x} dx$
出典:2023年千葉大学
#広島市立大学#不定積分#ますただ
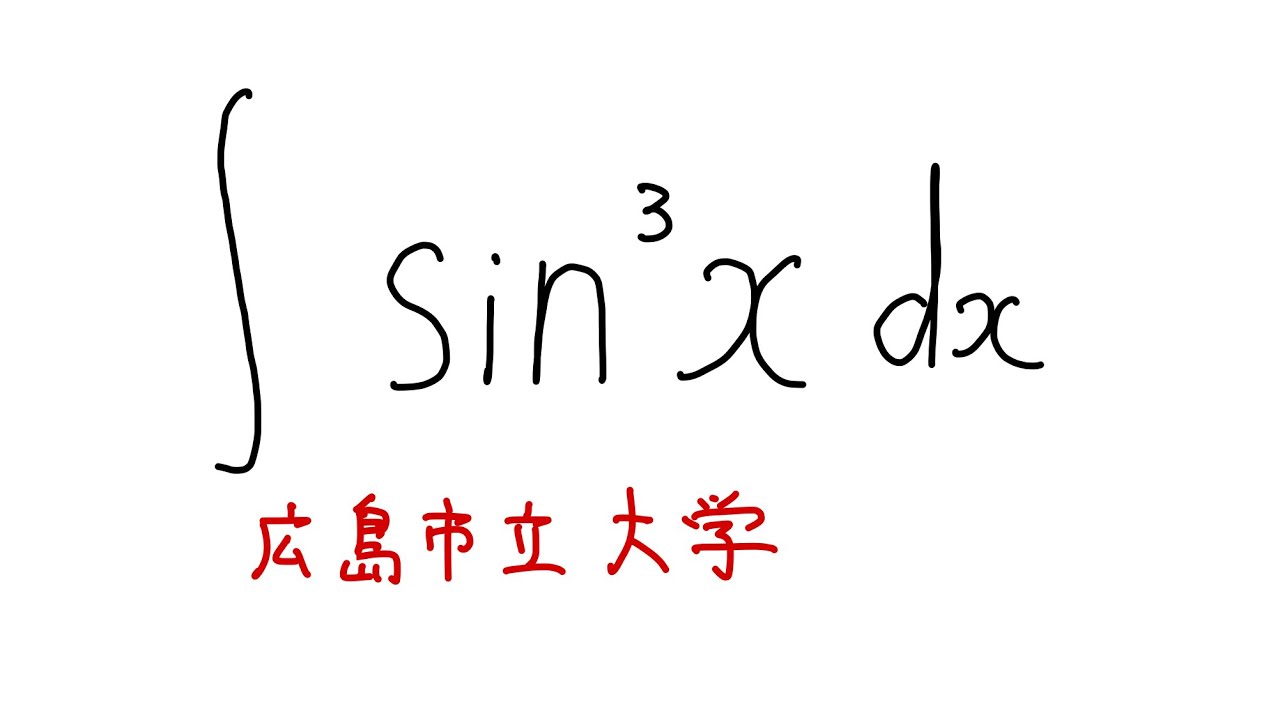
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \sin^3 x$ $dx$
広島市立大過去問
この動画を見る
$\displaystyle \int \sin^3 x$ $dx$
広島市立大過去問
大学入試問題#893「難易度クソ高め」 #信州大学(2015)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \int_{2}^{x} \displaystyle \frac{t^2}{(t^2-1)^2}dt$
出典:2015年信州大学後期
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \int_{2}^{x} \displaystyle \frac{t^2}{(t^2-1)^2}dt$
出典:2015年信州大学後期
福田の数学〜筑波大学2024理系第4問〜媒介変数表示で表された曲線のグラフと面積

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標平面において、媒介変数表示$x=-t(t-\dfrac32), y=\sin\pi t ~~ (0\leqq t \leqq 1)$で表される曲線を$C$とする。以下の問いに答えよ
(1) 定積分$\displaystyle \int_0^1 t\sin\pi t dt$を求めよ。
(2) 実数$a$に対し、曲線$C$と直線$x=a$の共有点の個数を求めよ。
(3) 曲線$C$と$x$軸で囲まれた図形の面積を求めよ。
この動画を見る
座標平面において、媒介変数表示$x=-t(t-\dfrac32), y=\sin\pi t ~~ (0\leqq t \leqq 1)$で表される曲線を$C$とする。以下の問いに答えよ
(1) 定積分$\displaystyle \int_0^1 t\sin\pi t dt$を求めよ。
(2) 実数$a$に対し、曲線$C$と直線$x=a$の共有点の個数を求めよ。
(3) 曲線$C$と$x$軸で囲まれた図形の面積を求めよ。
#電気通信大学2015#区分求積法#ますただ
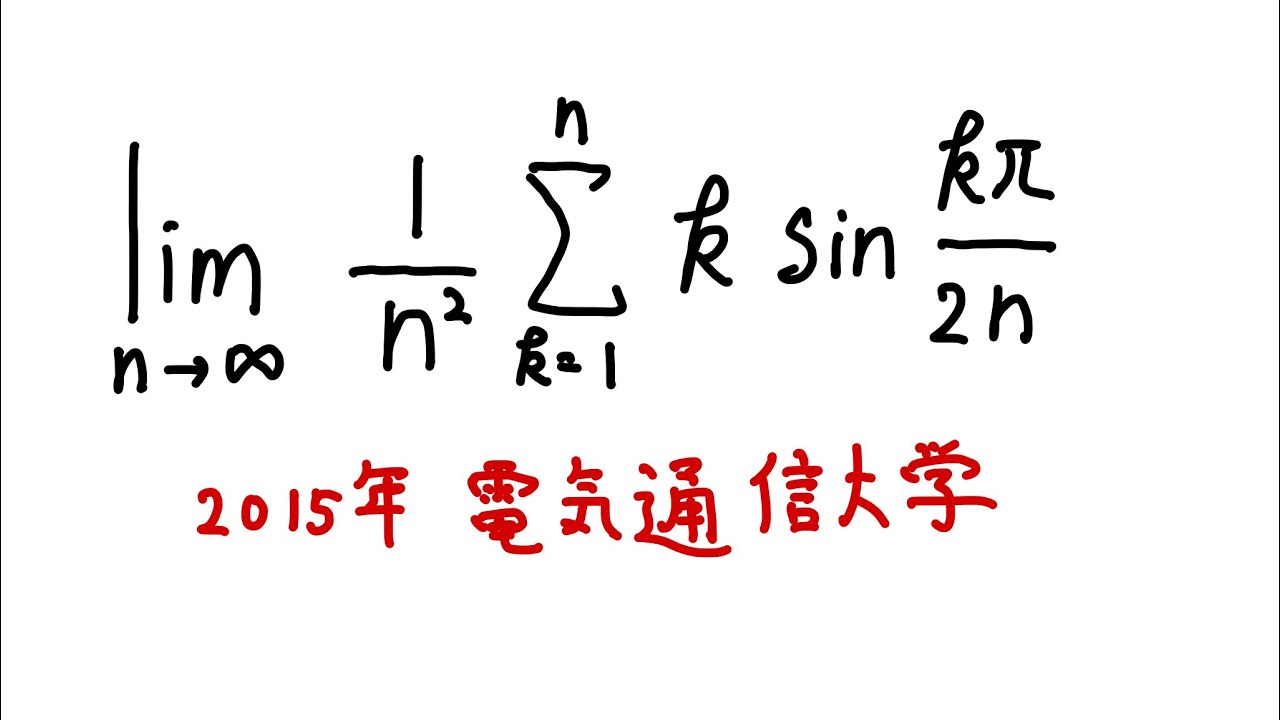
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n^2}\displaystyle \sum_{k=1}^n k \sin\displaystyle \frac{k\pi}{2n}$
出典:2015年電気通信大学
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n^2}\displaystyle \sum_{k=1}^n k \sin\displaystyle \frac{k\pi}{2n}$
出典:2015年電気通信大学
#富山大学推薦2019#定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#富山大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{\sqrt{ 3 }} \displaystyle \frac{x}{x^2+1} dx$
出典:2019年富山大学推薦
この動画を見る
$\displaystyle \int_{1}^{\sqrt{ 3 }} \displaystyle \frac{x}{x^2+1} dx$
出典:2019年富山大学推薦
大学入試問題#892「数学はやっぱ根性」 #京都工芸繊維大学(2023)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$0 \leq \theta \leq \displaystyle \frac{\pi}{4}$とする
$f(\theta)=\displaystyle \int_{0}^{\frac{\pi}{4}} \displaystyle \frac{|\sin\theta-\sin x|}{\cos^2x} dx$
出典:2023年京都工芸繊維大学
この動画を見る
$0 \leq \theta \leq \displaystyle \frac{\pi}{4}$とする
$f(\theta)=\displaystyle \int_{0}^{\frac{\pi}{4}} \displaystyle \frac{|\sin\theta-\sin x|}{\cos^2x} dx$
出典:2023年京都工芸繊維大学
福田の数学〜筑波大学2024理系第3問〜3次関数のグラフと接線

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=x(x+1)(x-1)$とする。座標平面において、曲線$y=f(x)$を$C$とし、曲線$C$上の点$(t,f(t))$における接線を$L$とする。以下の問いに答えよ。
(1) 直線$L$の方程式を$t$を用いて表せ。
(2) $t \neq 0$のとき、直線$L$と曲線$C$の共有点で、点$(t,f(t))$とは異なるものを$(a,f(a))$とする。$a$を$t$を用いて表せ。また$t$が$0$を除いた実数を動くとき、$f'(t)f'(a)$の最小値を求めよ。
(3) 次の条件Aを満たすような実数$t$の範囲を求めよ。
(A) 曲線$C$上の点$(t,f(t))$における接線が直線$L$と直交するような実数$s$が存在する。
この動画を見る
$f(x)=x(x+1)(x-1)$とする。座標平面において、曲線$y=f(x)$を$C$とし、曲線$C$上の点$(t,f(t))$における接線を$L$とする。以下の問いに答えよ。
(1) 直線$L$の方程式を$t$を用いて表せ。
(2) $t \neq 0$のとき、直線$L$と曲線$C$の共有点で、点$(t,f(t))$とは異なるものを$(a,f(a))$とする。$a$を$t$を用いて表せ。また$t$が$0$を除いた実数を動くとき、$f'(t)f'(a)$の最小値を求めよ。
(3) 次の条件Aを満たすような実数$t$の範囲を求めよ。
(A) 曲線$C$上の点$(t,f(t))$における接線が直線$L$と直交するような実数$s$が存在する。
#広島市立大学2014#不定積分#ますただ
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
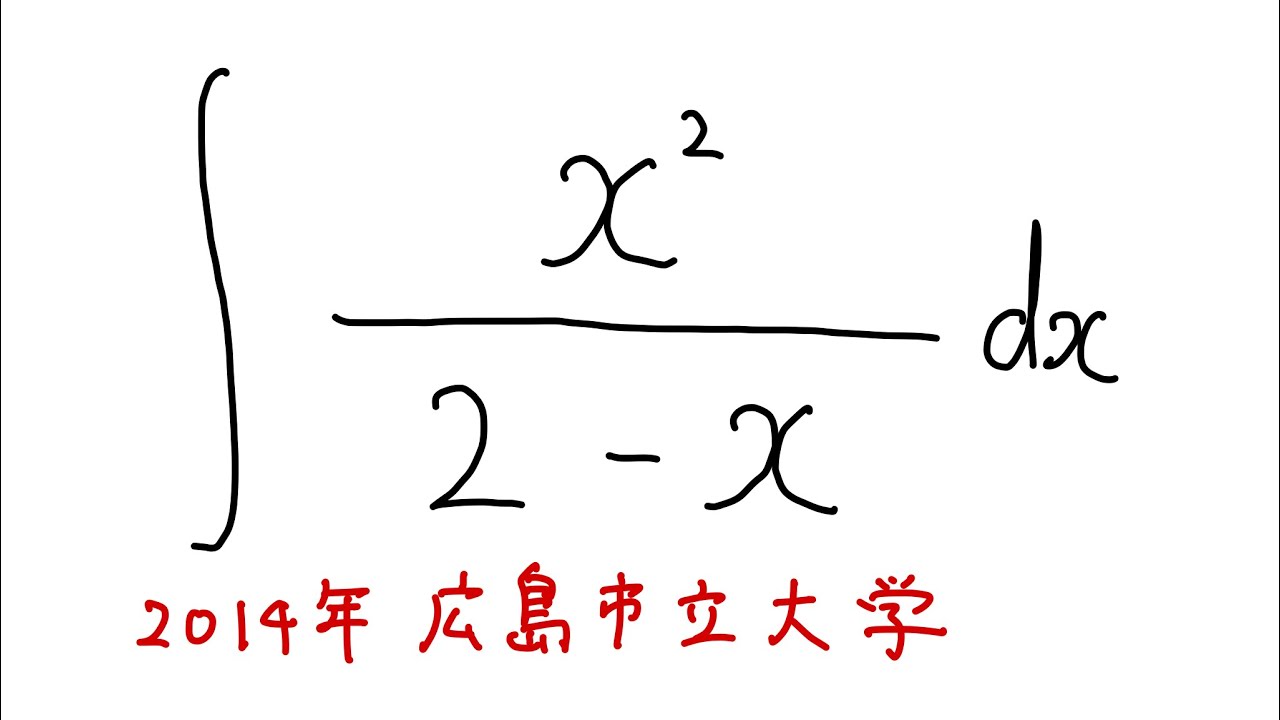
$\displaystyle \int \displaystyle \frac{x^2}{2-x} dx$
出典:2014年広島市立大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x^2}{2-x} dx$
出典:2014年広島市立大学
#電気通信大学2015#定積分#ますただ
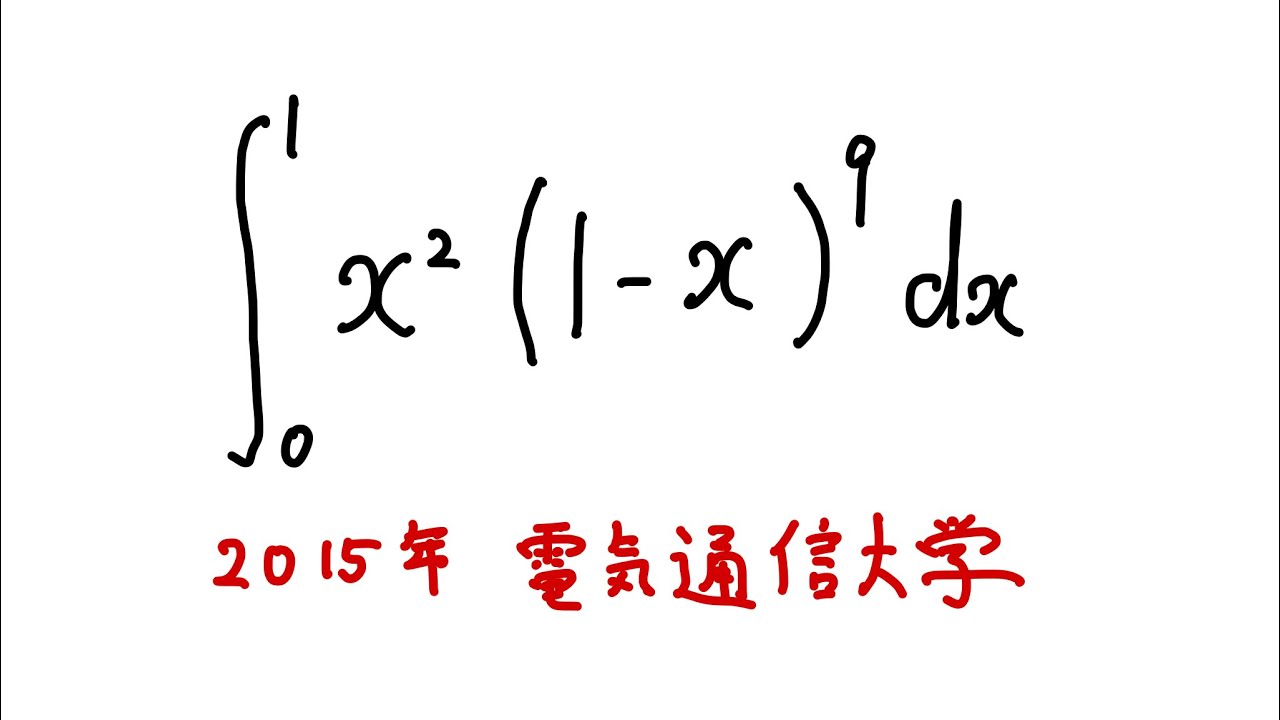
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} x^2(1-x)^9 dx$
出典:2015年電気通信大学
この動画を見る
$\displaystyle \int_{0}^{1} x^2(1-x)^9 dx$
出典:2015年電気通信大学
福田の数学〜筑波大学2024理系第2問〜対数不等式が表す領域と面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#指数関数と対数関数#微分法と積分法#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学
指導講師:
福田次郎
問題文全文(内容文):
(1)$x\gt 1, y\gt 1$のとき、$\log_{ x } y+\log_{ y } x\geqq 2$を示せ。
(2)座標平面において、連立不等式$x\gt 1, y\gt 1, \log_{ x } y+\log_{ y } x\lt \frac{5}{2}$の表す領域を図示せよ。
(3)(2)の領域の中で$x^2+y^2\lt 12$を満たす部分に境界線を含めた図形を$\mathit{D}$とする。$\mathit{D}$の面積を求めよ。
この動画を見る
(1)$x\gt 1, y\gt 1$のとき、$\log_{ x } y+\log_{ y } x\geqq 2$を示せ。
(2)座標平面において、連立不等式$x\gt 1, y\gt 1, \log_{ x } y+\log_{ y } x\lt \frac{5}{2}$の表す領域を図示せよ。
(3)(2)の領域の中で$x^2+y^2\lt 12$を満たす部分に境界線を含めた図形を$\mathit{D}$とする。$\mathit{D}$の面積を求めよ。
大学入試問題#891「まだこのタイプの問題残ってた」 #信州大学(2023) #キングプロパティ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#信州大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\pi}^{ \pi } \displaystyle \frac{1}{1+e^{-2\sin x}} dx$
出典:2023年信州大学
この動画を見る
$\displaystyle \int_{-\pi}^{ \pi } \displaystyle \frac{1}{1+e^{-2\sin x}} dx$
出典:2023年信州大学
中学生にはきついよ 因数分解 東京農大一

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)#東京農工大学
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$4a^4b^4-29a^2b^2+25$
この動画を見る
因数分解せよ
$4a^4b^4-29a^2b^2+25$
#富山大学薬学部2018#不定積分
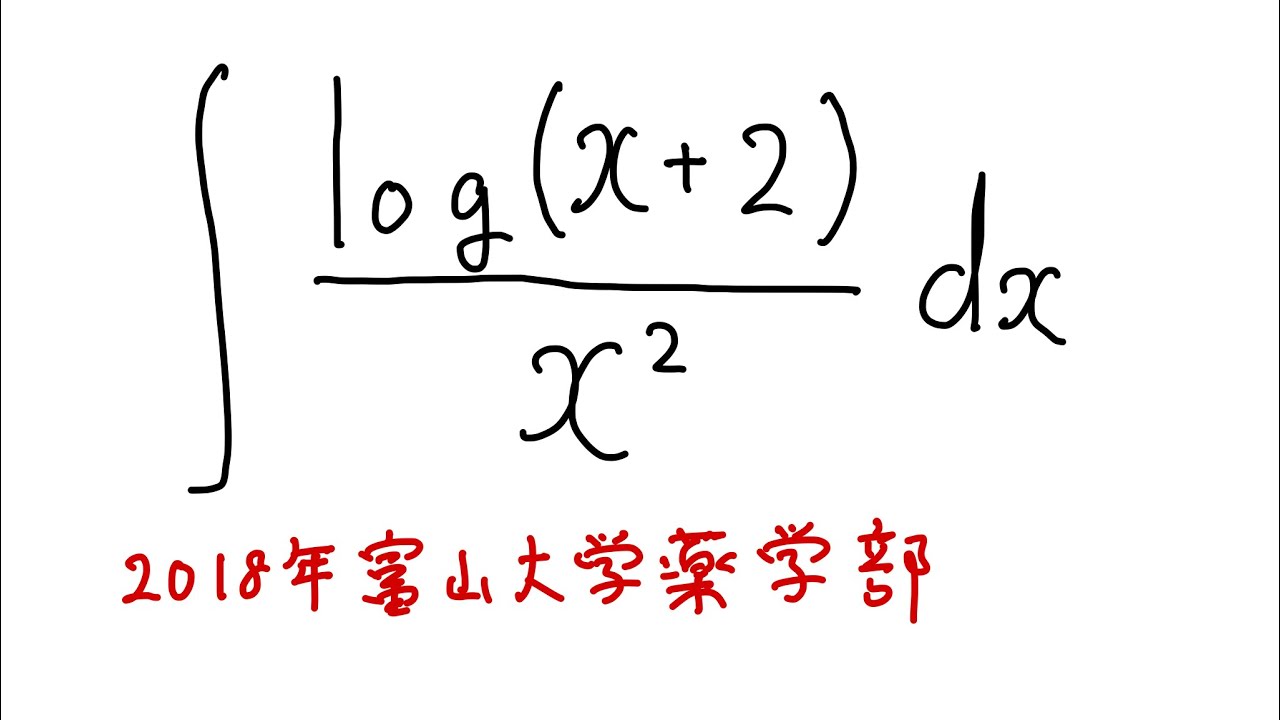
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#富山大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{log(x+2)}{x^2} dx$
出典:2018年富山大学薬学部
この動画を見る
$\displaystyle \int \displaystyle \frac{log(x+2)}{x^2} dx$
出典:2018年富山大学薬学部
大学入試問題#890「苦手な受験生多そう」 #富山大学(2019)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#富山大学
指導講師:
ますただ
問題文全文(内容文):
$f(x)=x\sqrt{ x+1 }$を導関数の定義に従って微分せよ。
出典:2019年富山大学推薦
この動画を見る
$f(x)=x\sqrt{ x+1 }$を導関数の定義に従って微分せよ。
出典:2019年富山大学推薦
