 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
福田の数学〜立教大学2024年経済学部第1問(2)〜恒等式の未定係数を決定する方法

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
等式$\frac{3x^2-x+4}{(x+1)^3}=\frac{a}{(z+1)^3}+\frac{b}{(x+1)^2}+\frac{c}{x+1}$が$x$についての恒等式となるような定数$a, b, c$は$a=\fbox{ウ}, b=\fbox{エ}, c=\fbox{オ}$である。
この動画を見る
等式$\frac{3x^2-x+4}{(x+1)^3}=\frac{a}{(z+1)^3}+\frac{b}{(x+1)^2}+\frac{c}{x+1}$が$x$についての恒等式となるような定数$a, b, c$は$a=\fbox{ウ}, b=\fbox{エ}, c=\fbox{オ}$である。
#藤田保健衛生大学2012 #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$a \gt 0,b \gt 0$
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{\{ax+b(1-x\}^2)} dx$
出典:2010年藤田保健衛生大学
この動画を見る
以下の定積分を解け。
$a \gt 0,b \gt 0$
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{\{ax+b(1-x\}^2)} dx$
出典:2010年藤田保健衛生大学
大学入試問題#873「コメント欄が賑わいそう」 #東京理科大学(2022) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{4} \displaystyle \frac{2}{(x+1)(x+2)(x+3)} dx$
出典:2022年東京理科大学 大学入試問題
この動画を見る
$\displaystyle \int_{0}^{4} \displaystyle \frac{2}{(x+1)(x+2)(x+3)} dx$
出典:2022年東京理科大学 大学入試問題
#自治医科大学2015 #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#自治医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \{\sqrt{ (n+2)(n+3) }-\sqrt{ (n-2)(n-3) }\}$
出典:2015年自治医科大学
この動画を見る
$\displaystyle \lim_{ n \to \infty } \{\sqrt{ (n+2)(n+3) }-\sqrt{ (n-2)(n-3) }\}$
出典:2015年自治医科大学
#関西学院大学2012 #不定積分
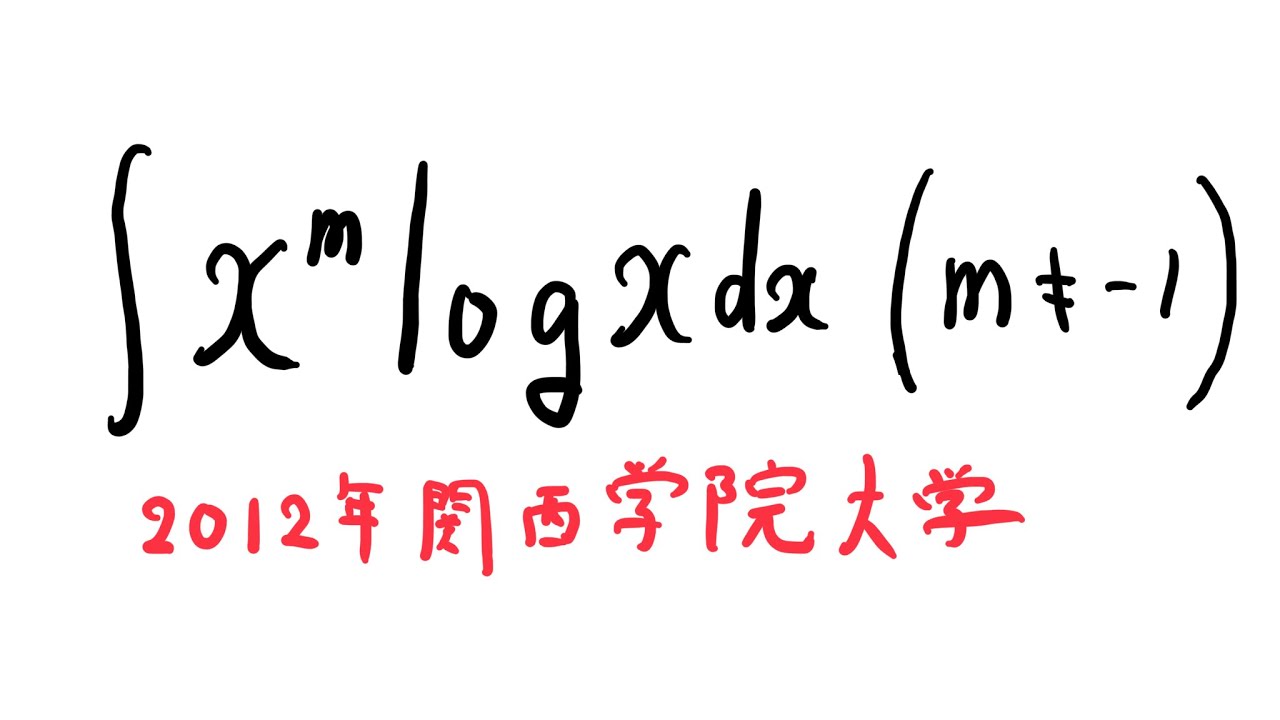
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int x^m log$ $x$ $dx(m \neq -1)$
出典:2012年関西学院大学
この動画を見る
$\displaystyle \int x^m log$ $x$ $dx(m \neq -1)$
出典:2012年関西学院大学
福田の数学〜立教大学2024年経済学部第1問(1)〜対数関数の最小値

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$1\leqq x\leqq 8$の範囲において、関数$y=(\log_{2} x)^2-8\log_{2} x-20$は$x=\fbox{ア}$のときに最小値$\fbox{イ}$をとる。
この動画を見る
$1\leqq x\leqq 8$の範囲において、関数$y=(\log_{2} x)^2-8\log_{2} x-20$は$x=\fbox{ア}$のときに最小値$\fbox{イ}$をとる。
#関西大学2012 #三角関数
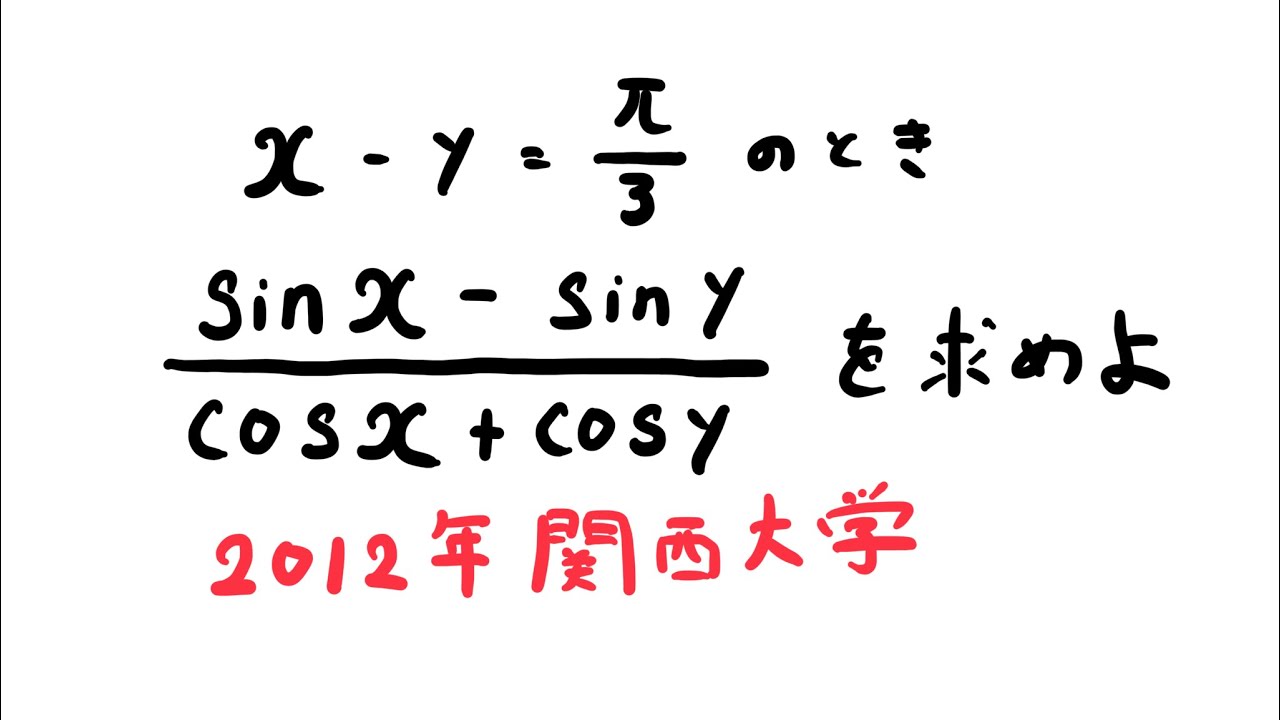
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$x-y=\displaystyle \frac{\pi}{3}$のとき
$\displaystyle \frac{\sin x-\sin y}{\cos x+\cos y}$を求めよ。
出典:2012年関西大学
この動画を見る
$x-y=\displaystyle \frac{\pi}{3}$のとき
$\displaystyle \frac{\sin x-\sin y}{\cos x+\cos y}$を求めよ。
出典:2012年関西大学
大学入試問題#872「受験生は一度は解くべき」 #東北大学医学部AO(2019) #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$a$を実数とする。
次の極限を求めよ。
$\displaystyle \lim_{ n \to \infty } (1+a^{2n})^{\frac{1}{n}}$
出典:2019年東北大学医学部AO
この動画を見る
$a$を実数とする。
次の極限を求めよ。
$\displaystyle \lim_{ n \to \infty } (1+a^{2n})^{\frac{1}{n}}$
出典:2019年東北大学医学部AO
#青山学院大2019 #定積分
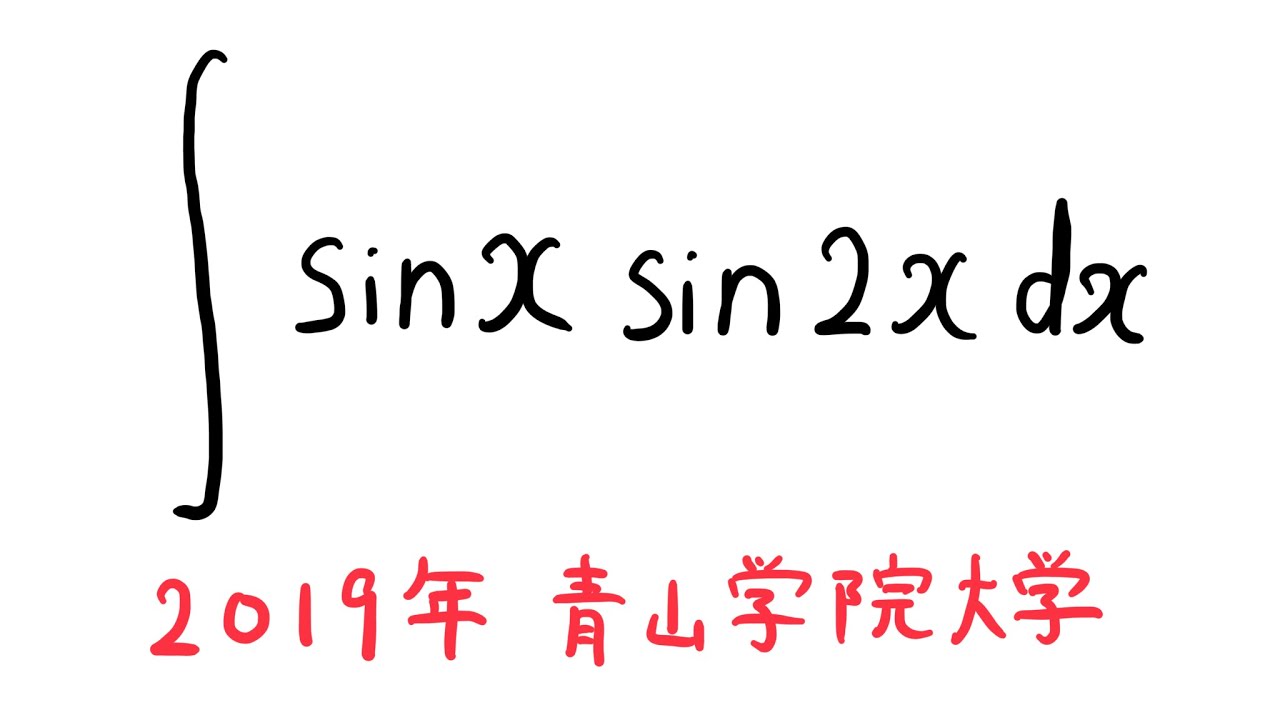
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け。
$\displaystyle \int \sin x \sin 2x$ $dx$
出典:2019年青山学院大学
この動画を見る
以下の不定積分を解け。
$\displaystyle \int \sin x \sin 2x$ $dx$
出典:2019年青山学院大学
福田の数学〜立教大学2024年理学部第4問〜3次方程式の実数解と整数解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$m, a, b, c, d, e, f, r, s, t$を自然数とする。このとき(1)~(5)に答えよ。ただし、(2)(3)の事実は(4)(5)で用いてよい。
(1)2次方程式$2x^2+5x+m=0$の解が有理数となるような自然数$m$をすべて求めよ。ただし、$p$が素数であるとき$\sqrt{p}$が無理数であることを用いてよい。
(2)3次方程式$x^3+ax^2+bx+c=0$の実数解は負の数であることを証明せよ。ただし、方程式$x^3+ax^2+bx+c=0$が少なくとも1つ実数解をもつことは証明せずに用いてよい。
(3)3次方程式$x^3+dx^2+ex+f=0$が整数$n$を解にもつとする。このとき$n$は$f$の約数であることを示せ。
(4)3次方程式$x^3+rx^2+rx+3=0$が整数解を少なくとも1つもつような自然数$r$をすべて求めよ。
(5)3次方程式$x^3+sx^2+tx+6=0$が異なる3つの整数を解にもつような自然数の組$(s, t)$をすべて求めよ。
この動画を見る
$m, a, b, c, d, e, f, r, s, t$を自然数とする。このとき(1)~(5)に答えよ。ただし、(2)(3)の事実は(4)(5)で用いてよい。
(1)2次方程式$2x^2+5x+m=0$の解が有理数となるような自然数$m$をすべて求めよ。ただし、$p$が素数であるとき$\sqrt{p}$が無理数であることを用いてよい。
(2)3次方程式$x^3+ax^2+bx+c=0$の実数解は負の数であることを証明せよ。ただし、方程式$x^3+ax^2+bx+c=0$が少なくとも1つ実数解をもつことは証明せずに用いてよい。
(3)3次方程式$x^3+dx^2+ex+f=0$が整数$n$を解にもつとする。このとき$n$は$f$の約数であることを示せ。
(4)3次方程式$x^3+rx^2+rx+3=0$が整数解を少なくとも1つもつような自然数$r$をすべて求めよ。
(5)3次方程式$x^3+sx^2+tx+6=0$が異なる3つの整数を解にもつような自然数の組$(s, t)$をすべて求めよ。
大学入試問題#871「初手が大事な基本問題」 #日本工業大学(2023) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{\sqrt{ 3 }} \displaystyle \frac{2x^2-x+2}{x^3+x} dx$
出典:2023年日本工業大学
この動画を見る
$\displaystyle \int_{1}^{\sqrt{ 3 }} \displaystyle \frac{2x^2-x+2}{x^3+x} dx$
出典:2023年日本工業大学
#自治医科大(2015) #定積分 #Shorts

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#自治医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \frac{35}{2}\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^7x$ $dx$
出典:2015年自治医科大学
この動画を見る
$\displaystyle \frac{35}{2}\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^7x$ $dx$
出典:2015年自治医科大学
#青山学院大学(2006) #定積分 #Shorts
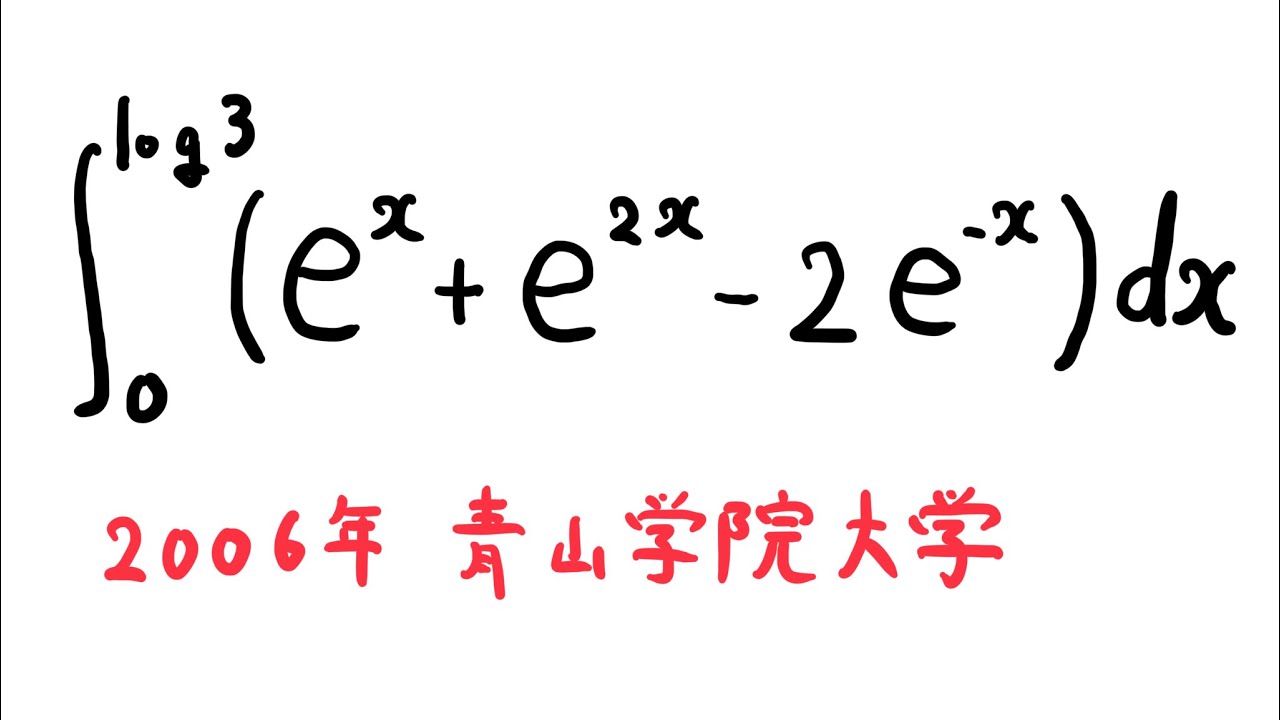
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{log3} (e^x+e^{2x}-2e^{-x}) dx$
出典:2006年青山学院大学
この動画を見る
$\displaystyle \int_{0}^{log3} (e^x+e^{2x}-2e^{-x}) dx$
出典:2006年青山学院大学
大学入試問題#870「基本問題」 #東北大学医学部AO(2019) #数列

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$S_n=2a_n+3n$を満たす数列$\{a_n\}$の一般項$a_n$を求めよ。
出典:2019年東北大学医学部AO
この動画を見る
$S_n=2a_n+3n$を満たす数列$\{a_n\}$の一般項$a_n$を求めよ。
出典:2019年東北大学医学部AO
福田の数学〜立教大学2024年理学部第3問〜放物線のx軸周りとy軸周りの回転体の体積バームクーヘン積分
単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}O$を原点とする座標平面上に放物線$C:y=x-x^2$がある。$C$上の点$P(\frac{1}{2},\frac{1}{4})$における$C$の接線を$l$、$Q(1,0)$における$C$の接線を$m$とする。$l$と$y$軸、$m$と$y$軸の交点をそれぞれR、Sとする。
(1)$l,m$の方程式をそれぞれ求めよ。
(2)$C$の$0\leqq x \leqq 1$の部分と、2つの線分QS,OSで囲まれた図形の面積Aを求めよ。
(3)$C$の$0 leqq x \leqq 1$の部分と、線分OQで囲まれた図形を、$x$軸のまわりに1回転させてできる立体の体積$V_1$を求めよ。
(4)$C$の$0 \leqq x \leqq \frac{1}{2}$の部分と、2つの線分PR,ORで囲まれた図形を、$y$軸のまわりに1回転させてできる立体$V_2$を求めよ。
(5)$C$の$0 \leqq x \leqq 1$の部分と、線分OQで囲まれた図形を、$y$軸のまわりに1回転させてできる立体の体積$V_3$を求めよ。
この動画を見る
$\boxed{3}O$を原点とする座標平面上に放物線$C:y=x-x^2$がある。$C$上の点$P(\frac{1}{2},\frac{1}{4})$における$C$の接線を$l$、$Q(1,0)$における$C$の接線を$m$とする。$l$と$y$軸、$m$と$y$軸の交点をそれぞれR、Sとする。
(1)$l,m$の方程式をそれぞれ求めよ。
(2)$C$の$0\leqq x \leqq 1$の部分と、2つの線分QS,OSで囲まれた図形の面積Aを求めよ。
(3)$C$の$0 leqq x \leqq 1$の部分と、線分OQで囲まれた図形を、$x$軸のまわりに1回転させてできる立体の体積$V_1$を求めよ。
(4)$C$の$0 \leqq x \leqq \frac{1}{2}$の部分と、2つの線分PR,ORで囲まれた図形を、$y$軸のまわりに1回転させてできる立体$V_2$を求めよ。
(5)$C$の$0 \leqq x \leqq 1$の部分と、線分OQで囲まれた図形を、$y$軸のまわりに1回転させてできる立体の体積$V_3$を求めよ。
大学入試問題#868「ヒントがあれば、どうってことない」 #埼玉医科大学(2010) #式変形

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉医科大学
指導講師:
ますただ
問題文全文(内容文):
$a \leq b \leq c$とする。
$\sqrt{ 10+\sqrt{ 24 }+\sqrt{ 40 }+\sqrt{ 60 } }=\sqrt{ a }+\sqrt{ b }+\sqrt{ c }=$であるとき、$a,b,c$の値を求めよ。
出典:2010年埼玉医科大学
この動画を見る
$a \leq b \leq c$とする。
$\sqrt{ 10+\sqrt{ 24 }+\sqrt{ 40 }+\sqrt{ 60 } }=\sqrt{ a }+\sqrt{ b }+\sqrt{ c }=$であるとき、$a,b,c$の値を求めよ。
出典:2010年埼玉医科大学
大学入試問題#867「これは、過去1番の難問かも」 #産業医科大学(2012) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{ 1-2\sin 2x+3\cos^2x }$ $dx$
出典:2012年産業医科大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{ 1-2\sin 2x+3\cos^2x }$ $dx$
出典:2012年産業医科大学
大学入試問題#866「まあ、なんとかなるわな」 #東京女子医科大学(2005) #式変形

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$(1-\sqrt[ 3 ]{ 2 }+\sqrt[ 3 ]{ 4 })^8$を計算せよ
出典:2005年東京女子医科大学
この動画を見る
$(1-\sqrt[ 3 ]{ 2 }+\sqrt[ 3 ]{ 4 })^8$を計算せよ
出典:2005年東京女子医科大学
福田の数学〜立教大学2024年理学部第1問(2)〜17のn乗の1の位

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (2)$17^n$の1の位の数が1になる最小の自然数$n$は$\boxed{\ \ イ\ \ }$である。また、$17^{555}$の1の位の数を求めると、$\boxed{\ \ ウ\ \ }$である。
この動画を見る
$\Large{\boxed{1}}$ (2)$17^n$の1の位の数が1になる最小の自然数$n$は$\boxed{\ \ イ\ \ }$である。また、$17^{555}$の1の位の数を求めると、$\boxed{\ \ ウ\ \ }$である。
大学入試問題#865「中学生の問題か!?」 #岩手医科大学(2008) #方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x-1)(y-1)=9 \\
x+y-\sqrt{ x^2+xy+y^2 }=1
\end{array}
\right.
\end{eqnarray}$を解け。
出典:2008年岩手医科大学
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x-1)(y-1)=9 \\
x+y-\sqrt{ x^2+xy+y^2 }=1
\end{array}
\right.
\end{eqnarray}$を解け。
出典:2008年岩手医科大学
福田の数学〜立教大学2024年理学部第1問(1)〜三角方程式の基本

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (1)実数$x$が$3\cos x$=$\sin^2x$ を満たすとき、$\cos x$の値は$\boxed{\ \ ア\ \ }$である。
この動画を見る
$\Large{\boxed{1}}$ (1)実数$x$が$3\cos x$=$\sin^2x$ を満たすとき、$\cos x$の値は$\boxed{\ \ ア\ \ }$である。
大学入試問題#864「基本に忠実に」 #宮崎大学(2013) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{e^{4x}}{e^{2x}+2} dx$
出典:2013年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{e^{4x}}{e^{2x}+2} dx$
出典:2013年宮崎大学 入試問題
福田の数学〜慶應義塾大学2024年経済学部第6問〜3次関数の増減と最大値と面積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{6}}$ $a$,$b$,$p$を実数とする。関数$f(x)$=$x^3$+$ax^2$+$bx$+17 は$x$=$p$で極大値、$x$=$-4p$で極小値をとり、$f(-2p)$=-17 を満たすとする。
(1)$a$,$b$,$p$の値、および$f(x)$の極大値$M$、極大値$m$を、それぞれ求めよ。
(2)(1)で求めた$a$,$b$および0≦$t$≦5 を満たす実数$t$に対して、区間0≦$x$≦$t$ における|$f(x)$|の最大値を$g(t)$とする。$t$の値について場合分けをして、それぞれの場合に$g(t)$を求めよ。
(3)(2)で求めた$g(t)$に対して、定積分$I$=$\displaystyle\int_0^5g(t)dt$ を求めよ。
この動画を見る
$\Large{\boxed{6}}$ $a$,$b$,$p$を実数とする。関数$f(x)$=$x^3$+$ax^2$+$bx$+17 は$x$=$p$で極大値、$x$=$-4p$で極小値をとり、$f(-2p)$=-17 を満たすとする。
(1)$a$,$b$,$p$の値、および$f(x)$の極大値$M$、極大値$m$を、それぞれ求めよ。
(2)(1)で求めた$a$,$b$および0≦$t$≦5 を満たす実数$t$に対して、区間0≦$x$≦$t$ における|$f(x)$|の最大値を$g(t)$とする。$t$の値について場合分けをして、それぞれの場合に$g(t)$を求めよ。
(3)(2)で求めた$g(t)$に対して、定積分$I$=$\displaystyle\int_0^5g(t)dt$ を求めよ。
福田のおもしろ数学182〜2x3x5x7x11x13の10乗の桁数

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$(2×3×5×7×11×13)^{10}$ の10進法での桁数を求めよ。
この動画を見る
$(2×3×5×7×11×13)^{10}$ の10進法での桁数を求めよ。
福田の数学〜慶應義塾大学2024年経済学部第5問〜ある対数とそれを超えない最大の整数

単元:
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{5}}$ $x$を正の実数とする。$m$と$n$は、それぞれ$m$≦$\displaystyle\log_4\frac{x}{8}$, $n$≦$\displaystyle\log_2\frac{8}{x}$ を満たす最大の整数とし、さらに、$\alpha$=$\displaystyle\log_4\frac{x}{8}$-$m$, $\beta$=$\displaystyle\log_2\frac{8}{x}$-$n$ とおく。
(1)$\log_2x$を、$m$と$\alpha$を用いて表せ。
(2)$2\alpha$+$\beta$ の取りうる値を全て求めよ。
(3)$n$=$m$-1 のとき、$m$と$n$の値を求めよ。
(4)$n$=$m$-1 となるために$x$が満たすべき必要十分条件を求めよ。
この動画を見る
$\Large{\boxed{5}}$ $x$を正の実数とする。$m$と$n$は、それぞれ$m$≦$\displaystyle\log_4\frac{x}{8}$, $n$≦$\displaystyle\log_2\frac{8}{x}$ を満たす最大の整数とし、さらに、$\alpha$=$\displaystyle\log_4\frac{x}{8}$-$m$, $\beta$=$\displaystyle\log_2\frac{8}{x}$-$n$ とおく。
(1)$\log_2x$を、$m$と$\alpha$を用いて表せ。
(2)$2\alpha$+$\beta$ の取りうる値を全て求めよ。
(3)$n$=$m$-1 のとき、$m$と$n$の値を求めよ。
(4)$n$=$m$-1 となるために$x$が満たすべき必要十分条件を求めよ。
福田の数学〜慶應義塾大学2024年経済学部第4問〜正四面体の位置ベクトルと面積体積

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{4}}$ $p$,$q$を正の実数とし、Oを原点とする座標空間内に3点A(3,$-\sqrt 3$,0),B(3,$\sqrt 3$,0),C($p$,0,$q$)をとる。ただし、四面体OABCは1辺の長さが$2\sqrt 3$の正四面体であるとする。
(1)$p$および$q$の値を求めよ。
以下、点$\displaystyle\left(\frac{3}{2},0,\frac{q}{2}\right)$に関してO,A,B,Cと対称な点を、それぞれD,E,F,Gとする。
(2)直線DGと平面ABCとの交点Hの座標を求めよ。
(3)直線CBと平面DEGとの交点をI、直線CAと平面DFGとの交点をJとする。
四角形CJHIの面積$S$と四角錐G-CJHIの体積$V$を、それぞれ求めよ。
この動画を見る
$\Large{\boxed{4}}$ $p$,$q$を正の実数とし、Oを原点とする座標空間内に3点A(3,$-\sqrt 3$,0),B(3,$\sqrt 3$,0),C($p$,0,$q$)をとる。ただし、四面体OABCは1辺の長さが$2\sqrt 3$の正四面体であるとする。
(1)$p$および$q$の値を求めよ。
以下、点$\displaystyle\left(\frac{3}{2},0,\frac{q}{2}\right)$に関してO,A,B,Cと対称な点を、それぞれD,E,F,Gとする。
(2)直線DGと平面ABCとの交点Hの座標を求めよ。
(3)直線CBと平面DEGとの交点をI、直線CAと平面DFGとの交点をJとする。
四角形CJHIの面積$S$と四角錐G-CJHIの体積$V$を、それぞれ求めよ。
大学入試問題#863「ごちゃごちゃしとる」 #産業医科大学(2012) #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \{\sqrt[ 3 ]{ (n^3-n^2)^2 }-2n\sqrt[ 3 ]{ n^3-n^2 }+n^2$
出典:2012年産業医科大学
この動画を見る
$\displaystyle \lim_{ n \to \infty } \{\sqrt[ 3 ]{ (n^3-n^2)^2 }-2n\sqrt[ 3 ]{ n^3-n^2 }+n^2$
出典:2012年産業医科大学
福田の数学〜慶應義塾大学2024年経済学部第3問〜指数関数で定義された数列の漸化式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ 実数$a$に対して$f(a)$=$\displaystyle\frac{1}{2}(2^a-2^{-a})$とおく。また、$A$=$2^a$とする。
(1)等式$\displaystyle\left(A-\frac{1}{A}\right)^3$=$\displaystyle\boxed{\ \ ア\ \ }\left(A-\frac{1}{A}\right)^3$-$\displaystyle\boxed{\ \ イ\ \ }\left(A-\frac{1}{A}\right)$ より、実数$a$に対して
$\left\{f(a)\right\}^3$=$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}f(3a)$-$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}f(a)$ ...①が成り立つ。
(2)実数$a$,$b$に対して$f(a)$=$b$が成り立つならば、$A$=$2^a$は2次方程式
$A^2$-$\boxed{\ \ キ\ \ }bA$-$\boxed{\ \ ク\ \ }$=0
を満たす。$2^a$>0より、$a$は$b$を用いて
$a$=$\log_2\left(\boxed{\ \ ケ\ \ }b+\sqrt{b^2+\boxed{\ \ コ\ \ }}\right)$ ...②
と表せる。つまり、任意の実数bに対して$f(a)$=$b$となる実数$a$が、ただ1つに定まる。
以下、数列$\left\{a_n\right\}$に対して$f(a_n)$=$b_n$ ($n$=1,2,3,...)で定まる数列$\left\{b_n\right\}$が、関係式
$4b_{n+1}^3$+$3b_{n+1}$-$b_n$=0 ($n$=1,2,3,...) ...③
を満たすとする。
(3)①と③から$f\left(\boxed{\ \ サ\ \ }a_{n+1}\right)$=$f(a_n)$ ($n$=1,2,3,...)となるので、(2)より、
$a_n$=$\displaystyle\frac{a_1}{\boxed{\ \ シ\ \ }^{n-p}}$ ($n$=1,2,3,...)が得られる。ここで、$p$=$\boxed{\ \ ス\ \ }$である。
(4)$n$≧2に対して、$S_n$=$\displaystyle\sum_{k=2}^n3^{k-1}b_k^3$ とおく。$c_n$=$3^nb_n$ ($n$=1,2,3,...)で定まる数列$\left\{c_n\right\}$の階差数列を用いると、③より、
$S_n$=$\frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソ\ \ }}b_1$-$\frac{\boxed{\ \ タ\ \ }^n}{\boxed{\ \ チ\ \ }}b_n$ ($n$=2,3,4,...)
となる。ゆえに、$b_1$=$\displaystyle\frac{4}{3}S_5$-108 が成り立つならば$a_1$=$\boxed{\ \ ツテト\ \ }\log_2\boxed{\ \ ナ\ \ }$ である。
この動画を見る
$\Large{\boxed{3}}$ 実数$a$に対して$f(a)$=$\displaystyle\frac{1}{2}(2^a-2^{-a})$とおく。また、$A$=$2^a$とする。
(1)等式$\displaystyle\left(A-\frac{1}{A}\right)^3$=$\displaystyle\boxed{\ \ ア\ \ }\left(A-\frac{1}{A}\right)^3$-$\displaystyle\boxed{\ \ イ\ \ }\left(A-\frac{1}{A}\right)$ より、実数$a$に対して
$\left\{f(a)\right\}^3$=$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}f(3a)$-$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}f(a)$ ...①が成り立つ。
(2)実数$a$,$b$に対して$f(a)$=$b$が成り立つならば、$A$=$2^a$は2次方程式
$A^2$-$\boxed{\ \ キ\ \ }bA$-$\boxed{\ \ ク\ \ }$=0
を満たす。$2^a$>0より、$a$は$b$を用いて
$a$=$\log_2\left(\boxed{\ \ ケ\ \ }b+\sqrt{b^2+\boxed{\ \ コ\ \ }}\right)$ ...②
と表せる。つまり、任意の実数bに対して$f(a)$=$b$となる実数$a$が、ただ1つに定まる。
以下、数列$\left\{a_n\right\}$に対して$f(a_n)$=$b_n$ ($n$=1,2,3,...)で定まる数列$\left\{b_n\right\}$が、関係式
$4b_{n+1}^3$+$3b_{n+1}$-$b_n$=0 ($n$=1,2,3,...) ...③
を満たすとする。
(3)①と③から$f\left(\boxed{\ \ サ\ \ }a_{n+1}\right)$=$f(a_n)$ ($n$=1,2,3,...)となるので、(2)より、
$a_n$=$\displaystyle\frac{a_1}{\boxed{\ \ シ\ \ }^{n-p}}$ ($n$=1,2,3,...)が得られる。ここで、$p$=$\boxed{\ \ ス\ \ }$である。
(4)$n$≧2に対して、$S_n$=$\displaystyle\sum_{k=2}^n3^{k-1}b_k^3$ とおく。$c_n$=$3^nb_n$ ($n$=1,2,3,...)で定まる数列$\left\{c_n\right\}$の階差数列を用いると、③より、
$S_n$=$\frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソ\ \ }}b_1$-$\frac{\boxed{\ \ タ\ \ }^n}{\boxed{\ \ チ\ \ }}b_n$ ($n$=2,3,4,...)
となる。ゆえに、$b_1$=$\displaystyle\frac{4}{3}S_5$-108 が成り立つならば$a_1$=$\boxed{\ \ ツテト\ \ }\log_2\boxed{\ \ ナ\ \ }$ である。
大学入試問題#862「一言、よくある良問」 #横浜国立大学 #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2} x^3\sqrt{ 4-x^2 } dx$
出典:横浜国立大学
この動画を見る
$\displaystyle \int_{0}^{2} x^3\sqrt{ 4-x^2 } dx$
出典:横浜国立大学
福田の数学〜慶應義塾大学2024年経済学部第2問〜確率の基本性質と非復元抽出の条件付き確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ 袋の中に、1から9までの番号を重複なく1つずつ記入したカードが9枚入っている。A,B,C,Dの4人のうちDがさいころを投げて、1の目が出たらAが、2または3の目が出たらBが、その他の目が出たらCが、袋の中からカードを1枚引き、カードに記入された番号を記録することを試行という。ただし、1度引いたカードは袋に戻さない。この試行を3回続けて行う。また、1回目の試行前のA,B,Cの点数をそれぞれ0としたうえで、以下の(a),(b)に従い、各回の試行後のA,B,Cの点数を定める。
(a)各回の試行においてカードを引いた人は、その回の試行前の自分の点数に、その回の試行で記録した番号を加え、試行後の点数とする。
(b)各回の試行においてカードを引いていない人は、その回の試行前の自分の点数を、そのまま試行後の点数とする。
(1)1回目の試行後、Bの点数が3の倍数となる確率は$\frac{\boxed{ア}}{\boxed{イ}}$である。ただし、0はすべての整数の倍数である。
(2)2回目の試行後、A,B,Cのうち、1人だけの点数が0である確率は$\frac{\boxed{ウエ}}{\boxed{オカ}}$である。
(3)2回目の試行後のAの点数が5以上となる確率は$\frac{\boxed{キク}}{\boxed{ケコ}}$である。
(4)2回目の試行後のAの点数が5以上であるとき、3回目の試行後のA,B,Cの点数がすべて5以上である条件付き確率は$\frac{\boxed{サシ}}{\boxed{スセソ}}$である。
この動画を見る
$\Large{\boxed{2}}$ 袋の中に、1から9までの番号を重複なく1つずつ記入したカードが9枚入っている。A,B,C,Dの4人のうちDがさいころを投げて、1の目が出たらAが、2または3の目が出たらBが、その他の目が出たらCが、袋の中からカードを1枚引き、カードに記入された番号を記録することを試行という。ただし、1度引いたカードは袋に戻さない。この試行を3回続けて行う。また、1回目の試行前のA,B,Cの点数をそれぞれ0としたうえで、以下の(a),(b)に従い、各回の試行後のA,B,Cの点数を定める。
(a)各回の試行においてカードを引いた人は、その回の試行前の自分の点数に、その回の試行で記録した番号を加え、試行後の点数とする。
(b)各回の試行においてカードを引いていない人は、その回の試行前の自分の点数を、そのまま試行後の点数とする。
(1)1回目の試行後、Bの点数が3の倍数となる確率は$\frac{\boxed{ア}}{\boxed{イ}}$である。ただし、0はすべての整数の倍数である。
(2)2回目の試行後、A,B,Cのうち、1人だけの点数が0である確率は$\frac{\boxed{ウエ}}{\boxed{オカ}}$である。
(3)2回目の試行後のAの点数が5以上となる確率は$\frac{\boxed{キク}}{\boxed{ケコ}}$である。
(4)2回目の試行後のAの点数が5以上であるとき、3回目の試行後のA,B,Cの点数がすべて5以上である条件付き確率は$\frac{\boxed{サシ}}{\boxed{スセソ}}$である。
