 教員採用試験
教員採用試験
 教員採用試験
教員採用試験
13神奈川県教員採用試験(数学:9番 数列の極限値)

単元:
#関数と極限#数列の極限#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
9⃣$a_1=1,a_2=2,(a_{n+2})^5 =(a_{n+1})^4・a_n$
$\displaystyle \lim_{ n \to \infty } a_n$を求めよ。
この動画を見る
9⃣$a_1=1,a_2=2,(a_{n+2})^5 =(a_{n+1})^4・a_n$
$\displaystyle \lim_{ n \to \infty } a_n$を求めよ。
13神奈川県教員採用試験(数学:11番 曲線の長さ)

単元:
#積分とその応用#面積・体積・長さ・速度#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{11}$曲線$6y^2=x(2-x)^2 $ $(0 \leqq x \leqq 2)$
の長さlを求めよ。
この動画を見る
$\boxed{11}$曲線$6y^2=x(2-x)^2 $ $(0 \leqq x \leqq 2)$
の長さlを求めよ。
13神奈川県教員採用試験(数学:8番 行列)

単元:
#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
8⃣ $A=\begin{pmatrix}
-1 & -3 \\
1 & 2
\end{pmatrix}$
$S=A+A^2+\cdots+A^{99}$を求めよ。
この動画を見る
8⃣ $A=\begin{pmatrix}
-1 & -3 \\
1 & 2
\end{pmatrix}$
$S=A+A^2+\cdots+A^{99}$を求めよ。
13神奈川県教員採用試験(数学:4番 整式の割り算)

13兵庫県教員採用試験(数学:2番 微分)

単元:
#数Ⅱ#微分法と積分法#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣
$C_1:y=x^2-4x+36$ , $C_2:y=4x^2+8x$の共通接線の方程式を求めよ。
この動画を見る
2⃣
$C_1:y=x^2-4x+36$ , $C_2:y=4x^2+8x$の共通接線の方程式を求めよ。
10兵庫県教員採用試験(数学:2番 整数問題)

単元:
#数A#整数の性質#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣ $n \in \mathbb{N} $ , $\sqrt n$の整数部分をA(n)
(1)A(10)を求めよ。
(2)A(n)=3をみたすnの個数
(3)$A(1)+A(2)+A(3)+\cdots+A(n)$
この動画を見る
2⃣ $n \in \mathbb{N} $ , $\sqrt n$の整数部分をA(n)
(1)A(10)を求めよ。
(2)A(n)=3をみたすnの個数
(3)$A(1)+A(2)+A(3)+\cdots+A(n)$
15兵庫県教員採用試験(数学:3番 微積)

単元:
#数Ⅱ#微分法と積分法#その他#面積、体積#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
3⃣ $k>0$ , $C:f(x)=x^3-3k^2x$
Cは極大値16をもつ。C上の点(1,f(1))の接線lとCで囲まれた面積Sを求めよ。
この動画を見る
3⃣ $k>0$ , $C:f(x)=x^3-3k^2x$
Cは極大値16をもつ。C上の点(1,f(1))の接線lとCで囲まれた面積Sを求めよ。
19奈良県教員採用試験(数学:2番 三角関数)

単元:
#数Ⅱ#三角関数#三角関数とグラフ#接線と増減表・最大値・最小値#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣$0 \leqq θ \leqq \pi$
$y= sin2θ + 2(sinθ+cosθ)-i$のMAX、minとそのときのθの値を求めよ。
この動画を見る
2⃣$0 \leqq θ \leqq \pi$
$y= sin2θ + 2(sinθ+cosθ)-i$のMAX、minとそのときのθの値を求めよ。
08大阪府教員採用試験(数学:1番 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣ $n \in \mathbb {Z}$
$n^5-n$が30の倍数である
この動画を見る
1⃣ $n \in \mathbb {Z}$
$n^5-n$が30の倍数である
19奈良県教員採用試験(数学:高2番 微積)

単元:
#積分とその応用#面積・体積・長さ・速度#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣ $f(x)=x-e^x$
x=t,x=t+1,x軸で囲まれた面積をS(t)とする。
S(t)の最小値を求めよ。
この動画を見る
2⃣ $f(x)=x-e^x$
x=t,x=t+1,x軸で囲まれた面積をS(t)とする。
S(t)の最小値を求めよ。
18奈良県教員採用試験(数学:4番 複素数)

単元:
#複素数平面#複素数平面#その他#数学(高校生)#数C#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
4⃣ $x^3-1=0$の虚数解の1つをw
(1)$\displaystyle \sum_{k=1}^{3N} w^{k-1}$
(2)$\displaystyle \sum_{k=0}^{3N} {}_{3N}C_kw^k$
この動画を見る
4⃣ $x^3-1=0$の虚数解の1つをw
(1)$\displaystyle \sum_{k=1}^{3N} w^{k-1}$
(2)$\displaystyle \sum_{k=0}^{3N} {}_{3N}C_kw^k$
10東京都教員採用試験(数学:1-6番 微分方程式)

単元:
#微分とその応用#その他#速度と近似式#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣(6)$(x+2) \frac{dy}{dx} = -(y+3)$
x=0のときy=0をみたす特殊解を求めよ。
この動画を見る
1⃣(6)$(x+2) \frac{dy}{dx} = -(y+3)$
x=0のときy=0をみたす特殊解を求めよ。
16神奈川県教員採用試験(数学:6番 指数対数)
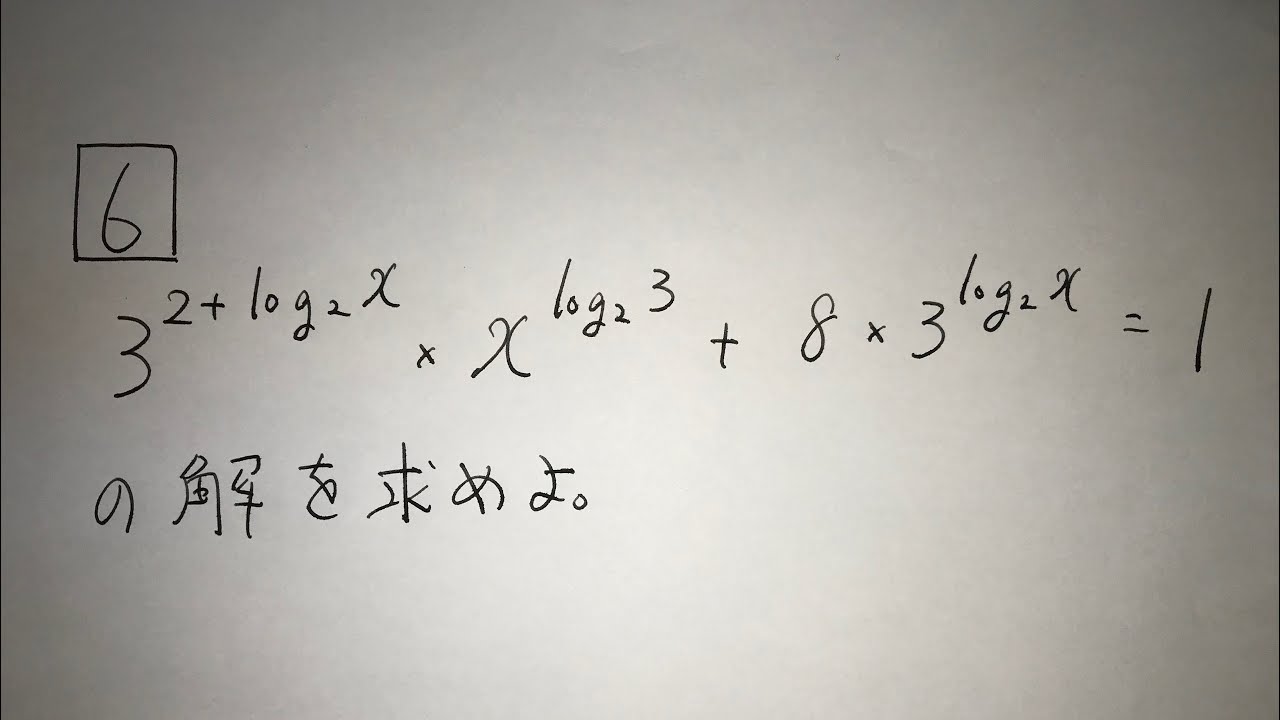
単元:
#数Ⅱ#指数関数と対数関数#指数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
6⃣
$3^{2+log_2x}×x^{log_23}+8×3^{log_2x}=1$の解を求めよ。
この動画を見る
6⃣
$3^{2+log_2x}×x^{log_23}+8×3^{log_2x}=1$の解を求めよ。
15神奈川県教員採用試験(数学:8番 行列)

単元:
#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
8⃣一次変換$f=\begin{pmatrix}
3 & 2 \\
t & -1
\end{pmatrix}$,
$g=\begin{pmatrix}
2 & 1 \\
-3 & -1
\end{pmatrix}$
$f^{-1}・g(p)=\begin{pmatrix}
-1 \\
2
\end{pmatrix}$をみたすPの座標を求めよ。
この動画を見る
8⃣一次変換$f=\begin{pmatrix}
3 & 2 \\
t & -1
\end{pmatrix}$,
$g=\begin{pmatrix}
2 & 1 \\
-3 & -1
\end{pmatrix}$
$f^{-1}・g(p)=\begin{pmatrix}
-1 \\
2
\end{pmatrix}$をみたすPの座標を求めよ。
13東京都教員採用試験(数学:6番 複素数)
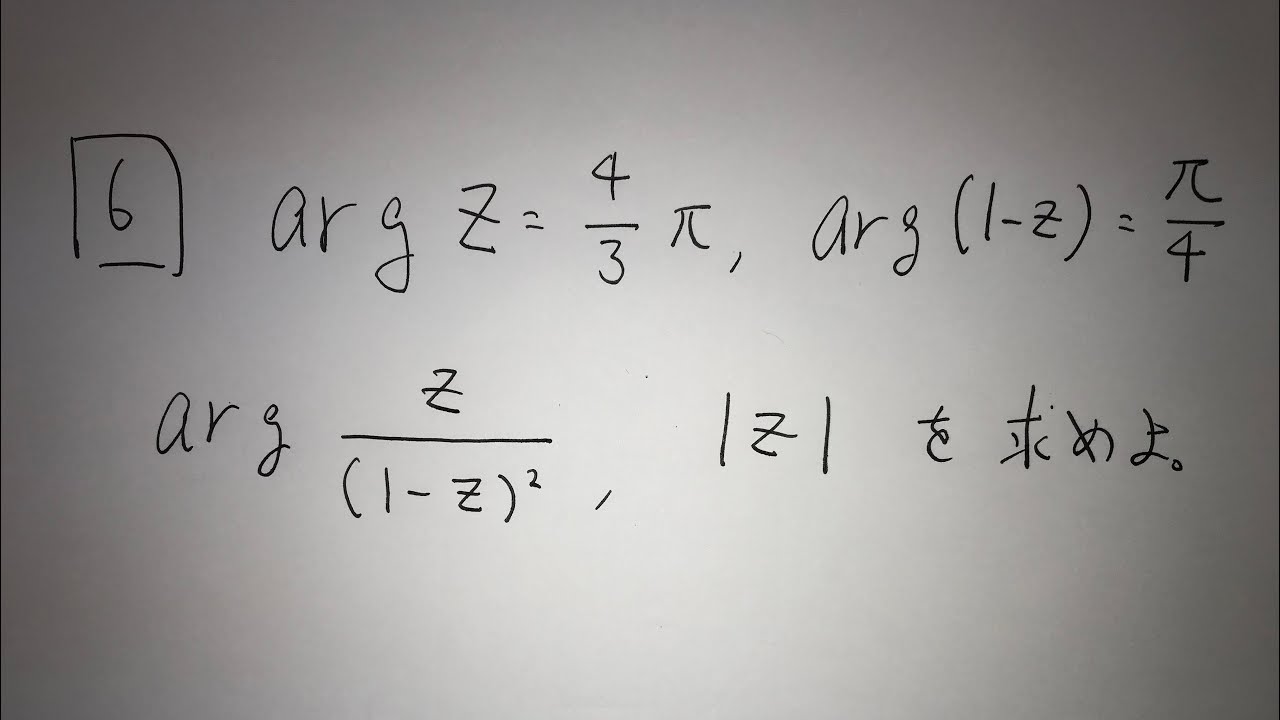
単元:
#複素数平面#複素数平面#その他#数学(高校生)#数C#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
6⃣$argZ=\frac{4}{3} \pi$ , $arg(1-z)=\frac{\pi}{4}$
$arg \frac{z}{(1-z)^2}$ , |z|を求めよ。
この動画を見る
6⃣$argZ=\frac{4}{3} \pi$ , $arg(1-z)=\frac{\pi}{4}$
$arg \frac{z}{(1-z)^2}$ , |z|を求めよ。
13東京都教員採用試験(数学:7番 偏微分)
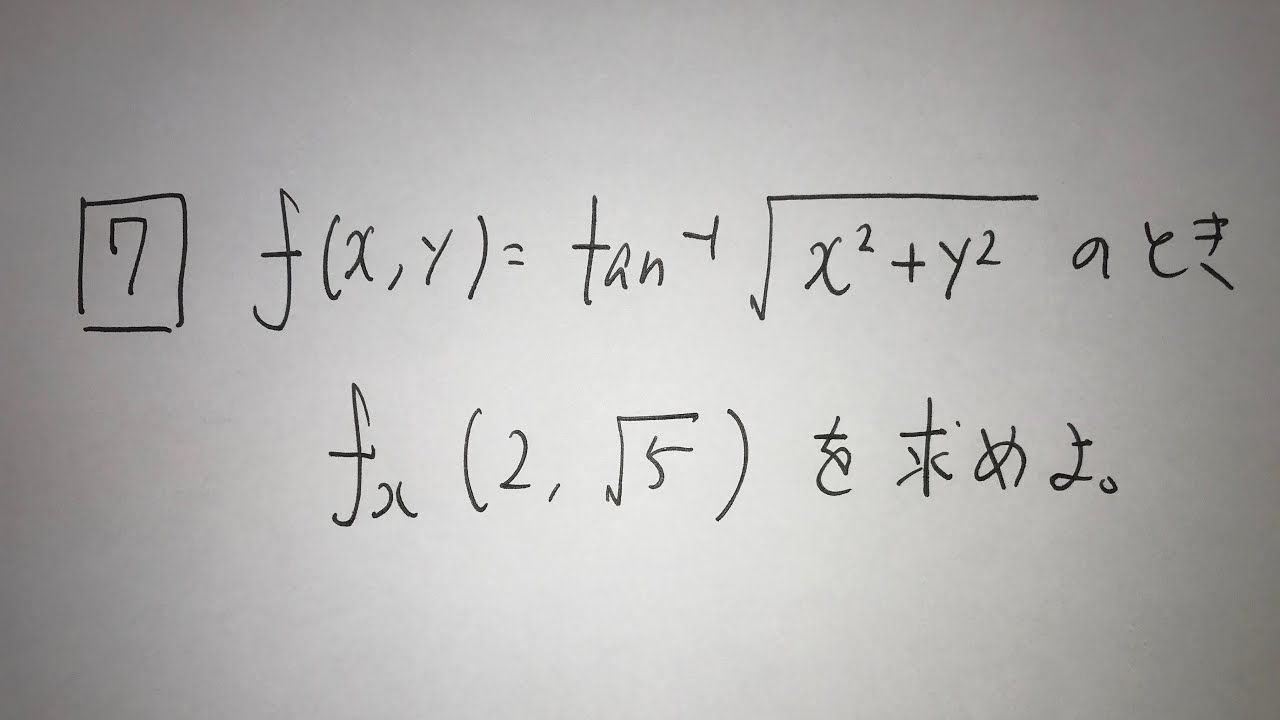
単元:
#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
7⃣$f(x,y)=tan^{-1} \sqrt{x^2+y^2}$のとき$f_x$(2,5)を求めよ。
この動画を見る
7⃣$f(x,y)=tan^{-1} \sqrt{x^2+y^2}$のとき$f_x$(2,5)を求めよ。
13東京都教員採用試験(数学:5番 微分)
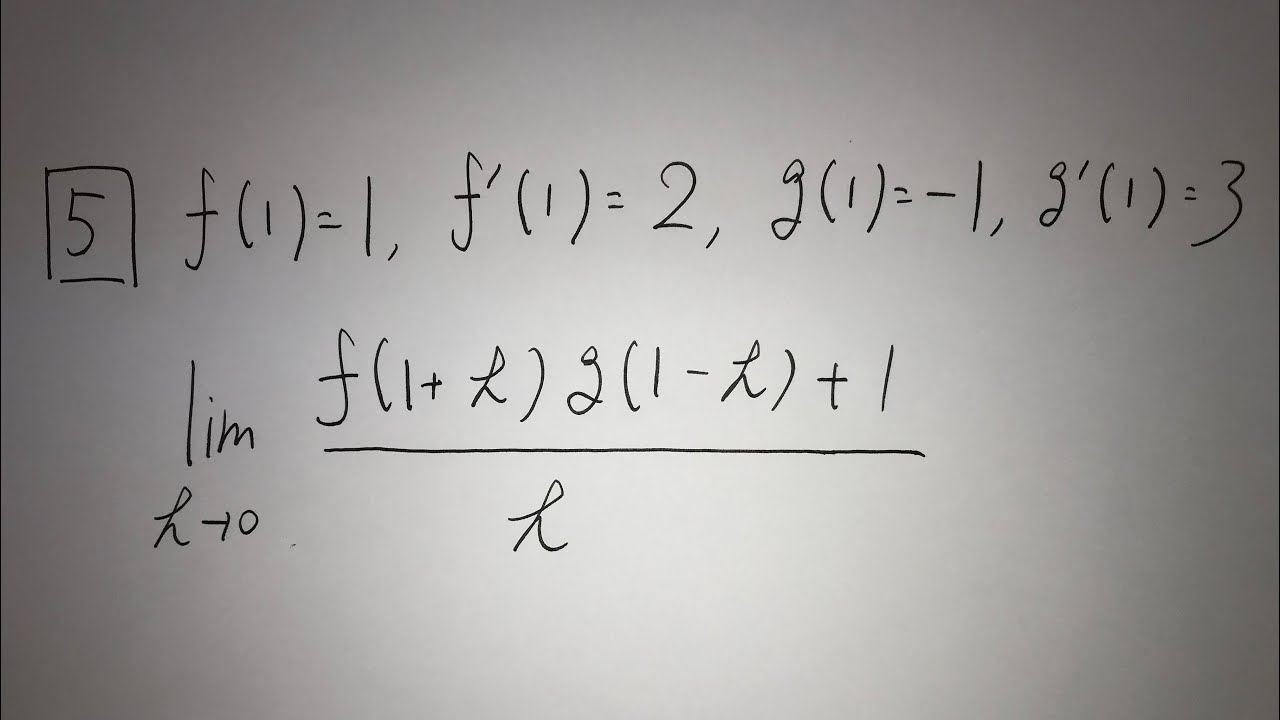
単元:
#微分とその応用#微分法#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
5⃣$f(1)=1$ , $f'(1)=2$ , $g(1)=-1$ , $g(1)=3$
$\displaystyle \lim_{ h \to 0 } \frac{f(1+h)g(1-h)+1}{h}$
この動画を見る
5⃣$f(1)=1$ , $f'(1)=2$ , $g(1)=-1$ , $g(1)=3$
$\displaystyle \lim_{ h \to 0 } \frac{f(1+h)g(1-h)+1}{h}$
17愛知県教員採用試験(数学:1-2番 整数問題)

単元:
#数Ⅰ#数A#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(2)
$\frac{n}{225} < 1$ $(n \in \mathbb{N})$をみたす既約分数の個数
この動画を見る
1⃣-(2)
$\frac{n}{225} < 1$ $(n \in \mathbb{N})$をみたす既約分数の個数
17愛知県教員採用試験(数学:1番 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣ $x,y \in \mathbb{N}$
(1)$xy+3x-2y=30$をみたす(x,y)
(2)$x^3-xy-2y+2=0$をみたす(x,y)
この動画を見る
1⃣ $x,y \in \mathbb{N}$
(1)$xy+3x-2y=30$をみたす(x,y)
(2)$x^3-xy-2y+2=0$をみたす(x,y)
08神奈川県教員採用試験(数学:6番 微分方程式)
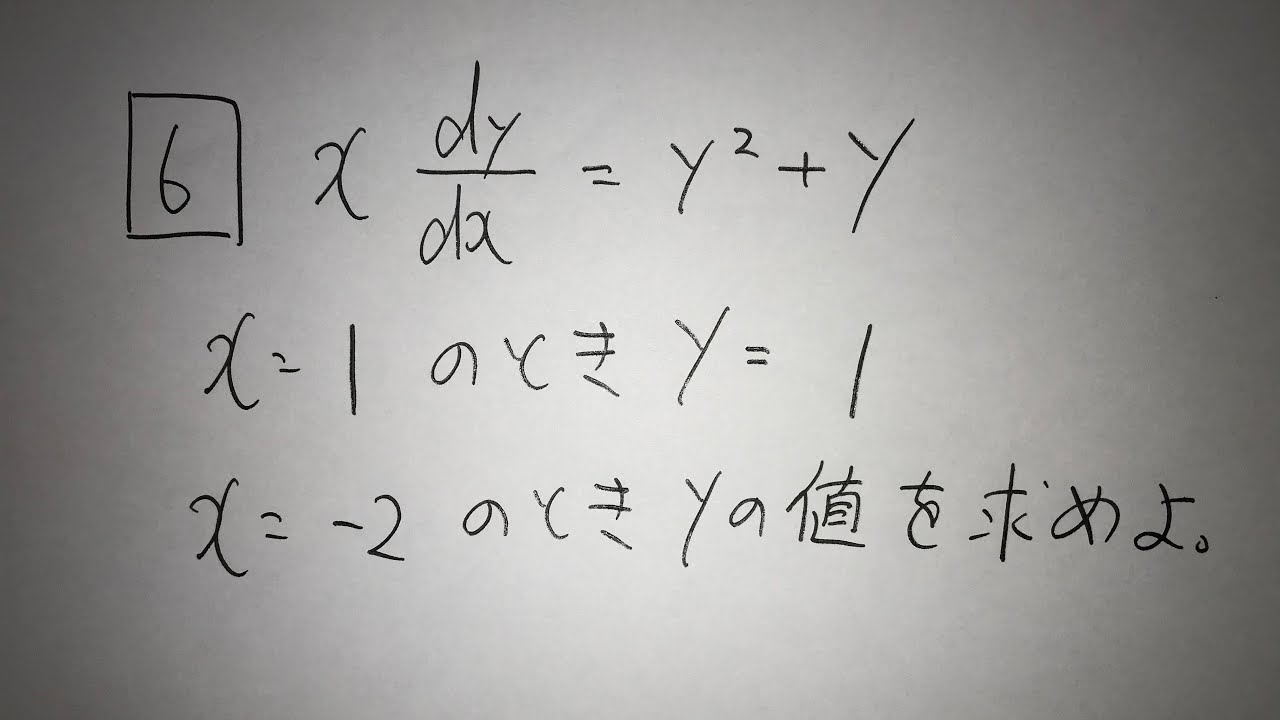
単元:
#微分とその応用#その他#速度と近似式#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
6⃣ $x \frac{dy}{dx} = y^2+y$
x=1のときy=1である。
x=-2のときyの値を求めよ。
この動画を見る
6⃣ $x \frac{dy}{dx} = y^2+y$
x=1のときy=1である。
x=-2のときyの値を求めよ。
11京都府教員採用試験(数学:3番 微分方程式)
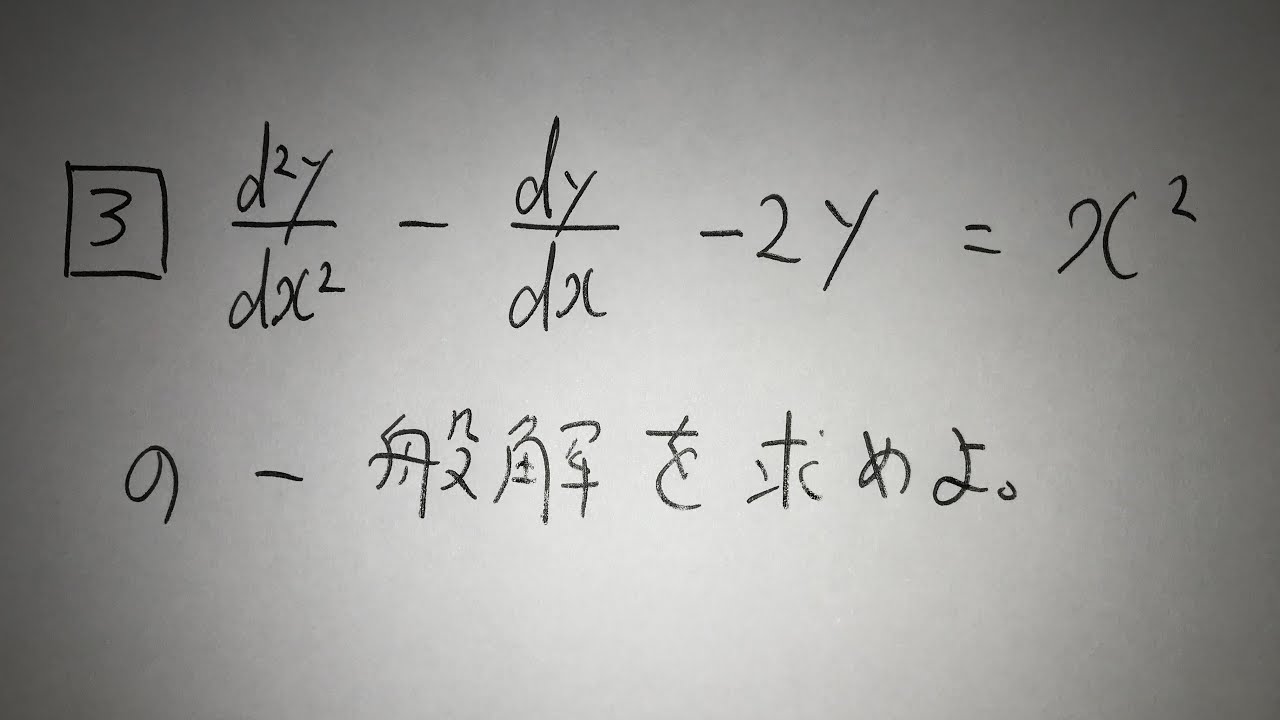
単元:
#微分とその応用#その他#速度と近似式#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
3⃣ $\frac{d^2y}{dx^2} - \frac{dy}{dx} - 2y=x^2$の一般解を求めよ。
この動画を見る
3⃣ $\frac{d^2y}{dx^2} - \frac{dy}{dx} - 2y=x^2$の一般解を求めよ。
12神奈川県教員採用試験(数学:12番 微分方程式)

単元:
#微分とその応用#その他#速度と近似式#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{12}$
$\frac{dy}{dx} = \frac{y}{x}+\frac{2x}{y}$ $(x=e , y=e^2)$
x=1のときy(x>0)を求めよ。
この動画を見る
$\boxed{12}$
$\frac{dy}{dx} = \frac{y}{x}+\frac{2x}{y}$ $(x=e , y=e^2)$
x=1のときy(x>0)を求めよ。
14奈良県教員採用試験(数学:2-1番 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣-(1)
$\sqrt{n^2+211}$が整数となる$n \in \mathbb{ N }$を求めよ。
この動画を見る
2⃣-(1)
$\sqrt{n^2+211}$が整数となる$n \in \mathbb{ N }$を求めよ。
15東京都教員採用試験(数学:1-3 複素数)
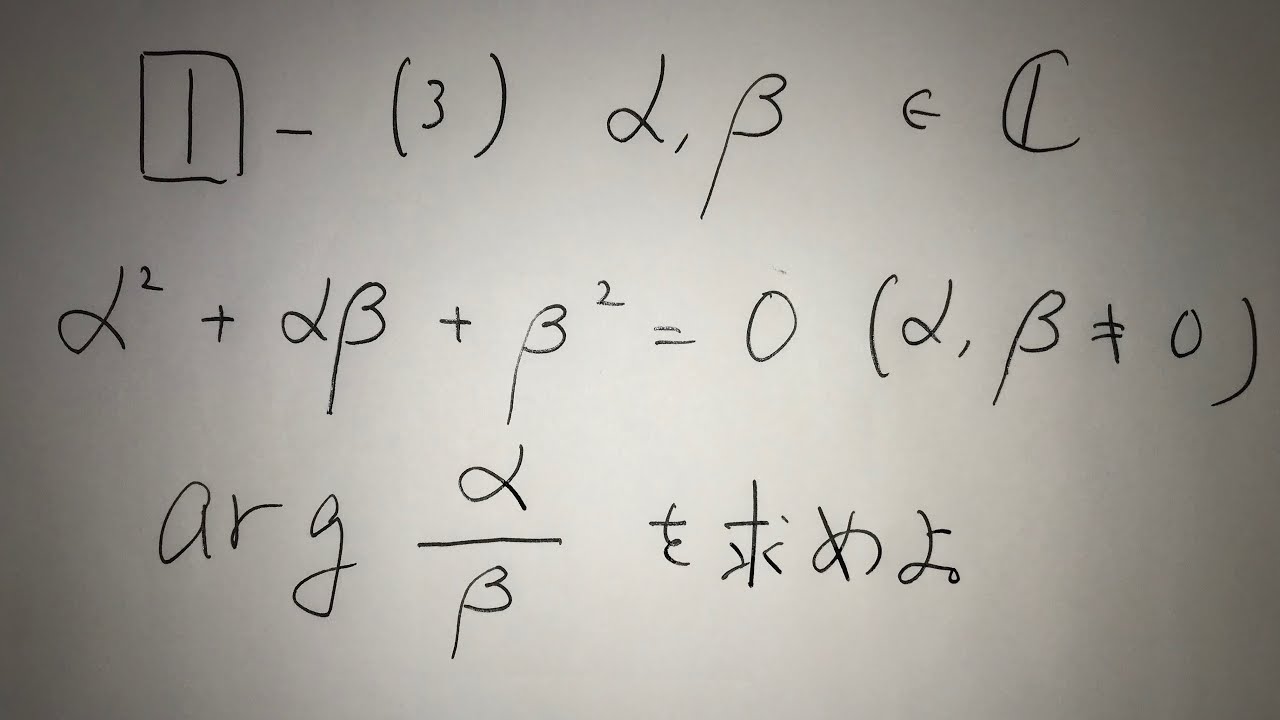
単元:
#複素数平面#複素数平面#その他#数学(高校生)#数C#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(3)
$α、β \in \mathbb{ C }$
$α^2+αβ+β^2=0$ (α,β≠0)
$arg \frac{α}{β}$
この動画を見る
1⃣-(3)
$α、β \in \mathbb{ C }$
$α^2+αβ+β^2=0$ (α,β≠0)
$arg \frac{α}{β}$
15東京都教員採用試験(数学:1-1 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(1)
$m^2-mn+3m-3n-7=0$
をみたす自然数の組(m,n)を求めよ。
この動画を見る
1⃣-(1)
$m^2-mn+3m-3n-7=0$
をみたす自然数の組(m,n)を求めよ。
12奈良県教員採用試験(数学:1-4番 定積分)
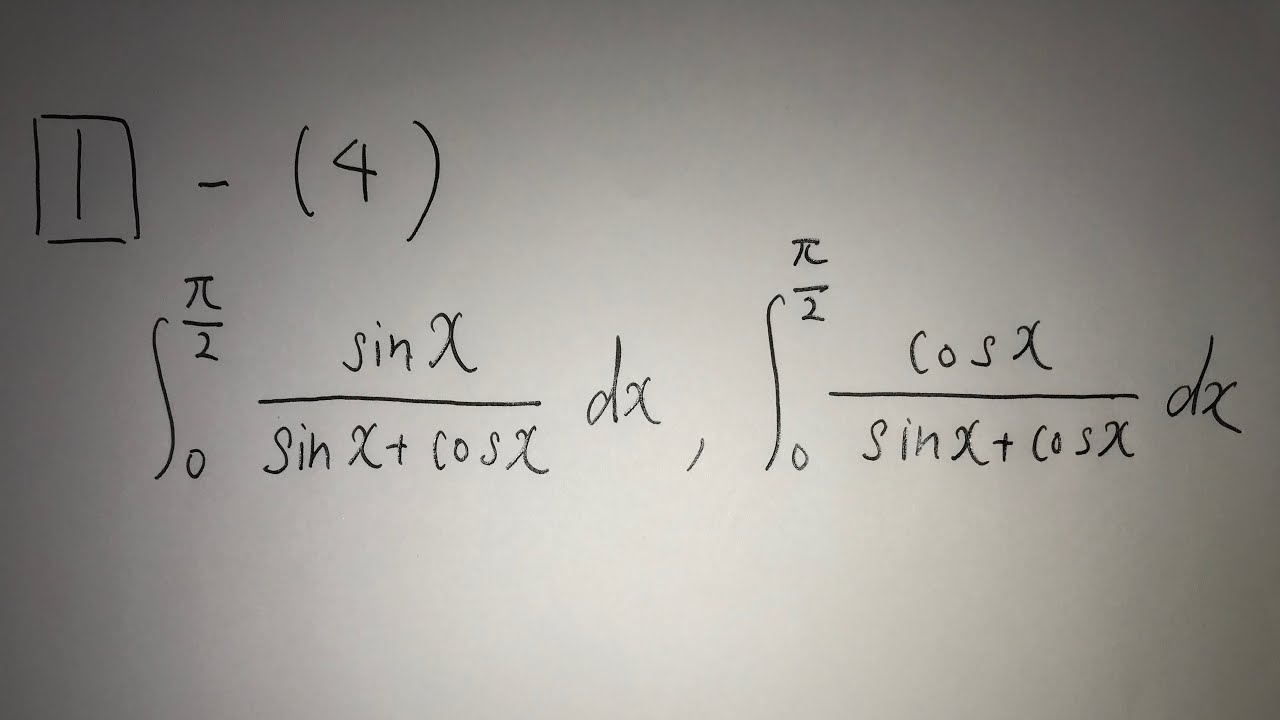
単元:
#積分とその応用#定積分#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(4)
$\int_0^\frac{\pi}{2} \frac{sinx}{sinx+cosx}dx$ , $\int_0^\frac{\pi}{2} \frac{cosx}{sinx+cosx}dx$
kingproperty
$\int_a^b f(x) dx = \int_a^b f(a+b-x) dx$
この動画を見る
1⃣-(4)
$\int_0^\frac{\pi}{2} \frac{sinx}{sinx+cosx}dx$ , $\int_0^\frac{\pi}{2} \frac{cosx}{sinx+cosx}dx$
kingproperty
$\int_a^b f(x) dx = \int_a^b f(a+b-x) dx$
13奈良県教員採用試験(数学:1-2番 数列)

単元:
#数列#漸化式#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(2)
$a_1$=3 , $a_2$=2
$a_n=\frac{2a_{n+1}・a_{n-1}}{a_{n+1}+a_{n-1}}$のとき$a_n$を求めよ。
この動画を見る
1⃣-(2)
$a_1$=3 , $a_2$=2
$a_n=\frac{2a_{n+1}・a_{n-1}}{a_{n+1}+a_{n-1}}$のとき$a_n$を求めよ。
13奈良県教員採用試験(数学:1-1番 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(1)
$\frac{1}{x}+\frac{2}{y}=\frac{1}{4}$を満たす正の整数の組(x,y)を求めよ。
この動画を見る
1⃣-(1)
$\frac{1}{x}+\frac{2}{y}=\frac{1}{4}$を満たす正の整数の組(x,y)を求めよ。
15奈良県教員採用試験(数学:中-4番 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
中-4⃣
$x^2-2xy+2y^2-2x-3y+5=0$を満たす整数x,yの組を求めよ。
この動画を見る
中-4⃣
$x^2-2xy+2y^2-2x-3y+5=0$を満たす整数x,yの組を求めよ。
13奈良県教員採用試験(数学:1-3番 2変数の極限)
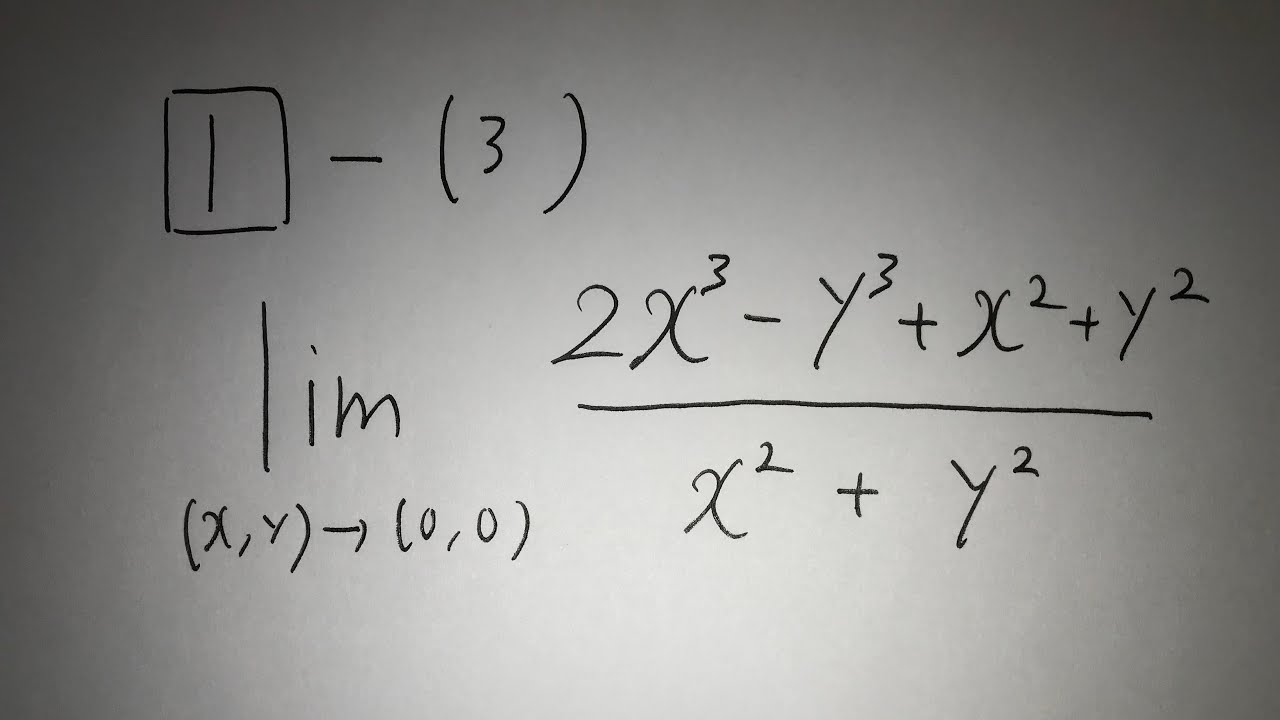
単元:
#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(3)
$\displaystyle \lim_{ (x,y) \to (0,0) } \frac{2x^3-y^3+x^2+y^2}{x^2+y^2}$
この動画を見る
1⃣-(3)
$\displaystyle \lim_{ (x,y) \to (0,0) } \frac{2x^3-y^3+x^2+y^2}{x^2+y^2}$
