 三角比への応用(正弦・余弦・面積)
三角比への応用(正弦・余弦・面積)
 三角比への応用(正弦・余弦・面積)
三角比への応用(正弦・余弦・面積)
【数Ⅰ】【図形と計量】底面の半径が4、高さが2√5の直円錐がある。この直円錐の頂点をO、底面の直径の両端をA、Bとし、線分OBの中点をPとするとき、側面上でAから Pに至る最短距離を求めよ。

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
底面の半径が4、高さが2√5の直円錐がある。この直円錐の頂点をO、底面の直径の両端をA、Bとし、線分OBの中点をPとするとき、側面上でAから Pに至る最短距離を求めよ。
この動画を見る
底面の半径が4、高さが2√5の直円錐がある。この直円錐の頂点をO、底面の直径の両端をA、Bとし、線分OBの中点をPとするとき、側面上でAから Pに至る最短距離を求めよ。
【数Ⅰ】【図形と計量】ヘロンの公式を用いて、次のような△ABCの面積を求めよ。(1) a=3、b=5、c=6(2) a=2、b=3、c=4

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ヘロンの公式を用いて、次のような△ABCの面積を求めよ。
(1) a=3、b=5、c=6
(2) a=2、b=3、c=4
この動画を見る
ヘロンの公式を用いて、次のような△ABCの面積を求めよ。
(1) a=3、b=5、c=6
(2) a=2、b=3、c=4
【数Ⅰ】【図形と計量】△ABCにおいて、次の等式が成り立つとき、この三角形はどのような形をしているか。(1) b * sin B = c * sin C(2) (sin A + sin B + sin

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
△ABCにおいて、次の等式が成り立つとき、この三角形はどのような形をし
ているか。
(1) b * sin B = c * sin C
(2) (sin A + sin B + sin C)(b + c - a) = 2c * sin B
(3) a * cos A + b * cos B = c * cos C
この動画を見る
△ABCにおいて、次の等式が成り立つとき、この三角形はどのような形をし
ているか。
(1) b * sin B = c * sin C
(2) (sin A + sin B + sin C)(b + c - a) = 2c * sin B
(3) a * cos A + b * cos B = c * cos C
【数Ⅰ】【図形と計量】(1) c(sin² A + sin² B) = (a * sin A + b * sin B) * sin C(2) 2(bc * cos A + ca * cos B +

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
△ABCにおいて、次の等式が成り立つことを証明せよ。
(1) c(sin² A + sin² B) = (a * sin A + b * sin B) * sin C
(2) 2(bc * cos A + ca * cos B + ab * cos C) = a ² + b² + c ²
この動画を見る
△ABCにおいて、次の等式が成り立つことを証明せよ。
(1) c(sin² A + sin² B) = (a * sin A + b * sin B) * sin C
(2) 2(bc * cos A + ca * cos B + ab * cos C) = a ² + b² + c ²
【数Ⅰ】【図形と計量】(1) 0° < A < 180° 0°<B <180° sin A = sin B が成り立つとき、 A = B であるといえるか。

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1) 0° < A < 180° 0°<B <180° sin A = sin B が成り立つとき、 A = B であるといえるか。
(2) △ABCにおいて, sinA=sinB が成り立つとき、この三角形は a = b の二等辺三角形であるといえるか。
この動画を見る
(1) 0° < A < 180° 0°<B <180° sin A = sin B が成り立つとき、 A = B であるといえるか。
(2) △ABCにおいて, sinA=sinB が成り立つとき、この三角形は a = b の二等辺三角形であるといえるか。
【高校数学】三角比を使った三角形の面積の求め方 3-9【数学Ⅰ】

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
【高校数学】三角比を使った三角形の面積の求め方を解説していきます。
$\triangle ABC$の面積$S$を求めよ。
(1)$b=4,c=7,A=45°$
(2)$a=7,b=5,c=8$
この動画を見る
【高校数学】三角比を使った三角形の面積の求め方を解説していきます。
$\triangle ABC$の面積$S$を求めよ。
(1)$b=4,c=7,A=45°$
(2)$a=7,b=5,c=8$
【数Ⅰ】【図形と計量】sinθ+cosθ=1/3のとき(1) sinθcosθの値(2) sin³θ+cos³θの値(3) sinθ-cosθの値

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
sinθ+cosθ=1/3のとき
(1) sinθcosθの値
(2) sin³θ+cos³θの値
(3) sinθ-cosθの値
この動画を見る
sinθ+cosθ=1/3のとき
(1) sinθcosθの値
(2) sin³θ+cos³θの値
(3) sinθ-cosθの値
【数Ⅰ】【図形と計量】(1)cos36°を求めよ(2)正五角形の対角線の長さを求めよ。

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)cos36°を求めよ
(2)正五角形の対角線の長さを求めよ。
この動画を見る
(1)cos36°を求めよ
(2)正五角形の対角線の長さを求めよ。
福田のおもしろ数学509〜幾何の証明
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
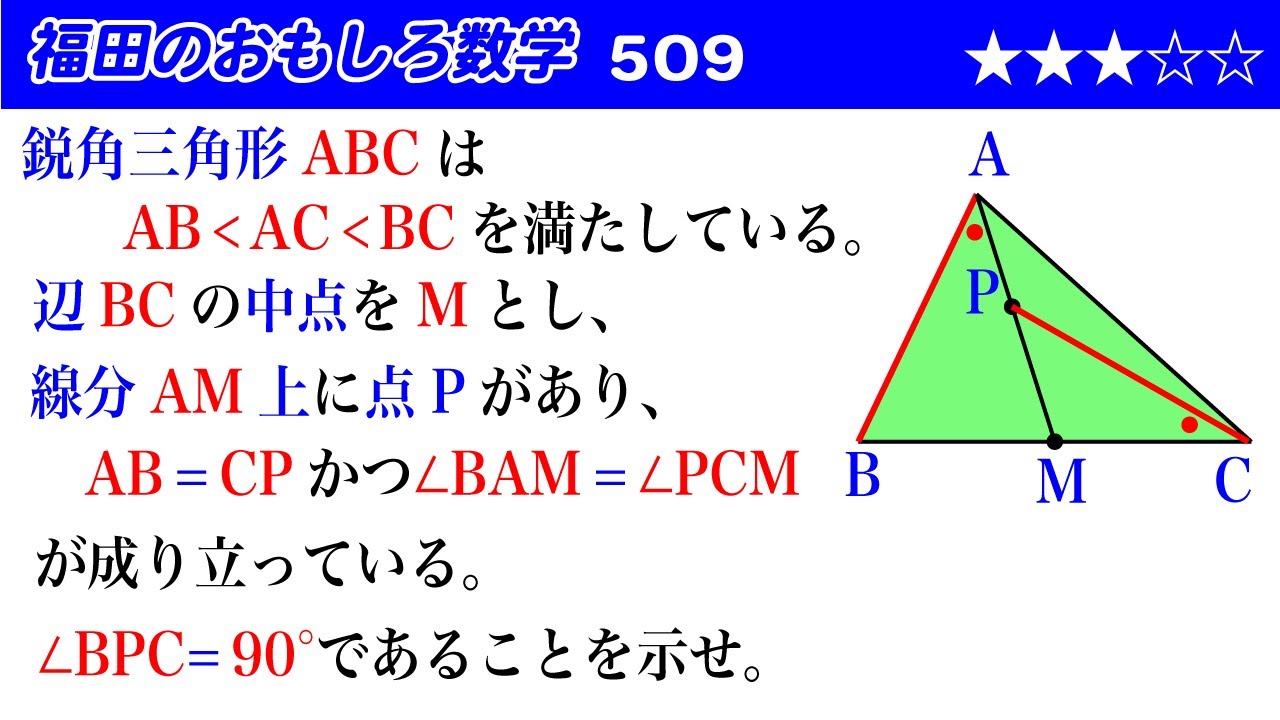
鋭角三角形$ABC$は
$AB \lt AC \lt BC$を満たしている。
辺$BC$の中点を$M$とし、
線分$AM$上に点$P$があり、
$AB = CP$かつ$\angle BAM=\angle PCM$が
成り立っている。
$\angle BPC=90°$であることを示せ。
図は動画内参照
この動画を見る
鋭角三角形$ABC$は
$AB \lt AC \lt BC$を満たしている。
辺$BC$の中点を$M$とし、
線分$AM$上に点$P$があり、
$AB = CP$かつ$\angle BAM=\angle PCM$が
成り立っている。
$\angle BPC=90°$であることを示せ。
図は動画内参照
福田の数学〜北海道大学2025文系第2問〜数え上げと余弦定理

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
整数$a,b,c$は条件
$2\leqq a \lt b \lt c \leqq 6$を満たすとする。
(1)不等式$a+b\gt c$を満たすような
$(a+b+c)$をすべて挙げよ。
(2)不等式$a^2+b^2\geqq c^2$を満たすような
$(a+b+c)$をすべて挙げよ。
(3) (2)で求めた$(a,b,c)$について、
頂点$A,B,C$と向かい合う辺の長さがそれぞれ
$a,b,c$で与えられる$\triangle ABC$を考える。
このようなすべての$\triangle ABC$について
$\cos \angle ACB$を求めよ。
$2025$年北海道大学文系過去問題
この動画を見る
$\boxed{2}$
整数$a,b,c$は条件
$2\leqq a \lt b \lt c \leqq 6$を満たすとする。
(1)不等式$a+b\gt c$を満たすような
$(a+b+c)$をすべて挙げよ。
(2)不等式$a^2+b^2\geqq c^2$を満たすような
$(a+b+c)$をすべて挙げよ。
(3) (2)で求めた$(a,b,c)$について、
頂点$A,B,C$と向かい合う辺の長さがそれぞれ
$a,b,c$で与えられる$\triangle ABC$を考える。
このようなすべての$\triangle ABC$について
$\cos \angle ACB$を求めよ。
$2025$年北海道大学文系過去問題
【数Ⅰ】【図形と計量】測量の応用2 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
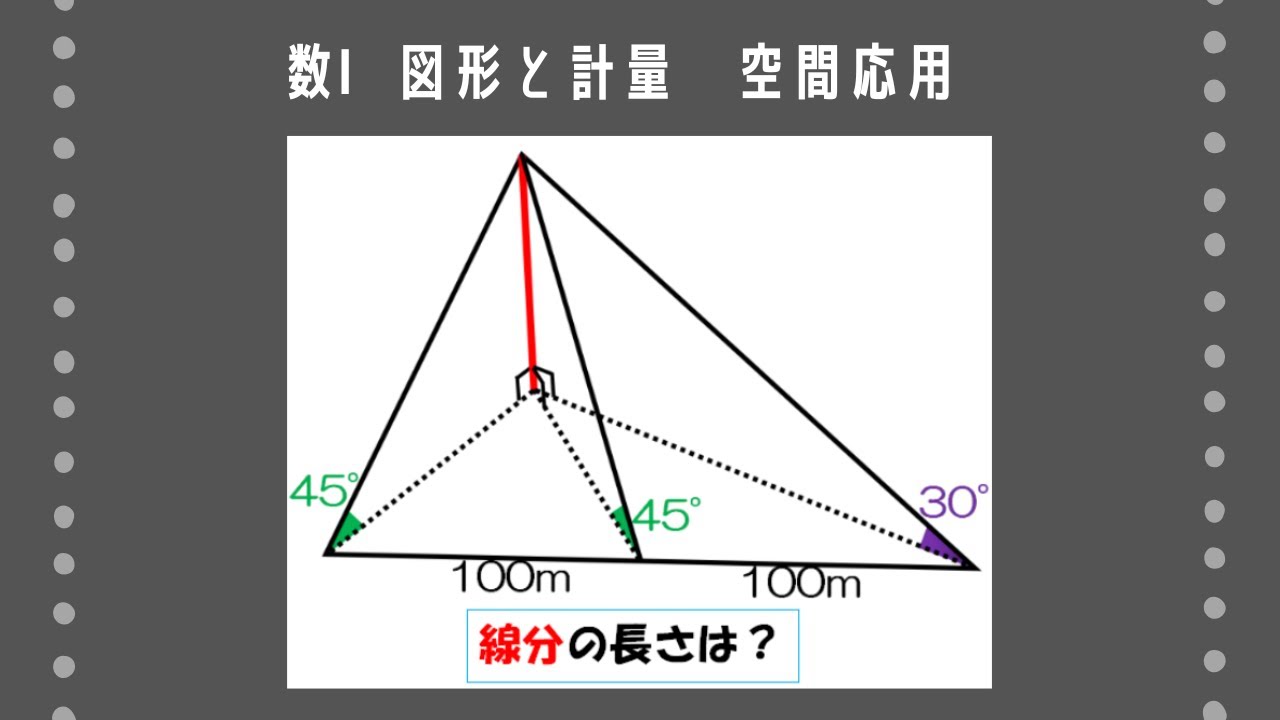
右の図のように1つの直線上にならぶ水平面上の3点A、B、Cから山頂Dの仰角を測ると、それぞれ45°、45°、30°であったという。AB=100m、BC=100mであるとき、山の高さDHを求めよ。
この動画を見る
右の図のように1つの直線上にならぶ水平面上の3点A、B、Cから山頂Dの仰角を測ると、それぞれ45°、45°、30°であったという。AB=100m、BC=100mであるとき、山の高さDHを求めよ。
【数Ⅰ】【図形と計量】測量の応用1 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
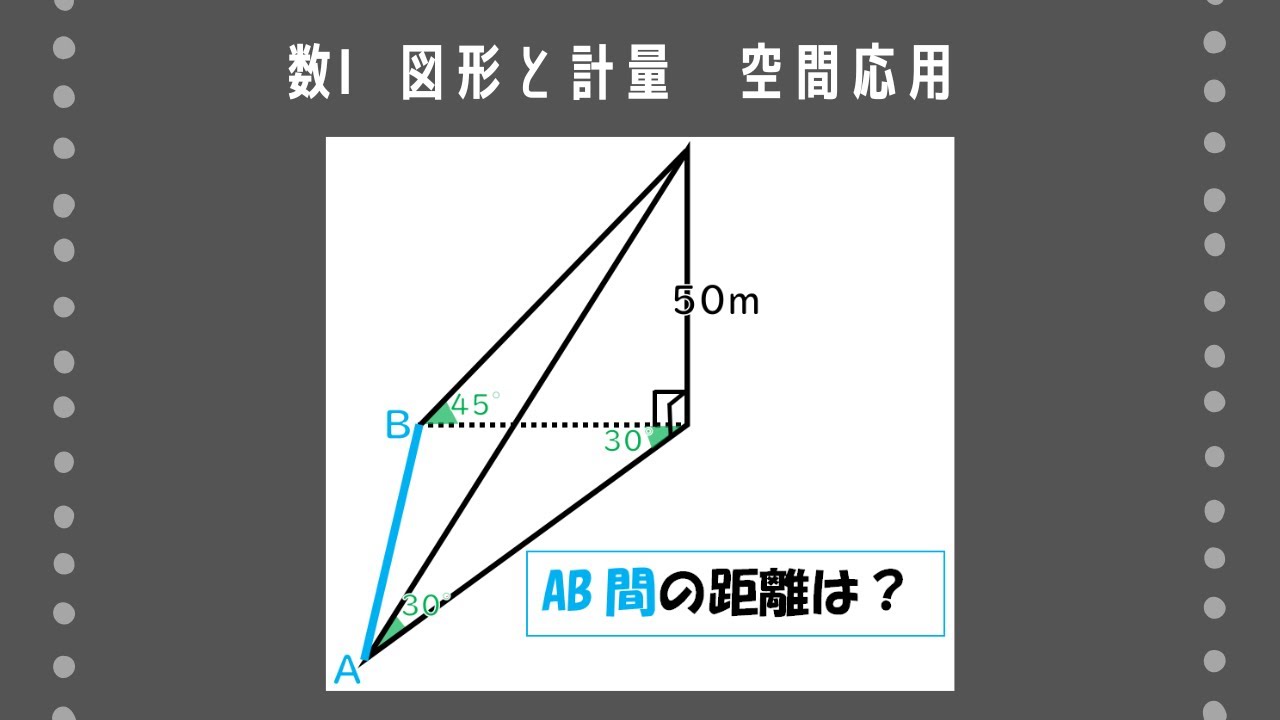
高さ50mの塔が立っている地点Hと同じ標高の地点Aから、塔の先端Pを見たところ、仰角が30°であった。また、Hと同じ標高の地点BからPを見たところ、仰角が45°で、∠BHA=30°であった。2地点A、B間の距離を求めよ。
この動画を見る
高さ50mの塔が立っている地点Hと同じ標高の地点Aから、塔の先端Pを見たところ、仰角が30°であった。また、Hと同じ標高の地点BからPを見たところ、仰角が45°で、∠BHA=30°であった。2地点A、B間の距離を求めよ。
【数Ⅰ】【図形と計量】球2 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
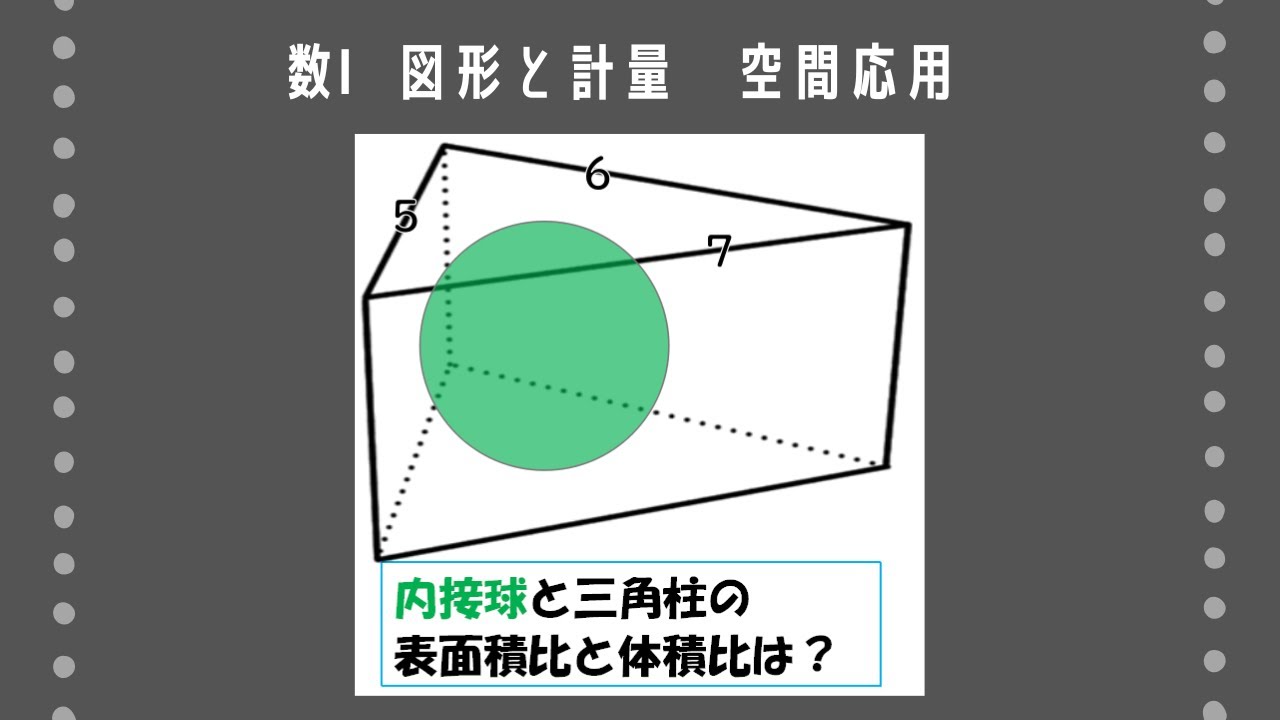
右の図のように、3辺の長さが5、6、7である三角形を底面とする三角柱に、三角柱の高さと同じ直径の球が内接している。
(1)球の表面積と体積を求めよ。
(2)三角柱の表面積と体積を求めよ。
(3)球と三角柱の表面積の比を求めよ。
(4)球と三角柱の体積比は、球と三角柱の表面積の比に等しいことを示せ。
※図は動画内参照
この動画を見る
右の図のように、3辺の長さが5、6、7である三角形を底面とする三角柱に、三角柱の高さと同じ直径の球が内接している。
(1)球の表面積と体積を求めよ。
(2)三角柱の表面積と体積を求めよ。
(3)球と三角柱の表面積の比を求めよ。
(4)球と三角柱の体積比は、球と三角柱の表面積の比に等しいことを示せ。
※図は動画内参照
【数Ⅰ】【図形と計量】球1 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
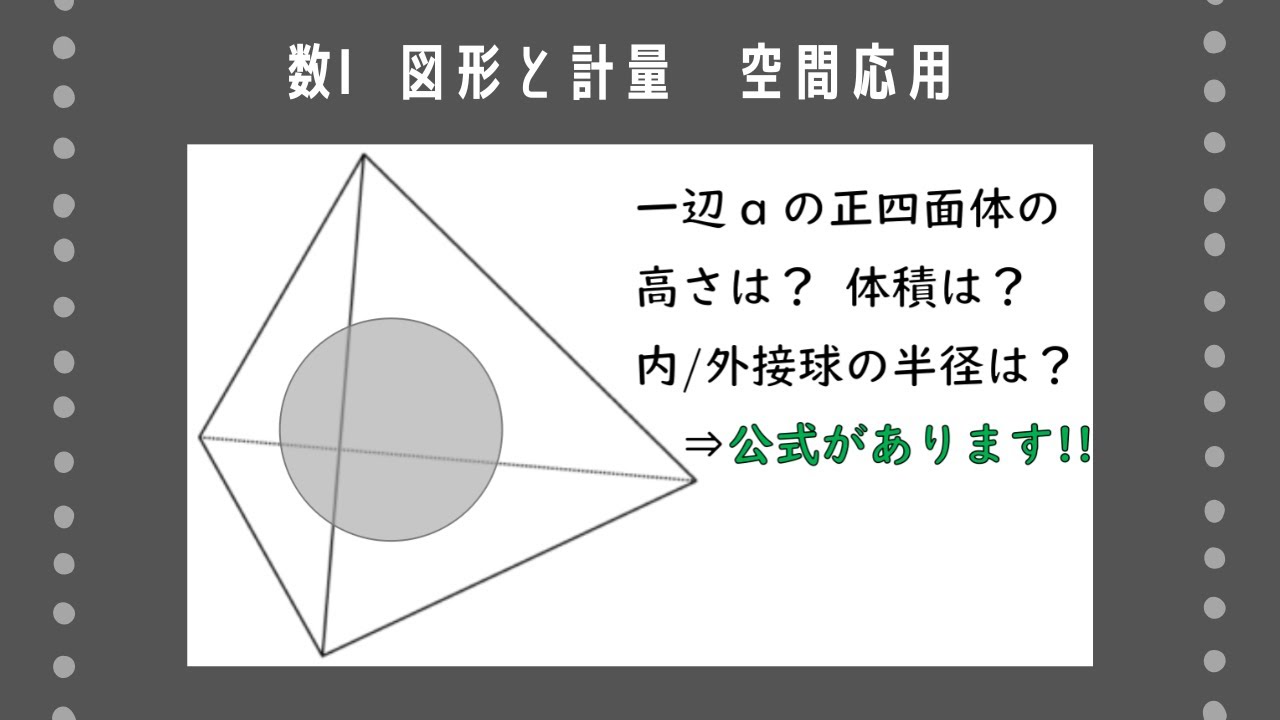
1辺の長さが3の正四面体ABCDに内接する球の中心をOとする。次の問いに答えよ。
(1)四面体OBCDの体積$V$を求めよ。
(2)球の半径$r$、表面積、体積を求めよ。
この動画を見る
1辺の長さが3の正四面体ABCDに内接する球の中心をOとする。次の問いに答えよ。
(1)四面体OBCDの体積$V$を求めよ。
(2)球の半径$r$、表面積、体積を求めよ。
【数Ⅰ】【図形と計量】空間の応用2 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
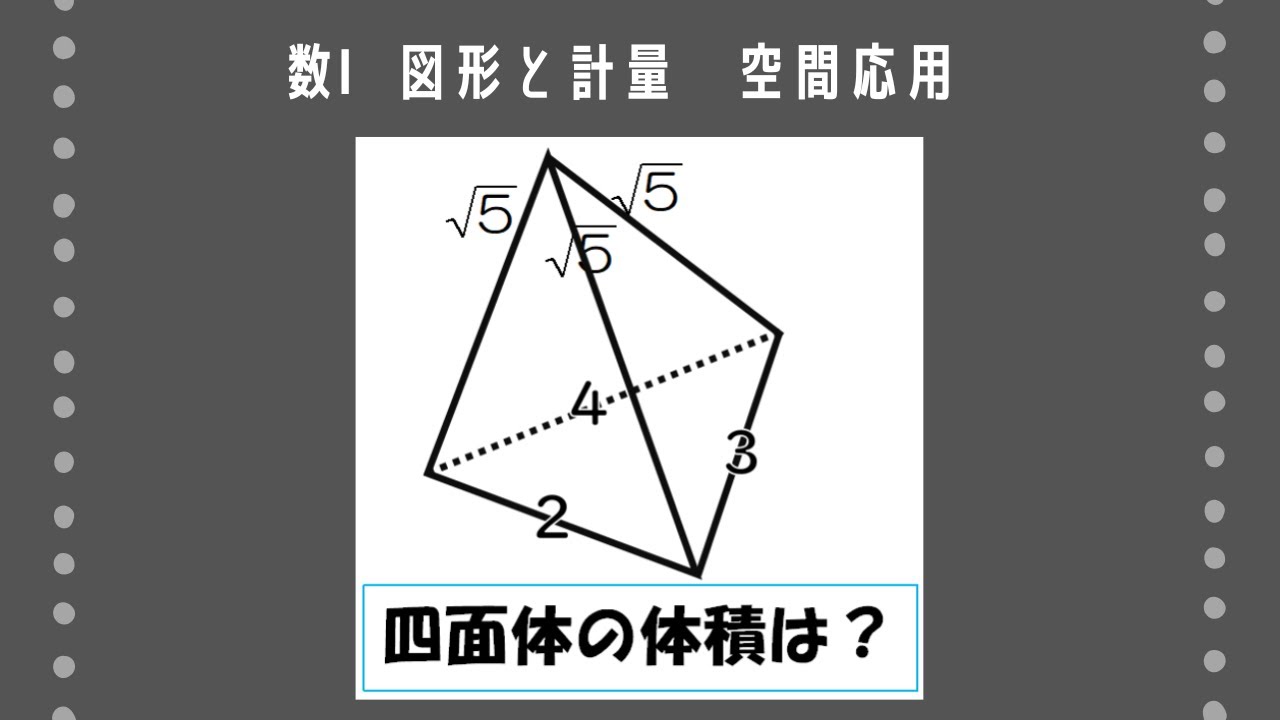
$\rm PA=PB=PC=\sqrt5,AB=3,BC=3,CA=4$である三角錐PABCの体積を求めよ。
この動画を見る
$\rm PA=PB=PC=\sqrt5,AB=3,BC=3,CA=4$である三角錐PABCの体積を求めよ。
【数Ⅰ】【図形と計量】空間の応用1 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
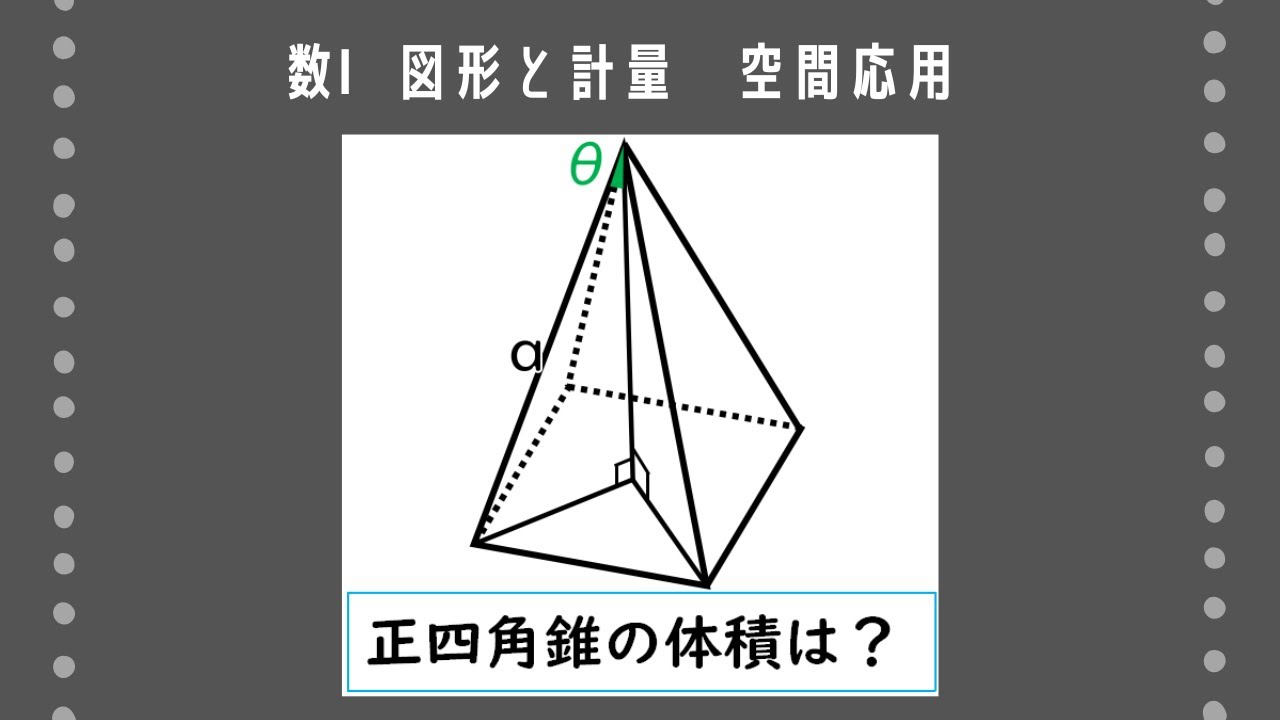
図のような正四角錐$\rm PABCD$において、頂点$\rm P$から正方形$\rm ABCD$に下ろした垂線を$\rm PH$とする。$\rm PA=a,\angle APH=\theta$であるとき、正四角錐の体積を求めよ。
この動画を見る
図のような正四角錐$\rm PABCD$において、頂点$\rm P$から正方形$\rm ABCD$に下ろした垂線を$\rm PH$とする。$\rm PA=a,\angle APH=\theta$であるとき、正四角錐の体積を求めよ。
【数Ⅰ】【図形と計量】空間の基本2 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
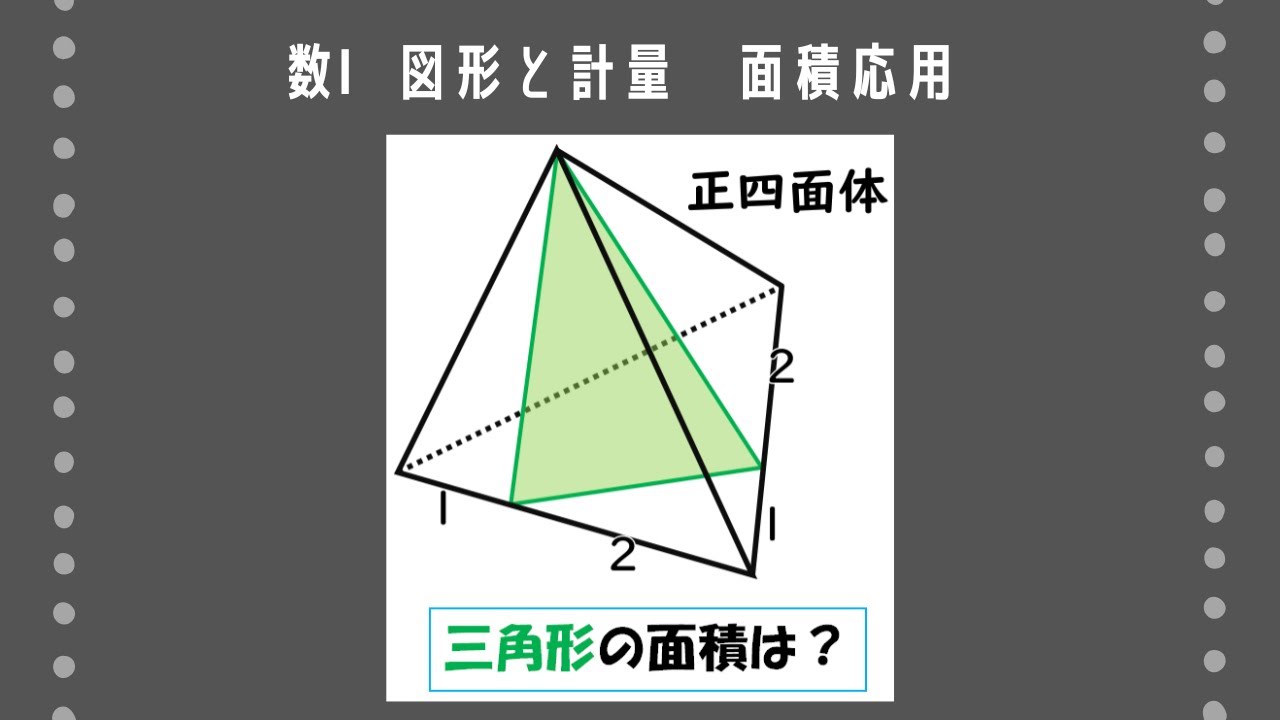
1辺の長さが3の正四面体$\rm ABCD$において、辺$\rm BC,CD$を$1:2$に分ける点を、それぞれ$\rm P,Q$とする。このとき、次のものを求めよ。
(1)$\rm AP,AQ,PQ$の長さ (2)$\cos \angle \rm PAQ$の値 (3)$\rm \triangle APQ$の面積
この動画を見る
1辺の長さが3の正四面体$\rm ABCD$において、辺$\rm BC,CD$を$1:2$に分ける点を、それぞれ$\rm P,Q$とする。このとき、次のものを求めよ。
(1)$\rm AP,AQ,PQ$の長さ (2)$\cos \angle \rm PAQ$の値 (3)$\rm \triangle APQ$の面積
【数Ⅰ】【図形と計量】空間の基本3 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
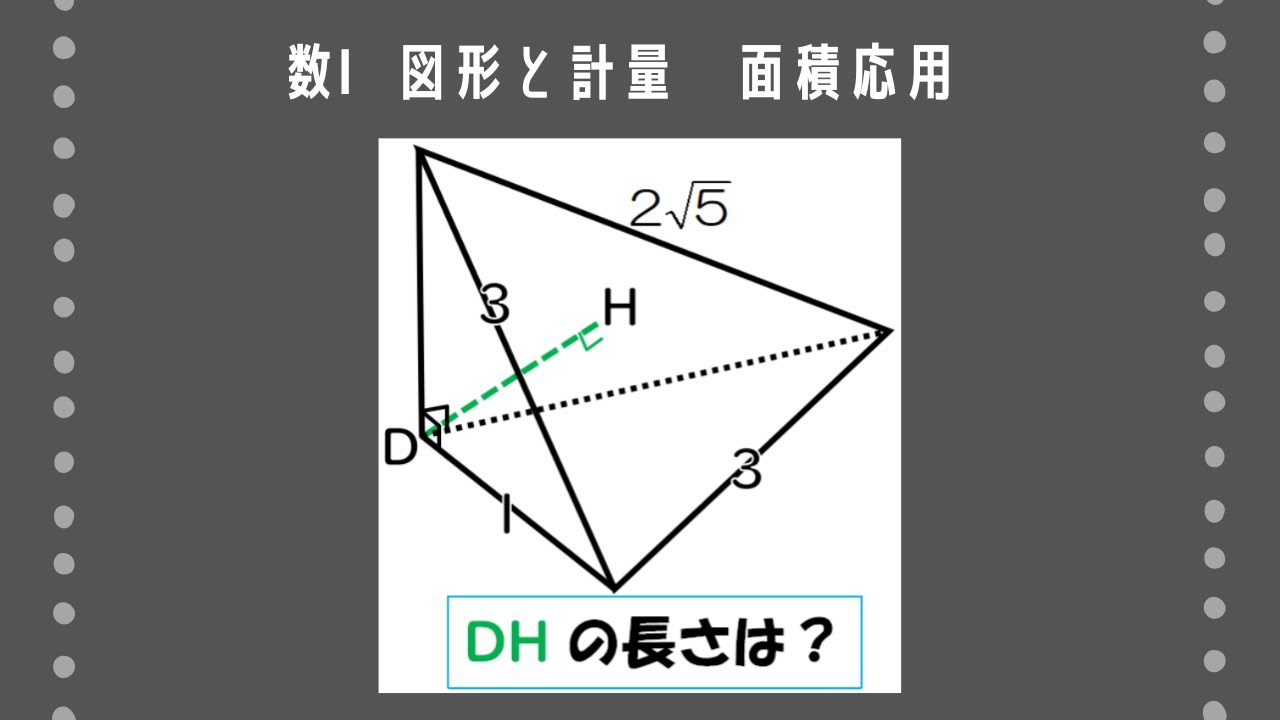
四面体$\rm ABCD$において、$\rm AB=BC=3,CA=2\sqrt5,BD=1,\angle ADB=\angle ADC=90^{\circ}$であるとき、次のものを求めよ。
(1)$\rm CD$の長さ (2)四面体$\rm ABCD$の体積 (3)$\triangle \rm ABC$の面積 (4)頂点$\rm D$から平面
この動画を見る
四面体$\rm ABCD$において、$\rm AB=BC=3,CA=2\sqrt5,BD=1,\angle ADB=\angle ADC=90^{\circ}$であるとき、次のものを求めよ。
(1)$\rm CD$の長さ (2)四面体$\rm ABCD$の体積 (3)$\triangle \rm ABC$の面積 (4)頂点$\rm D$から平面
【数Ⅰ】【図形と計量】空間の基本1 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
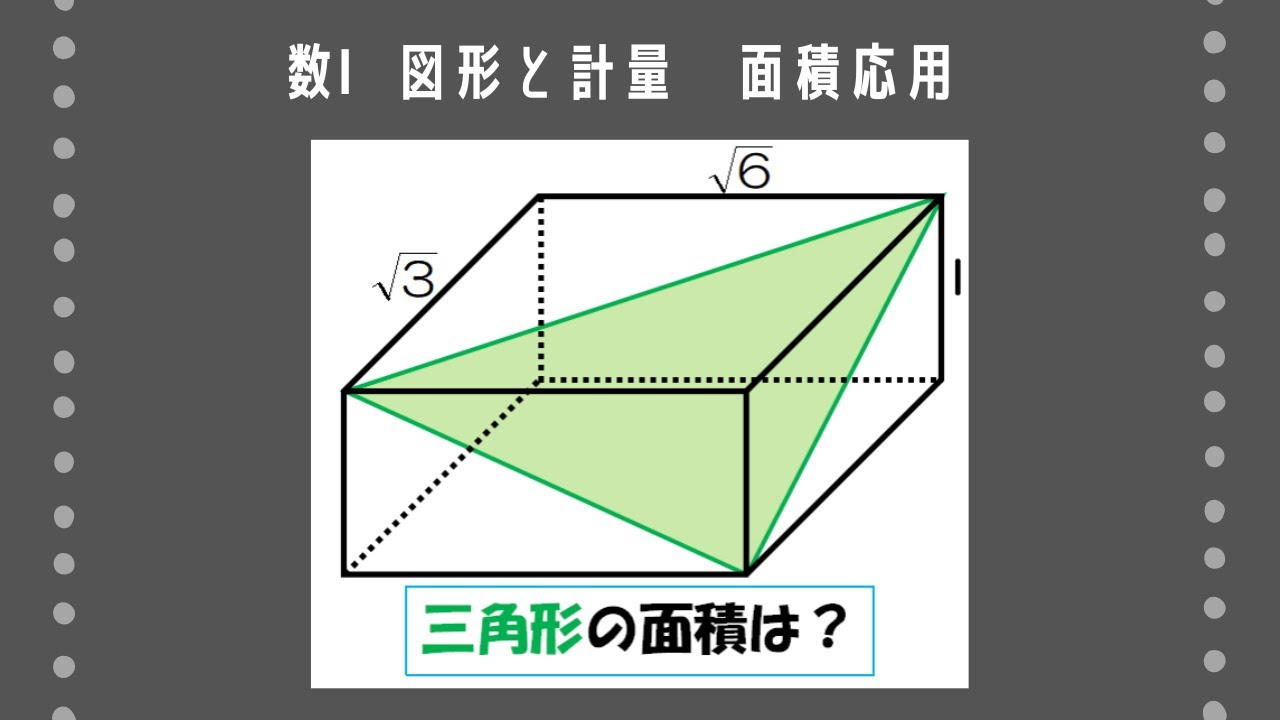
右の図のような$\rm AB=\sqrt6,AD=\sqrt3,AE=1$である直方体$\rm ABCD-EFGH$がある。このとき、次のものを求めよ。
(1)$\rm\angle ACF$の大きさ
(2)$\rm \triangle ACF$の面積
この動画を見る
右の図のような$\rm AB=\sqrt6,AD=\sqrt3,AE=1$である直方体$\rm ABCD-EFGH$がある。このとき、次のものを求めよ。
(1)$\rm\angle ACF$の大きさ
(2)$\rm \triangle ACF$の面積
【数Ⅰ】【図形と計量】面積応用10 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
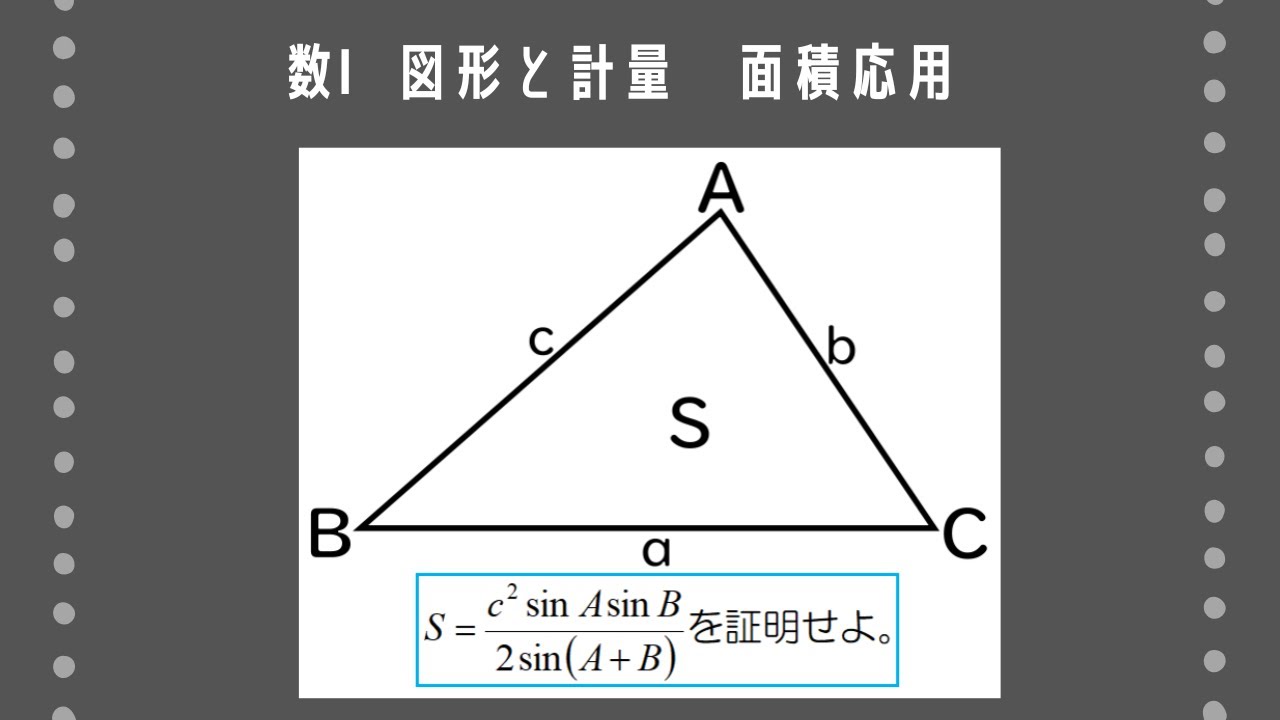
1辺$c$と2つの角$\rm A,B$が与えられた$rm\triangle ABC$の面積を$S$とするとき、次の問いに答えよ。
(1)$a$を$c,\rm A,B$で表せ。 (2)$S=\dfrac{c^2\rm\sin A\sin B}{2\sin\rm(A+B)}$を証明せよ。
この動画を見る
1辺$c$と2つの角$\rm A,B$が与えられた$rm\triangle ABC$の面積を$S$とするとき、次の問いに答えよ。
(1)$a$を$c,\rm A,B$で表せ。 (2)$S=\dfrac{c^2\rm\sin A\sin B}{2\sin\rm(A+B)}$を証明せよ。
【数Ⅰ】【図形と計量】面積応用9 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
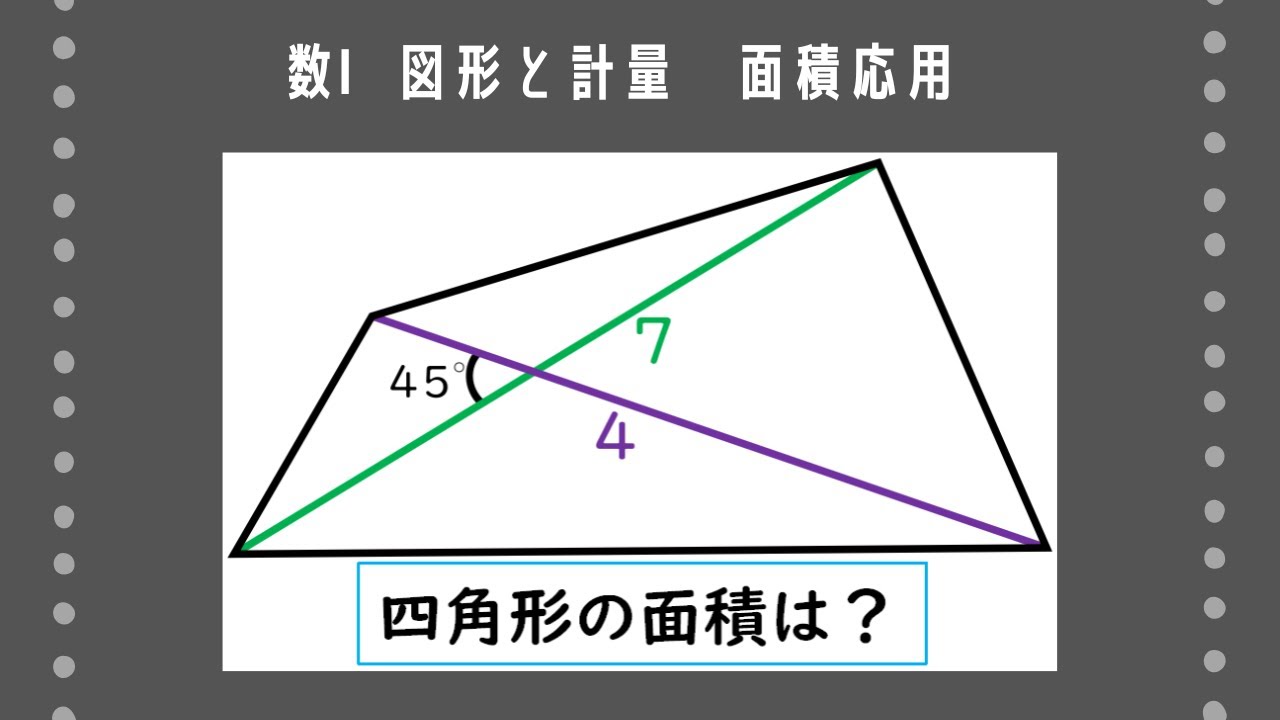
四角形$\rm ABCD$の2つの対角線$\rm AC,BD$の交点を$\rm O$とする。$\rm AC=4,BD=7,\angle AOB=45^{\circ}$であるとき、四角形$\rm ABCD$の面積$S$を求めよ。
この動画を見る
四角形$\rm ABCD$の2つの対角線$\rm AC,BD$の交点を$\rm O$とする。$\rm AC=4,BD=7,\angle AOB=45^{\circ}$であるとき、四角形$\rm ABCD$の面積$S$を求めよ。
【数Ⅰ】【図形と計量】面積応用8 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
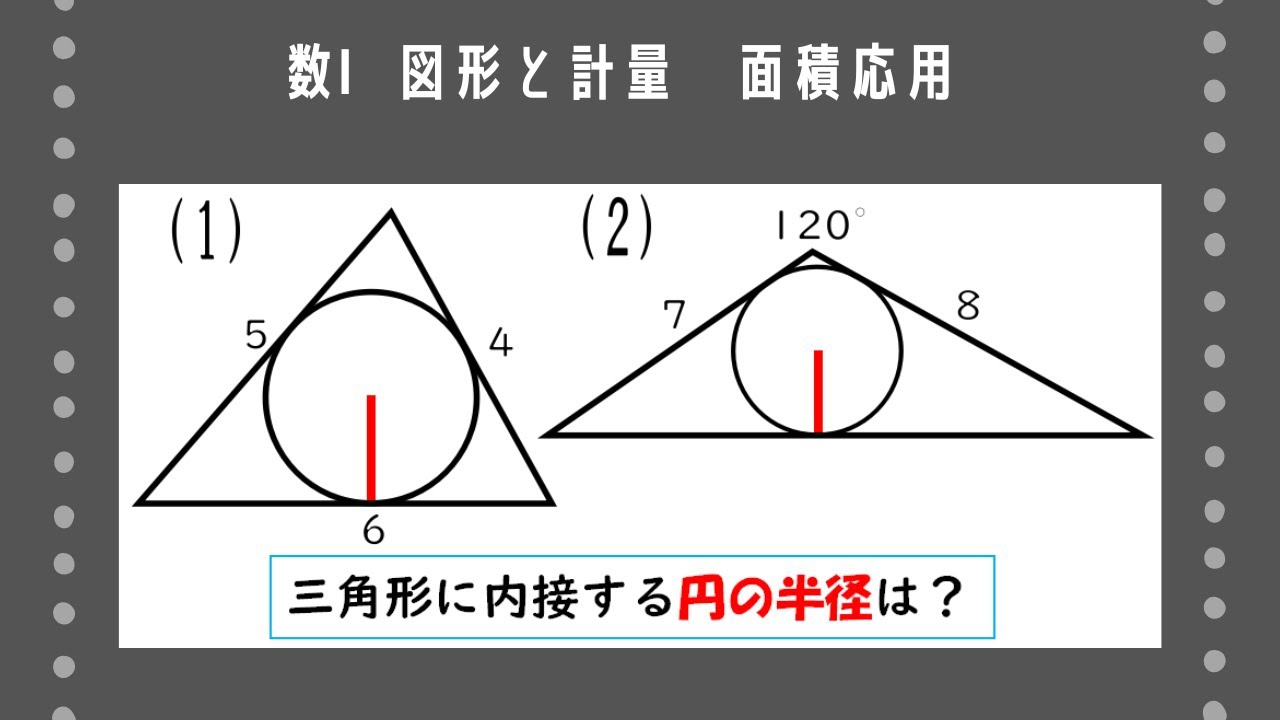
次のような$\rm \triangle ABC$に内接する円の半径$r$を求めよ。
(1)$a=4,b=5,c=6$ (2)${\rm A=120^{\circ}},b=7,c=8$
この動画を見る
次のような$\rm \triangle ABC$に内接する円の半径$r$を求めよ。
(1)$a=4,b=5,c=6$ (2)${\rm A=120^{\circ}},b=7,c=8$
【数Ⅰ】【図形と計量】面積応用3 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
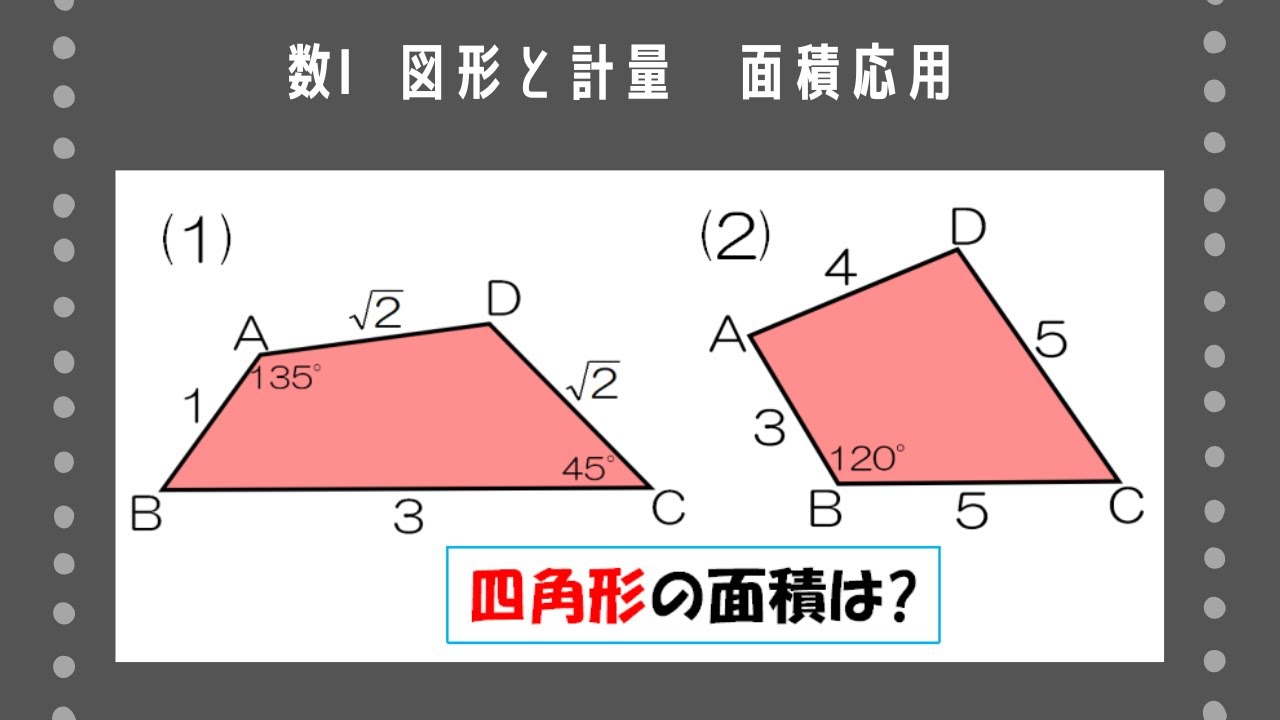
次のような四角形ABCDの面積を求めよ。
(1)∠A=135°、∠C=45°、AB=1、BC=3、CD=$\sqrt{2}$、DA=$\sqrt{2}$
(2)∠B=120°、AB=3、BC=5、CD=5、DA=4
この動画を見る
次のような四角形ABCDの面積を求めよ。
(1)∠A=135°、∠C=45°、AB=1、BC=3、CD=$\sqrt{2}$、DA=$\sqrt{2}$
(2)∠B=120°、AB=3、BC=5、CD=5、DA=4
【数Ⅰ】【図形と計量】面積応用2 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
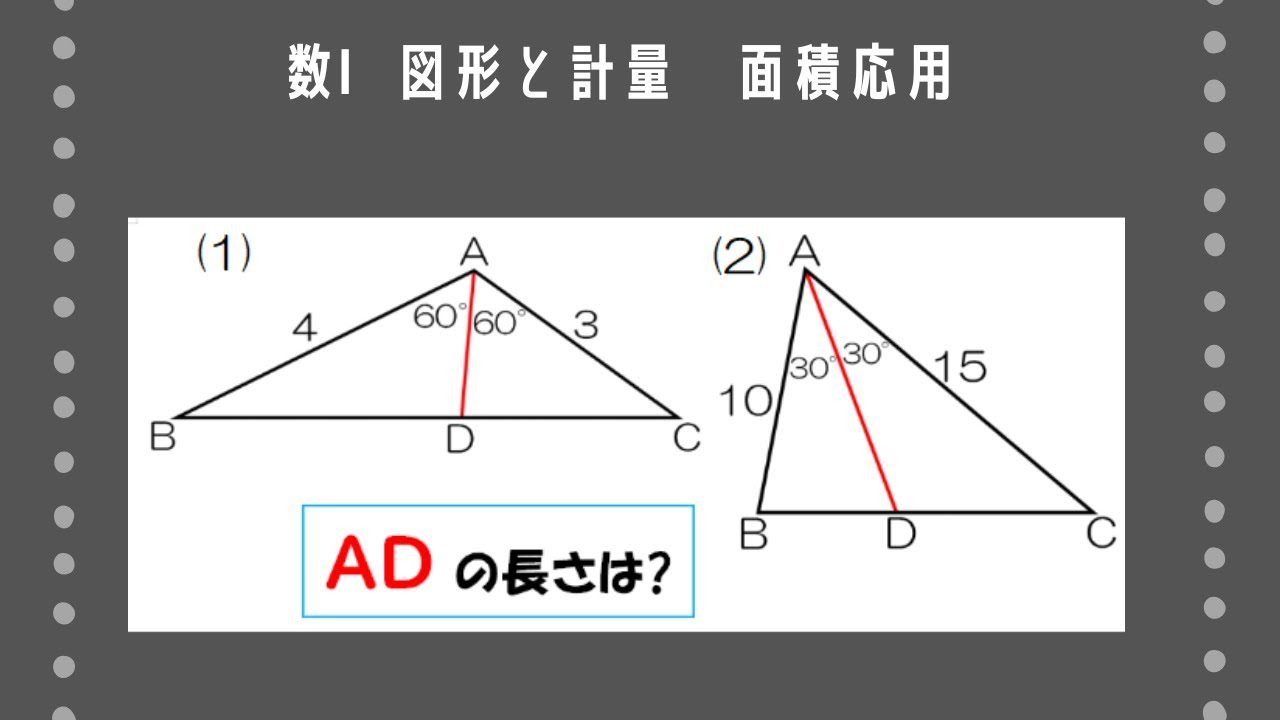
次のような△ABCについて、∠Aの二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
(1)AB=4、AC=3、A=120°
(2)AB=10、AC=15、A=60°
この動画を見る
次のような△ABCについて、∠Aの二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
(1)AB=4、AC=3、A=120°
(2)AB=10、AC=15、A=60°
【数Ⅰ】【図形と計量】面積応用7 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
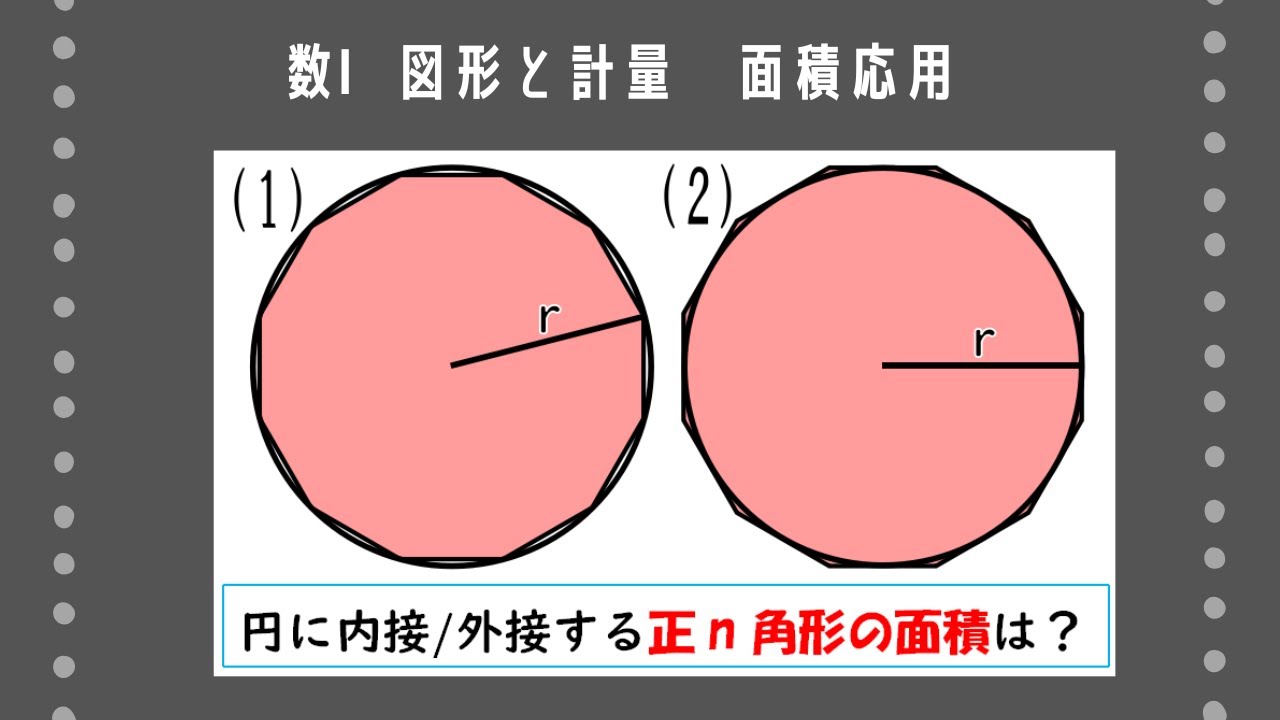
半径$r$の円に内接する正$n$角形の面積、および外接する正$n$角形の面積を、それぞれ$r$と$n$を用いて求めよ。
この動画を見る
半径$r$の円に内接する正$n$角形の面積、および外接する正$n$角形の面積を、それぞれ$r$と$n$を用いて求めよ。
【数Ⅰ】【図形と計量】面積応用5 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
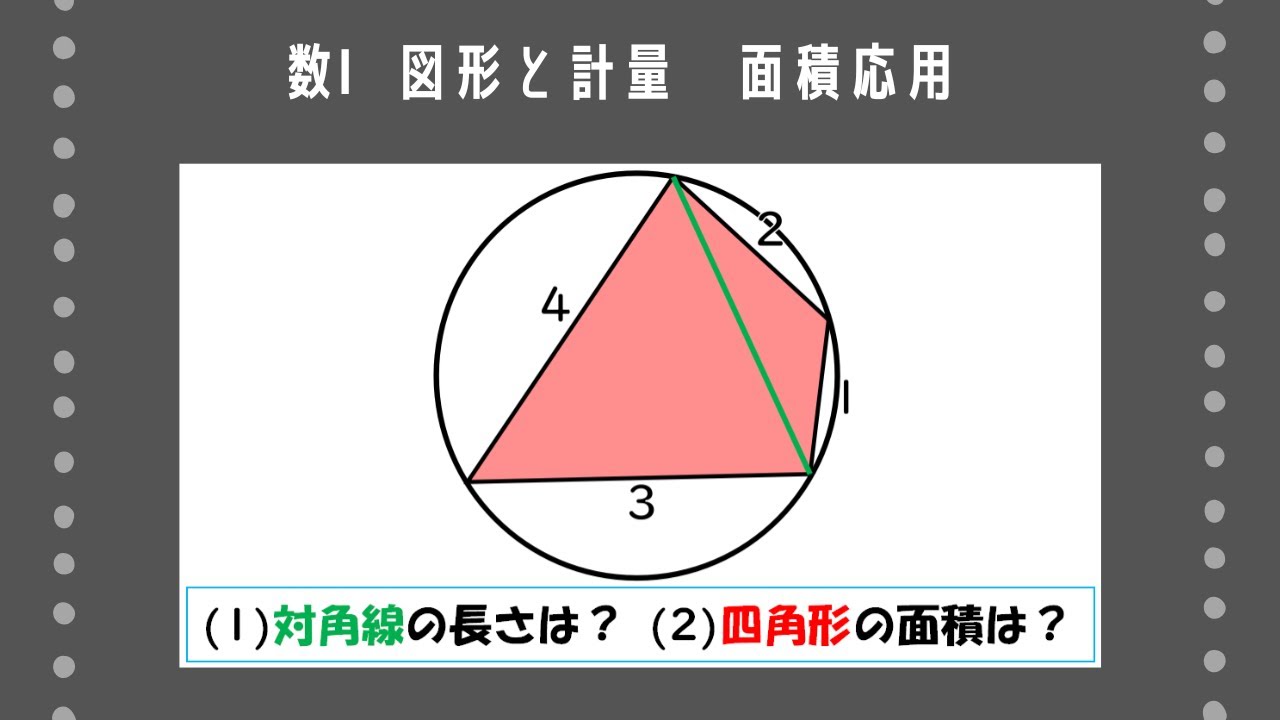
円に内接する四角形$\rm ABCD$において、$\rm AB=4,BC=3,CD=1,DA=2$とするとき、次のものを求めよ。
(1)対角線$\rm AC$の長さ
(2)四角形$\rm ABCD$の面積
この動画を見る
円に内接する四角形$\rm ABCD$において、$\rm AB=4,BC=3,CD=1,DA=2$とするとき、次のものを求めよ。
(1)対角線$\rm AC$の長さ
(2)四角形$\rm ABCD$の面積
【数Ⅰ】【図形と計量】面積応用4 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
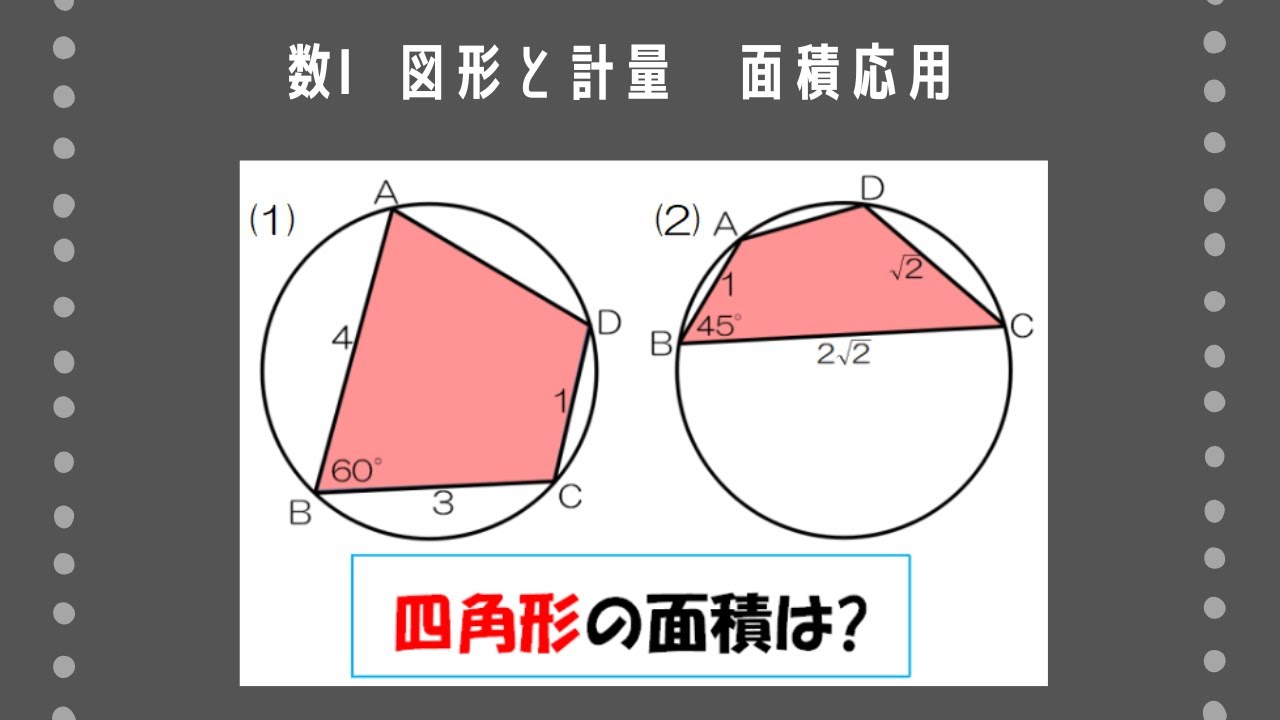
次のような四角形$\rm ABCD$の面積を求めよ。
(1)円に内接し、$\rm AB=4,BC=3,CD=1,\angle B=60^{\circ}$
(2)円に内接し、$\rm AB=1,BC=2\sqrt2,CD=\sqrt2,\angle B=45^{\circ}$
この動画を見る
次のような四角形$\rm ABCD$の面積を求めよ。
(1)円に内接し、$\rm AB=4,BC=3,CD=1,\angle B=60^{\circ}$
(2)円に内接し、$\rm AB=1,BC=2\sqrt2,CD=\sqrt2,\angle B=45^{\circ}$
【数Ⅰ】【図形と計量】面積応用6 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
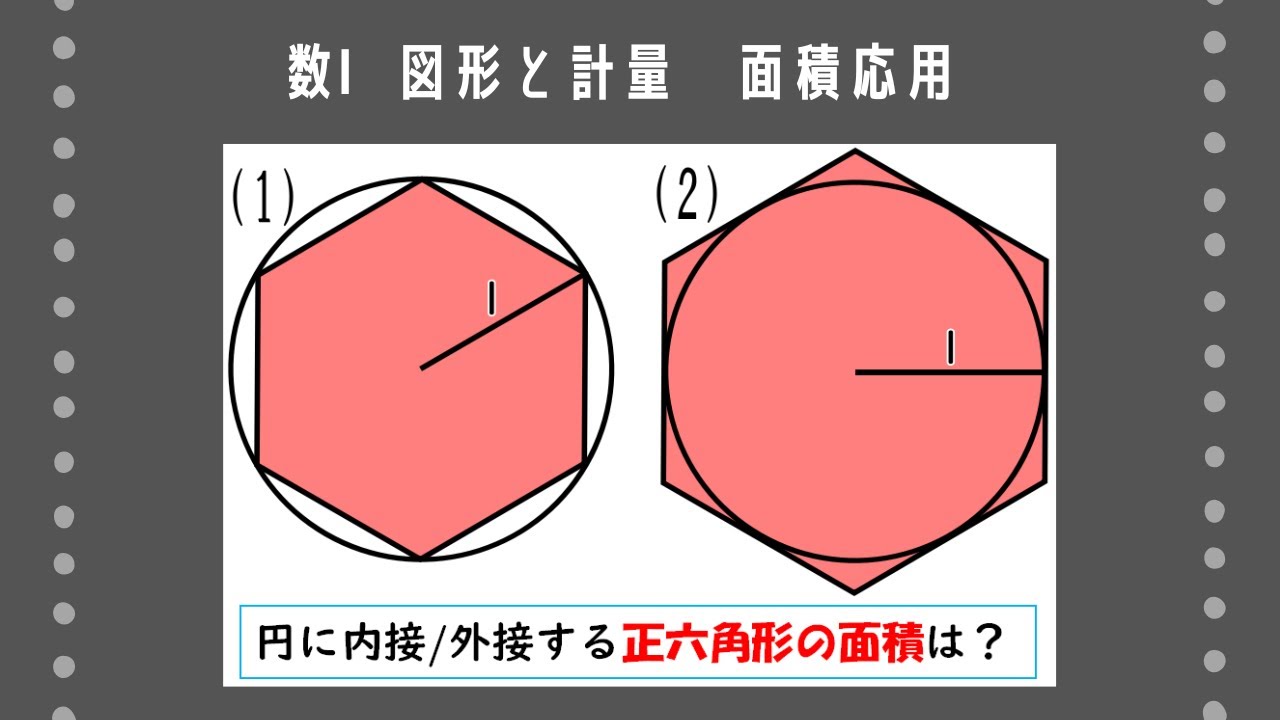
(1)半径1の円に内接する正六角形の面積を求めよ。
(2)半径1の円に外接する正六角形の面積を求めよ。
この動画を見る
(1)半径1の円に内接する正六角形の面積を求めよ。
(2)半径1の円に外接する正六角形の面積を求めよ。
【数Ⅰ】【図形と計量】面積応用1 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
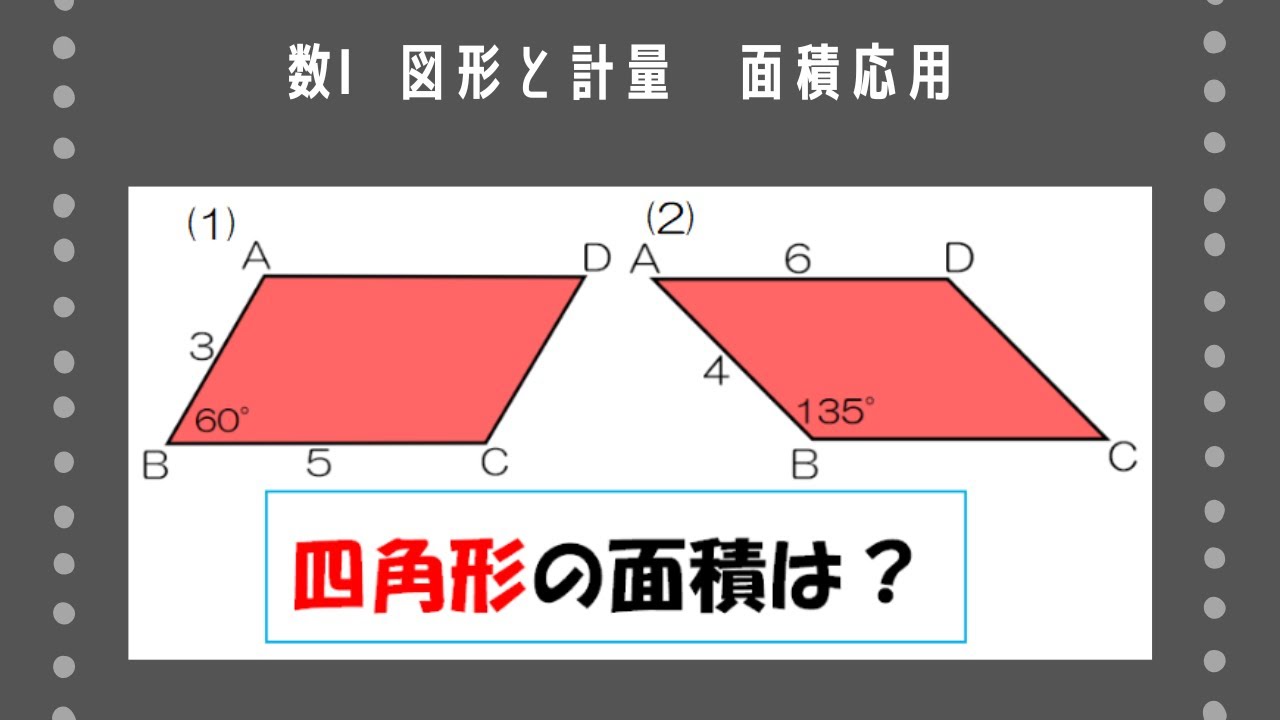
次のような平行四辺形ABCDの面積を求めよ。
(1)AB=3、BC=5、∠ABC=60°
(2)AB=4、AD=6、∠ABC=135°
この動画を見る
次のような平行四辺形ABCDの面積を求めよ。
(1)AB=3、BC=5、∠ABC=60°
(2)AB=4、AD=6、∠ABC=135°
【数Ⅰ】【図形と計量】正弦定理と余弦定理の応用3 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
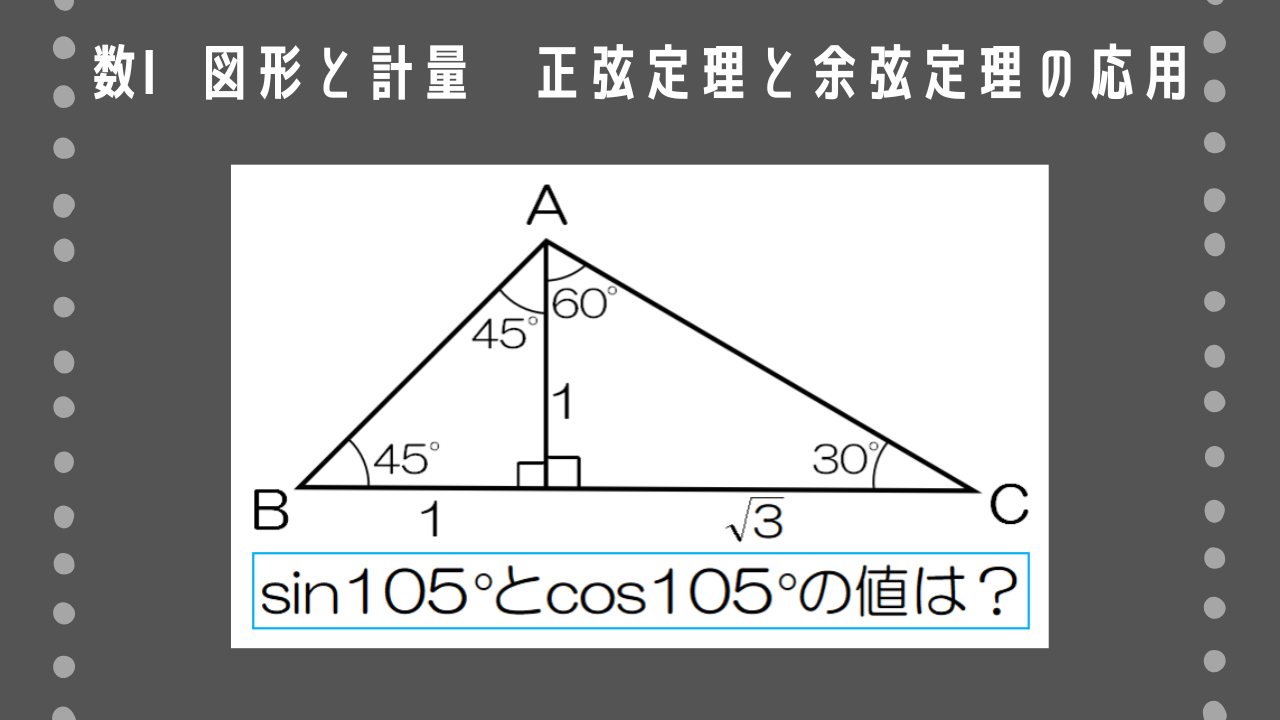
図を利用して、sin105°とcos105°の値を求めよ。
この動画を見る
図を利用して、sin105°とcos105°の値を求めよ。
