 図形と計量
図形と計量
 図形と計量
図形と計量
cosとは何か?から解説!!

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$cos1°+cos2°+cos3°+ \cdots +cos179° = ?$
この動画を見る
$cos1°+cos2°+cos3°+ \cdots +cos179° = ?$
二乗の差は和と差の積

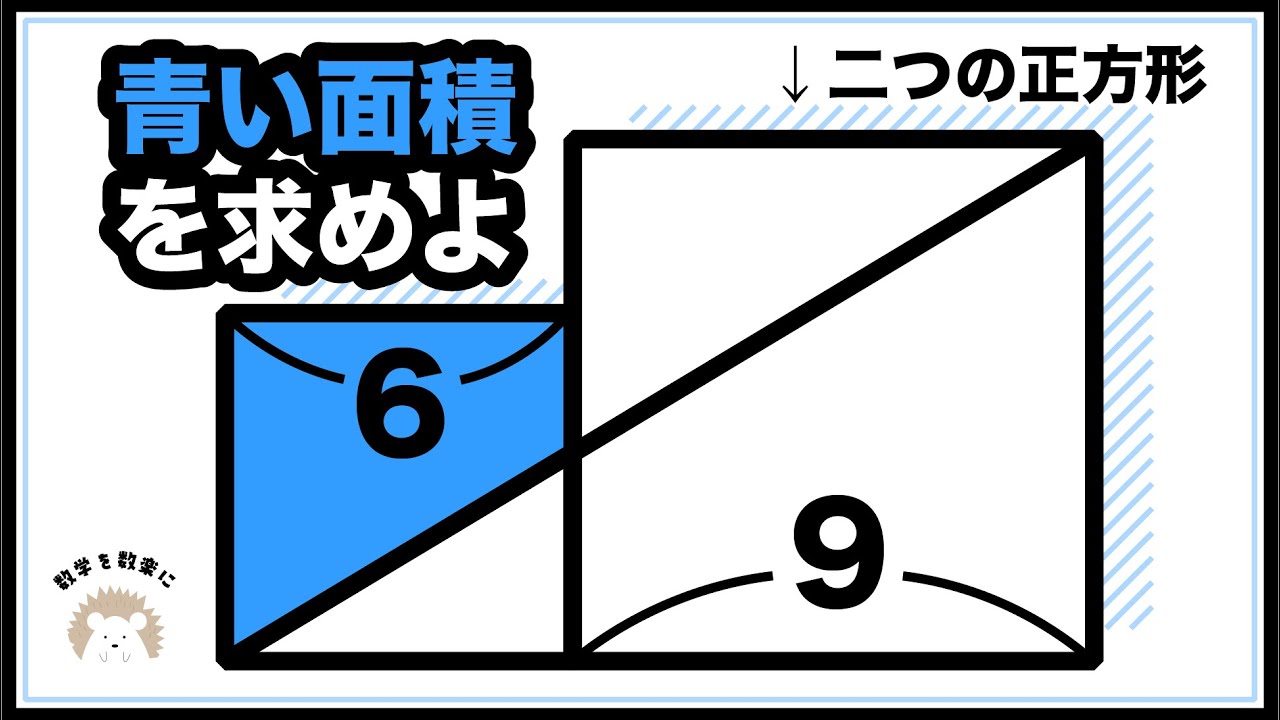
斜線部の面積=❓
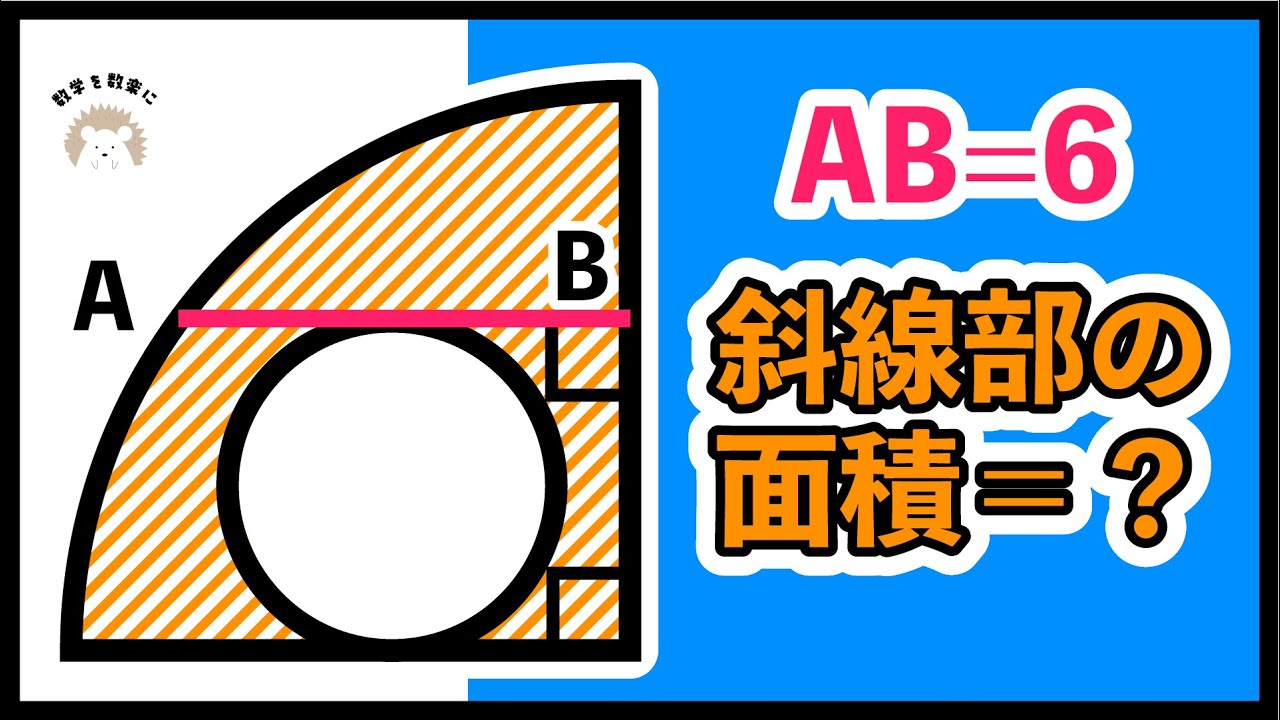
【得意分野にしよう!】図形:興南高等学校~全国入試問題解法
単元:
#数学(中学生)#数Ⅰ#図形と計量#高校入試過去問(数学)#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
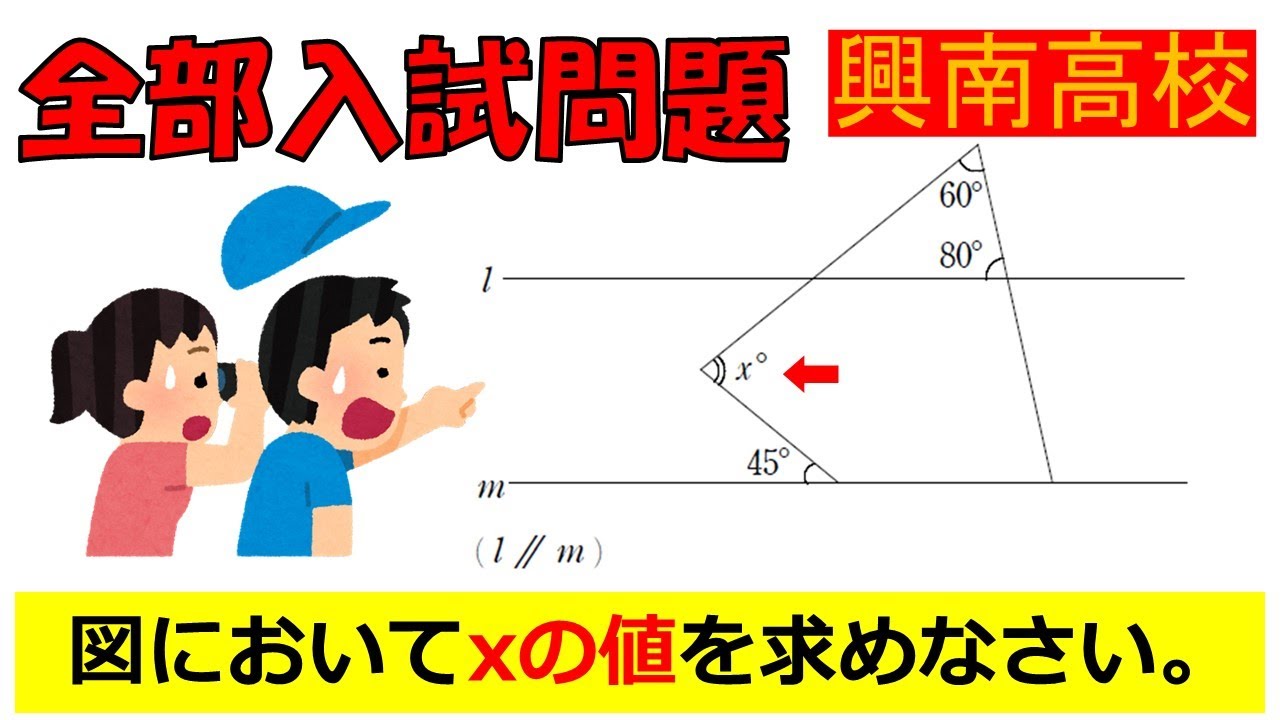
図においてxの値を求めなさい.
興南高等学校過去問
この動画を見る
図においてxの値を求めなさい.
興南高等学校過去問
図形と計量 三角比の変換応用【NI・SHI・NOがていねいに解説】
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
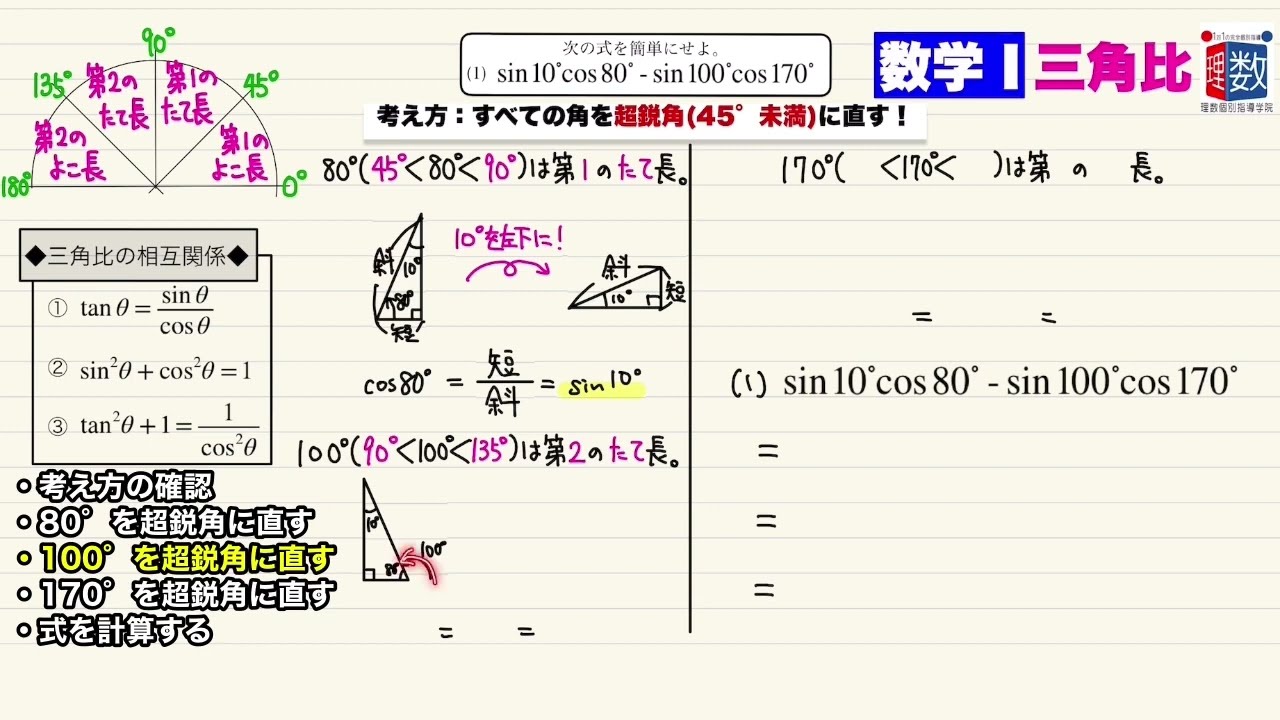
次の式の値を簡単にせよ。
(1) $\sin 10°\cos 80°-\sin 100°\cos 170°$
(2) $\dfrac{1}{1+\sin^220°}-\tan^2110°$
(3) $\sin^2(180°-\theta)+\sin^2(90°-\theta)+\sin^2(90°+\theta)+cos^2(90°-\theta)$
この動画を見る
次の式の値を簡単にせよ。
(1) $\sin 10°\cos 80°-\sin 100°\cos 170°$
(2) $\dfrac{1}{1+\sin^220°}-\tan^2110°$
(3) $\sin^2(180°-\theta)+\sin^2(90°-\theta)+\sin^2(90°+\theta)+cos^2(90°-\theta)$
図形と計量 三角比大小比較【NI・SHI・NOがていねいに解説】

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の三角比の値を,小さい方から順に並べよ。ただし,三角比の表は用いないものとする。
$\cos10°,\sin40°,\cos80°,\sin110°,\sin130°,\sin160°$
この動画を見る
次の三角比の値を,小さい方から順に並べよ。ただし,三角比の表は用いないものとする。
$\cos10°,\sin40°,\cos80°,\sin110°,\sin130°,\sin160°$
産業医科大 三角比の計算

単元:
#数Ⅰ#大学入試過去問(数学)#複素数平面#図形と計量#三角比(三角比・拡張・相互関係・単位円)#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#数C#産業医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\cos\dfrac{2}{7}\pi+\cos\dfrac{4}{7}\pi+\cos\dfrac{8}{7}\pi=?$
$\sin\dfrac{2}{7}\pi+\sin\dfrac{4}{7}\pi+\sin\dfrac{8}{7}\pi=?$
これらを求めよ。
産業医科大過去問
この動画を見る
$\cos\dfrac{2}{7}\pi+\cos\dfrac{4}{7}\pi+\cos\dfrac{8}{7}\pi=?$
$\sin\dfrac{2}{7}\pi+\sin\dfrac{4}{7}\pi+\sin\dfrac{8}{7}\pi=?$
これらを求めよ。
産業医科大過去問
小学生も解ける!!
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
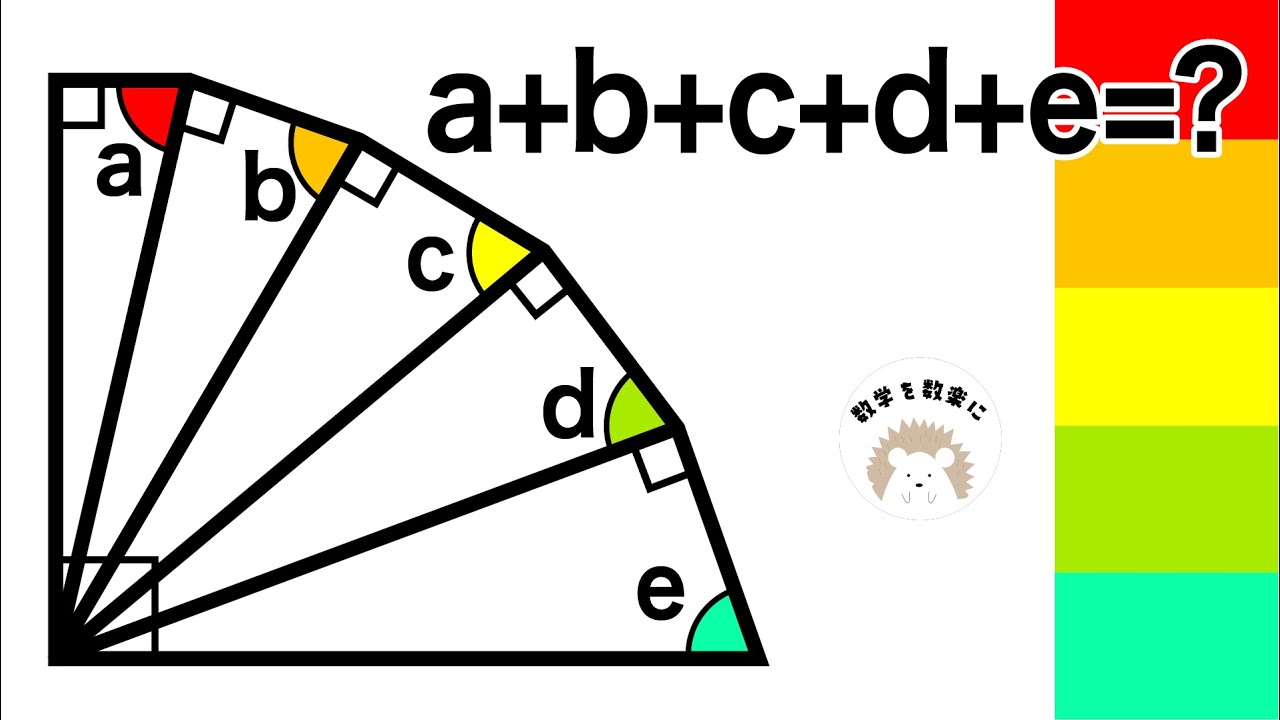
$\angle a + \angle b + \angle c + \angle d + \angle e=?$
この動画を見る
$\angle a + \angle b + \angle c + \angle d + \angle e=?$
図形と計量 2直線のなす角【NI・SHI・NOがていねいに解説】

単元:
#数Ⅰ#図形と計量#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の2直線のなす鋭角$\theta$を求めよ。
(1) $y=-\sqrt{3x}, y=-x$
(2) $y=-\dfrac{1}{\sqrt3}x, y=x$
この動画を見る
次の2直線のなす鋭角$\theta$を求めよ。
(1) $y=-\sqrt{3x}, y=-x$
(2) $y=-\dfrac{1}{\sqrt3}x, y=x$
クイズノックもノックアウト!? 面積比 京都府
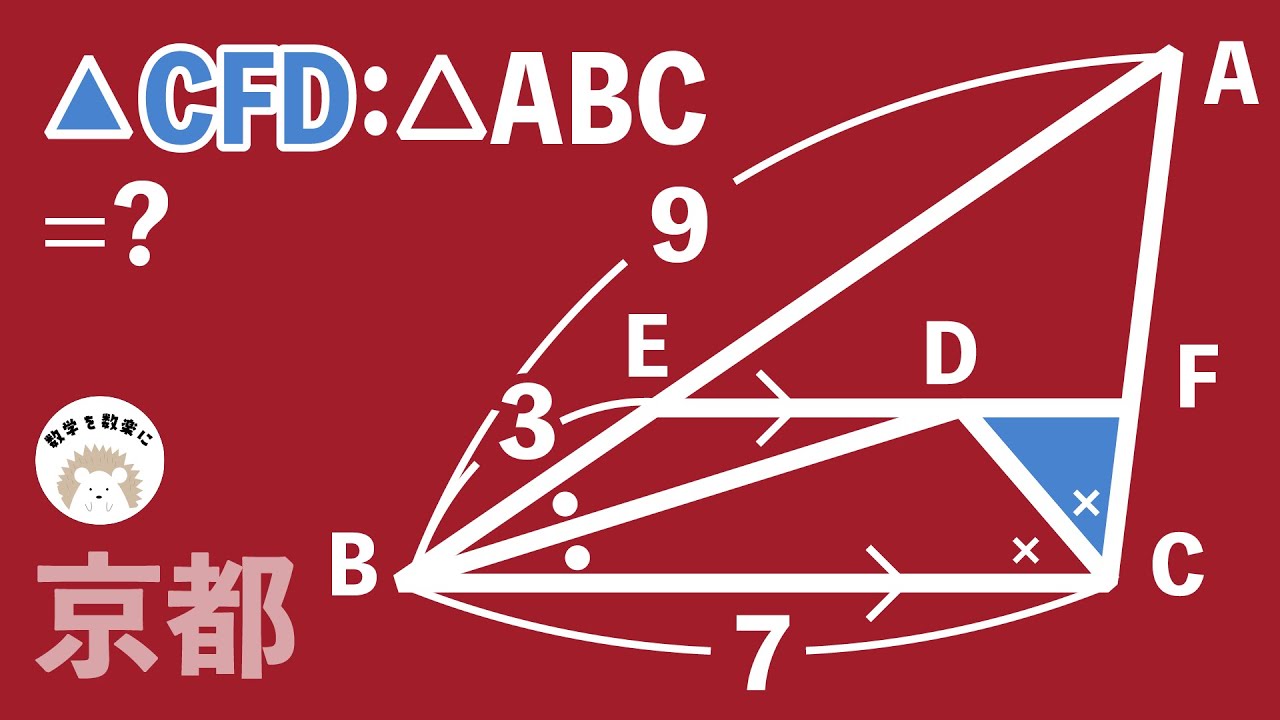
図形と計量 三角比の相互関係の利用2 【NI・SHI・NOがていねいに解説】

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\sin^4\theta-\cos^4\theta$を$\sin\theta$だけを用いた式で表せ。また,$\cos\theta$だけを用いた式で表せ。
この動画を見る
$\sin^4\theta-\cos^4\theta$を$\sin\theta$だけを用いた式で表せ。また,$\cos\theta$だけを用いた式で表せ。
図形と計量 三角比の相互関係の利用【NI・SHI・NOがていねいに解説】
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
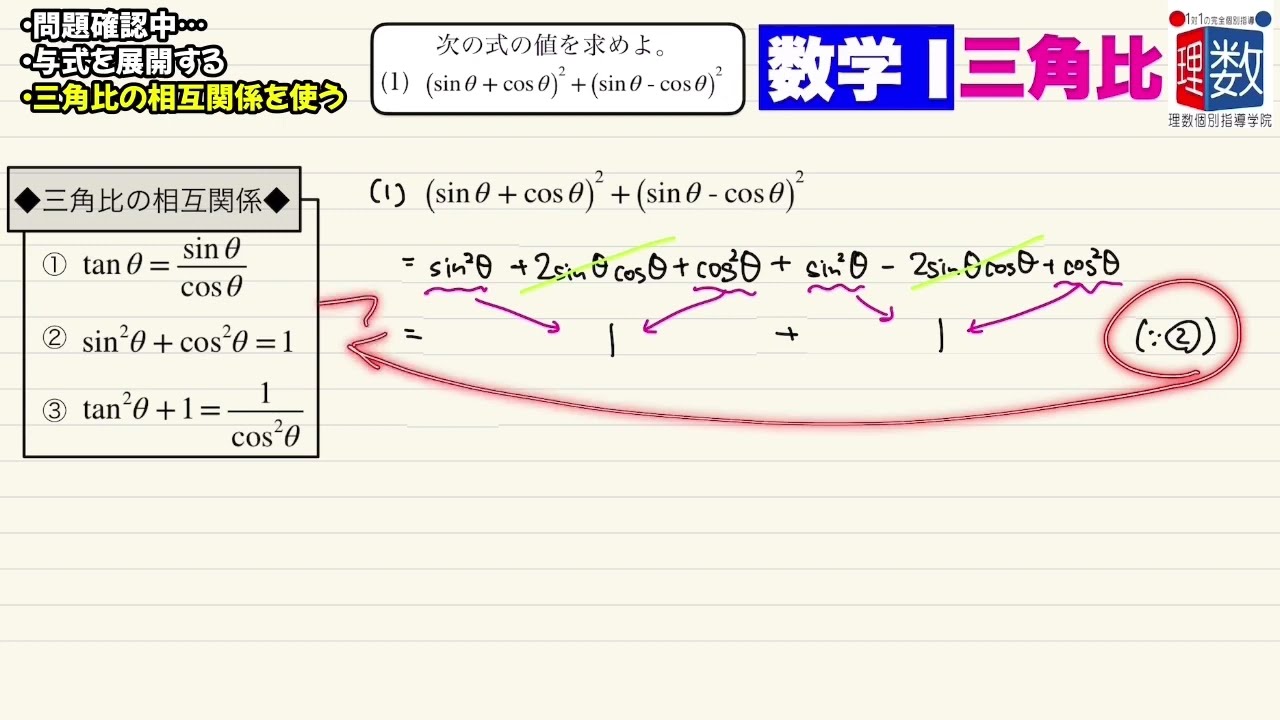
次の式の値を求めよ。
(1)$(\sin\theta+\cos\theta)^2+(\sin\theta-\cos\theta)^2$
(2)$(1-\sin\theta)(1+\sin\theta)-\dfrac{1}{1+\tan^2\theta}$
この動画を見る
次の式の値を求めよ。
(1)$(\sin\theta+\cos\theta)^2+(\sin\theta-\cos\theta)^2$
(2)$(1-\sin\theta)(1+\sin\theta)-\dfrac{1}{1+\tan^2\theta}$
図形と計量 有名角以外を含む三角比計算【NI・SHI・NOがていねいに解説】
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
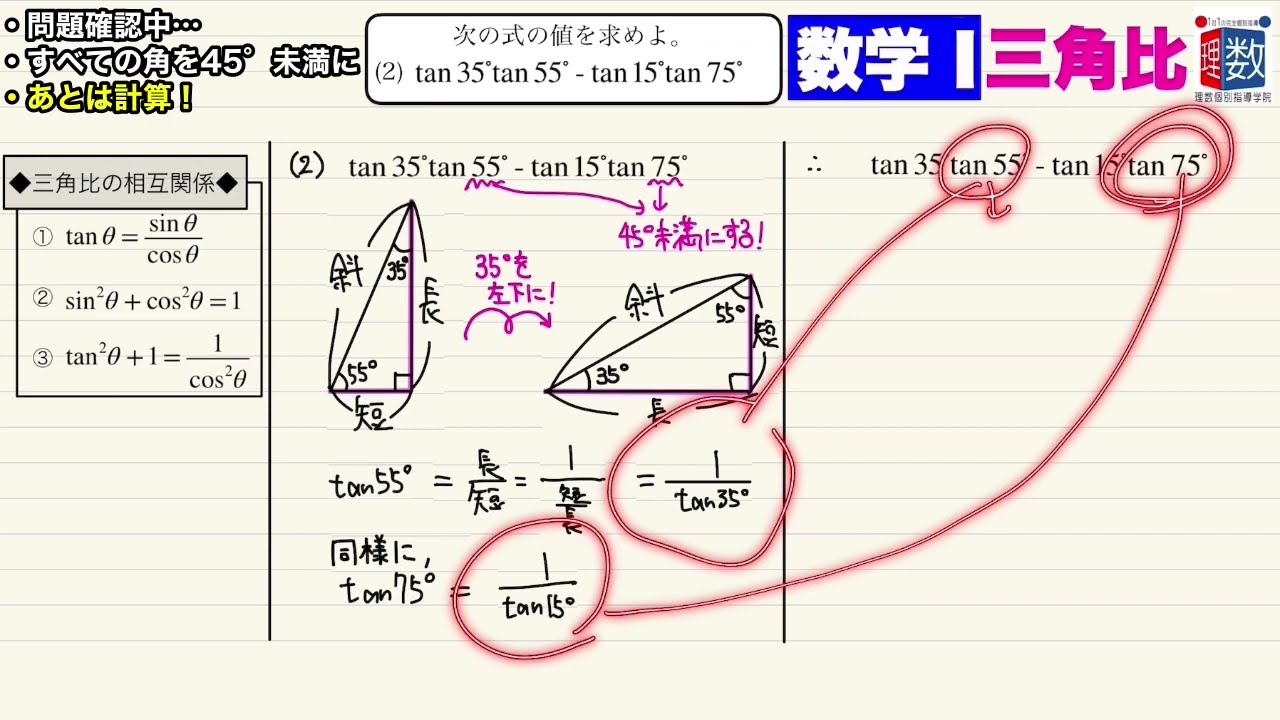
次の式の値を求めよ。
(1) $\sin^240°+\sin^250°$
(2) $\tan35°\tan55°+\tan15°\tan75°$
(3) $(\sin70°+\sin20°)^2-2\tan70°\cos^250°$
この動画を見る
次の式の値を求めよ。
(1) $\sin^240°+\sin^250°$
(2) $\tan35°\tan55°+\tan15°\tan75°$
(3) $(\sin70°+\sin20°)^2-2\tan70°\cos^250°$
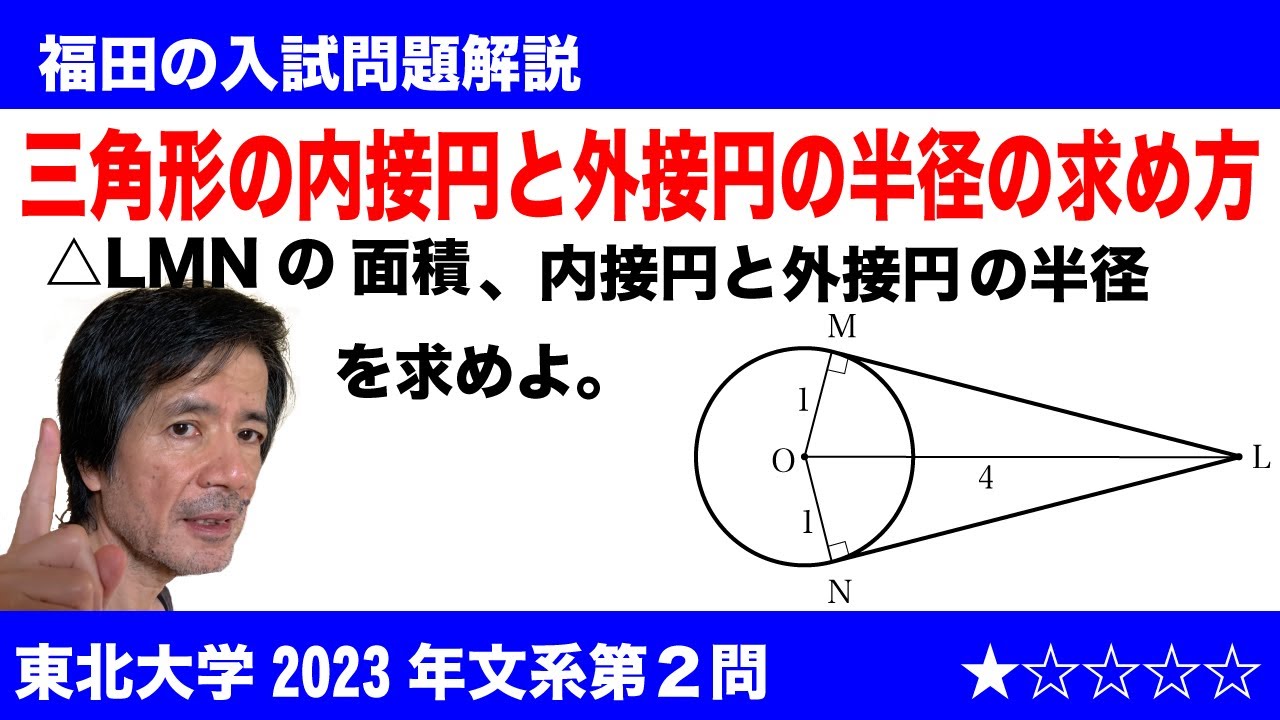
福田の数学〜東北大学2023年文系第1問〜三角形の面積と内接円と外接円の半径
単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#周角と円に内接する四角形・円と接線・接弦定理#三角関数#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 平面上の半径1の円Cの中心Oから距離4だけ離れた点Lをとる。点Lを通る円Cの2本の接線と円Cの接点をそれぞれM、Nとする。以下の問いに答えよ。
(1)三角形LMNの面積を求めよ。
(2)三角形LMNの内接円の半径をrと、三角形LMNの外接円の半径Rをそれぞれ求めよ。
2023東北大学文系過去問
この動画を見る
$\Large\boxed{2}$ 平面上の半径1の円Cの中心Oから距離4だけ離れた点Lをとる。点Lを通る円Cの2本の接線と円Cの接点をそれぞれM、Nとする。以下の問いに答えよ。
(1)三角形LMNの面積を求めよ。
(2)三角形LMNの内接円の半径をrと、三角形LMNの外接円の半径Rをそれぞれ求めよ。
2023東北大学文系過去問
【数検準2級】高校数学:数学検定準2級2次:問5

単元:
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学検定#数学検定準2級#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問5. 次の問いに答えなさい。
(7) 地点Aから、湖を隔てた地点Bまでの距離を測定するために、地点Aから100m、地点Bから60m離れたところに地点Pをとります。地点Pから地点A、Bをみて$\angle APB$の大きさを調べたところ、$\angle APB=120°$でした。
このとき、2地点A、B間の距離は何mですか。余弦定理を用いて求めなさい。
この動画を見る
問5. 次の問いに答えなさい。
(7) 地点Aから、湖を隔てた地点Bまでの距離を測定するために、地点Aから100m、地点Bから60m離れたところに地点Pをとります。地点Pから地点A、Bをみて$\angle APB$の大きさを調べたところ、$\angle APB=120°$でした。
このとき、2地点A、B間の距離は何mですか。余弦定理を用いて求めなさい。
シンプルだけど気付きにくい 円の問題 筑波大附属
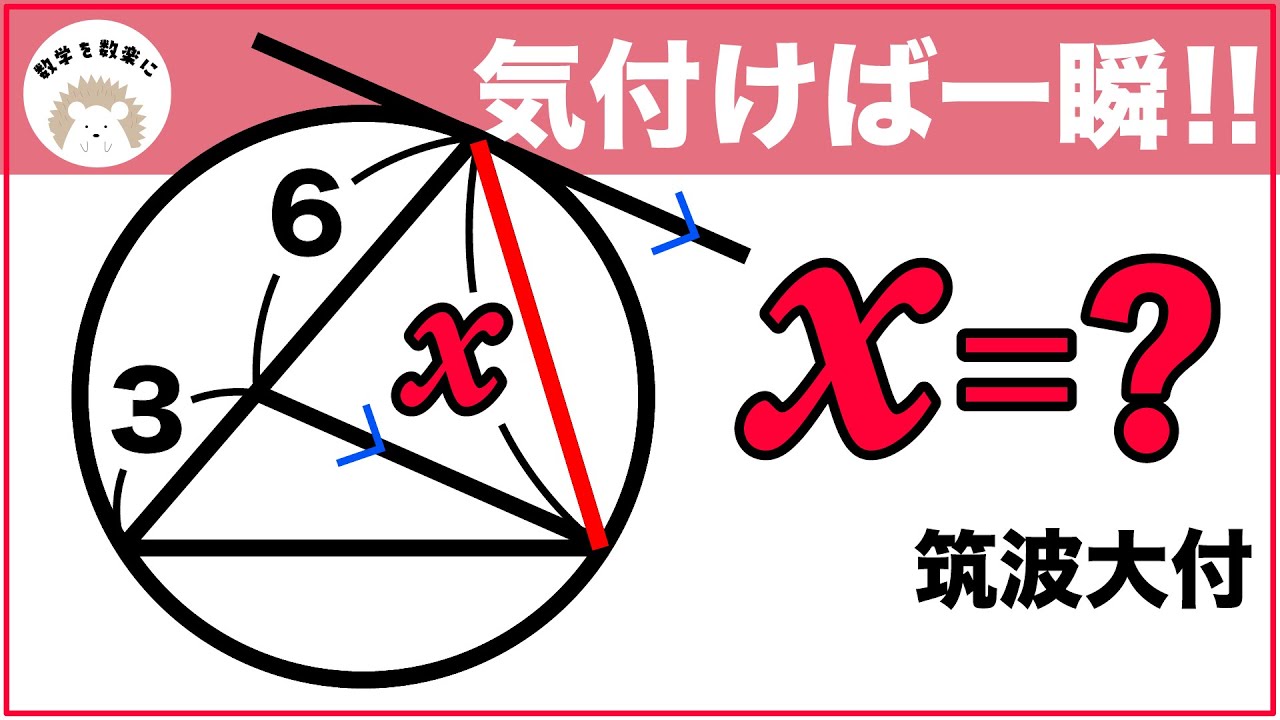
2つの正方形
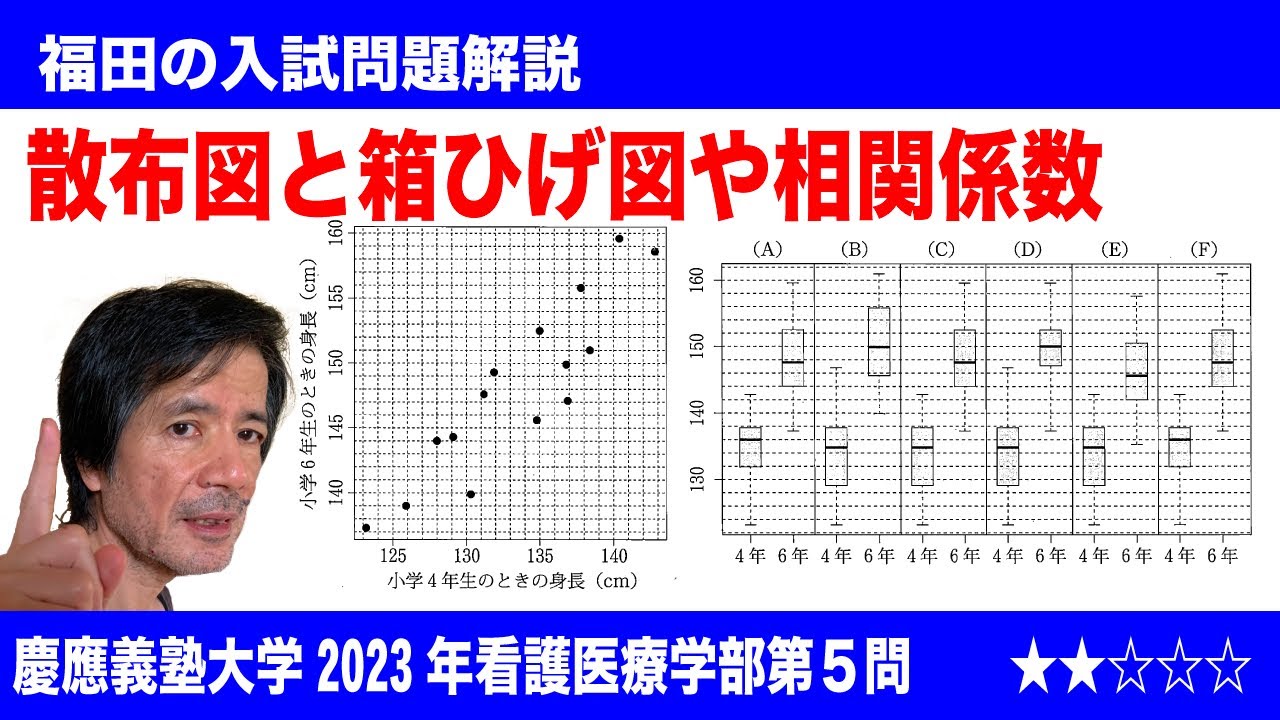
福田の数学〜慶應義塾大学2023年看護医療学部第5問〜散布図と箱ひげ図の関係と相関係数
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#データの分析#データの分析#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 以下の図は、ある小学校の15人の女子児童の4年生の4月に計測した身長を横軸に、5年生の4月に計測した身長を縦軸にとった散布図である。(※動画参照)
と表すことができる。よってS(a)を最小にするaはa=$\boxed{\ \ ミ\ \ }$である。
S(a)の最小値は、女子児童の4年生のときと6年生のときの身長の相関係数rと$s_y^2$を用いて$\boxed{\ \ ム\ \ }$と表せる。
また、左の散布図で示した女子児童の計測値を計算すると
$s_x^2$=29.00, $s_y^2$=42.65, $s_{xy}$=31.69
であった。これらを用いてS(a)を最小にするaを計算し、小数第4位を四捨五入すると$\boxed{\ \ メ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{5}$ 以下の図は、ある小学校の15人の女子児童の4年生の4月に計測した身長を横軸に、5年生の4月に計測した身長を縦軸にとった散布図である。(※動画参照)
と表すことができる。よってS(a)を最小にするaはa=$\boxed{\ \ ミ\ \ }$である。
S(a)の最小値は、女子児童の4年生のときと6年生のときの身長の相関係数rと$s_y^2$を用いて$\boxed{\ \ ム\ \ }$と表せる。
また、左の散布図で示した女子児童の計測値を計算すると
$s_x^2$=29.00, $s_y^2$=42.65, $s_{xy}$=31.69
であった。これらを用いてS(a)を最小にするaを計算し、小数第4位を四捨五入すると$\boxed{\ \ メ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
tan1°✖️ tan2°✖️tan3°✖️・・・✖️tan89°

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$tan1^ \circ \times tan2^ \circ \times tan3^ \circ \times \cdots tan88^ \circ \times tan89^ \circ$
この動画を見る
$tan1^ \circ \times tan2^ \circ \times tan3^ \circ \times \cdots tan88^ \circ \times tan89^ \circ$
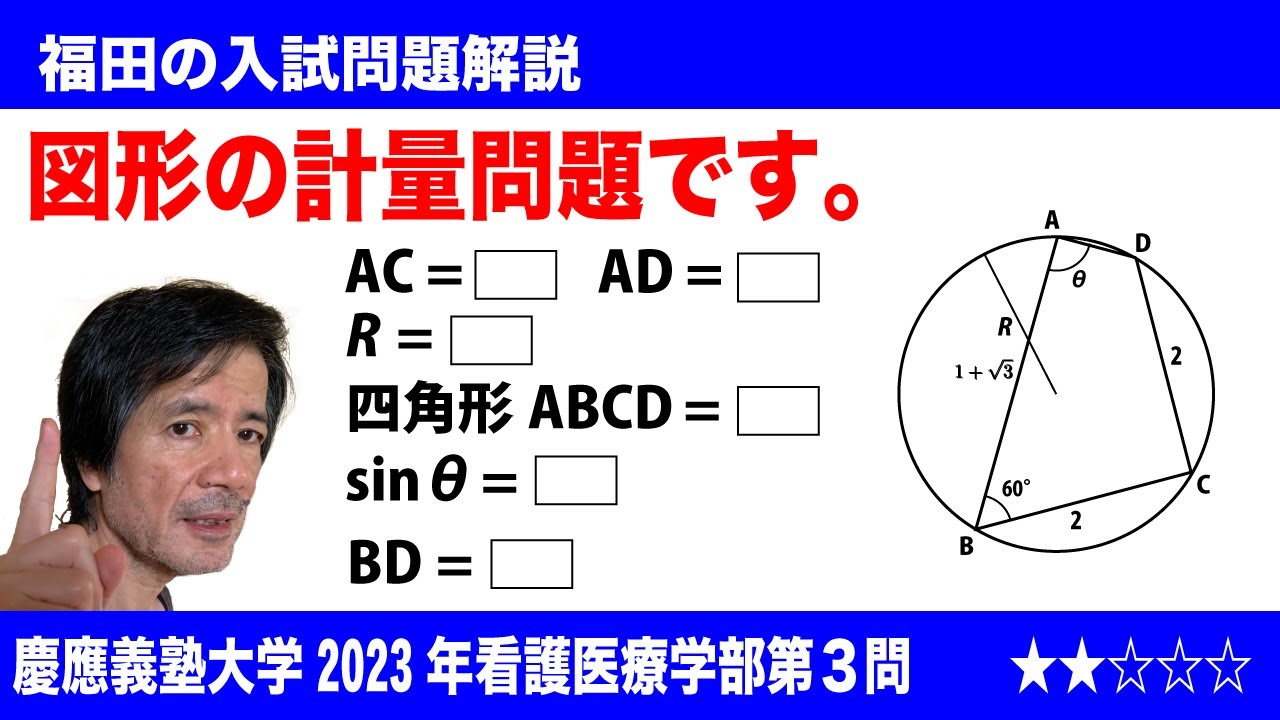
福田の数学〜慶應義塾大学2023年看護医療学部第3問〜三角比と図形の計量
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 半径Rの円に内接する四角形ABCDにおいて
AB=1+$\sqrt3$, BC=CD=2, $\angle$ABC=60°
であるとき、$\angle$ADCの大きさは$\angle$ADC=$\boxed{\ \ ソ\ \ }$であり、AC,AD,Rの長さはそれぞれAC=$\boxed{\ \ タ\ \ }$, AD=$\boxed{\ \ チ\ \ }$, R=$\boxed{\ \ ツ\ \ }$である。
また、四角形ABCDの面積は$\boxed{\ \ テ\ \ }$である。さらに、θ=$\angle$DABとするとき、$\sin\theta$=$\boxed{\ \ ト\ \ }$であり、BDの長さはBD=$\boxed{\ \ ナ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{3}$ 半径Rの円に内接する四角形ABCDにおいて
AB=1+$\sqrt3$, BC=CD=2, $\angle$ABC=60°
であるとき、$\angle$ADCの大きさは$\angle$ADC=$\boxed{\ \ ソ\ \ }$であり、AC,AD,Rの長さはそれぞれAC=$\boxed{\ \ タ\ \ }$, AD=$\boxed{\ \ チ\ \ }$, R=$\boxed{\ \ ツ\ \ }$である。
また、四角形ABCDの面積は$\boxed{\ \ テ\ \ }$である。さらに、θ=$\angle$DABとするとき、$\sin\theta$=$\boxed{\ \ ト\ \ }$であり、BDの長さはBD=$\boxed{\ \ ナ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
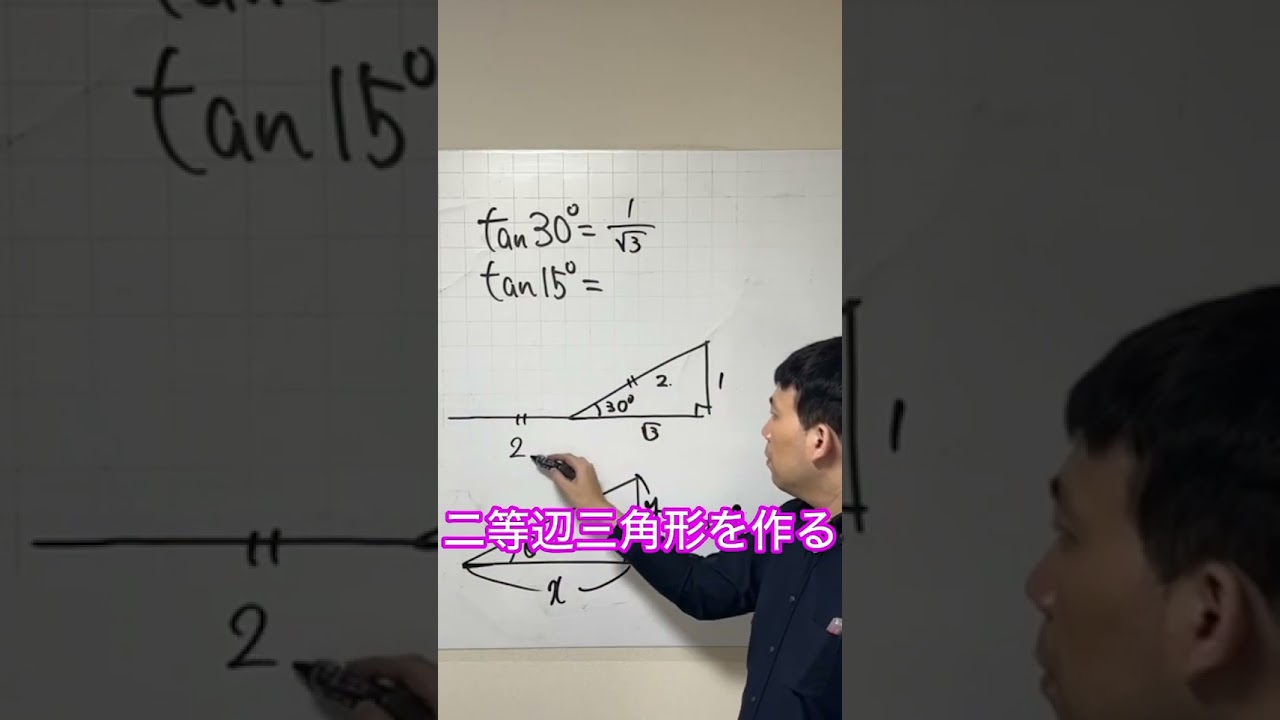
tan30° =❓ tan15°=❓
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
tan30°=
tan15°=
*図は動画内参照
この動画を見る
tan30°=
tan15°=
*図は動画内参照
図形と計量 多角形【NI・SHI・NOがていねいに解説】
単元:
#数Ⅰ#図形と計量#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
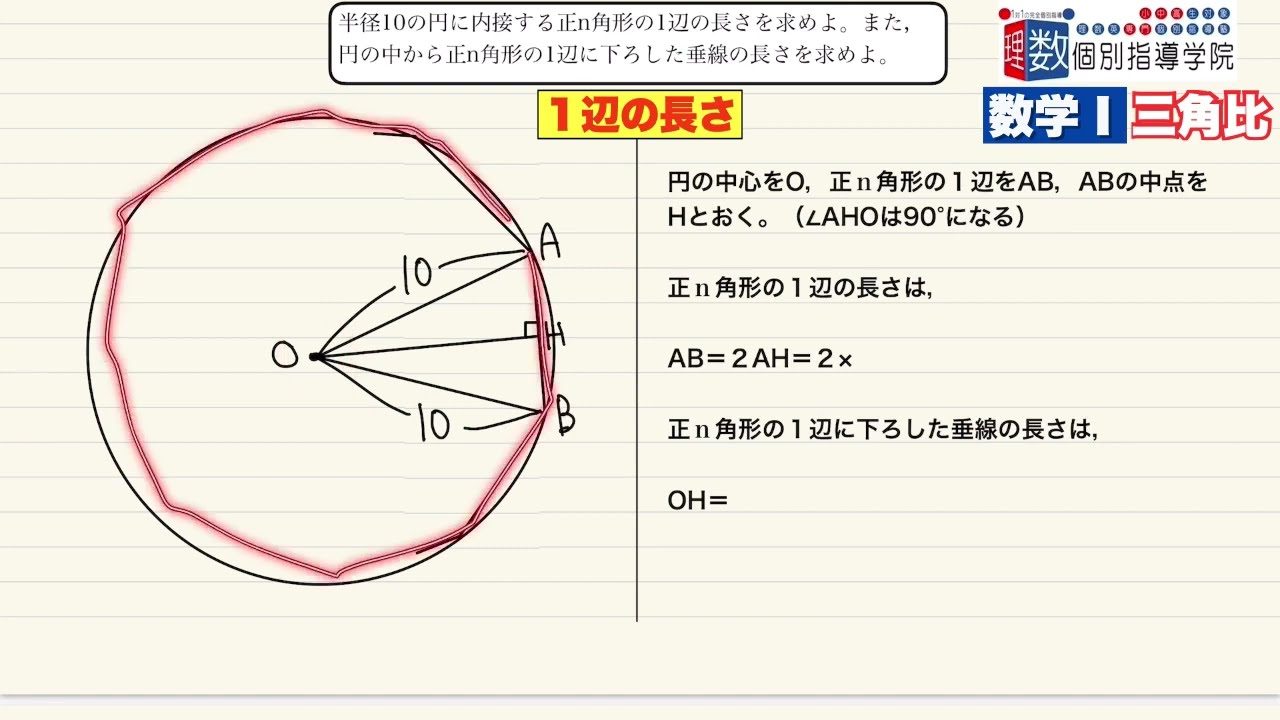
半径10の円に内接する正n角形の1辺の長さを求めよ。また,円の中心から正n角形の1辺に下ろした垂線の長さを求めよ。
この動画を見る
半径10の円に内接する正n角形の1辺の長さを求めよ。また,円の中心から正n角形の1辺に下ろした垂線の長さを求めよ。
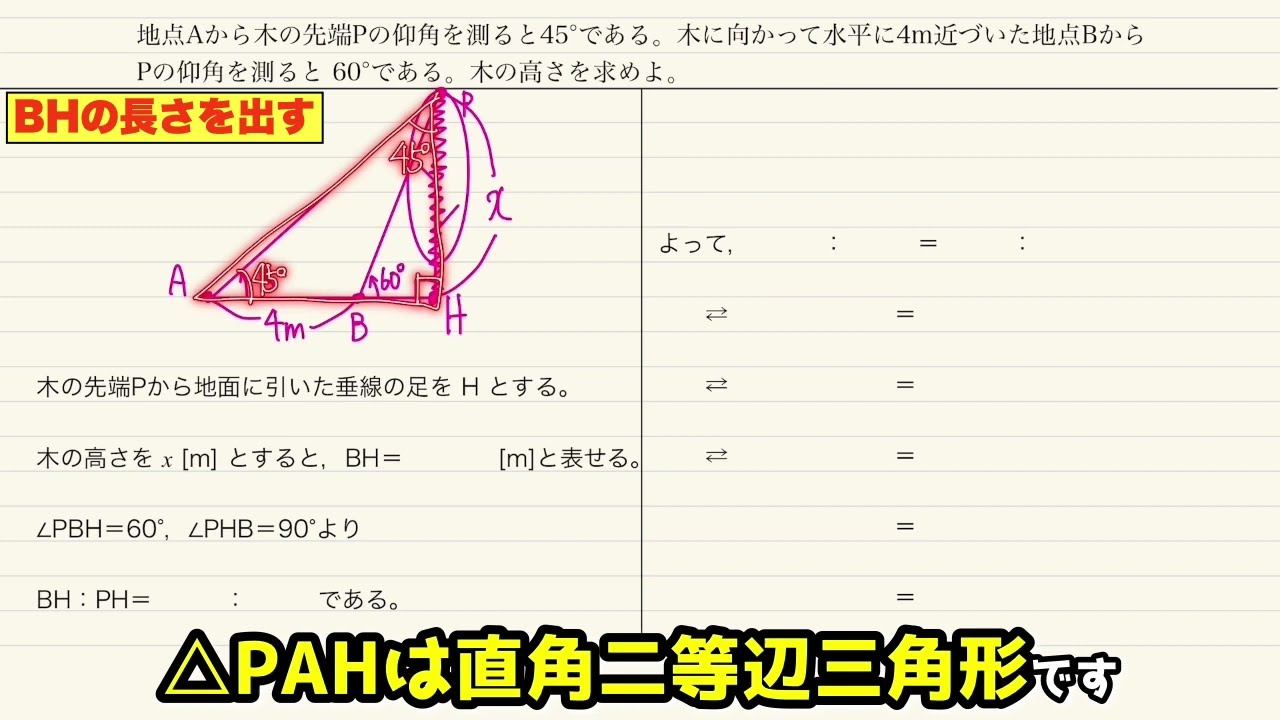
図形と計量 三角比応用 二か所からの測量【NI・SHI・NOがていねいに解説】
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\angle C=90°$ である直角三角形ABCにおいて,$\angle A=\theta, AB=k$ とする。頂点Cから辺ABに下ろした垂線を CD とするとき,次の線分の長さを$k,\theta$を用いて表せ。(1) $BC$ (2) $AC$ (3) $AD$ (4) $CD$ (5) $BD$
この動画を見る
$\angle C=90°$ である直角三角形ABCにおいて,$\angle A=\theta, AB=k$ とする。頂点Cから辺ABに下ろした垂線を CD とするとき,次の線分の長さを$k,\theta$を用いて表せ。(1) $BC$ (2) $AC$ (3) $AD$ (4) $CD$ (5) $BD$
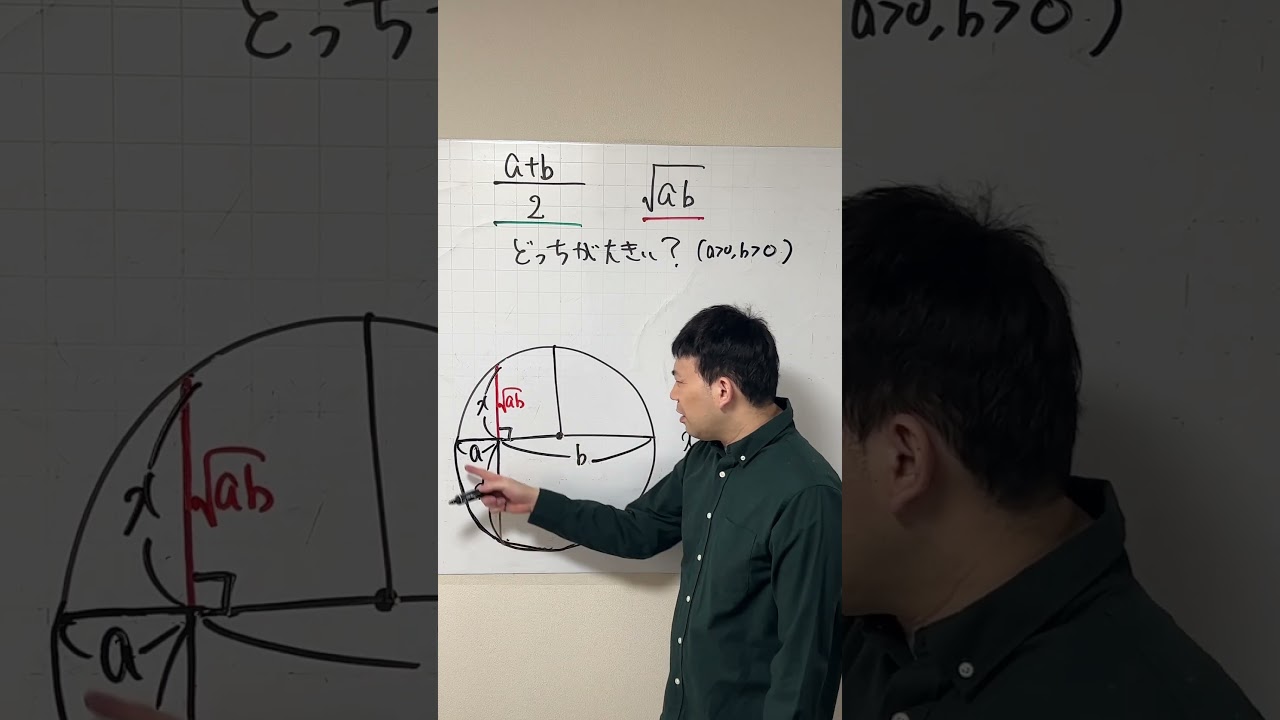
目で見てわかる 相加平均と相乗平均の関係
単元:
#数Ⅰ#図形と計量#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{a+b}{2}$ $\sqrt {ab}$
どっちが大きい?(a>0, b>0)
*図は動画内参照
この動画を見る
$\frac{a+b}{2}$ $\sqrt {ab}$
どっちが大きい?(a>0, b>0)
*図は動画内参照
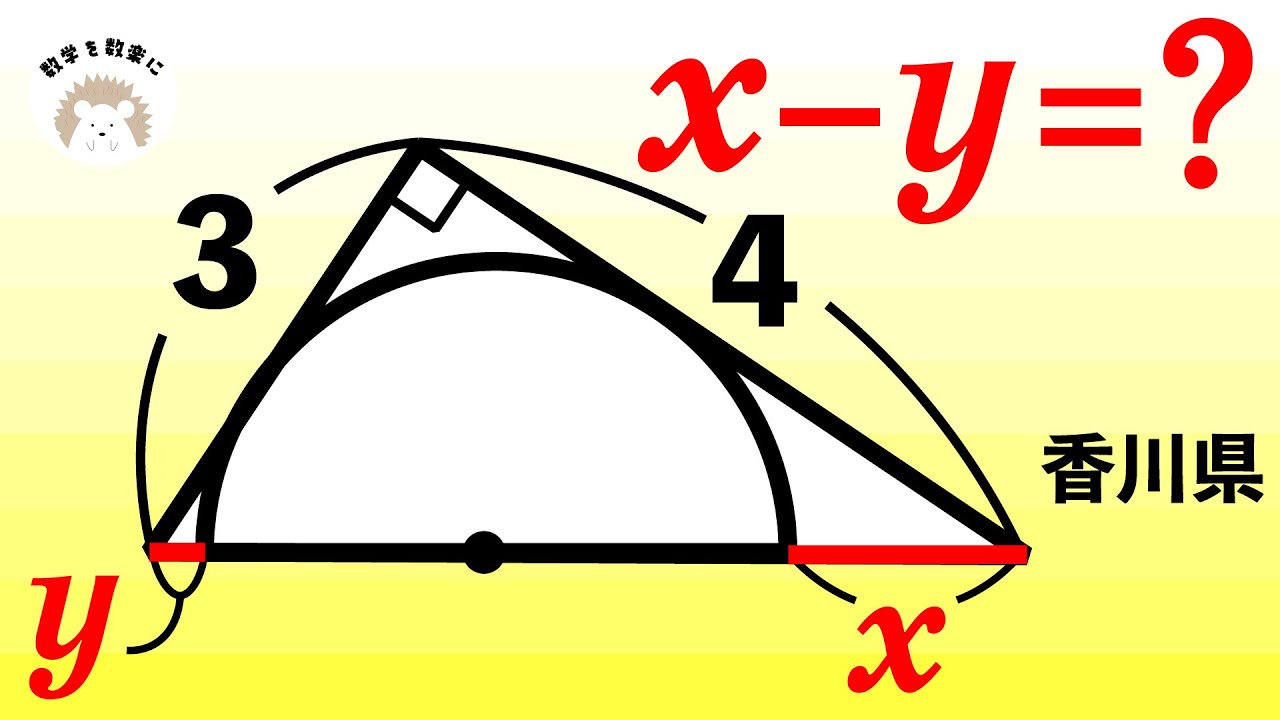
xとyは求まる。だがしかし。気付けば爽快!! 香川県 円
福田の数学〜慶應義塾大学2023年医学部第1問(1)〜図形の証明

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#式と証明#平面上のベクトル#図形と計量#三角比への応用(正弦・余弦・面積)#図形と方程式#恒等式・等式・不等式の証明#点と直線#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)三角形ABCにおいて辺BCを4:3に内分する点をDとするとき、等式
$\boxed{\ \ あ\ \ }$$AB^2$+$\boxed{\ \ い\ \ }$$AC^2$=$AD^2$+$\boxed{\ \ う\ \ }$$BD^2$
が成り立つ。
203慶應義塾大学医学部過去問
この動画を見る
$\Large\boxed{1}$ (1)三角形ABCにおいて辺BCを4:3に内分する点をDとするとき、等式
$\boxed{\ \ あ\ \ }$$AB^2$+$\boxed{\ \ い\ \ }$$AC^2$=$AD^2$+$\boxed{\ \ う\ \ }$$BD^2$
が成り立つ。
203慶應義塾大学医学部過去問
図形と計量 文字で三角比を表す【NI・SHI・NOがていねいに解説】

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\angle C=90°$ である直角三角形ABCにおいて,$\angle A=\theta, AB=k$ とする。頂点Cから辺ABに下ろした垂線を CD とするとき,次の線分の長さを$k,\theta$を用いて表せ。(1) BC (2) AC (3) AD (4) CD (5) BD
この動画を見る
$\angle C=90°$ である直角三角形ABCにおいて,$\angle A=\theta, AB=k$ とする。頂点Cから辺ABに下ろした垂線を CD とするとき,次の線分の長さを$k,\theta$を用いて表せ。(1) BC (2) AC (3) AD (4) CD (5) BD
図形と計量 建物の高さを求める【NI・SHI・NOがていねいに解説】
単元:
#数Ⅰ#図形と計量#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
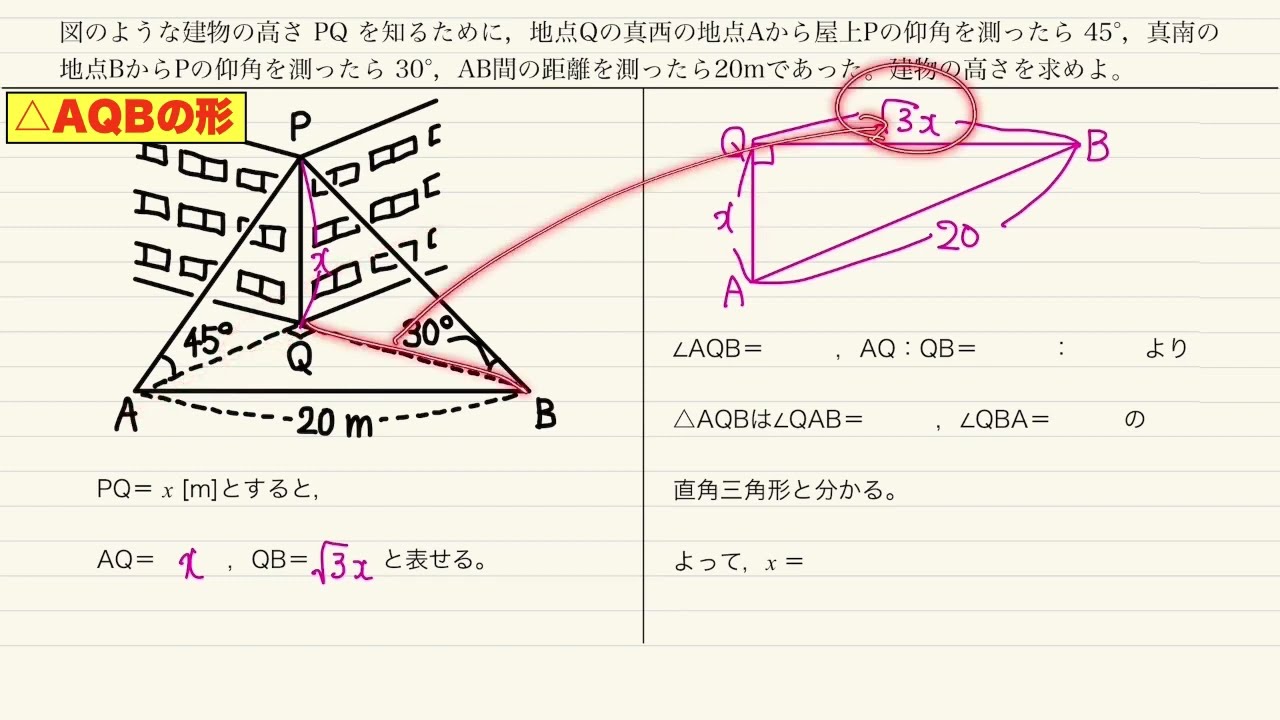
建物の高さ PQ を知るために,地点Qの真西の地点Aから屋上Pの仰角を測ったら 45°,真南の地点BからPの仰角を測ったら 30°,AB間の距離を測ったら20mであった。建物の高さを求めよ。
この動画を見る
建物の高さ PQ を知るために,地点Qの真西の地点Aから屋上Pの仰角を測ったら 45°,真南の地点BからPの仰角を測ったら 30°,AB間の距離を測ったら20mであった。建物の高さを求めよ。
図形と計量 三角比の空間への利用【NI・SHI・NOがていねいに解説】
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
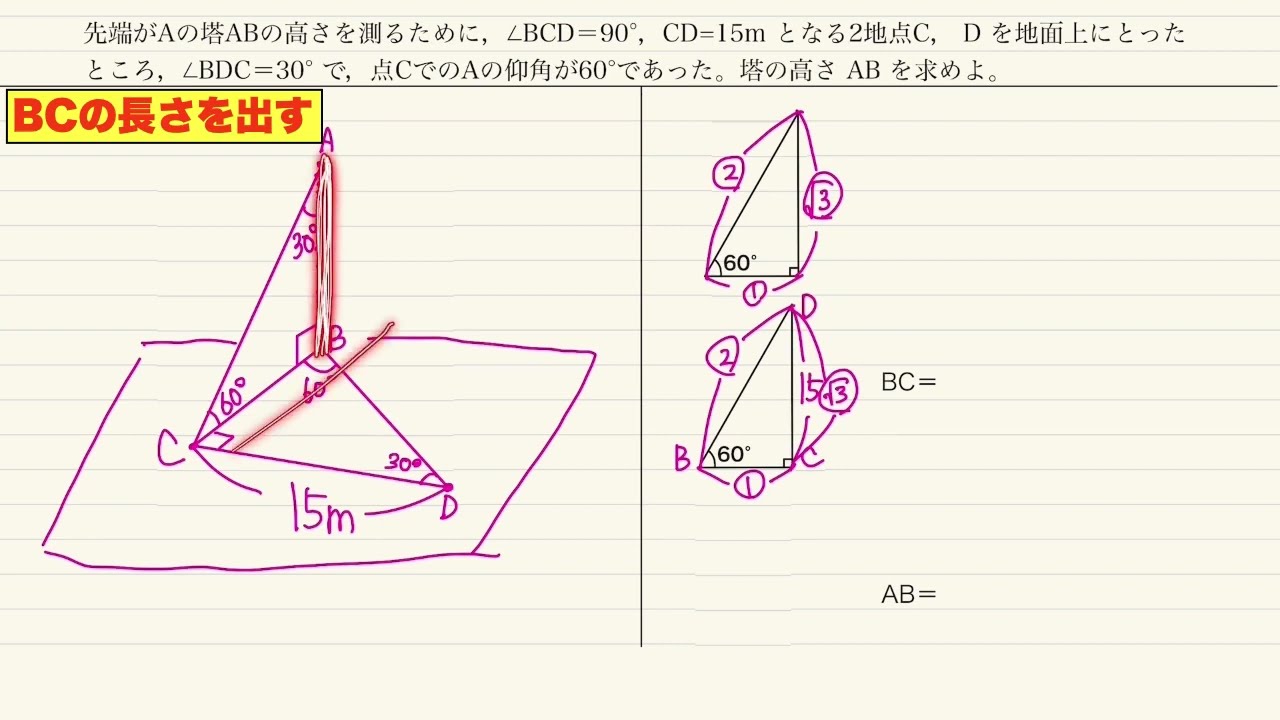
先端がAの塔ABの高さを測るために,$\angle BCD=90°,CD=15m$ となる2地点C, D を地面上にとったところ,$\angle BDC=30°$ で,点CでのAの仰角が$60°$であった。塔の高さ AB を求めよ。
この動画を見る
先端がAの塔ABの高さを測るために,$\angle BCD=90°,CD=15m$ となる2地点C, D を地面上にとったところ,$\angle BDC=30°$ で,点CでのAの仰角が$60°$であった。塔の高さ AB を求めよ。
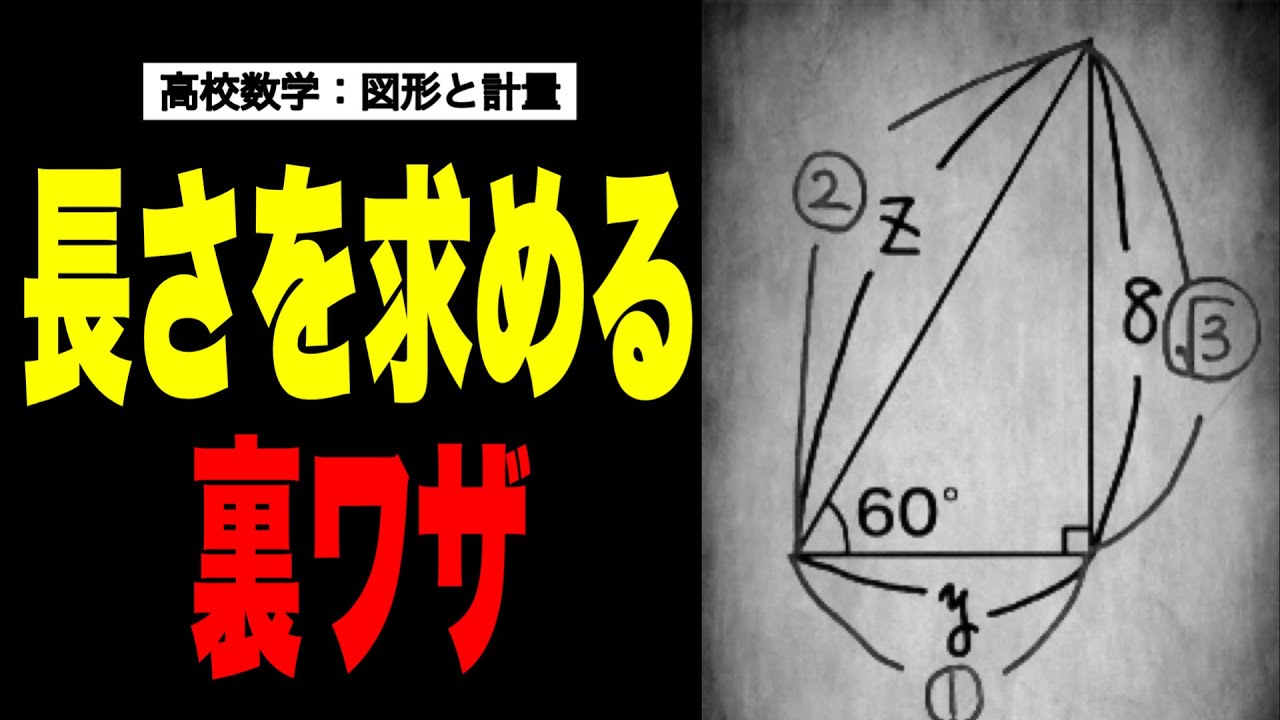
【数Ⅰ】図形と計量:三角比:3辺の比を求める裏ワザ!
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
有名角の三角比を使わずに辺の長さを出す裏ワザ!
この動画を見る
有名角の三角比を使わずに辺の長さを出す裏ワザ!
