 数Ⅰ
数Ⅰ
 数Ⅰ
数Ⅰ
【短時間でマスター!!】2次関数のグラフの書き方を解説!〔現役塾講師解説、数学〕

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
2次関数のグラフの書き方について解説します。
$y=x^2-6x+3$
$y=-2x^2+8x-3$
この動画を見る
数学1A
2次関数のグラフの書き方について解説します。
$y=x^2-6x+3$
$y=-2x^2+8x-3$
例の解法
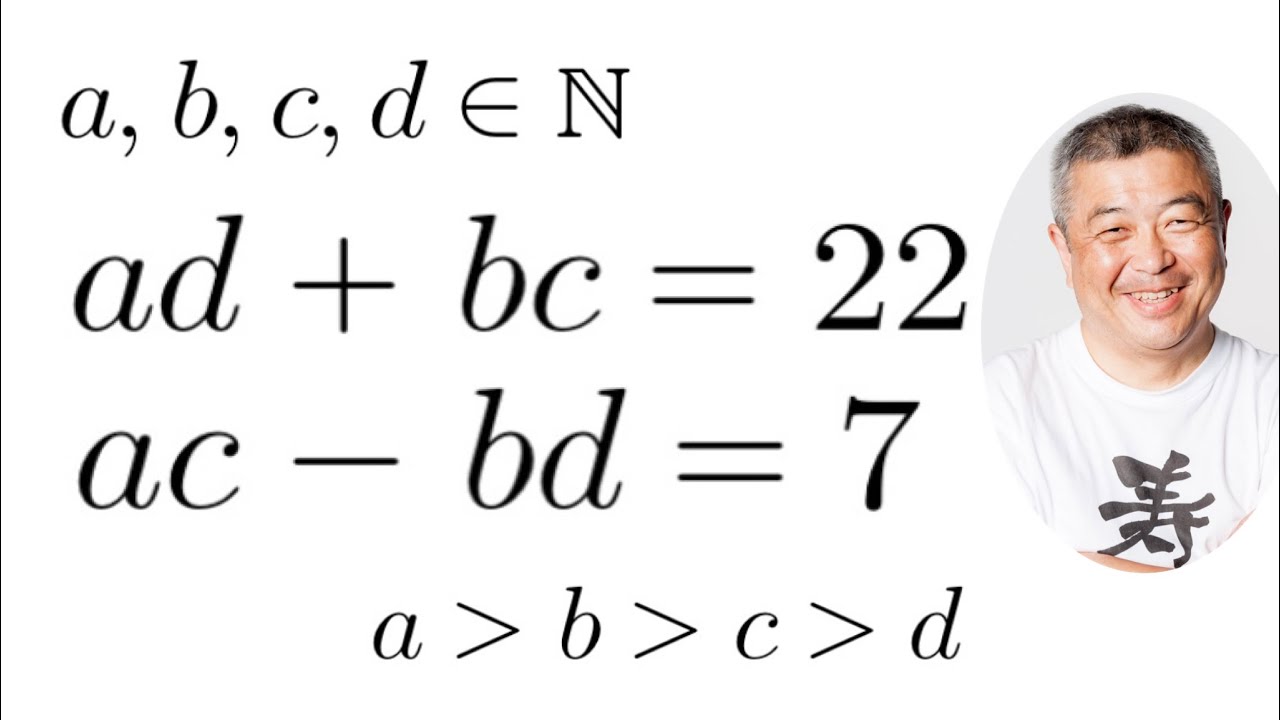
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
a,b,c,dは自然数であり,$a \gt b \gt c \gt d$である.
$ad+bc=22,ac-bd=7$
これを解け.
この動画を見る
a,b,c,dは自然数であり,$a \gt b \gt c \gt d$である.
$ad+bc=22,ac-bd=7$
これを解け.
方針は簡単、効率よく答えを出そう

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt{4n^2-12n-183}$が整数となる整数nをすべて求めよ.
この動画を見る
$ \sqrt{4n^2-12n-183}$が整数となる整数nをすべて求めよ.
福田の数学〜明治大学2022年全学部統一入試12AB第1問(4)〜角の二等分線と辺の長さの軽量

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(4)三角形$ABC$の$\angle A$の二等分線と辺$BC$との交点をDとする。
$AB=8,\ AC=3,\ AD=4$とするとき、
$BD:CD=\boxed{\ \ ソ\ \ }:\boxed{\ \ タ\ \ }$であり、
$BC=\frac{\boxed{\ \ チツ\ \ }\sqrt{\boxed{\ \ テ\ \ }}}{\boxed{\ \ ト\ \ }}$である。
2022明治大学全統過去問
この動画を見る
(4)三角形$ABC$の$\angle A$の二等分線と辺$BC$との交点をDとする。
$AB=8,\ AC=3,\ AD=4$とするとき、
$BD:CD=\boxed{\ \ ソ\ \ }:\boxed{\ \ タ\ \ }$であり、
$BC=\frac{\boxed{\ \ チツ\ \ }\sqrt{\boxed{\ \ テ\ \ }}}{\boxed{\ \ ト\ \ }}$である。
2022明治大学全統過去問
連立指数方程式

単元:
#数Ⅰ#数Ⅱ#数と式#式の計算(整式・展開・因数分解)#指数関数と対数関数#指数関数
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
3^{\frac{x}{2}}-2^y=7 \\
3^x-4^y=77
\end{array}
\right.
\end{eqnarray}$
これを解け.
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
3^{\frac{x}{2}}-2^y=7 \\
3^x-4^y=77
\end{array}
\right.
\end{eqnarray}$
これを解け.
ルートを外せ16 シリーズ史上最も難しい!!大阪星光学院

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
nは正の整数とする。
$\sqrt{n^2+2n+49}$が整数となるようなnを全て求めよ。
大阪星光学院
この動画を見る
nは正の整数とする。
$\sqrt{n^2+2n+49}$が整数となるようなnを全て求めよ。
大阪星光学院
福田の数学〜明治大学2022年全学部統一入試12AB第1問(2)〜対数方程式と対称式

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#複素数と方程式#式の計算(整式・展開・因数分解)#指数関数と対数関数#剰余の定理・因数定理・組み立て除法と高次方程式#対数関数#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(2)1ではない正の実数$x,\ y$が次の条件を満たすとする。
$\left\{\begin{array}{1}
xy=\displaystyle\frac{1}{4}\\
\displaystyle\frac{1}{\log_2x}+\displaystyle\frac{1}{\log_2y}=\frac{8}{21}
\end{array}\right.$
このとき、$x+y=\frac{\boxed{\ \ キク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}}{\boxed{\ \ コサ\ \ }}$である。
2022明治大学全統過去問
この動画を見る
(2)1ではない正の実数$x,\ y$が次の条件を満たすとする。
$\left\{\begin{array}{1}
xy=\displaystyle\frac{1}{4}\\
\displaystyle\frac{1}{\log_2x}+\displaystyle\frac{1}{\log_2y}=\frac{8}{21}
\end{array}\right.$
このとき、$x+y=\frac{\boxed{\ \ キク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}}{\boxed{\ \ コサ\ \ }}$である。
2022明治大学全統過去問
【短時間でマスター!!】平方完成の解き方を解説!〔現役塾講師解説、数学〕

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
平方完成の解き方について解説します。
$y=x^2-6x+3$
$y=-2x^2+8x-3$
この動画を見る
数学1A
平方完成の解き方について解説します。
$y=x^2-6x+3$
$y=-2x^2+8x-3$
【超便利】三角比のあの面倒な公式は覚えなくていい【高校数学】 #Shorts

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
三角比の導出方法に関して解説していきます。
この動画を見る
三角比の導出方法に関して解説していきます。
中学生にとっては激ムズすぎる 仙台育英(改)

単元:
#数学(中学生)#数Ⅰ#2次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式$2x^2-mx-m=0$の解の1つが1よりも大きいとき、mの値の範囲を求めよ。
(仙台育英学園高等学校 誘導省略)
この動画を見る
2次方程式$2x^2-mx-m=0$の解の1つが1よりも大きいとき、mの値の範囲を求めよ。
(仙台育英学園高等学校 誘導省略)
この問題で差がつく!!円の良問 近江高校(滋賀)
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
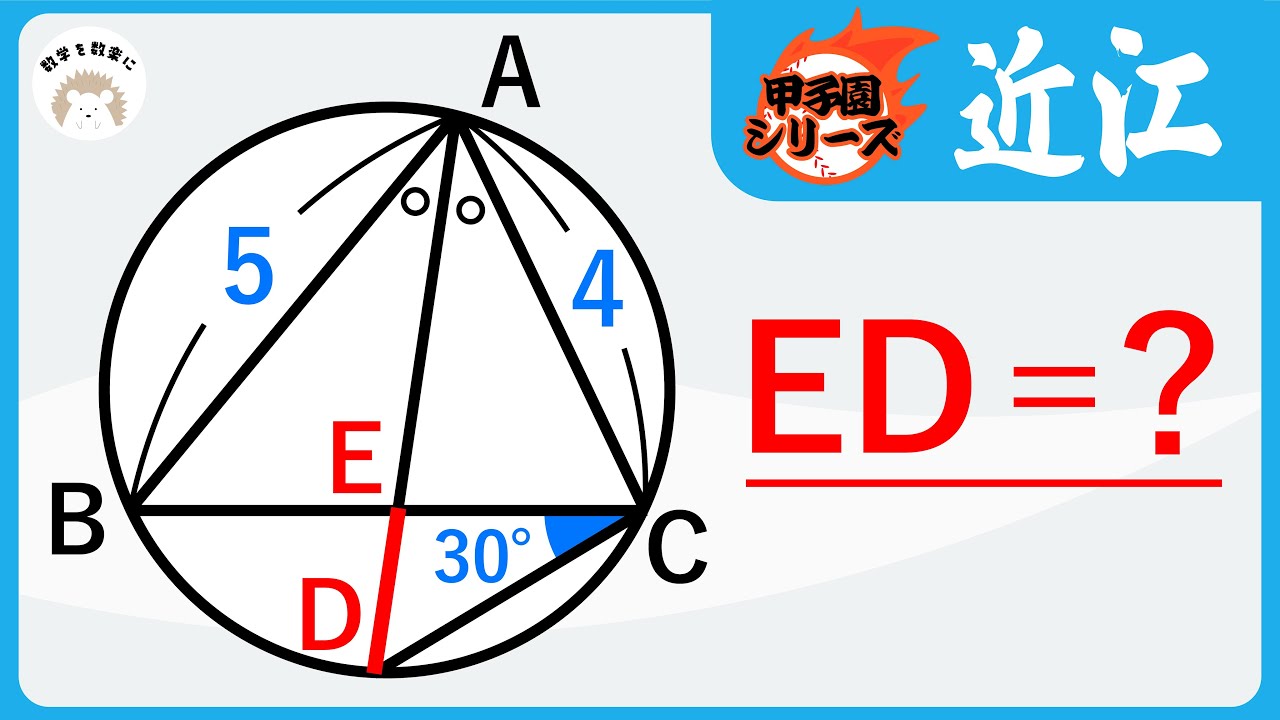
DE=?
*図は動画内参照
近江高等学校
この動画を見る
DE=?
*図は動画内参照
近江高等学校
4乗根の計算
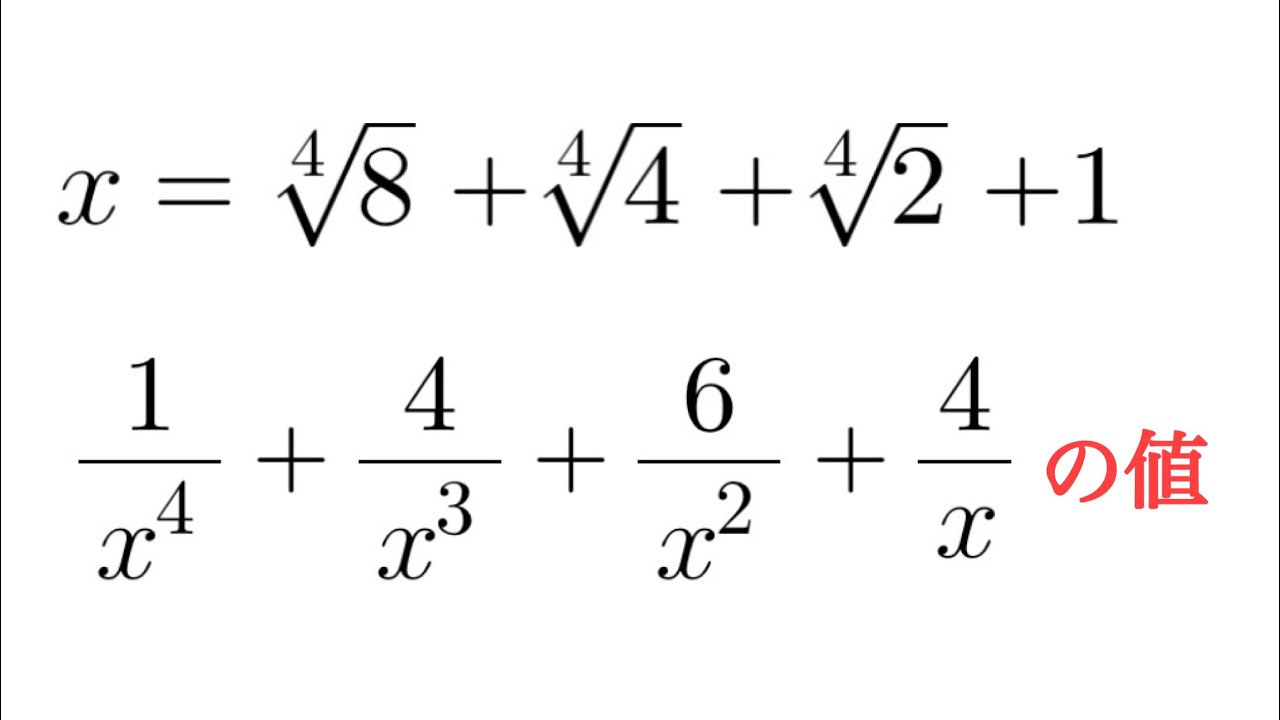
単元:
#数Ⅰ#数Ⅱ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x=\sqrt[4]{8}+\sqrt[4]{4}+\sqrt[4]{2}+1$のとき,
$\dfrac{1}{x^4}+\dfrac{4}{x^3}+\dfrac{6}{x^2}+\dfrac{4}{x}$の値を求めよ.
この動画を見る
$ x=\sqrt[4]{8}+\sqrt[4]{4}+\sqrt[4]{2}+1$のとき,
$\dfrac{1}{x^4}+\dfrac{4}{x^3}+\dfrac{6}{x^2}+\dfrac{4}{x}$の値を求めよ.
循環小数を分数に直す 近江高校

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$1.\dot{2} \dot{3}$を分数で表せ。
近江高等学校
この動画を見る
$1.\dot{2} \dot{3}$を分数で表せ。
近江高等学校
【中学から分かる!】正弦定理(2):三角比 特別講義(トッコー)~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\triangle ABC$において,$a \sin A=b \sin B=c \sin C$ならばどんな三角形か.
この動画を見る
$\triangle ABC$において,$a \sin A=b \sin B=c \sin C$ならばどんな三角形か.
因数分解 3通りで解説 (仙台育英)

単元:
#数学(中学生)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$xyz+x^2y-xy^2-x+y-z$を因数分解せよ
仙台育英学園高等学校
この動画を見る
$xyz+x^2y-xy^2-x+y-z$を因数分解せよ
仙台育英学園高等学校
気付けば一瞬!! 正六角形 九州学院(熊本)
単元:
#数学(中学生)#数Ⅰ#数A#図形の性質#図形と計量#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
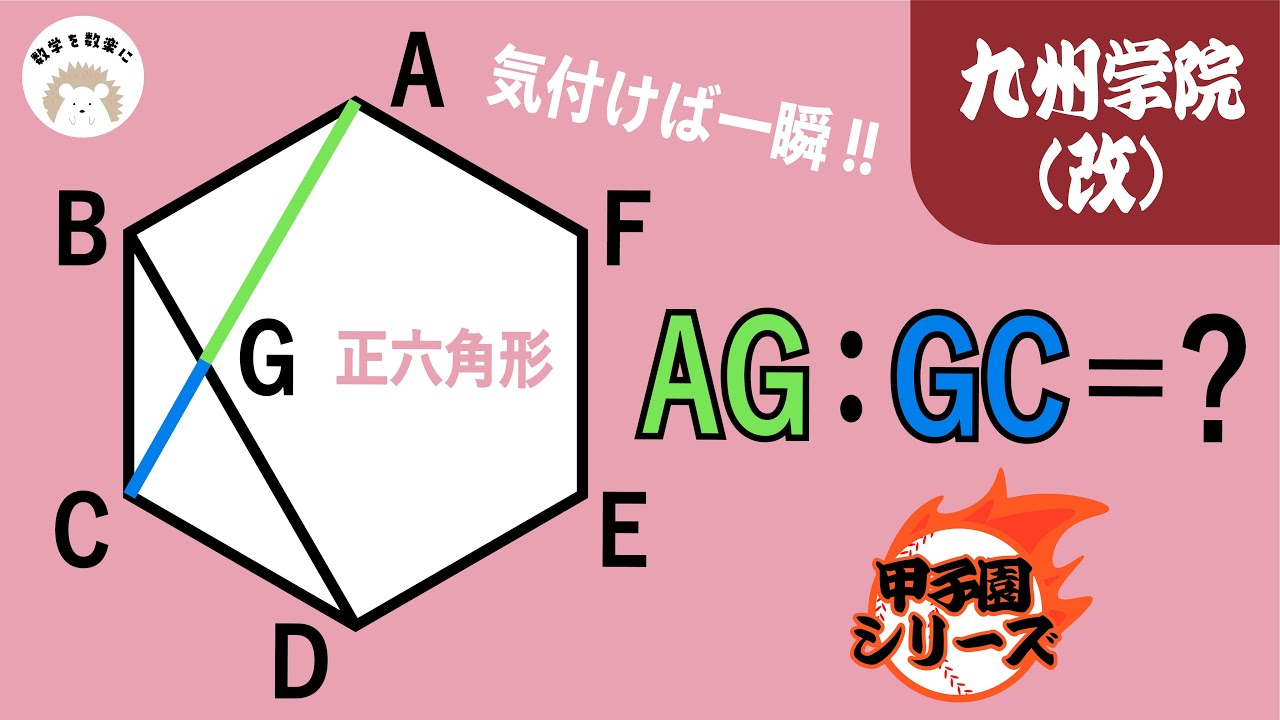
AG:GC=?
*図は動画内参照
九州学院高等学校(改)
この動画を見る
AG:GC=?
*図は動画内参照
九州学院高等学校(改)
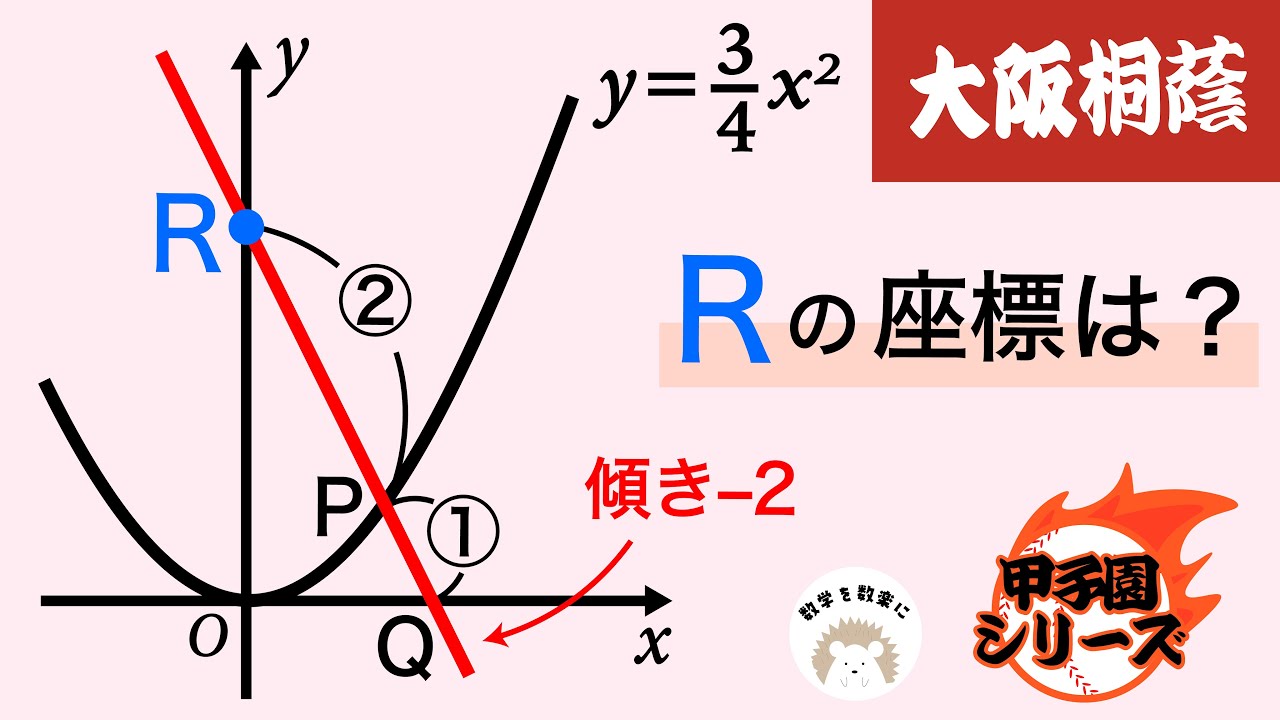
放物線と比 大阪桐蔭
単元:
#数学(中学生)#数Ⅰ#数Ⅱ#2次関数#三角関数#三角関数とグラフ#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
Rの座標は?
*図は動画内参照
大阪桐蔭高等学校
この動画を見る
Rの座標は?
*図は動画内参照
大阪桐蔭高等学校
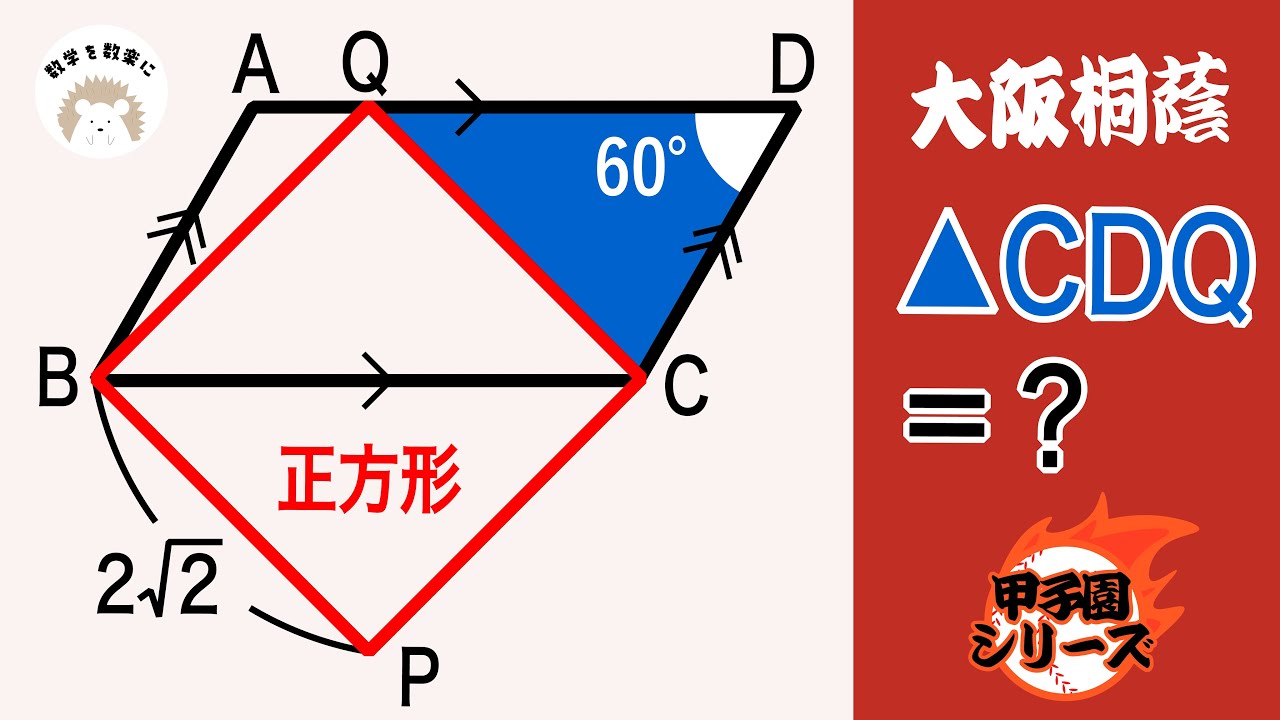
決め手は角度。大阪桐蔭
単元:
#数学(中学生)#数Ⅰ#数A#図形の性質#図形と計量#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△CDQ=?
*図は動画内参照
大阪桐蔭高等学校
この動画を見る
△CDQ=?
*図は動画内参照
大阪桐蔭高等学校
【中学から学ぶ!】正弦定理(1):三角比 特別講義~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \triangle ABC$において$ \sin^2 A=\sin^2 B+\sin^2 C$ならばどんな三角形か.
この動画を見る
$ \triangle ABC$において$ \sin^2 A=\sin^2 B+\sin^2 C$ならばどんな三角形か.
不定方程式
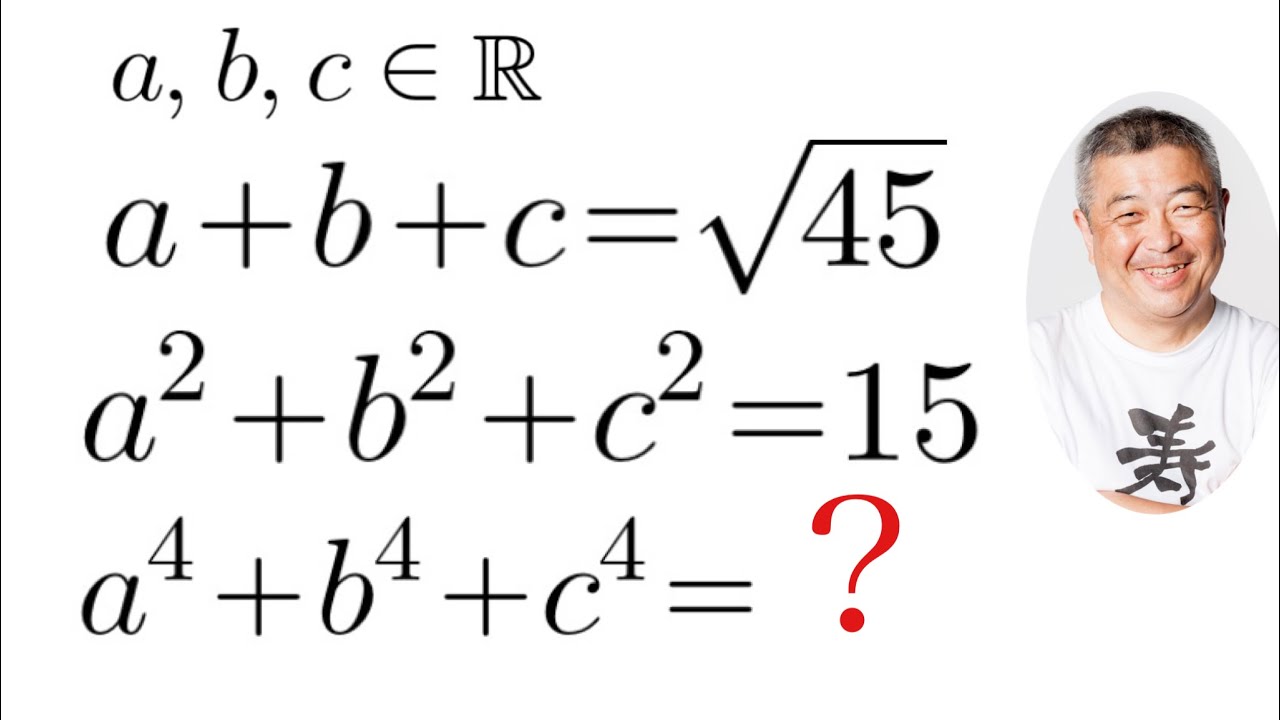
単元:
#数Ⅰ#数Ⅱ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
a,b,cは実数である.
$a+b+c=\sqrt{45}$
$a^2+b^2+c^2=15$
$a^4+b^4+c^4=?$
これを解け.
この動画を見る
a,b,cは実数である.
$a+b+c=\sqrt{45}$
$a^2+b^2+c^2=15$
$a^4+b^4+c^4=?$
これを解け.
福田の数学〜早稲田大学2022年商学部第1問(2)〜対称式と最大値

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(2)実数$x,y$が$x^2+y^2\leqq 3$を満たしているとき、
$x-y-xy$の最大値は$\boxed{\ \ イ\ \ }$である。
2022早稲田大学商学部過去問
この動画を見る
${\large\boxed{1}}$(2)実数$x,y$が$x^2+y^2\leqq 3$を満たしているとき、
$x-y-xy$の最大値は$\boxed{\ \ イ\ \ }$である。
2022早稲田大学商学部過去問
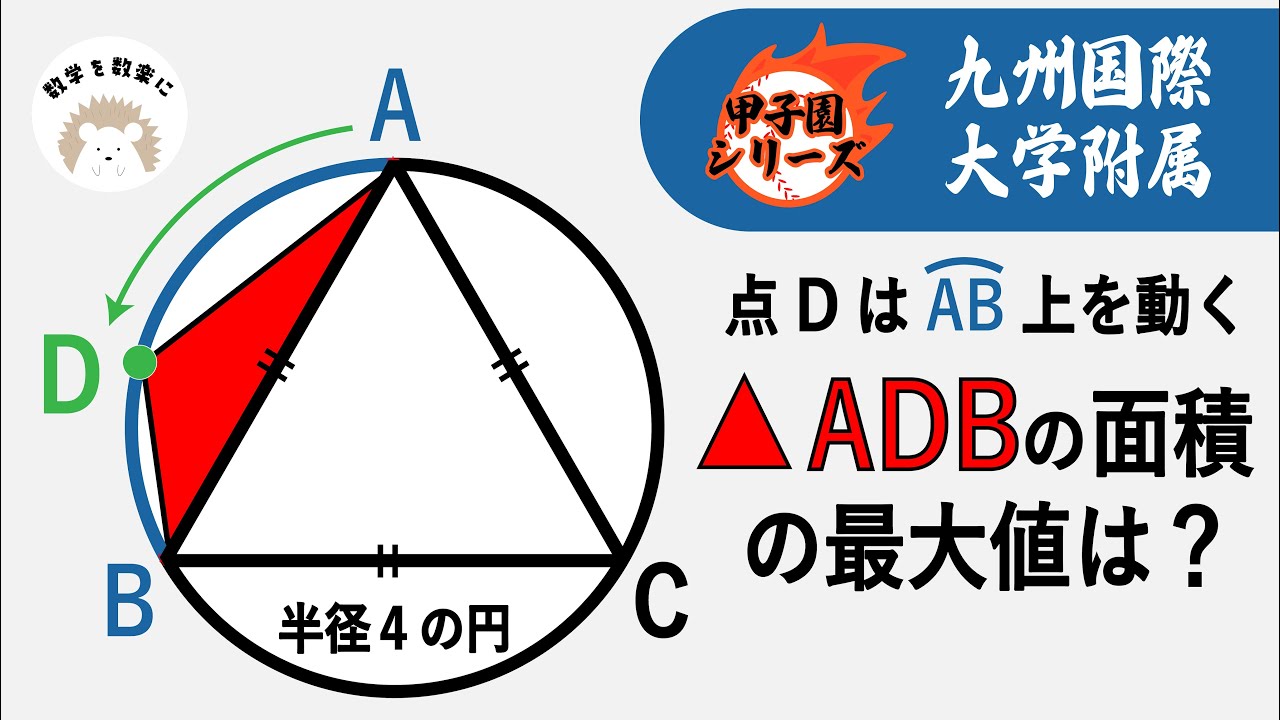
三角形の面積の最大値 九州国際大附属(福岡)
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
点Dは$\stackrel{\huge\frown}{AB}$上を動く△ADBの面積の最大値は?
*図は動画内参照
九州国際大学付属高等学校
この動画を見る
点Dは$\stackrel{\huge\frown}{AB}$上を動く△ADBの面積の最大値は?
*図は動画内参照
九州国際大学付属高等学校
式の値の範囲 仙台育英(宮城)
単元:
#数学(中学生)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#一次不等式(不等式・絶対値のある方程式・不等式)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$-3 \leqq x \leqq 4$ , $-6 \leqq y \leqq 11$
$㋐ \leqq x^2 +y^2 \leqq ㋑$
仙台育英学園高等学校
この動画を見る
$-3 \leqq x \leqq 4$ , $-6 \leqq y \leqq 11$
$㋐ \leqq x^2 +y^2 \leqq ㋑$
仙台育英学園高等学校
四分位範囲とは? 国学院栃木(栃木)

単元:
#数学(中学生)#数Ⅰ#データの分析#データの分析#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
0,1,1,2,2,2,2,3,3,3,3,4,5の四分位範囲は?
國學院大學栃木高等学校
この動画を見る
0,1,1,2,2,2,2,3,3,3,3,4,5の四分位範囲は?
國學院大學栃木高等学校
福田の数学〜早稲田大学2022年教育学部第3問〜円の外接円の半径と円周上の点と原点の距離の最大最小

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#図形と方程式#点と直線#円と方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{3}}\ O(0,0),\ A(0,1),\ B(p,q)$を座標平面上の点とし、pは0でないとする。
AとBを通る直線をlとおく。Oを中心としlに接する円の面積を$D_1$で表す。
また、3点O,A,Bを通る円周で囲まれる円の面積を$D_2$とおく。次の問いに答えよ。
(1)$D_1$を$p,q$を使って表せ。
(2)点$(2,2\sqrt3)$を中心とする半径1の円周をCとする。点BがC上を動くときの
$D_1$と$D_2$の積$D_1D_2$の最小値と最大値を求めよ。
2022早稲田大学教育学部過去問
この動画を見る
${\large\boxed{3}}\ O(0,0),\ A(0,1),\ B(p,q)$を座標平面上の点とし、pは0でないとする。
AとBを通る直線をlとおく。Oを中心としlに接する円の面積を$D_1$で表す。
また、3点O,A,Bを通る円周で囲まれる円の面積を$D_2$とおく。次の問いに答えよ。
(1)$D_1$を$p,q$を使って表せ。
(2)点$(2,2\sqrt3)$を中心とする半径1の円周をCとする。点BがC上を動くときの
$D_1$と$D_2$の積$D_1D_2$の最小値と最大値を求めよ。
2022早稲田大学教育学部過去問
度数分布表から平均値を求める 九州学院(熊本)
単元:
#数学(中学生)#数Ⅰ#データの分析#データの分析#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
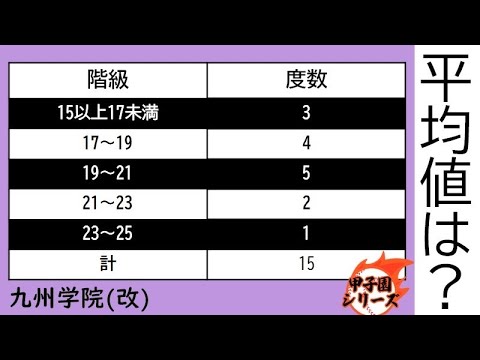
平均値=?
*図は動画内参照
九州学院高等学校(改)
この動画を見る
平均値=?
*図は動画内参照
九州学院高等学校(改)
【データの活用とは言うけれど…】統計:「箱ひげ図」とは!~全国入試問題解法
単元:
#数学(中学生)#データの分析#確率分布と統計的な推測#統計的な推測#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
箱ひげ図に関して解説していきます.
この動画を見る
箱ひげ図に関して解説していきます.
【因数分解】あるあるの難問!パターンを抑えたい数学の問題 #Shorts

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
因数分解せよ。
$x^4-16x^2+100$
この動画を見る
因数分解せよ。
$x^4-16x^2+100$
4乗根の有理化

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \left(1+\dfrac{1}{\sqrt[4]{8}+\sqrt{2}+\sqrt[4]{2}+1} \right)^{20}$
これを計算せよ.
この動画を見る
$ \left(1+\dfrac{1}{\sqrt[4]{8}+\sqrt{2}+\sqrt[4]{2}+1} \right)^{20}$
これを計算せよ.
福田の数学〜早稲田大学2022年教育学部第1問(3)〜四面体と四面体の共通部分の切り口の面積

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#図形と方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(3)座標空間内の4点$(2,0,0),\ (-1,\sqrt3,0),\ (-1,-\sqrt3,0),\ (0,0,2)$を頂点と
する四面体をP、4点$(-2,0,1),\ (1,-\sqrt3,1),\ (1,\sqrt3,1),\ (0,0,-1)$を頂点
とする四面体をQとする。RをPとQの共通部分とする。Rを平面$z=\frac{1}{3}$で
切ったときの切り口の面積を求めよ。
2022早稲田大学教育学部過去問
この動画を見る
${\large\boxed{1}}$(3)座標空間内の4点$(2,0,0),\ (-1,\sqrt3,0),\ (-1,-\sqrt3,0),\ (0,0,2)$を頂点と
する四面体をP、4点$(-2,0,1),\ (1,-\sqrt3,1),\ (1,\sqrt3,1),\ (0,0,-1)$を頂点
とする四面体をQとする。RをPとQの共通部分とする。Rを平面$z=\frac{1}{3}$で
切ったときの切り口の面積を求めよ。
2022早稲田大学教育学部過去問
