 数Ⅰ
数Ⅰ
 数Ⅰ
数Ⅰ
意外と苦戦!?
単元:
#数学(中学生)#中3数学#数Ⅰ#三平方の定理#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
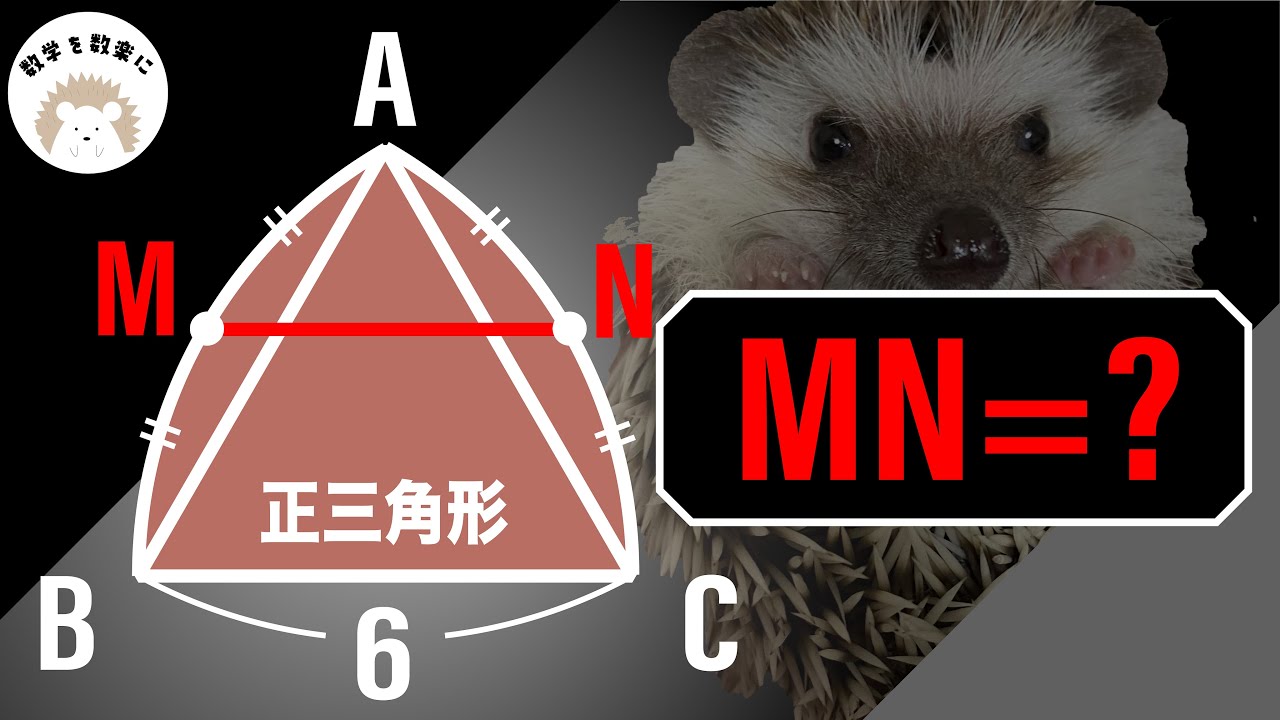
MN=?
*図は動画内参照
この動画を見る
MN=?
*図は動画内参照
確率×整数問題!さいころの目の最小公倍数や最大公約数【数学 入試問題】【北海道大学】

単元:
#数Ⅰ#数A#場合の数と確率#場合の数#確率#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n$を2以上の自然数とする。1個のさいころを続けて$n$回投げる試行を行い,出た目を順に$X_1,X_2,・・・,X_n$とする。
(1)$X_1,X_2,・・・,X_n$の最大公約数が3となる確率を$n$の式で表せ。
北海道大過去問
この動画を見る
$n$を2以上の自然数とする。1個のさいころを続けて$n$回投げる試行を行い,出た目を順に$X_1,X_2,・・・,X_n$とする。
(1)$X_1,X_2,・・・,X_n$の最大公約数が3となる確率を$n$の式で表せ。
北海道大過去問
【中学からの!】三角比の計算(2):特別講義(トッコー)~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\sin\theta+\cos\theta=\dfrac{1}{2}$のとき,$\sin^3\theta+\cos^3\theta$の値を求めよ.
この動画を見る
$\sin\theta+\cos\theta=\dfrac{1}{2}$のとき,$\sin^3\theta+\cos^3\theta$の値を求めよ.
大学入試問題#252 茨城大学(2012) #定積分

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#指数関数と対数関数#対数関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{log2}e^{|x|}e^xdx$を計算せよ。
出典:2012年茨城大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{log2}e^{|x|}e^xdx$を計算せよ。
出典:2012年茨城大学 入試問題
連立3元3次方程式
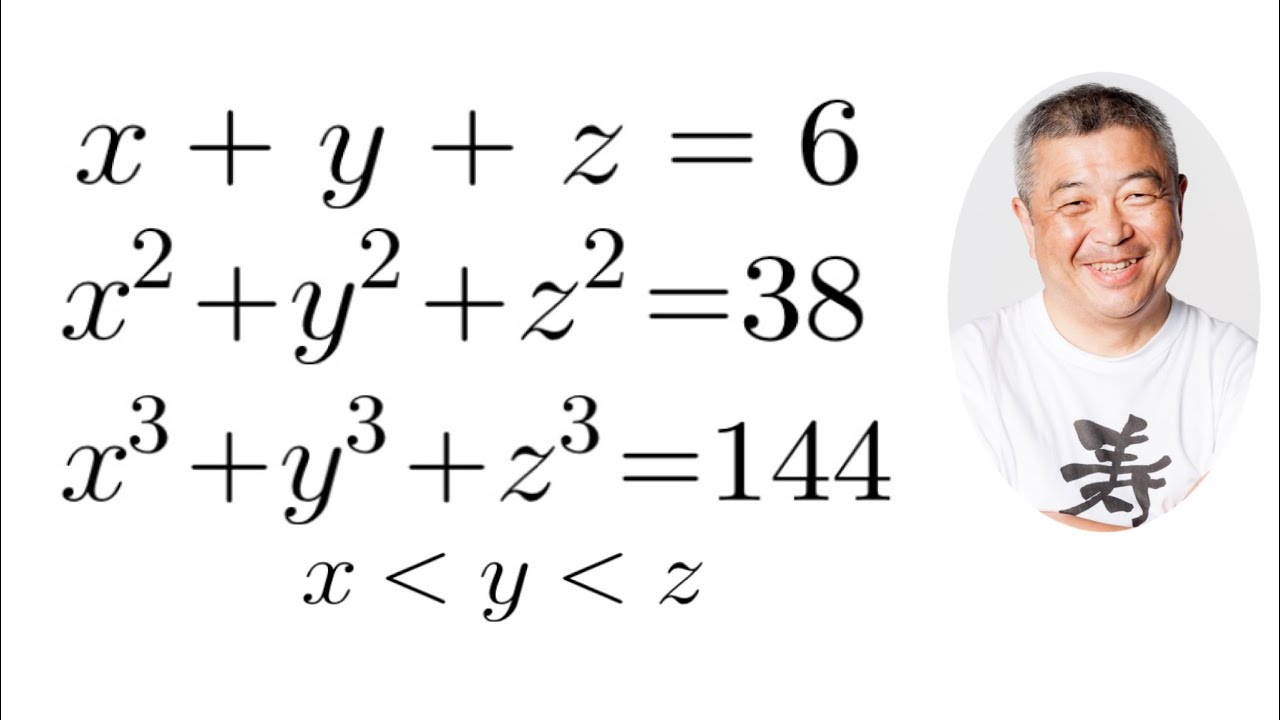
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x\lt y\lt z$とする.これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y+z=6 \\
x^2+y^2+z^2=38 \\\
x^3+y^3+z^3=144
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$x\lt y\lt z$とする.これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y+z=6 \\
x^2+y^2+z^2=38 \\\
x^3+y^3+z^3=144
\end{array}
\right.
\end{eqnarray}$
二重根号にビビるな! 東京電機大学

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt x = \sqrt {17 + \sqrt {253}} - \sqrt {17 - \sqrt {253}}$
整数xを求めよ
東京電機大学
この動画を見る
$\sqrt x = \sqrt {17 + \sqrt {253}} - \sqrt {17 - \sqrt {253}}$
整数xを求めよ
東京電機大学
ルートが出てきたら〇〇せよ! 式の値
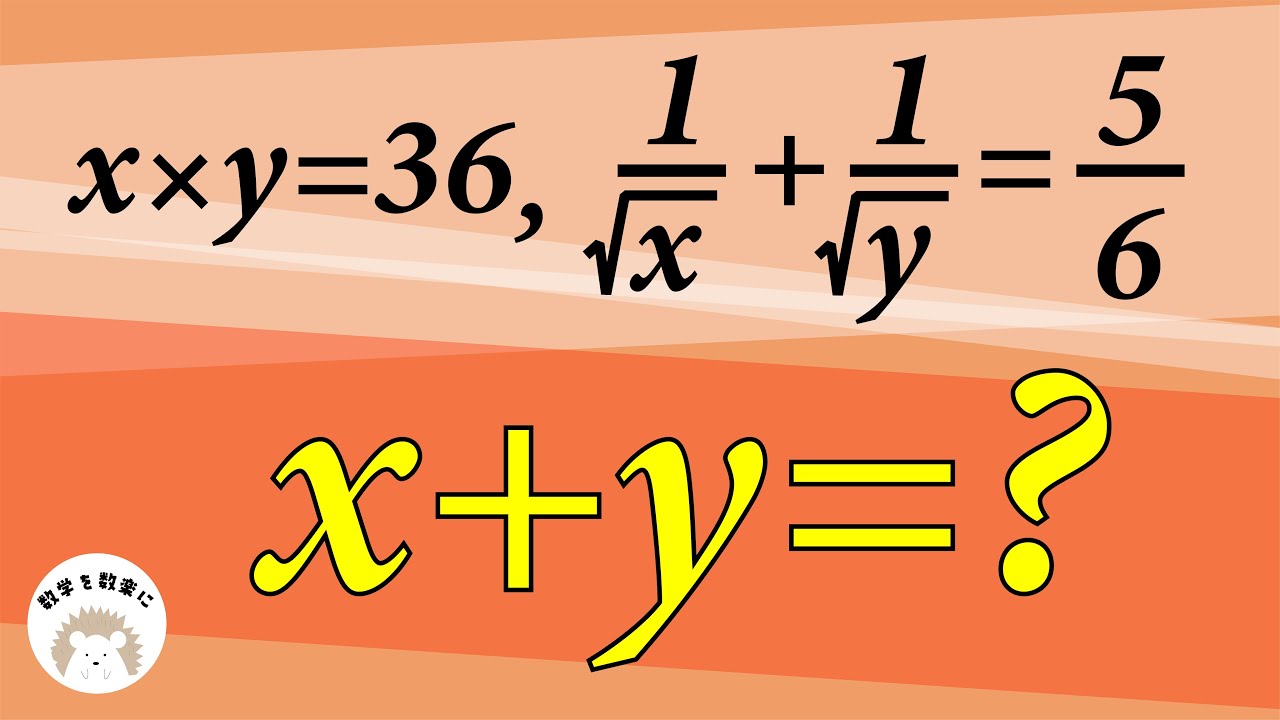
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x \times y = 36$ , $\frac{1}{\sqrt x} + \frac{1}{\sqrt y} = \frac{5}{6}$
$x+y=?$
この動画を見る
$x \times y = 36$ , $\frac{1}{\sqrt x} + \frac{1}{\sqrt y} = \frac{5}{6}$
$x+y=?$
【中学からの!】三角比の計算(1):特別講義(トッコー)~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\sin\theta+\cos\theta=\dfrac{1}{2}$のとき,$\sin\theta\cos\theta$の値を求めよ.
この動画を見る
$\sin\theta+\cos\theta=\dfrac{1}{2}$のとき,$\sin\theta\cos\theta$の値を求めよ.
高校範囲の因数分解
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
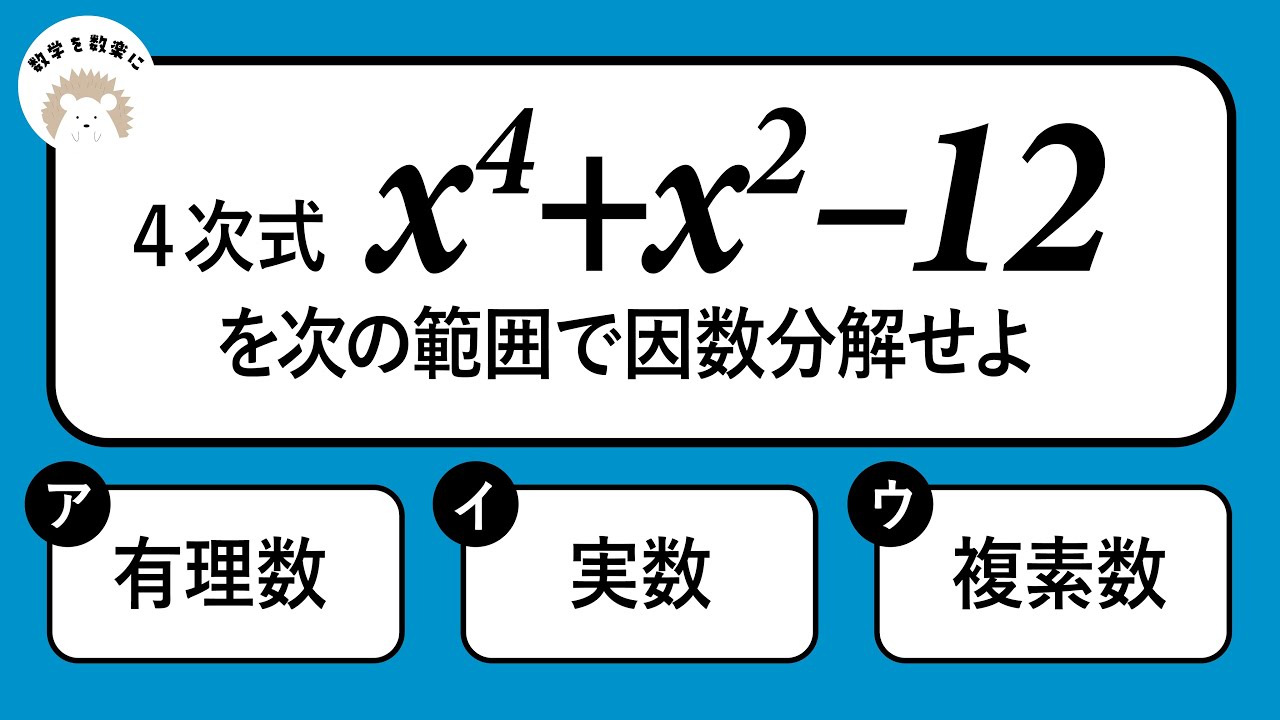
4次式$x^4+x^2-12$を次の範囲で因数分解せよ
㋐有理数
㋑実数
㋒複素数
この動画を見る
4次式$x^4+x^2-12$を次の範囲で因数分解せよ
㋐有理数
㋑実数
㋒複素数
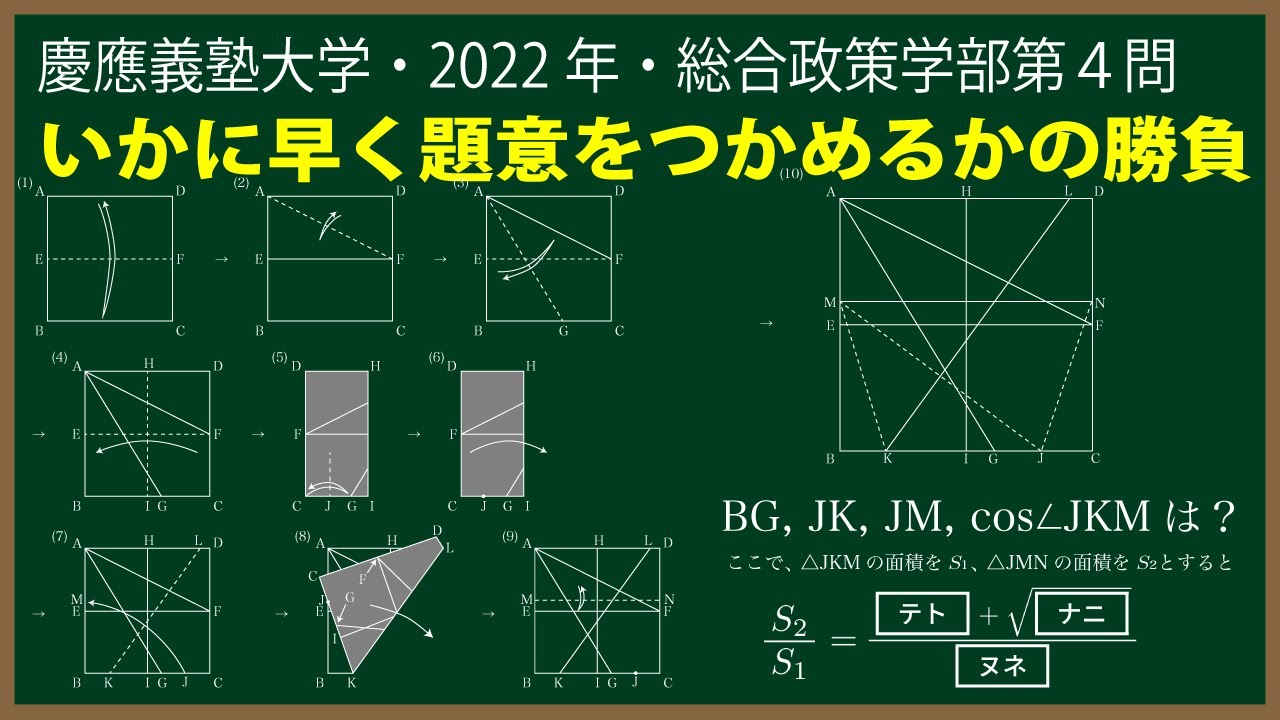
福田の数学〜慶應義塾大学2022年総合政策学部第4問〜折り紙を折ってできる線分、角、面積を求める
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{4}}$一辺の長さが2の正方形の折り紙 ABCD を次の手順にしたがって折る。
(1) A と B、DとCを合わせて ADがBCに重なるように谷折りし、折り目をつけて
開く。AB および DC 上にあるこの谷折り線の端点をそれぞれEおよびFとする。
(2 ) AF が谷折り線になるよう に谷折りし、折り目をつけて開く。
(3) A を谷折り線の端点の1つとして、AB がAF 上に重なるように谷折りし、折り
目をつけて開く。BC上にあるこの谷折り線のもう1つの端点をGとする。
(4) D と A、CとBを合わせてDCがABに重なるように谷折りして、折り目をつけ
る。AD およびBC 上にあるこの谷折り線の端点をそれぞれHおよびIとする。
(5) C と B がいずれもGと重なるように2枚重ねて谷折りし、CIおよびBI 上に折り
目をつけて開く。この折り目の点をそれぞれ」およびKとする (A, E, B, K は
それぞれ D, F, C, J と重なっているため図中には表示していない)
(6) HI を谷折り線とする谷折りを開く (A, E, B, KはそれぞれD, F, C, J と重なって
いるため図中には表示していない)
(7) K を谷折り線の端点の1つとして、JがAB上に重なるように谷折りし、折り目
をつける。AD上にあるこの谷折り線のもう1つの端点をしとし、AB上にある
Jが重なる点をMとする。
(8)KLを谷折り戦とする谷折りを開く(MはJと重なっているため表示していない)
(9)Mを谷折り線の端点の1つとして、AとDがそれぞれBEとCF上にくるように
谷折りし、折り目をつけて開く。DC上にあるこの谷折り線のもう1つ端点を
Nとする。
(10)折るのをやめる。
このとき、
$BG=\boxed{\ \ アイ\ \ }+\sqrt{\boxed{\ \ ウエ\ \ }},JK=\boxed{\ \ オカ\ \ }+\sqrt{\boxed{\ \ キク\ \ }},JM=\boxed{\ \ ケコ\ \ },$
$\cos\angle JKM=\frac{\boxed{\ \ サシ\ \ }+\boxed{\ \ スセ\ \ }\sqrt{\boxed{\ \ ソタ\ \ }}}{\boxed{\ \ チツ\ \ }}$
ここで、$\triangle JKM$の面積を$S_1,\triangle JMN$の面積を$S_2$とすると
$\frac{S_2}{S_1}=\frac{\boxed{\ \ テト\ \ }+\sqrt{\boxed{\ \ ナニ\ \ }}}{\boxed{\ \ ヌネ\ \ }}$
となる。
※(1)~(10)の画像は動画参照
2022慶應義塾大学総合政策学部過去問
この動画を見る
${\large\boxed{4}}$一辺の長さが2の正方形の折り紙 ABCD を次の手順にしたがって折る。
(1) A と B、DとCを合わせて ADがBCに重なるように谷折りし、折り目をつけて
開く。AB および DC 上にあるこの谷折り線の端点をそれぞれEおよびFとする。
(2 ) AF が谷折り線になるよう に谷折りし、折り目をつけて開く。
(3) A を谷折り線の端点の1つとして、AB がAF 上に重なるように谷折りし、折り
目をつけて開く。BC上にあるこの谷折り線のもう1つの端点をGとする。
(4) D と A、CとBを合わせてDCがABに重なるように谷折りして、折り目をつけ
る。AD およびBC 上にあるこの谷折り線の端点をそれぞれHおよびIとする。
(5) C と B がいずれもGと重なるように2枚重ねて谷折りし、CIおよびBI 上に折り
目をつけて開く。この折り目の点をそれぞれ」およびKとする (A, E, B, K は
それぞれ D, F, C, J と重なっているため図中には表示していない)
(6) HI を谷折り線とする谷折りを開く (A, E, B, KはそれぞれD, F, C, J と重なって
いるため図中には表示していない)
(7) K を谷折り線の端点の1つとして、JがAB上に重なるように谷折りし、折り目
をつける。AD上にあるこの谷折り線のもう1つの端点をしとし、AB上にある
Jが重なる点をMとする。
(8)KLを谷折り戦とする谷折りを開く(MはJと重なっているため表示していない)
(9)Mを谷折り線の端点の1つとして、AとDがそれぞれBEとCF上にくるように
谷折りし、折り目をつけて開く。DC上にあるこの谷折り線のもう1つ端点を
Nとする。
(10)折るのをやめる。
このとき、
$BG=\boxed{\ \ アイ\ \ }+\sqrt{\boxed{\ \ ウエ\ \ }},JK=\boxed{\ \ オカ\ \ }+\sqrt{\boxed{\ \ キク\ \ }},JM=\boxed{\ \ ケコ\ \ },$
$\cos\angle JKM=\frac{\boxed{\ \ サシ\ \ }+\boxed{\ \ スセ\ \ }\sqrt{\boxed{\ \ ソタ\ \ }}}{\boxed{\ \ チツ\ \ }}$
ここで、$\triangle JKM$の面積を$S_1,\triangle JMN$の面積を$S_2$とすると
$\frac{S_2}{S_1}=\frac{\boxed{\ \ テト\ \ }+\sqrt{\boxed{\ \ ナニ\ \ }}}{\boxed{\ \ ヌネ\ \ }}$
となる。
※(1)~(10)の画像は動画参照
2022慶應義塾大学総合政策学部過去問
【保存版】絶対値の方程式の裏技

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
絶対値の方程式の裏技紹介動画です
この動画を見る
絶対値の方程式の裏技紹介動画です
【超難問】3×2×1=??が難しすぎる世界
単元:
#数Ⅰ#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
深読みしすぎた$3 \times 2 \times 1$の計算
この動画を見る
深読みしすぎた$3 \times 2 \times 1$の計算
式の値 立教大

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a-b+c = 1$ , $a^2+b^2+c^2 = 29$のとき
$ac - ab -bc$の値を求めよ
立教大学
この動画を見る
$a-b+c = 1$ , $a^2+b^2+c^2 = 29$のとき
$ac - ab -bc$の値を求めよ
立教大学
福田の数学〜慶應義塾大学2022年商学部第3問〜絶対値の付いた2次関数のグラフと直線の共有点と面積

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#2次関数#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$mを実数とし、関数$y=|x^2-5x+4|$のグラフをC、直線$y=mx$を$l$とする。
(1)グラフCと直線lの共有点の個数は
$\boxed{\ \ アイ\ \ } \lt m \lt \boxed{\ \ ウ\ \ }$のとき0個
$m=\boxed{\ \ エオ\ \ }$のとき1個
$m \lt \boxed{\ \ カキ\ \ },\ m=\boxed{\ \ ク\ \ }$,または$m \gt \boxed{\ \ ケ\ \ }$のとき2個
$m=\boxed{\ \ コ\ \ }$のとき3個
$\boxed{\ \ サ\ \ } \lt m \lt \boxed{\ \ シ\ \ }$のとき4個
以下、グラフCと直線lの共有点の個数が3個の場合を考え、
グラフCと直線lの共有点を、x座標が小さい順にP,Q,Rとする。
(2)3点P,Q,Rのx座標は、順に$\boxed{\ \ ス\ \ }-\sqrt{\boxed{\ \ セ\ \ }},\ \boxed{\ \ ソ\ \ },\ \boxed{\ \ タ\ \ }+\sqrt{\boxed{\ \ チ\ \ }}$である。
(3)グラフCと線分QRで囲まれた部分の面積は$\frac{-\ \boxed{\ \ ツ\ \ }+\boxed{\ \ テト\ \ }\sqrt{\boxed{\ \ ナ\ \ }}}{\boxed{\ \ ニ\ \ }}$である。
2022慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{3}}$mを実数とし、関数$y=|x^2-5x+4|$のグラフをC、直線$y=mx$を$l$とする。
(1)グラフCと直線lの共有点の個数は
$\boxed{\ \ アイ\ \ } \lt m \lt \boxed{\ \ ウ\ \ }$のとき0個
$m=\boxed{\ \ エオ\ \ }$のとき1個
$m \lt \boxed{\ \ カキ\ \ },\ m=\boxed{\ \ ク\ \ }$,または$m \gt \boxed{\ \ ケ\ \ }$のとき2個
$m=\boxed{\ \ コ\ \ }$のとき3個
$\boxed{\ \ サ\ \ } \lt m \lt \boxed{\ \ シ\ \ }$のとき4個
以下、グラフCと直線lの共有点の個数が3個の場合を考え、
グラフCと直線lの共有点を、x座標が小さい順にP,Q,Rとする。
(2)3点P,Q,Rのx座標は、順に$\boxed{\ \ ス\ \ }-\sqrt{\boxed{\ \ セ\ \ }},\ \boxed{\ \ ソ\ \ },\ \boxed{\ \ タ\ \ }+\sqrt{\boxed{\ \ チ\ \ }}$である。
(3)グラフCと線分QRで囲まれた部分の面積は$\frac{-\ \boxed{\ \ ツ\ \ }+\boxed{\ \ テト\ \ }\sqrt{\boxed{\ \ ナ\ \ }}}{\boxed{\ \ ニ\ \ }}$である。
2022慶應義塾大学商学部過去問
【中学生から理解できる!】三角比(さんかくひ)[ エッセンシャル版 ]:~全国入試問題解法

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
三角比に関して解説していきます.
この動画を見る
三角比に関して解説していきます.
5乗数を平方の和で
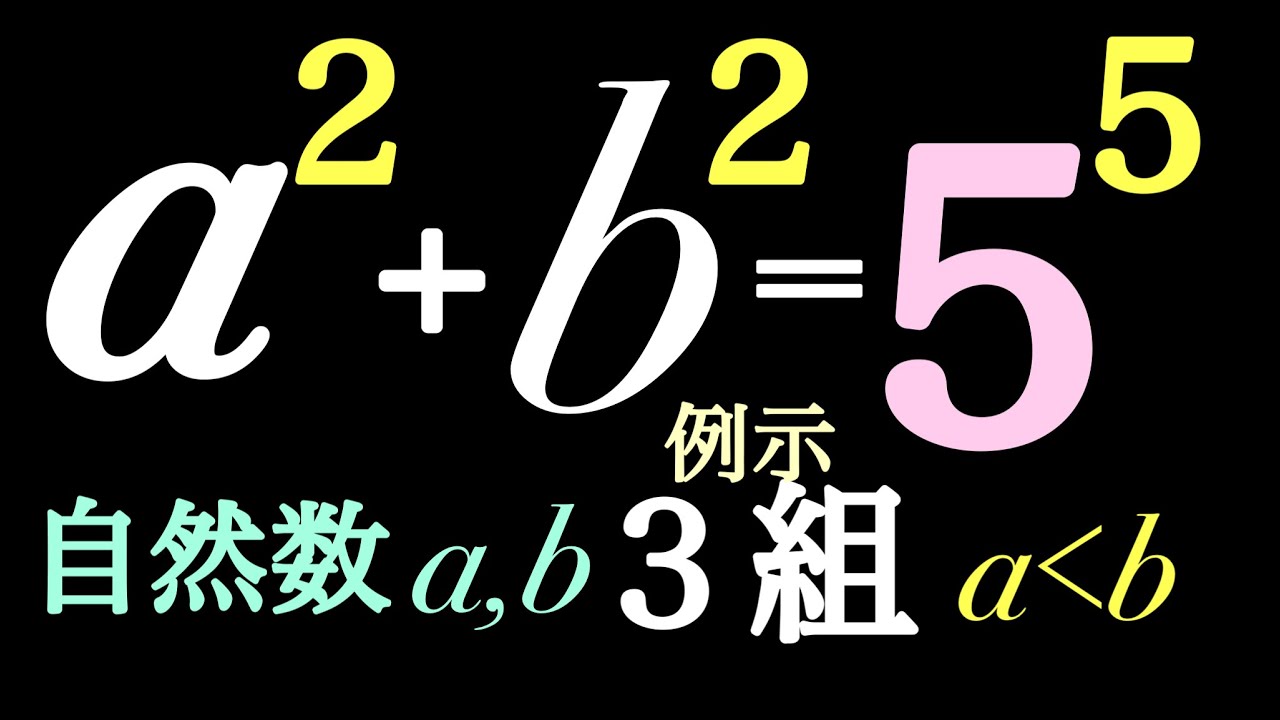
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a^2+b^2=5^5$,$a\lt b$
自然数$(a,b)$を3組例示せよ.
この動画を見る
$a^2+b^2=5^5$,$a\lt b$
自然数$(a,b)$を3組例示せよ.
福田の数学〜慶應義塾大学2022年商学部第1問(1)〜倍数の個数を数える

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(1)1から1000までの整数のうち、2,3,5の少なくとも2つで割り切れる数
は$\boxed{\ \ アイウ\ \ }$個あり、2,3,5の少なくとも1つで割り切れ、
かつ6で割り切れない数は$\boxed{\ \ エオカ\ \ }$個ある。
2022慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{1}}$(1)1から1000までの整数のうち、2,3,5の少なくとも2つで割り切れる数
は$\boxed{\ \ アイウ\ \ }$個あり、2,3,5の少なくとも1つで割り切れ、
かつ6で割り切れない数は$\boxed{\ \ エオカ\ \ }$個ある。
2022慶應義塾大学商学部過去問
ただの計算問題

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt{101^2+101^2・102^2+102^2}$
これを計算せよ.
この動画を見る
$ \sqrt{101^2+101^2・102^2+102^2}$
これを計算せよ.
福田の数学〜慶應義塾大学2022年経済学部第5問〜指数対数の性質と格子点と2次関数の最大

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{5}}$aを2以上の整数、pを整数とし、$s=2^{2p+1}$とおく。実数$x,y$が等式
$2^{a+1}\log_23^x+2x\log_2(\frac{1}{3})^x=\log_s9^y$
を満たすとき、yをxの関数として表したものを$y=f(x)$とする。
(1)対数の記号を使わずに、$f(x)$を$a,p$およびxを用いて表せ。
(2)$a=2,\ p=0$とする。このとき、$n \leqq f(m)$を満たし、かつ、$m+n$が正となる
ような整数の組(m,n)の個数を求めよ。
(3)$y=f(x)(0 \leqq x \leqq 2^{a+1})$の最大値が$2^{3a}$以下となるような整数pの
最大値と最小値を、それぞれaを用いて表せ。
2022慶應義塾大学経済学部過去問
この動画を見る
${\Large\boxed{5}}$aを2以上の整数、pを整数とし、$s=2^{2p+1}$とおく。実数$x,y$が等式
$2^{a+1}\log_23^x+2x\log_2(\frac{1}{3})^x=\log_s9^y$
を満たすとき、yをxの関数として表したものを$y=f(x)$とする。
(1)対数の記号を使わずに、$f(x)$を$a,p$およびxを用いて表せ。
(2)$a=2,\ p=0$とする。このとき、$n \leqq f(m)$を満たし、かつ、$m+n$が正となる
ような整数の組(m,n)の個数を求めよ。
(3)$y=f(x)(0 \leqq x \leqq 2^{a+1})$の最大値が$2^{3a}$以下となるような整数pの
最大値と最小値を、それぞれaを用いて表せ。
2022慶應義塾大学経済学部過去問
阪大の証明問題!解けますか?【数学 入試問題】【大阪大学 理系】

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n$を2以上の自然数とする。三角形$ABC$において,辺$AB$の長さを$c$,辺$CA$の長さを$b$で表す。$ \angle ACB=n \angle ABC$であるとき,$ c<nb $を示せ。
大阪大理系過去問
この動画を見る
$n$を2以上の自然数とする。三角形$ABC$において,辺$AB$の長さを$c$,辺$CA$の長さを$b$で表す。$ \angle ACB=n \angle ABC$であるとき,$ c<nb $を示せ。
大阪大理系過去問
正しいか、正しくないか

阪大の証明問題!ぜひとも取りたい問題【数学 入試問題】【大阪大学 文系】

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
三角形$ABC$において,辺$AB$の長さを$c$,辺$CA$の長さを$b$で表す。
$\angle ACB=3\angle ABC$であるとき,$c<3b$を示せ。
大阪大過去問
この動画を見る
三角形$ABC$において,辺$AB$の長さを$c$,辺$CA$の長さを$b$で表す。
$\angle ACB=3\angle ABC$であるとき,$c<3b$を示せ。
大阪大過去問
福田の数学〜慶應義塾大学2022年経済学部第3問〜データの分析と条件付き確率

単元:
#数Ⅰ#数A#大学入試過去問(数学)#場合の数と確率#データの分析#データの分析#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$xの関数が印刷されているカード25枚が1つの袋に入っている。
その内訳は、11枚に$1-3x$、9枚に$1-2x$、4枚に$1-2x+2x^2$、1枚に$1-3x+5x^2$である。
この袋からカードを1枚取り出し、印刷されている関数を記録してから袋に戻すことを
100回繰り返したところ、記録の内訳は$1-3x$が46回、$1-2x$が35回、$1-2x+2x^2$が15回、
$1-3x+5x^2$が4回であった。
(1)記録された関数の実数xにおける値を$a_1,a_2,\ldots,a_{100}$とおく。
$a_1,a_2,\ldots,a_{100}$の平均値は、xの値を定めるとそれに対応して値が定まるので、
xの関数である。この関数は$x=\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$のとき最小となり、その値は$-\frac{\boxed{\ \ ウエ\ \ }}{\boxed{\ \ オ\ \ }}$である。
(2)記録された関数の$x=0$から$x=1$までの定積分を$b_1,b_2,\ldots,b_{100}$とおく。
$b_1,b_2,\ldots,b_{100}$の平均値は$-\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キク\ \ }}$であり、
分散は$\frac{\boxed{\ \ ケコ\ \ }}{\boxed{\ \ サシ\ \ }}$である。
また、記録された関数の$x=1$における値を$c_1,c_2,\ldots,c_{100}$とおくとき、
100個のデータの組$(b_1,c_1),(b_2,c_2),\ldots,(b_{100},c_{100})$の共分散は$\frac{\boxed{\ \ スセ\ \ }}{\boxed{\ \ ソタ\ \ }}$である。
(3)カードがすべて袋に入った状態から1枚取り出したとき、印刷されている
関数の$x=1$における値が負である条件の下で、その関数の0から1までの定積分
が負である条件つき確率は$\frac{\boxed{\ \ チツ\ \ }}{\boxed{\ \ テト\ \ }}$である。
2022慶應義塾大学経済学部過去問
この動画を見る
${\Large\boxed{3}}$xの関数が印刷されているカード25枚が1つの袋に入っている。
その内訳は、11枚に$1-3x$、9枚に$1-2x$、4枚に$1-2x+2x^2$、1枚に$1-3x+5x^2$である。
この袋からカードを1枚取り出し、印刷されている関数を記録してから袋に戻すことを
100回繰り返したところ、記録の内訳は$1-3x$が46回、$1-2x$が35回、$1-2x+2x^2$が15回、
$1-3x+5x^2$が4回であった。
(1)記録された関数の実数xにおける値を$a_1,a_2,\ldots,a_{100}$とおく。
$a_1,a_2,\ldots,a_{100}$の平均値は、xの値を定めるとそれに対応して値が定まるので、
xの関数である。この関数は$x=\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$のとき最小となり、その値は$-\frac{\boxed{\ \ ウエ\ \ }}{\boxed{\ \ オ\ \ }}$である。
(2)記録された関数の$x=0$から$x=1$までの定積分を$b_1,b_2,\ldots,b_{100}$とおく。
$b_1,b_2,\ldots,b_{100}$の平均値は$-\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キク\ \ }}$であり、
分散は$\frac{\boxed{\ \ ケコ\ \ }}{\boxed{\ \ サシ\ \ }}$である。
また、記録された関数の$x=1$における値を$c_1,c_2,\ldots,c_{100}$とおくとき、
100個のデータの組$(b_1,c_1),(b_2,c_2),\ldots,(b_{100},c_{100})$の共分散は$\frac{\boxed{\ \ スセ\ \ }}{\boxed{\ \ ソタ\ \ }}$である。
(3)カードがすべて袋に入った状態から1枚取り出したとき、印刷されている
関数の$x=1$における値が負である条件の下で、その関数の0から1までの定積分
が負である条件つき確率は$\frac{\boxed{\ \ チツ\ \ }}{\boxed{\ \ テト\ \ }}$である。
2022慶應義塾大学経済学部過去問
式の値 筑波大

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
実数a,b,c,dが4つの等式
$a^2+b^2 = 1$ , $c^2+d^2 = 1$ ,
$ac +bd = 0$ , $ad +bc = 0 $を満たすとき
積abcdを求めよ
筑波大学
この動画を見る
実数a,b,c,dが4つの等式
$a^2+b^2 = 1$ , $c^2+d^2 = 1$ ,
$ac +bd = 0$ , $ad +bc = 0 $を満たすとき
積abcdを求めよ
筑波大学
福田の数学〜慶應義塾大学2022年経済学部第1問〜円に外接する四角形の性質

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
座標平面上の四角形ABCDは以下の条件を満たすとする。
$(\textrm{a})$頂点Aの座標は(-1,-1)である。
$(\textrm{b})$四角形の各辺は原点を中心とする半径1の円と接する。
$(\textrm{c})$$\angle BCD$は直角である。
また、辺ABの長さをlとし、$\angle ABC=\theta$とする。
(1)$\angle BAD=\frac{\pi}{\boxed{\ \ ア\ \ }}$である。
(2)辺CDの長さが$\frac{5}{3}$であるとき、$l=\frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }},\ \tan\theta=\frac{\boxed{\ \ エオ\ \ }}{\boxed{\ \ カ\ \ }}$である。
(3)$\theta$は鋭角とする。四角形ABCDの面積が6であるとき、$l=\boxed{\ \ キ\ \ }+\sqrt{\boxed{\ \ ク\ \ }}$ ,
$\theta = \frac{\pi}{\boxed{\ \ ケ\ \ }}$である。
2022慶應義塾大学経済学部過去問
この動画を見る
座標平面上の四角形ABCDは以下の条件を満たすとする。
$(\textrm{a})$頂点Aの座標は(-1,-1)である。
$(\textrm{b})$四角形の各辺は原点を中心とする半径1の円と接する。
$(\textrm{c})$$\angle BCD$は直角である。
また、辺ABの長さをlとし、$\angle ABC=\theta$とする。
(1)$\angle BAD=\frac{\pi}{\boxed{\ \ ア\ \ }}$である。
(2)辺CDの長さが$\frac{5}{3}$であるとき、$l=\frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }},\ \tan\theta=\frac{\boxed{\ \ エオ\ \ }}{\boxed{\ \ カ\ \ }}$である。
(3)$\theta$は鋭角とする。四角形ABCDの面積が6であるとき、$l=\boxed{\ \ キ\ \ }+\sqrt{\boxed{\ \ ク\ \ }}$ ,
$\theta = \frac{\pi}{\boxed{\ \ ケ\ \ }}$である。
2022慶應義塾大学経済学部過去問
破れたページは何ページ目?

単元:
#数Ⅰ#数と式#2次関数#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1枚だけページが破れた本があります。
破れていないページの番号を合計すると15000になる
破れたページは何ページ目ですか?
この動画を見る
1枚だけページが破れた本があります。
破れていないページの番号を合計すると15000になる
破れたページは何ページ目ですか?
【無理数とは!】平方根(有理数と無理数)後編:教科書順で内容確認~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
平方根(有理数と無理数)に関して解説していきます.
この動画を見る
平方根(有理数と無理数)に関して解説していきます.
よく出る問題!放物線と直線が接するということは?【数学 入試問題】【京都大学】

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次関数とグラフ#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
放物線$y=ax^2+bx+c$が3直線$y=x,y=2x-1,y=3x-3$のすべてと接するとき、$a,b,c$の値を求めよ。
京都大過去問
この動画を見る
放物線$y=ax^2+bx+c$が3直線$y=x,y=2x-1,y=3x-3$のすべてと接するとき、$a,b,c$の値を求めよ。
京都大過去問
4次式の因数分解

京大の三角比!気づければ簡単!【数学 入試問題】【京都大学】

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$\alpha,\beta$が$a>0°,\beta>0°,\alpha+\beta<180°$かつ$sin^2\alpha+sin^2\beta=sin^2(\alpha+\beta)$を満たすとき、
$sin\alpha+sin\beta$の取りうる範囲を求めよ。
京都大過去問
この動画を見る
$\alpha,\beta$が$a>0°,\beta>0°,\alpha+\beta<180°$かつ$sin^2\alpha+sin^2\beta=sin^2(\alpha+\beta)$を満たすとき、
$sin\alpha+sin\beta$の取りうる範囲を求めよ。
京都大過去問
