図形の性質
図形の性質
空間図形 垂直について 簡単だけど大切です。
単元：
#数A#図形の性質#空間における垂直と平行と多面体（オイラーの法則）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
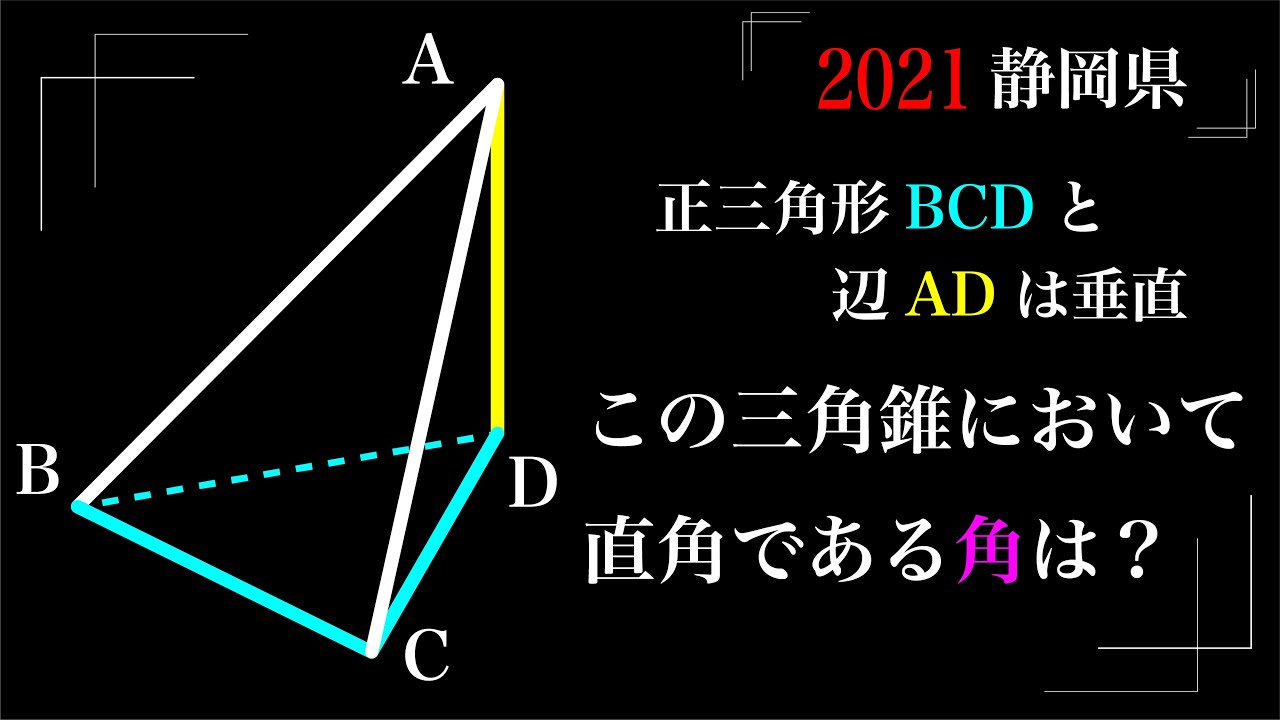
$AD⊥△BCD$
直角である角は？
＊図は動画内参照
2021静岡県
この動画を見る
$AD⊥△BCD$
直角である角は？
＊図は動画内参照
2021静岡県
円の中に円。巣鴨 図形
単元：
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
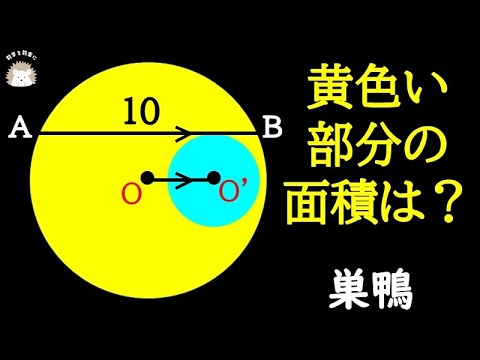
AB=10
斜線部の面積=?
＊図は動画内参照
巣鴨高等学校
この動画を見る
AB=10
斜線部の面積=?
＊図は動画内参照
巣鴨高等学校
気付けば一瞬！！ 図形
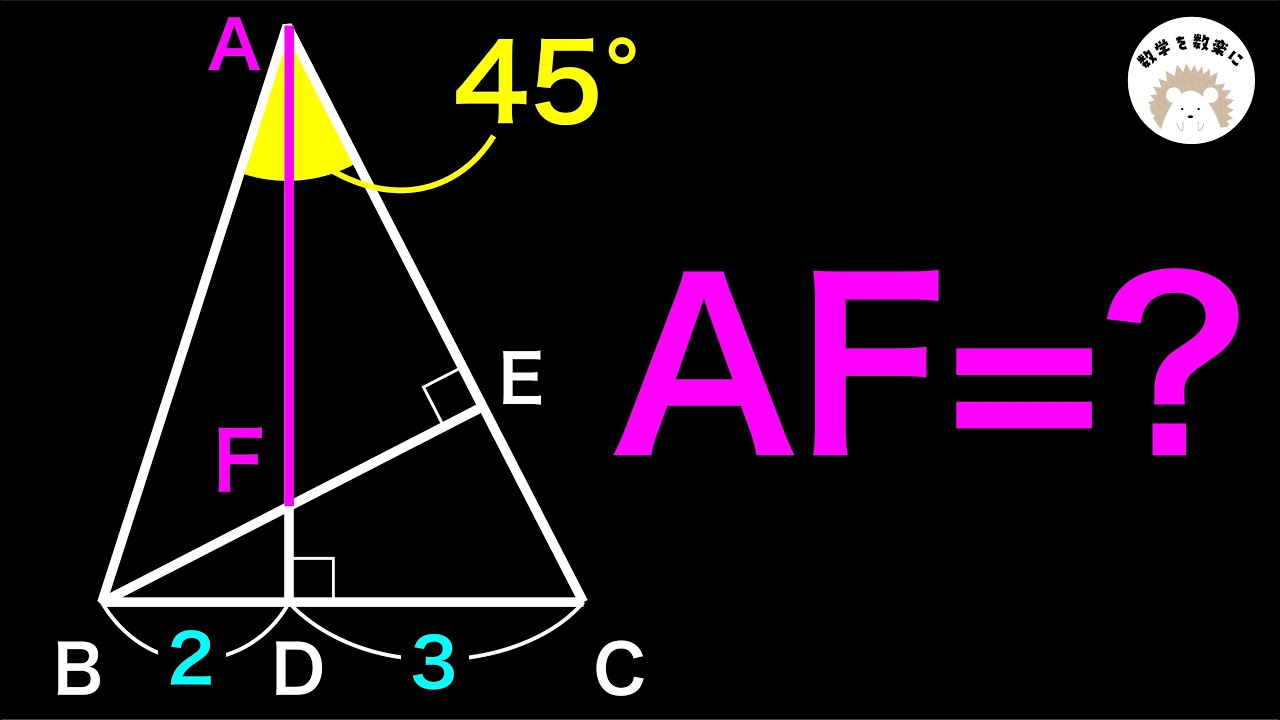
三角形の面積
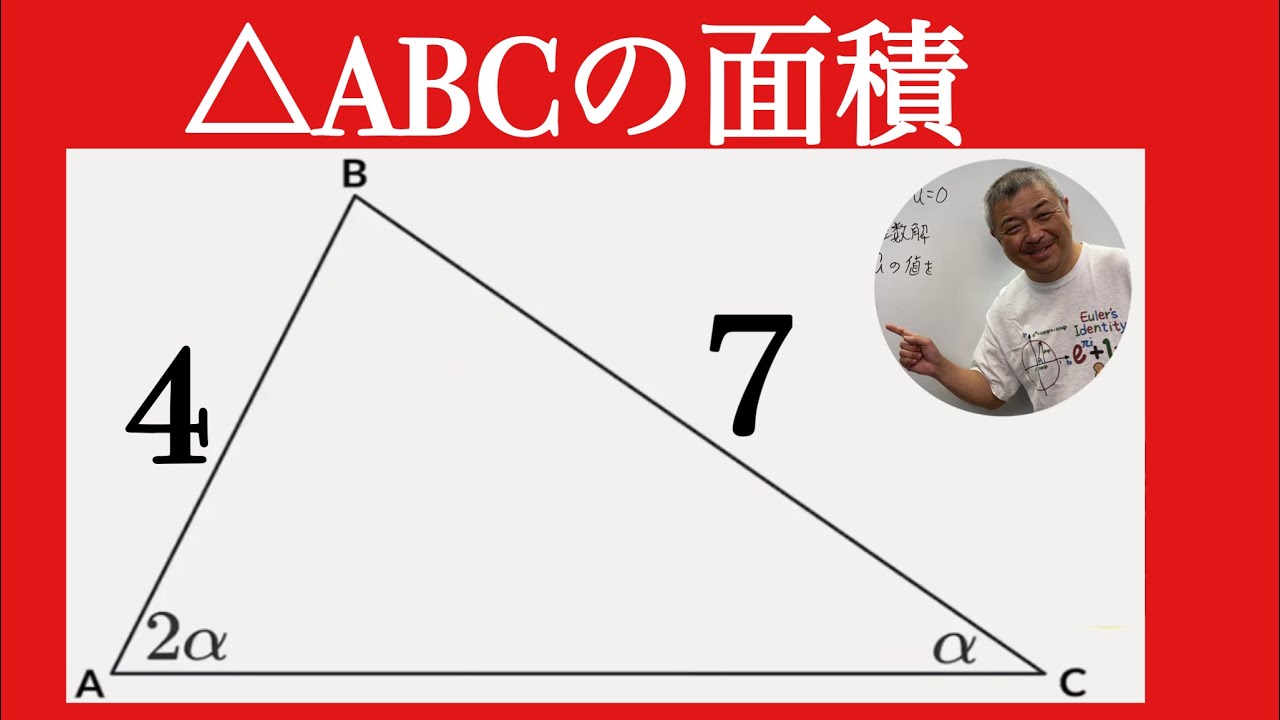
どう解く？
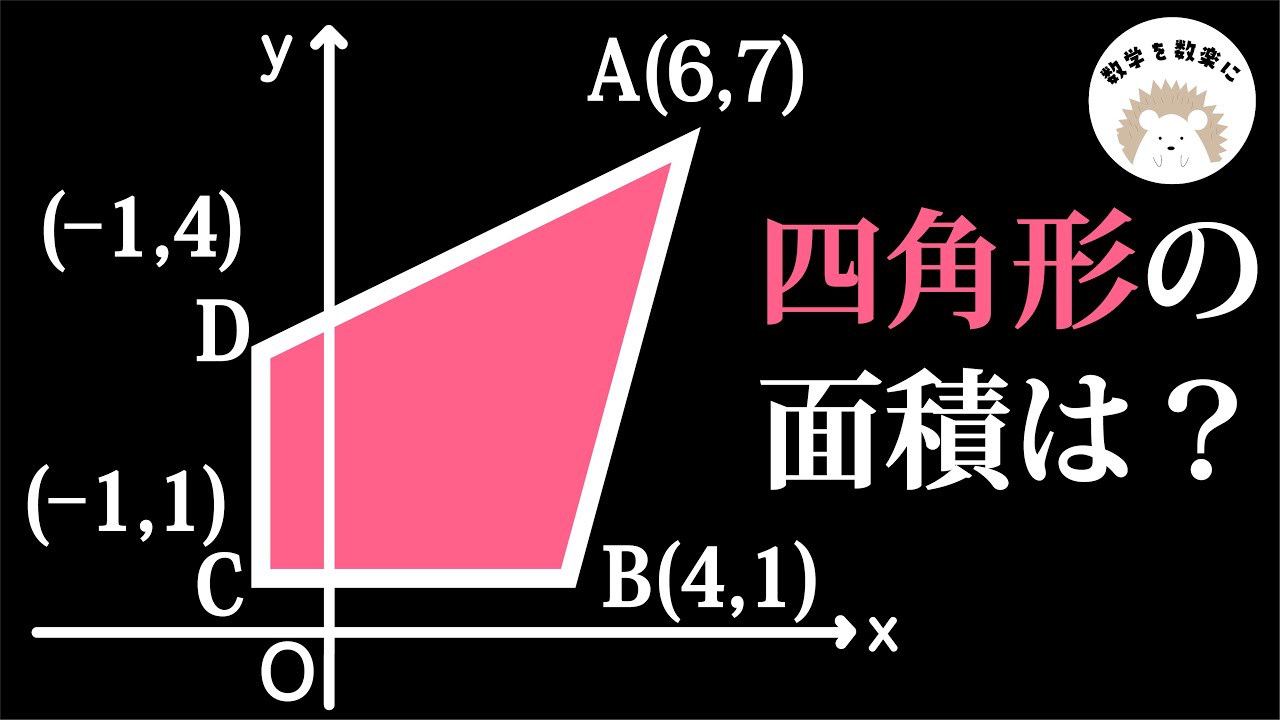
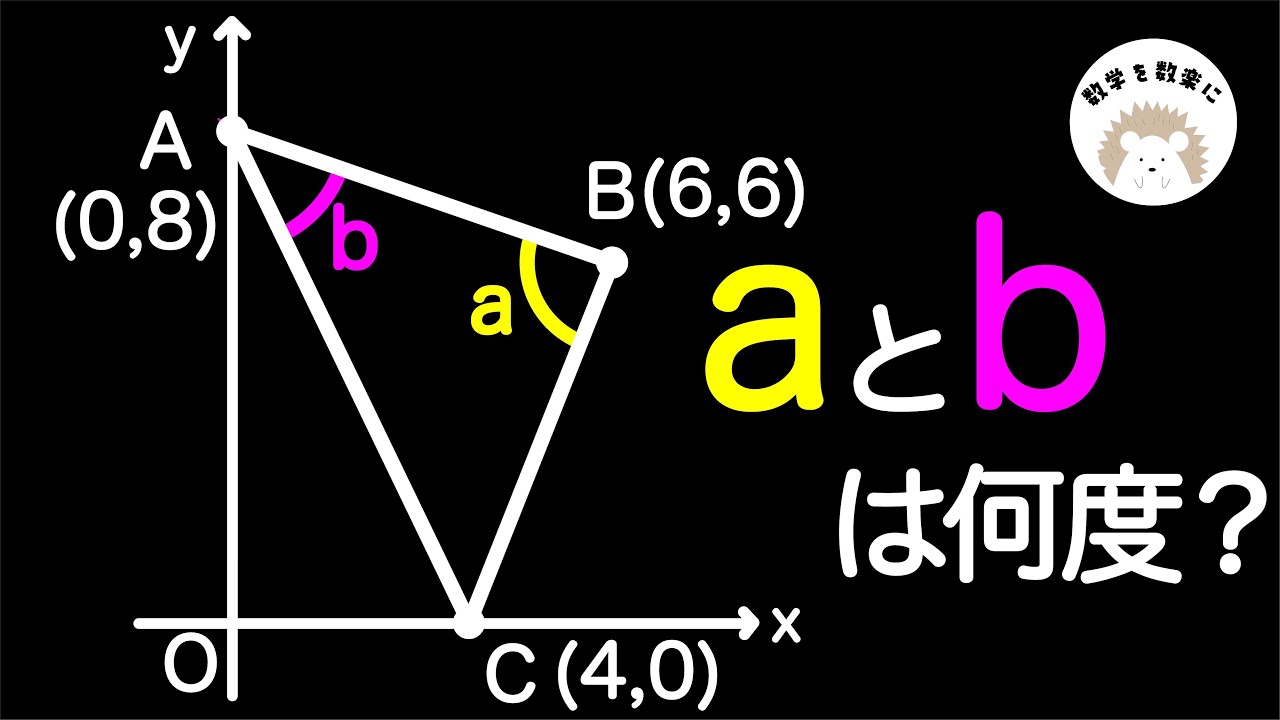
座標平面上の角度 2通りの解説
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$\angle a=?$
$\angle b=?$
＊図は動画内参照
この動画を見る
$\angle a=?$
$\angle b=?$
＊図は動画内参照
解き方無限大 高校入試 図形 円
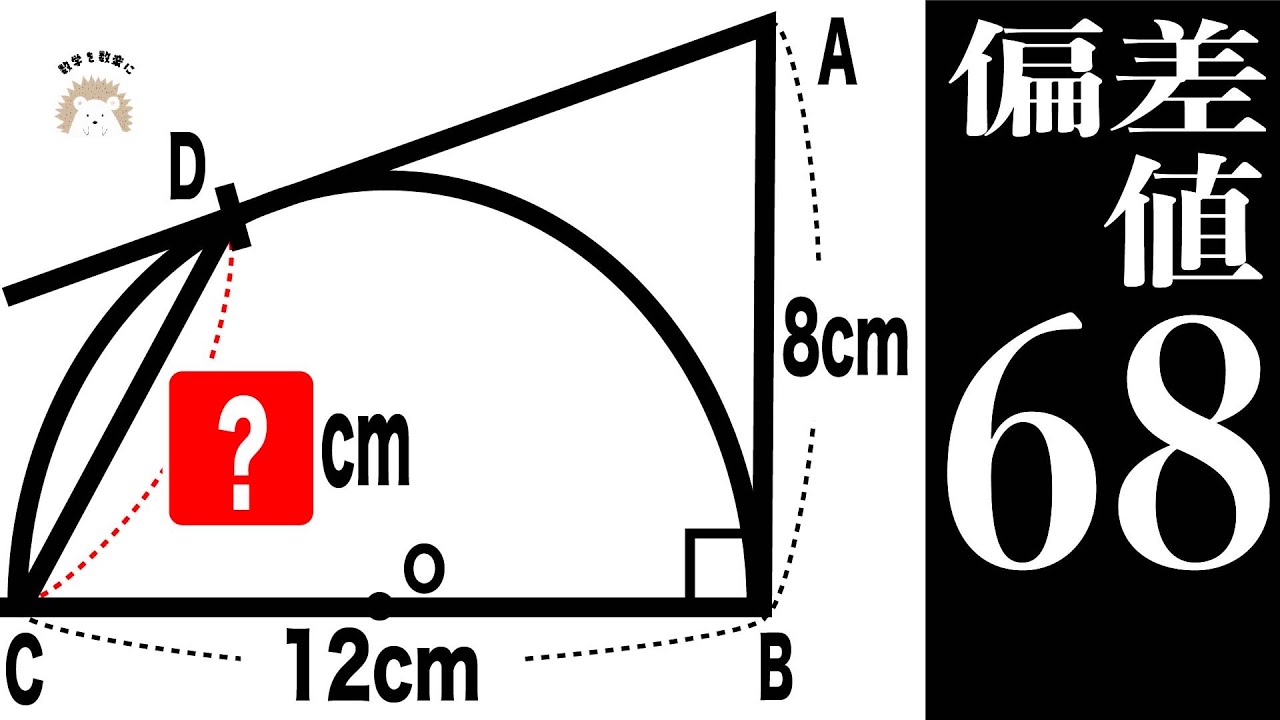
高校受験 図形問題
長方形と半円 気づけば一瞬！！
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
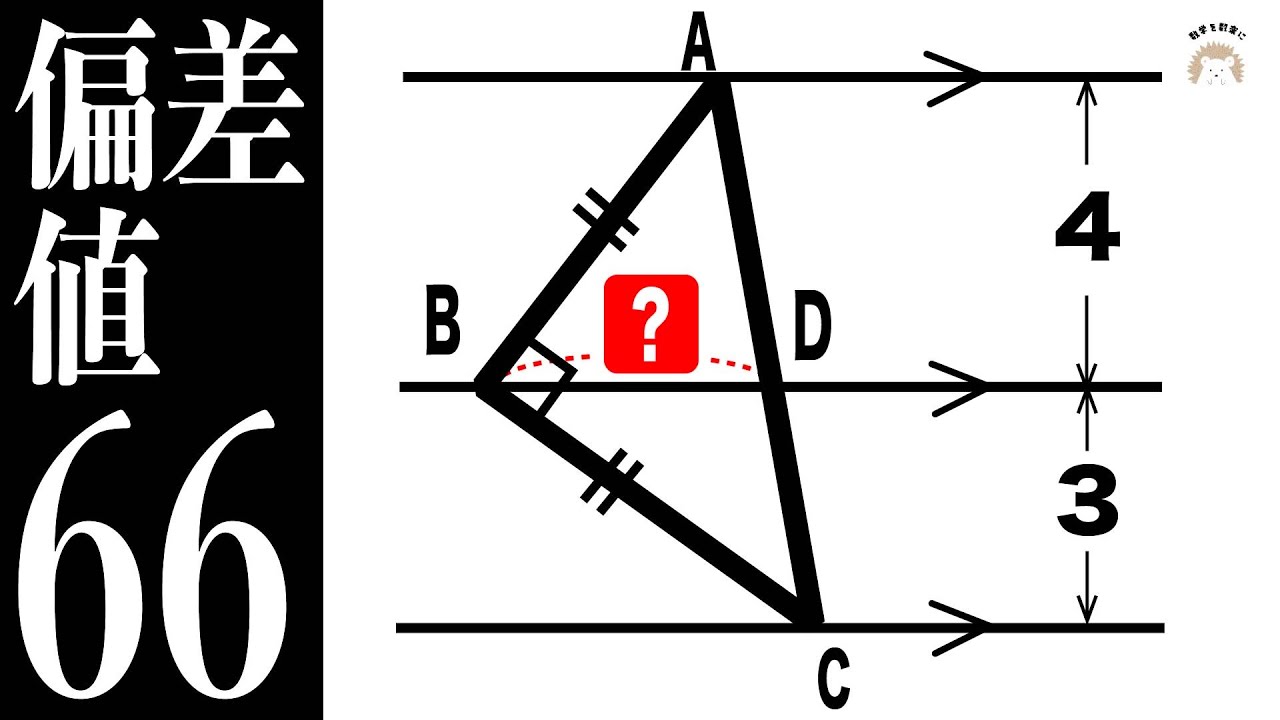
長方形と半円
斜線部の面積=?
＊図は動画内参照
この動画を見る
長方形と半円
斜線部の面積=?
＊図は動画内参照
面積
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
正方形
円の半径=5
赤線部の面積=?
＊図は動画内参照
この動画を見る
正方形
円の半径=5
赤線部の面積=?
＊図は動画内参照
円周角 暁
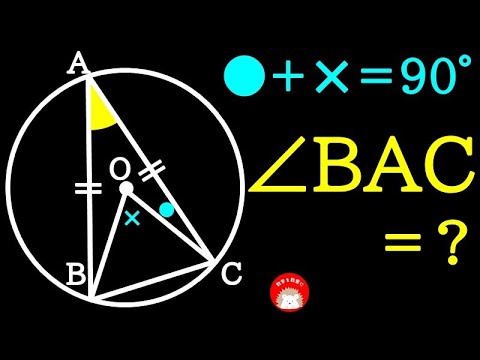
単元：
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
○+✖＝90°
$\angle BAC=?$
＊図は動画内参照
暁高等学校
この動画を見る
○+✖＝90°
$\angle BAC=?$
＊図は動画内参照
暁高等学校
〇〇に注目すれば一瞬！3通りで解説
角度を求める C
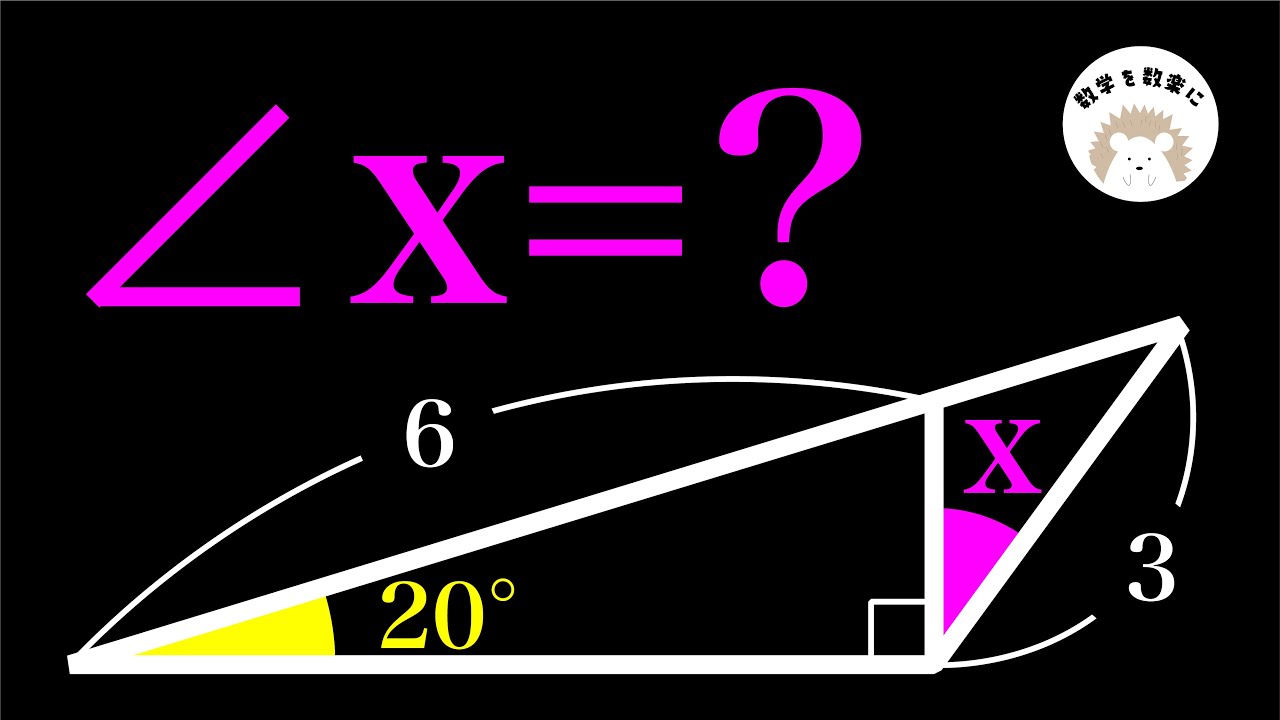
角度
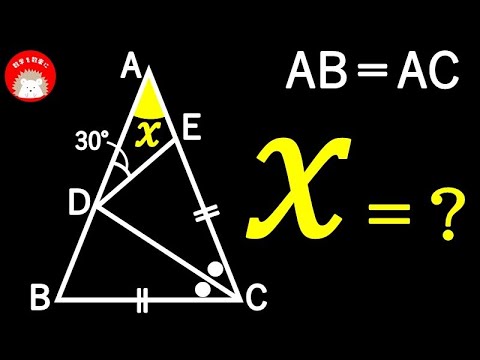
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
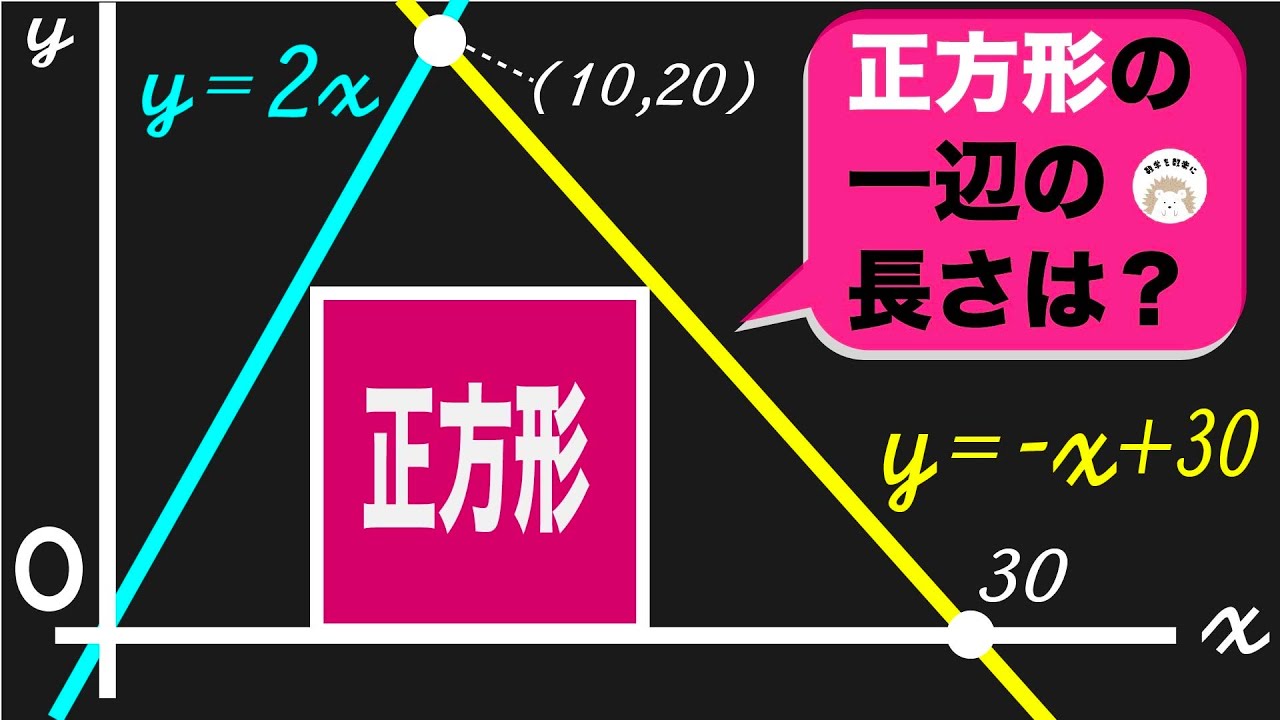
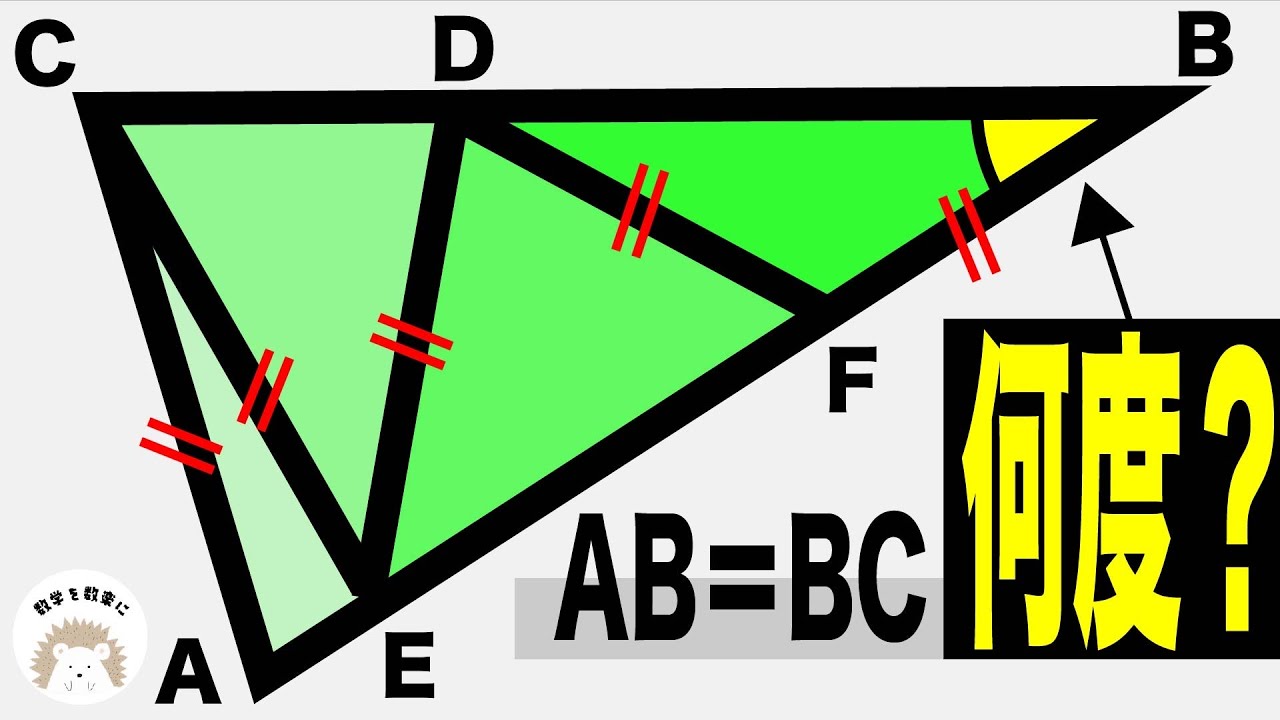
AB=AC
$\angle x= ?$
＊図は動画内参照
この動画を見る
AB=AC
$\angle x= ?$
＊図は動画内参照
図形と比 中学受験レベル
算数オリンピック 角度 C
単元：
#算数(中学受験)#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#平面図形#角度と面積#その他#算数オリンピック
指導講師：
数学を数楽に
問題文全文(内容文)：
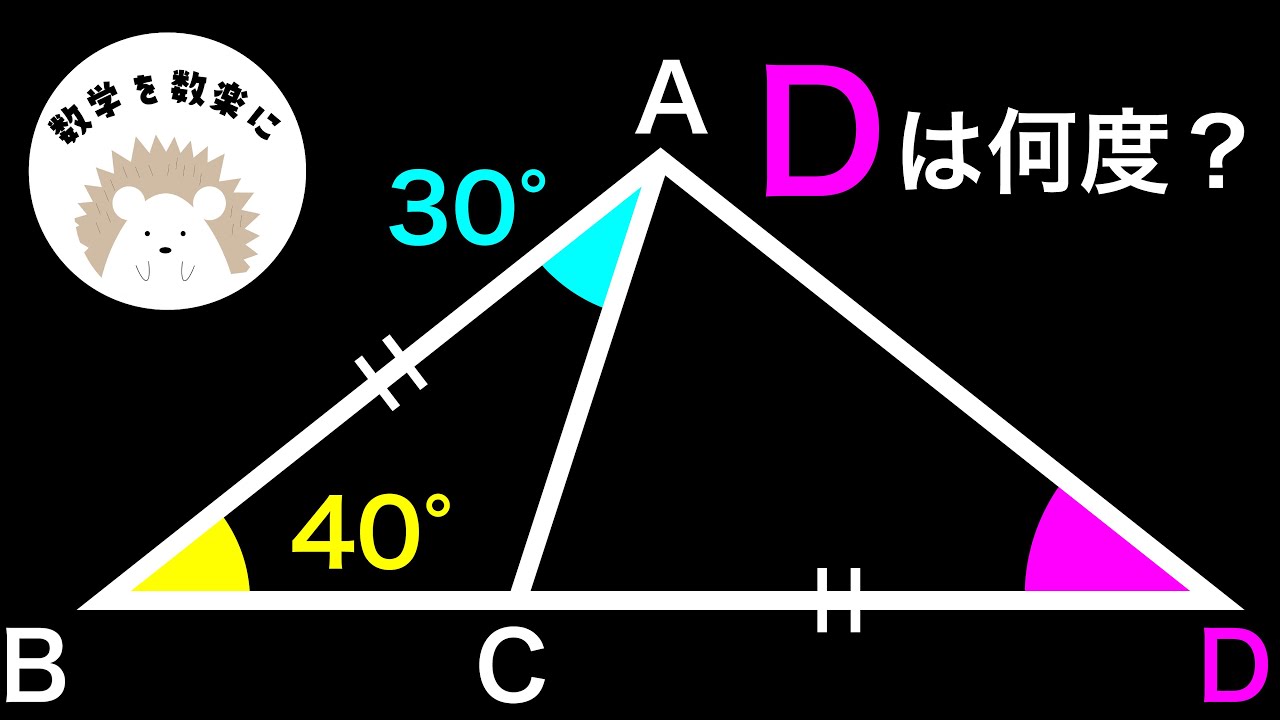
$\angle D=?$
＊図は動画内参照
算数オリンピック
この動画を見る
$\angle D=?$
＊図は動画内参照
算数オリンピック
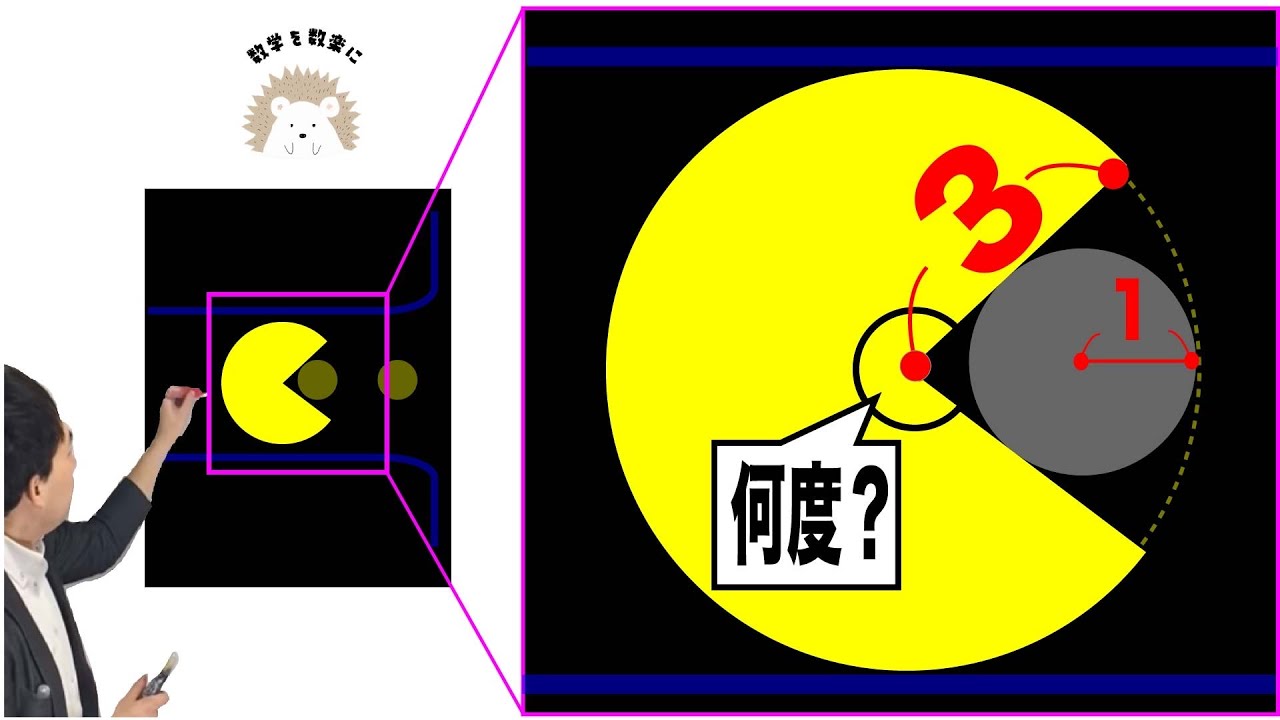
X＝❓ パックマン再び
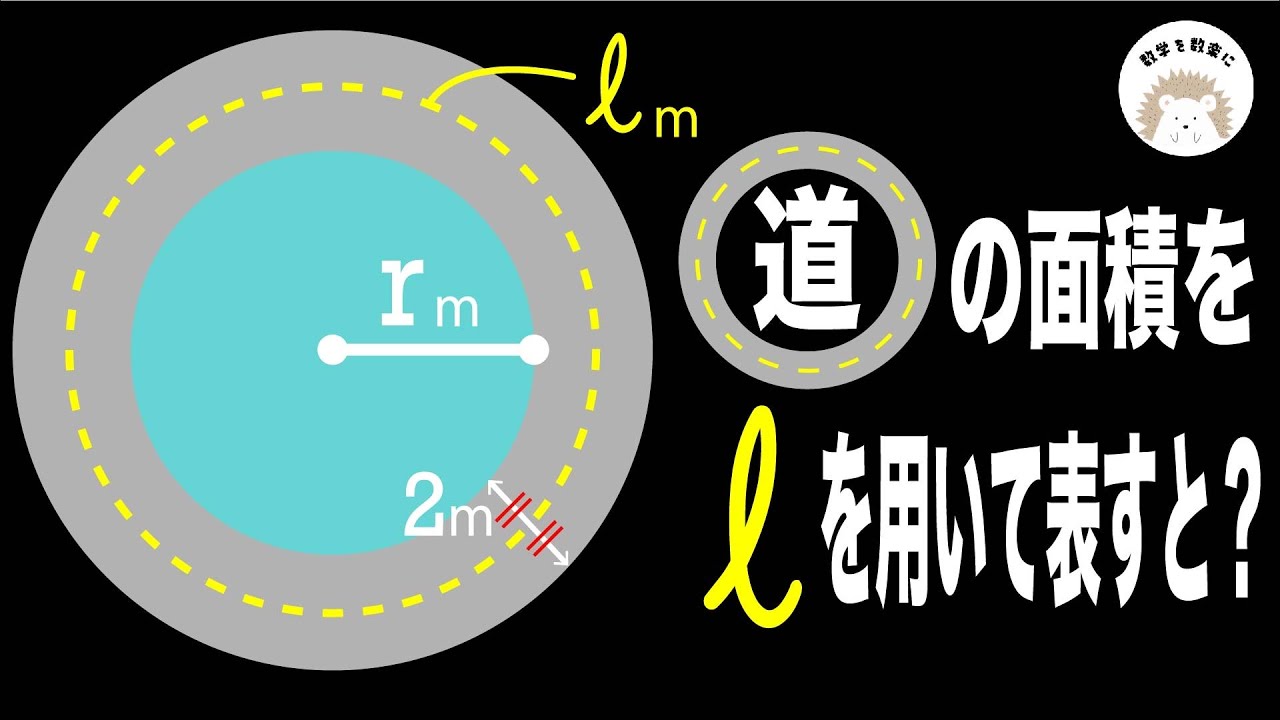
道の面積
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#平面図形#角度と面積#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
道の面積(s)をlを用いて表せ
＊図は動画内参照
この動画を見る
道の面積(s)をlを用いて表せ
＊図は動画内参照
正十二角形の中の三角形の個数
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#空間における垂直と平行と多面体（オイラーの法則）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
正十二角形の3つの頂点を結んでできる三角形の個数は$\boxed{ア}$コである。
そのうち
・2辺を共有する三角形は$\boxed{イ}$コ
・1辺を共有する三角形は$\boxed{ウ}$コ
・辺を共有しない三角形は$\boxed{エ}$コ
・直角三角形は$\boxed{オ}$コ
・正三角形は$\boxed{カ}$コ
・二等辺三角形は$\boxed{キ}$コ
ある。
＊図は動画内参照
この動画を見る
正十二角形の3つの頂点を結んでできる三角形の個数は$\boxed{ア}$コである。
そのうち
・2辺を共有する三角形は$\boxed{イ}$コ
・1辺を共有する三角形は$\boxed{ウ}$コ
・辺を共有しない三角形は$\boxed{エ}$コ
・直角三角形は$\boxed{オ}$コ
・正三角形は$\boxed{カ}$コ
・二等辺三角形は$\boxed{キ}$コ
ある。
＊図は動画内参照
数学「大学入試良問集」【6−6 外接球と四面体】を宇宙一わかりやすく
単元：
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用（正弦・余弦・面積）#内心・外心・重心とチェバ・メネラウス#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
$AB=5,BC=7,CA=8$および$OA=OB=OC=t$を満たす四面体$OABC$がある。
（1）$\angle BAC$を求めよ。
（2）$\triangle ABC$の外接円の半径を求めよ。
（3）4つの頂点$O,A,B,C$が同一球面上にあるとき、その球の半径が最小となるような実数$t$の値を求めよ。
この動画を見る
$AB=5,BC=7,CA=8$および$OA=OB=OC=t$を満たす四面体$OABC$がある。
（1）$\angle BAC$を求めよ。
（2）$\triangle ABC$の外接円の半径を求めよ。
（3）4つの頂点$O,A,B,C$が同一球面上にあるとき、その球の半径が最小となるような実数$t$の値を求めよ。
角度が出てないのに角度が求まる
数学「大学入試良問集」【6−5 母線の等しい四面体】を宇宙一わかりやすく
単元：
#数Ⅰ#数A#図形の性質#図形と計量#三角比（三角比・拡張・相互関係・単位円）#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
1辺の長さが2の正三角形$ABC$を底面とし、
$OA=OB=OC=2a(a \gt 1)$
である四面体$OABC$について、辺$AB$の中点を$M$とし、頂点$O$から直線$CM$に下した垂線を$OH$とする。
$\angle OMC=\theta$とするとき、次の各問いに答えよ。
（1）$\cos\theta$を$a$を用いて表せ。
（2）$OH$の長さを$a$を用いて表せ。
（3）$OH$の長さが$2\sqrt{ 3 }$になるときの$a$の値を求めよ。
この動画を見る
1辺の長さが2の正三角形$ABC$を底面とし、
$OA=OB=OC=2a(a \gt 1)$
である四面体$OABC$について、辺$AB$の中点を$M$とし、頂点$O$から直線$CM$に下した垂線を$OH$とする。
$\angle OMC=\theta$とするとき、次の各問いに答えよ。
（1）$\cos\theta$を$a$を用いて表せ。
（2）$OH$の長さを$a$を用いて表せ。
（3）$OH$の長さが$2\sqrt{ 3 }$になるときの$a$の値を求めよ。
数学「大学入試良問集」【6−4 メネラウス、方べきの定理】を宇宙一わかりやすく
単元：
#数A#大学入試過去問(数学)#図形の性質#内心・外心・重心とチェバ・メネラウス#方べきの定理と２つの円の関係#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
$\triangle ABC$に対し、点$P$辺$AB$の中点、点$Q$は辺$BC$上の$B,C$と異なる点、点$R$は直線$AQ$と直線$CP$との交点とする。
このとき、各問いに答えよ。
（1）
$a=\displaystyle \frac{CR}{RP},b=\displaystyle \frac{CQ}{QB}$とおくとき、$a$と$b$の関係式を求めよ。
（2）
$\triangle ABC$の外接円$O$と直線$CP$との点$C$以外の交点を$X$とする。
$AP=CR,CQ=QB$であるとき、$CR:RP:PX$を求めよ。
この動画を見る
$\triangle ABC$に対し、点$P$辺$AB$の中点、点$Q$は辺$BC$上の$B,C$と異なる点、点$R$は直線$AQ$と直線$CP$との交点とする。
このとき、各問いに答えよ。
（1）
$a=\displaystyle \frac{CR}{RP},b=\displaystyle \frac{CQ}{QB}$とおくとき、$a$と$b$の関係式を求めよ。
（2）
$\triangle ABC$の外接円$O$と直線$CP$との点$C$以外の交点を$X$とする。
$AP=CR,CQ=QB$であるとき、$CR:RP:PX$を求めよ。
数学「大学入試良問集」【6−3 内接四角形】を宇宙一わかりやすく
単元：
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用（正弦・余弦・面積）#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
四角形$ABCD$が、半径$\displaystyle \frac{65}{8}$の円に内接している。
この四角形の週の長さが$44$で、辺$BC$と辺$CD$の長さがいずれも$13$であるとき、残りの2辺$AB$と$DA$の長さを求めよ。
この動画を見る
四角形$ABCD$が、半径$\displaystyle \frac{65}{8}$の円に内接している。
この四角形の週の長さが$44$で、辺$BC$と辺$CD$の長さがいずれも$13$であるとき、残りの2辺$AB$と$DA$の長さを求めよ。
小学生解き方 中学生の解き方
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
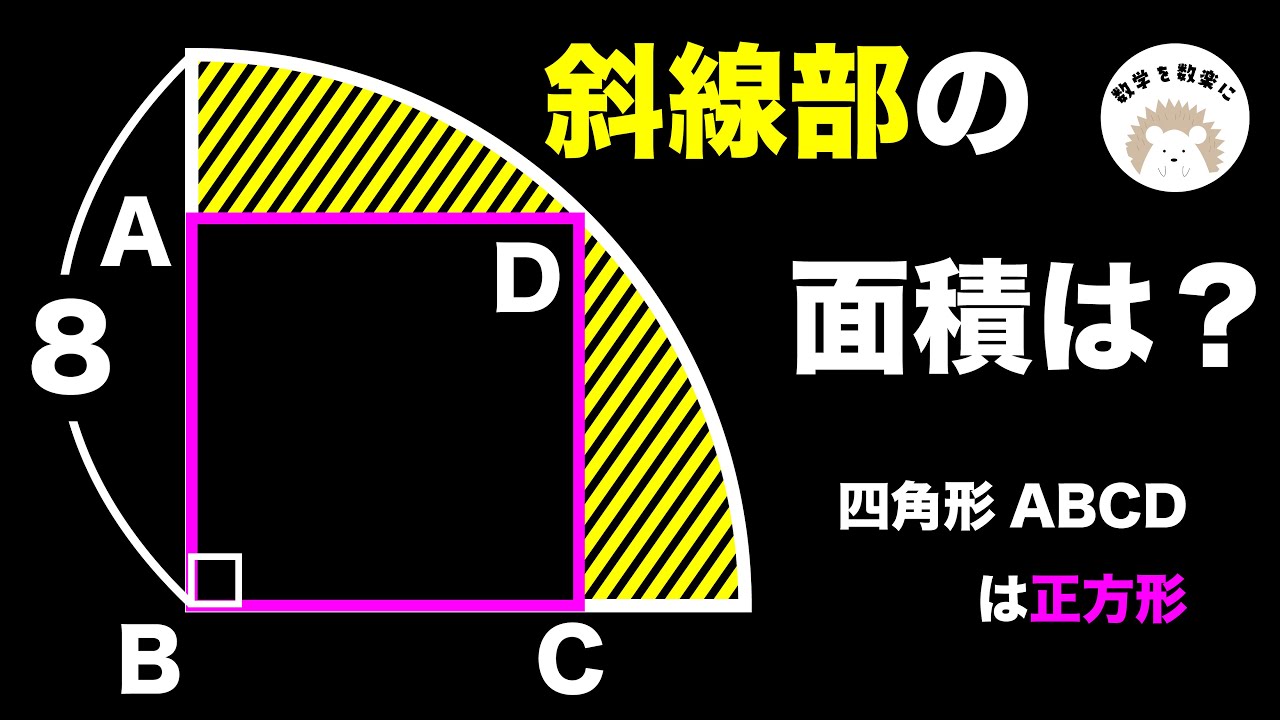
四角形ABCDは正方形
斜線部の面積=?
＊図は動画内参照
この動画を見る
四角形ABCDは正方形
斜線部の面積=?
＊図は動画内参照
太陽と黒点
単元：
#数A#図形の性質#方べきの定理と２つの円の関係#平面図形#角度と面積#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
2つの円の半径の和=47,2つの円の半径の差=43のとき
斜線部の面積=?
＊図は動画内参照
この動画を見る
2つの円の半径の和=47,2つの円の半径の差=43のとき
斜線部の面積=?
＊図は動画内参照
内心 こんなところに黄金比が
練習問題24 兵庫県教採練習問題 14番 面積
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{14}$
$c:y=x\sin x \ (0\leqq x\leqq 2\pi)$
第4象限にある$C$上の点の接線$\ell$は原点を通る.
$c$と$\ell$で囲まれた面積$S$を求めよ.
この動画を見る
$\boxed{14}$
$c:y=x\sin x \ (0\leqq x\leqq 2\pi)$
第4象限にある$C$上の点の接線$\ell$は原点を通る.
$c$と$\ell$で囲まれた面積$S$を求めよ.
気付くの難しめ 西大和学園2021
単元：
#数学(中学生)#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
a:b=?
＊図は動画内参照
西大和学園高等学校
この動画を見る
a:b=?
＊図は動画内参照
西大和学園高等学校
３つの並んだ合同な正三角形
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#平面図形#角度と面積#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
1つの正三角形の面積=18
斜線部の面積は?
＊図は動画内参照
この動画を見る
1つの正三角形の面積=18
斜線部の面積は?
＊図は動画内参照