 数A
数A
 数A
数A
【数検準2級】高校数学:数学検定準2級2次:問3

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学検定#数学検定準2級#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問3.次の問いに答えなさい。
(4) 右の図の四角形ABCDは平行四辺形です。また、点E、F、Gは辺ABを4等分する点で、点H、I、Jは辺CDを4等分する点です。
斜線部分の面積が10㎝²であるとき、四角形ABCDの面積を求めなさい。この問題は答えだけを書いてください。
この動画を見る
問3.次の問いに答えなさい。
(4) 右の図の四角形ABCDは平行四辺形です。また、点E、F、Gは辺ABを4等分する点で、点H、I、Jは辺CDを4等分する点です。
斜線部分の面積が10㎝²であるとき、四角形ABCDの面積を求めなさい。この問題は答えだけを書いてください。
整数問題!問題文でかなり範囲が絞られている!?さらに候補を絞り込もう!【一橋大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
nを2以上20以下の整数、kを1以上n-1以下の整数とする。
${}_{n+1} \mathrm{ C }_{k+1}$=$2({}_n \mathrm{ C }_{k-1}+{}_n \mathrm{ C }_{k+1})$
が成り立つような整数の組(n,k)を求めよ。
一橋大過去問
この動画を見る
nを2以上20以下の整数、kを1以上n-1以下の整数とする。
${}_{n+1} \mathrm{ C }_{k+1}$=$2({}_n \mathrm{ C }_{k-1}+{}_n \mathrm{ C }_{k+1})$
が成り立つような整数の組(n,k)を求めよ。
一橋大過去問
福田の数学〜慶應義塾大学2023年看護医療学部第2問(2)〜ルートが自然数になる条件

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ (2)$n$を自然数とする。$\sqrt{\frac{200}{\sqrt n}}$が自然数となるような$n$をすべて求めると$n$=$\boxed{\ \ サ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{2}$ (2)$n$を自然数とする。$\sqrt{\frac{200}{\sqrt n}}$が自然数となるような$n$をすべて求めると$n$=$\boxed{\ \ サ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
【公式より「思考」が大切!】整数:埼玉県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#数A#整数の性質#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \sqrt{\dfrac{540}{n}}$
整数となるような自然数$ n $は全部で何通りあるか.
埼玉県高校過去問
この動画を見る
$ \sqrt{\dfrac{540}{n}}$
整数となるような自然数$ n $は全部で何通りあるか.
埼玉県高校過去問
割った余り 愛知淑徳

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
自然数$m,n$が
$3(m+7)=5(n+11)$を満たすとき
$m$を5で割った余りを求めよ
愛知淑徳高等学校
この動画を見る
自然数$m,n$が
$3(m+7)=5(n+11)$を満たすとき
$m$を5で割った余りを求めよ
愛知淑徳高等学校
図形の性質 作図問題【TAKAHASHI名人がていねいに解説】

単元:
#数A#図形の性質#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
線分ABが与えられたとき, 線分ABを斜辺とし, $\angle BAC=60°$ である直角三角形ABC を作図せよ。
右の図のような円があり,その周上に点Aがある。
Aを頂点の1つとし、他の5つの頂点がいずれもこの円周上にあるような正六角形を作図せよ。
右の図のように,直線と円Oおよびその中心が与えられている。
直線lに平行な円Oの接線を作図せよ。
この動画を見る
線分ABが与えられたとき, 線分ABを斜辺とし, $\angle BAC=60°$ である直角三角形ABC を作図せよ。
右の図のような円があり,その周上に点Aがある。
Aを頂点の1つとし、他の5つの頂点がいずれもこの円周上にあるような正六角形を作図せよ。
右の図のように,直線と円Oおよびその中心が与えられている。
直線lに平行な円Oの接線を作図せよ。
図形の性質 方べきの定理【TAKAHASHI名人がていねいに解説】
単元:
#数A#図形の性質#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
■問題文
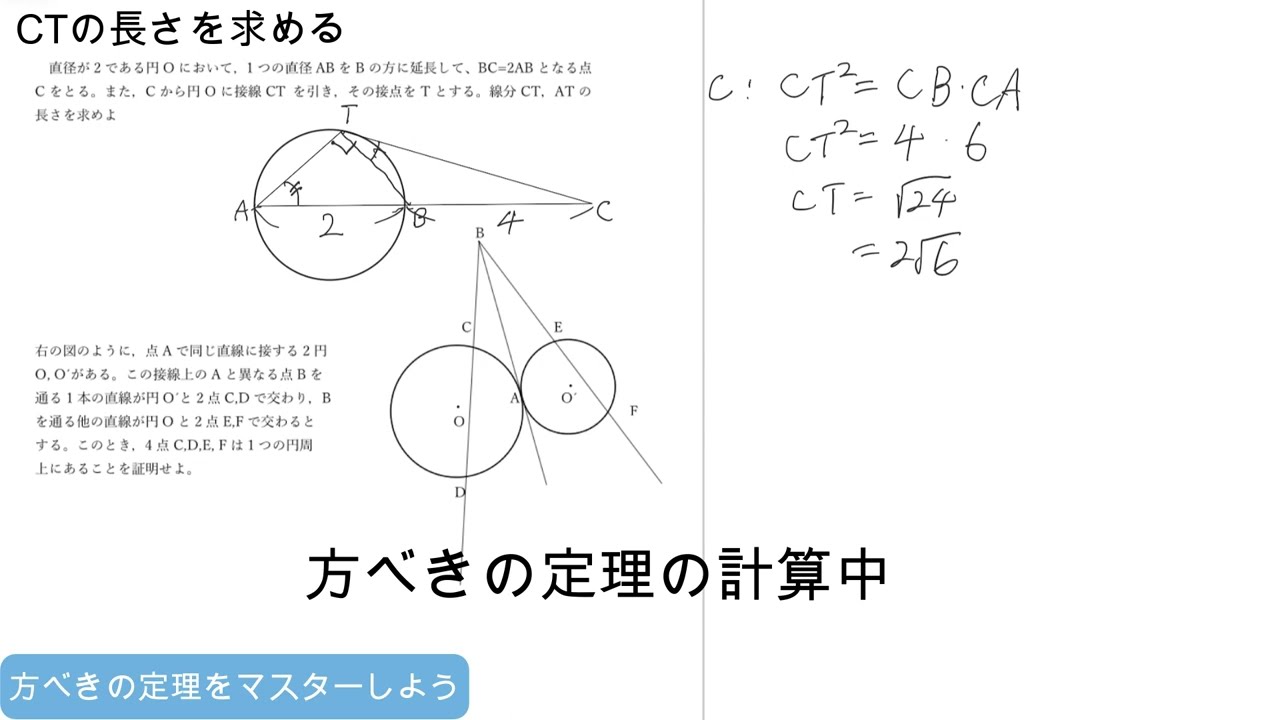
直径が2である円Oにおいて、1つの直径ABをBの方に延長して、BC=2ABとなる点Cをとる。また、Cから円Oに接線CTを引き、その接点をTとする。線分CT,ATの長さを求めよ。
右の図のように、点Aで同じ直線に接する2円O、O´がある。
この接線上のAと異なる点Bを通る1本の直線が円Oと2点C,Dで交わり, Bを通る他の直線が円 O′と2点E,Fで交わるとする。このとき, 4点 C, D, E, F は1つの円周上にあることを証明せよ。
この動画を見る
■問題文
直径が2である円Oにおいて、1つの直径ABをBの方に延長して、BC=2ABとなる点Cをとる。また、Cから円Oに接線CTを引き、その接点をTとする。線分CT,ATの長さを求めよ。
右の図のように、点Aで同じ直線に接する2円O、O´がある。
この接線上のAと異なる点Bを通る1本の直線が円Oと2点C,Dで交わり, Bを通る他の直線が円 O′と2点E,Fで交わるとする。このとき, 4点 C, D, E, F は1つの円周上にあることを証明せよ。
15度75度90度の直角三角形の比は受験生は覚えた方が良い。また、導けますか?

【1分で得意分野!】整数:精華女子高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
ある自然数を2乗して3引くところを間違えて2倍して3を引いたので
正しい答えより15小さくなった.ある自然数を求めよ.
精華女子高等学校過去問
この動画を見る
ある自然数を2乗して3引くところを間違えて2倍して3を引いたので
正しい答えより15小さくなった.ある自然数を求めよ.
精華女子高等学校過去問
場合の数と確率 確率基本①【教えて鈴木先生がていねいに解説】

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
A,B,C,D,E,F,G,Hの8文字を無造作に1列に並べるとき、次のようになる確率を求めよ。
(1)両端がA,Bである。
(2)A,Bが隣り合う。
(3)AはBより左に、BはCより左にある。
男子6人、女子2人がくじ引きで席を決めて円卓を囲んで座るとき、次のようになる確率を求めよ。
(1)女子2人が隣り合う。
(2)女子2人が向かい合う。
A,B,C,Dの4人がじゃんけんを1回するとき、次の確率を求めよ。
(1)Aだけが勝つ確率
(2)1人だけが勝つ確率
3つのさいころを同時に投げるとき、次のような目が出る確率を求めよ。
(1)目の積が150
(2)目の積が18
(3)目の積が135以上
この動画を見る
A,B,C,D,E,F,G,Hの8文字を無造作に1列に並べるとき、次のようになる確率を求めよ。
(1)両端がA,Bである。
(2)A,Bが隣り合う。
(3)AはBより左に、BはCより左にある。
男子6人、女子2人がくじ引きで席を決めて円卓を囲んで座るとき、次のようになる確率を求めよ。
(1)女子2人が隣り合う。
(2)女子2人が向かい合う。
A,B,C,Dの4人がじゃんけんを1回するとき、次の確率を求めよ。
(1)Aだけが勝つ確率
(2)1人だけが勝つ確率
3つのさいころを同時に投げるとき、次のような目が出る確率を求めよ。
(1)目の積が150
(2)目の積が18
(3)目の積が135以上
福田の数学〜慶應義塾大学2023年看護医療学部第1問(2)〜同じものを含む順列

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)k a n g o g a k u の9文字すべてを並べてできる文字列の種類は全部で$\boxed{\ \ ウ\ \ }$通りであり、このうち子音と母音が交互に並ぶものは$\boxed{\ \ エ\ \ }$通りである。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{1}$ (2)k a n g o g a k u の9文字すべてを並べてできる文字列の種類は全部で$\boxed{\ \ ウ\ \ }$通りであり、このうち子音と母音が交互に並ぶものは$\boxed{\ \ エ\ \ }$通りである。
2023慶應義塾大学看護医療学部過去問
思わぬ落とし穴 方程式を解け 拓殖大

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
方程式
$\frac{x}{x+1} + \frac{3x-1}{x^2-2x-3}=3$を解け
拓殖大学
この動画を見る
方程式
$\frac{x}{x+1} + \frac{3x-1}{x^2-2x-3}=3$を解け
拓殖大学
福田の数学〜慶應義塾大学2023年医学部第4問PART2〜円に内接する円の性質
単元:
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
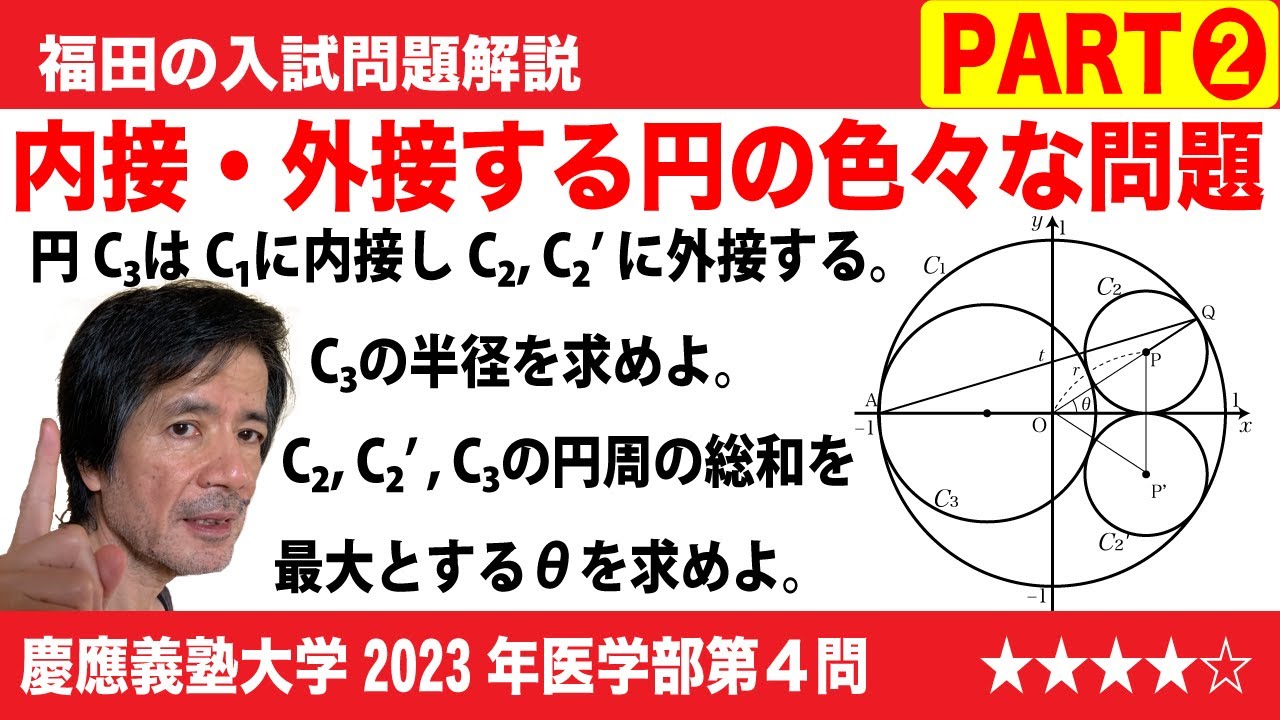
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年医学部第4問PART1〜円に内接する円の性質
単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#複素数平面#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#円と方程式#微分とその応用#複素数平面#図形への応用#微分法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
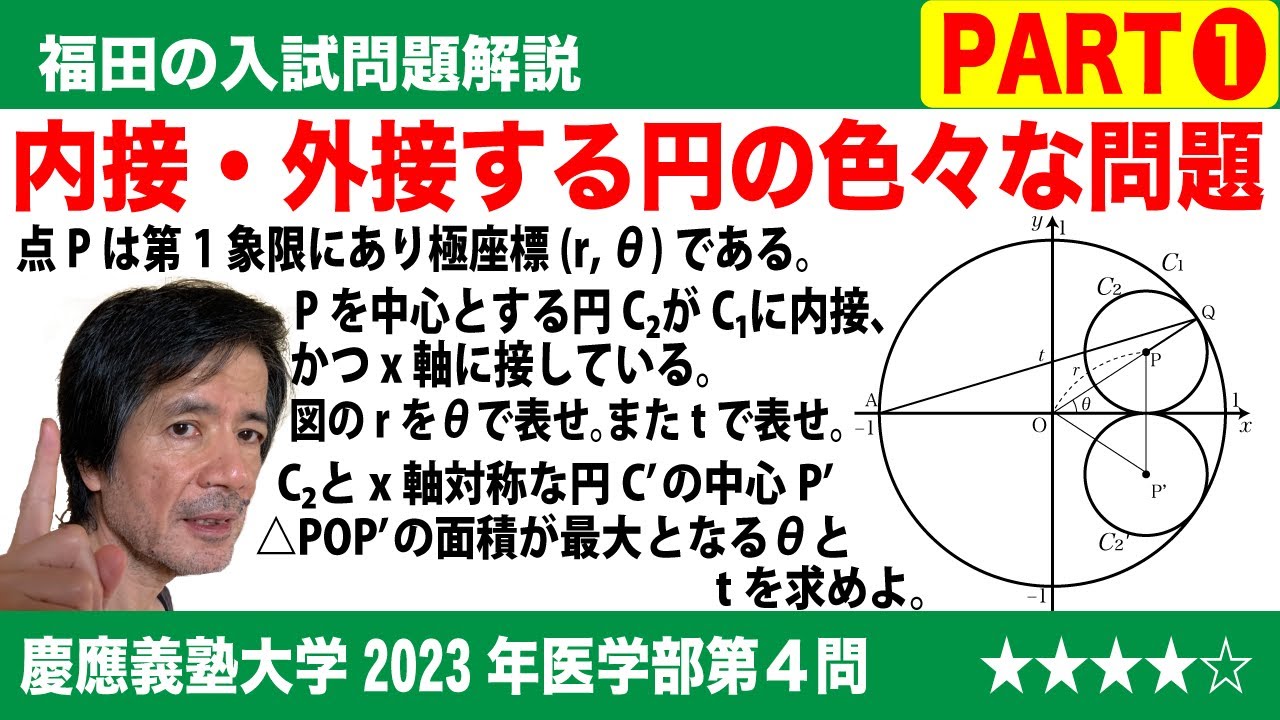
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
視聴者さんからの出題

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\stackrel{\huge\frown}{AP}$+$\stackrel{\huge\frown}{BQ}$ =?
*図は動画内参照
この動画を見る
$\stackrel{\huge\frown}{AP}$+$\stackrel{\huge\frown}{BQ}$ =?
*図は動画内参照
整数の性質 最小公倍数、最大公約数の基本① 【ゆう☆たろうがていねいに解説】

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
nは正の整数とする。次のようなnをすべて求めよ。
(1)nと36の最小公倍数が504
(2)nと48の最小公倍数が720
3つの自然数40,56,nの最大公約数が8,最小公倍数が1400であるとき,nをすべて求めよ。
aは自然数とする。a+2は6の倍数であり,a+6は8の倍数であるとき,a+14は24の倍数であることを証明せよ
この動画を見る
nは正の整数とする。次のようなnをすべて求めよ。
(1)nと36の最小公倍数が504
(2)nと48の最小公倍数が720
3つの自然数40,56,nの最大公約数が8,最小公倍数が1400であるとき,nをすべて求めよ。
aは自然数とする。a+2は6の倍数であり,a+6は8の倍数であるとき,a+14は24の倍数であることを証明せよ
図形の性質 図形の性質の基本②【中学受験のドラえもんがていねいに解説】
単元:
#数A#図形の性質#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形ABCの内心をIとし、3辺BC、CA、ABに関してIと対称な点をそれぞれP,Q,Rとする。Iは三角形PQRについてどのような点か?
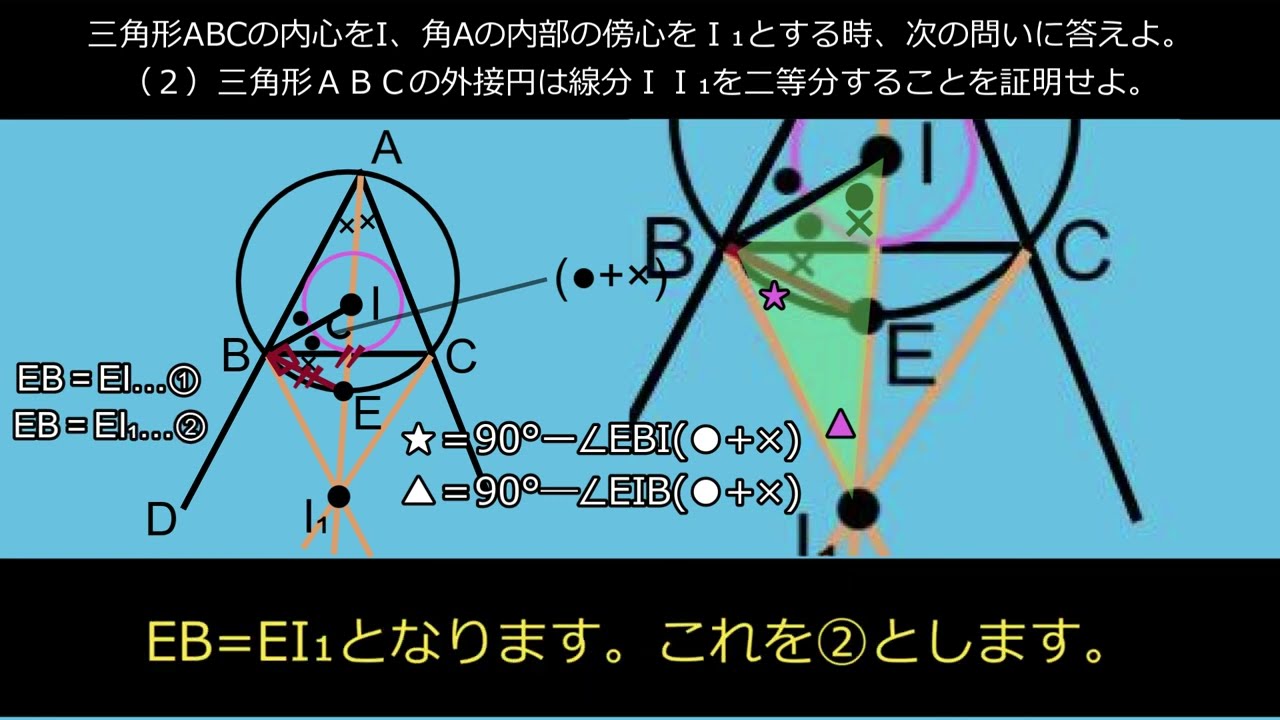
三角形ABCの内心をI、角Aの内部の傍心をI₁とする時、次の問いに答えよ。
(1)角IBI₁の大きさを求めよ。
(2)三角形ABCの外接円は線分II₁を二等分することを証明せよ。
AB=ACである二等辺三角形ABCの頂点Aから辺BCに下ろした垂線をADとする。
角Bの内部の傍接円IBの半径はADに等しいことを証明せよ。
この動画を見る
三角形ABCの内心をIとし、3辺BC、CA、ABに関してIと対称な点をそれぞれP,Q,Rとする。Iは三角形PQRについてどのような点か?
三角形ABCの内心をI、角Aの内部の傍心をI₁とする時、次の問いに答えよ。
(1)角IBI₁の大きさを求めよ。
(2)三角形ABCの外接円は線分II₁を二等分することを証明せよ。
AB=ACである二等辺三角形ABCの頂点Aから辺BCに下ろした垂線をADとする。
角Bの内部の傍接円IBの半径はADに等しいことを証明せよ。
場合の数 集合の個数~ベン図も使えます~【さこすけ's サイエンスがていねいに解説】
単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
全体集合Uと,その部分集合A,Bに対して$n(U)=50,n(A∪B)=42,n(A∩B)=3,
n$($A$の補集合$∩B)=15$であるとき、次の集合の要素の個数を求めよ。
(1)$A$の補集合$∩B$の補集合 (2)$A∩B$の補集合 (3)$A$
500以上1000以下の整数のうち,次のような数は何個あるか。
(1)11の倍数でない整数 (2)11の倍数であるが3の倍数でない整数
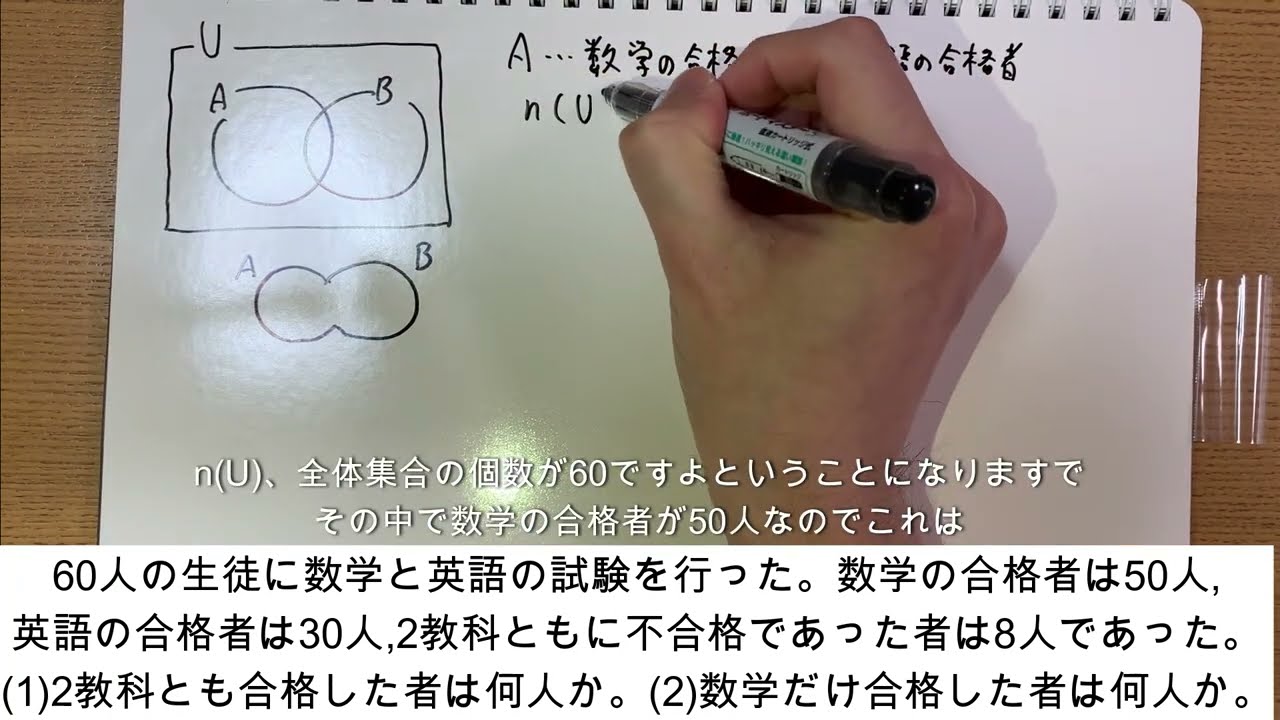
60人の生徒に数学と英語の試験を行った。数学の合格者は50人,
英語の合格者は30人,2教科ともに不合格であった者は8人であった。
(1)2教科とも合格した者は何人か。(2)数学だけ合格した者は何人か。
この動画を見る
全体集合Uと,その部分集合A,Bに対して$n(U)=50,n(A∪B)=42,n(A∩B)=3,
n$($A$の補集合$∩B)=15$であるとき、次の集合の要素の個数を求めよ。
(1)$A$の補集合$∩B$の補集合 (2)$A∩B$の補集合 (3)$A$
500以上1000以下の整数のうち,次のような数は何個あるか。
(1)11の倍数でない整数 (2)11の倍数であるが3の倍数でない整数
60人の生徒に数学と英語の試験を行った。数学の合格者は50人,
英語の合格者は30人,2教科ともに不合格であった者は8人であった。
(1)2教科とも合格した者は何人か。(2)数学だけ合格した者は何人か。
福田の数学〜慶應義塾大学2023年医学部第3問〜接線が作る三角形

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#三角形の辺の比(内分・外分・二等分線)#図形と方程式#微分法と積分法#軌跡と領域#接線と増減表・最大値・最小値#関数と極限#微分とその応用#積分とその応用#数列の極限#微分法#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 座標平面上の曲線y=$\frac{1}{x^2}$ (x $\ne$ 0)をCとする。$a_1$を正の実数とし、点$A_1$$\left(a_1, \frac{1}{a_1^2}\right)$におけるCの接線を$l_1$とする。$l_1$とCの交点で$A_1$と異なるものを$A_2$$\left(a_2, \frac{1}{a_2^2}\right)$とする。次に点$A_2$におけるCの接線を$l_2$とCの交点で$A_2$と異なるものを$A_3$$\left(a_3, \frac{1}{a_3^2}\right)$とする。以下、同様にしてn=3,4,5,...に対して、$A_n$$\left(a_n, \frac{1}{a_n^2}\right)$におけるCの接線を$l_n$とし、$l_n$とCの交点で$A_n$と異なるものを$A_{n+1}$$\left(a_{n+1}, \frac{1}{a_{n+1}^2}\right)$とする。
(1)$\frac{a_2}{a_1}$=$\boxed{\ \ あ\ \ }$であり、$\frac{a_3}{a_1}$=$\boxed{\ \ い\ \ }$である。
(2)$a_n$を$a_1$で表すと$a_n$=$\boxed{\ \ う\ \ }$である。無限級数$\displaystyle\sum_{n=1}^{\infty}a_n$の和をTを$a_1$を用いて表すとT=$\boxed{\ \ え\ \ }$である。
(3)$a_1$を正の実数すべてにわたって動かすとき、三角形$A_1A_2A_3$の重心が描く軌跡の方程式をy=f(x)の形で求めるとf(x)=$\boxed{\ \ お\ \ }$となる。
(4)三角形$A_1A_2A_3$が鋭角三角形になるための条件は$\boxed{\ \ か\ \ }$<$a_1$<$\boxed{\ \ き\ \ }$である。
(5)x軸上に2点$A'_1$($a_1$, 0), $A'_2$($a_2$, 0)をとり、台形$A_1A_2A'_2A'_1$の面積を$S_1$とする。また、点$A_1$から点$A_3$にいたる曲線Cの部分、および線分$A_3A_2$と$A_2A_1$で囲まれた図形の面積を$S_2$とする。このとき、$S_1$:$S_2$=$\boxed{\ \ く\ \ }$:$\boxed{\ \ け\ \ }$である。ただし、$\boxed{\ \ く\ \ }$と$\boxed{\ \ け\ \ }$は互いに素な自然数である。
2023慶應義塾大学医学部過去問
この動画を見る
$\Large\boxed{3}$ 座標平面上の曲線y=$\frac{1}{x^2}$ (x $\ne$ 0)をCとする。$a_1$を正の実数とし、点$A_1$$\left(a_1, \frac{1}{a_1^2}\right)$におけるCの接線を$l_1$とする。$l_1$とCの交点で$A_1$と異なるものを$A_2$$\left(a_2, \frac{1}{a_2^2}\right)$とする。次に点$A_2$におけるCの接線を$l_2$とCの交点で$A_2$と異なるものを$A_3$$\left(a_3, \frac{1}{a_3^2}\right)$とする。以下、同様にしてn=3,4,5,...に対して、$A_n$$\left(a_n, \frac{1}{a_n^2}\right)$におけるCの接線を$l_n$とし、$l_n$とCの交点で$A_n$と異なるものを$A_{n+1}$$\left(a_{n+1}, \frac{1}{a_{n+1}^2}\right)$とする。
(1)$\frac{a_2}{a_1}$=$\boxed{\ \ あ\ \ }$であり、$\frac{a_3}{a_1}$=$\boxed{\ \ い\ \ }$である。
(2)$a_n$を$a_1$で表すと$a_n$=$\boxed{\ \ う\ \ }$である。無限級数$\displaystyle\sum_{n=1}^{\infty}a_n$の和をTを$a_1$を用いて表すとT=$\boxed{\ \ え\ \ }$である。
(3)$a_1$を正の実数すべてにわたって動かすとき、三角形$A_1A_2A_3$の重心が描く軌跡の方程式をy=f(x)の形で求めるとf(x)=$\boxed{\ \ お\ \ }$となる。
(4)三角形$A_1A_2A_3$が鋭角三角形になるための条件は$\boxed{\ \ か\ \ }$<$a_1$<$\boxed{\ \ き\ \ }$である。
(5)x軸上に2点$A'_1$($a_1$, 0), $A'_2$($a_2$, 0)をとり、台形$A_1A_2A'_2A'_1$の面積を$S_1$とする。また、点$A_1$から点$A_3$にいたる曲線Cの部分、および線分$A_3A_2$と$A_2A_1$で囲まれた図形の面積を$S_2$とする。このとき、$S_1$:$S_2$=$\boxed{\ \ く\ \ }$:$\boxed{\ \ け\ \ }$である。ただし、$\boxed{\ \ く\ \ }$と$\boxed{\ \ け\ \ }$は互いに素な自然数である。
2023慶應義塾大学医学部過去問
福田の数学〜慶應義塾大学2023年医学部第2問〜反復試行の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ nを自然数とする。A君とB君の2人が以下の試合Tをnセット行い、それぞれが得点をためていくとする。
試合T:2人で腕ずもうを繰り返し行う。毎回、A君, B君のどちらも勝つ確率は$\frac{1}{2}$ずつである。どちらかが先に2勝したら、腕ずもうを行うのをやめる。2勝0敗の者は2点を、2勝1敗の者は1点を得る。2勝しなかった者の得点は0点である。
A君が1セット目からnセットまでに得た点の合計を$a_n$とし、B君が1セット目からnセットまでに得た点の合計を$b_n$とする。
(1)n=1とする。$a_1$=2である確率は$\boxed{\ \ あ\ \ }$であり、$a_1$=1である確率は$\boxed{\ \ い\ \ }$である。
(2)n≧4とする。試合Tをnセット行ううち、A君が2点を得るのがちょうど2セット、かつ1点を得るのがちょうど2セットである確率は$\frac{\boxed{\ \ う\ \ }}{\boxed{\ \ え\ \ }}$である。
(3)n≧2とする。$a_n$=$n$+2かつ$b_n$=0である確率は$\frac{\boxed{\ \ お\ \ }}{\boxed{\ \ か\ \ }}$である。
(4)$a_n$=2である確率は$\frac{\boxed{\ \ き\ \ }}{\boxed{\ \ く\ \ }}$である。
(5)n=4とする。$a_4$>$b_4$である確率は$\frac{\boxed{\ \ け\ \ }}{\boxed{\ \ こ\ \ }}$である。
2023慶應義塾大学医学部過去問
この動画を見る
$\Large\boxed{2}$ nを自然数とする。A君とB君の2人が以下の試合Tをnセット行い、それぞれが得点をためていくとする。
試合T:2人で腕ずもうを繰り返し行う。毎回、A君, B君のどちらも勝つ確率は$\frac{1}{2}$ずつである。どちらかが先に2勝したら、腕ずもうを行うのをやめる。2勝0敗の者は2点を、2勝1敗の者は1点を得る。2勝しなかった者の得点は0点である。
A君が1セット目からnセットまでに得た点の合計を$a_n$とし、B君が1セット目からnセットまでに得た点の合計を$b_n$とする。
(1)n=1とする。$a_1$=2である確率は$\boxed{\ \ あ\ \ }$であり、$a_1$=1である確率は$\boxed{\ \ い\ \ }$である。
(2)n≧4とする。試合Tをnセット行ううち、A君が2点を得るのがちょうど2セット、かつ1点を得るのがちょうど2セットである確率は$\frac{\boxed{\ \ う\ \ }}{\boxed{\ \ え\ \ }}$である。
(3)n≧2とする。$a_n$=$n$+2かつ$b_n$=0である確率は$\frac{\boxed{\ \ お\ \ }}{\boxed{\ \ か\ \ }}$である。
(4)$a_n$=2である確率は$\frac{\boxed{\ \ き\ \ }}{\boxed{\ \ く\ \ }}$である。
(5)n=4とする。$a_4$>$b_4$である確率は$\frac{\boxed{\ \ け\ \ }}{\boxed{\ \ こ\ \ }}$である。
2023慶應義塾大学医学部過去問
気付けば一瞬!! 気付けば爽快!! 中学数学

【整数問題】考えられる候補は何パターンだろうか【慶應義塾大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$6a^{3}+11a^{2}b^{2}c+3ab^{3}c$=6270を満たす(a,b,c)の組をすべて求めよ。
ただし、a,b,cはそれぞれ2以上の整数とする。
慶應義塾大過去問
この動画を見る
$6a^{3}+11a^{2}b^{2}c+3ab^{3}c$=6270を満たす(a,b,c)の組をすべて求めよ。
ただし、a,b,cはそれぞれ2以上の整数とする。
慶應義塾大過去問
一工夫必要な不定方程式

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数(a,b)の組は何組あるか?
$3ab+4a-b=684$
この動画を見る
自然数(a,b)の組は何組あるか?
$3ab+4a-b=684$
典型的な整数問題!!日大習志野

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$ab+2a+2b =41$のとき
2つの自然数$a,b$を求めよ。($1<a<b$)
日本大学習志野高等学校
この動画を見る
$ab+2a+2b =41$のとき
2つの自然数$a,b$を求めよ。($1<a<b$)
日本大学習志野高等学校
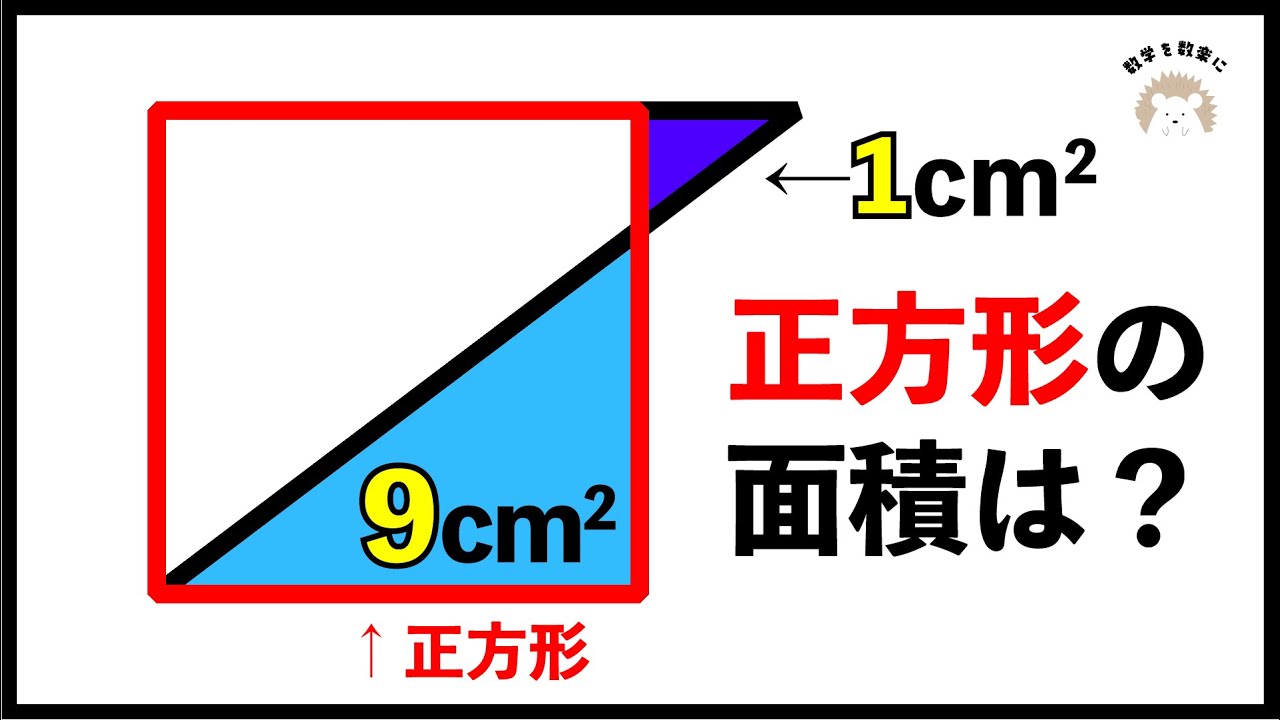
三角形を台形として考える 正方形と面積比
大学入試問題#518「2024年の整数問題はこれで決まり!!」 英語orドイツ語 #整数問題
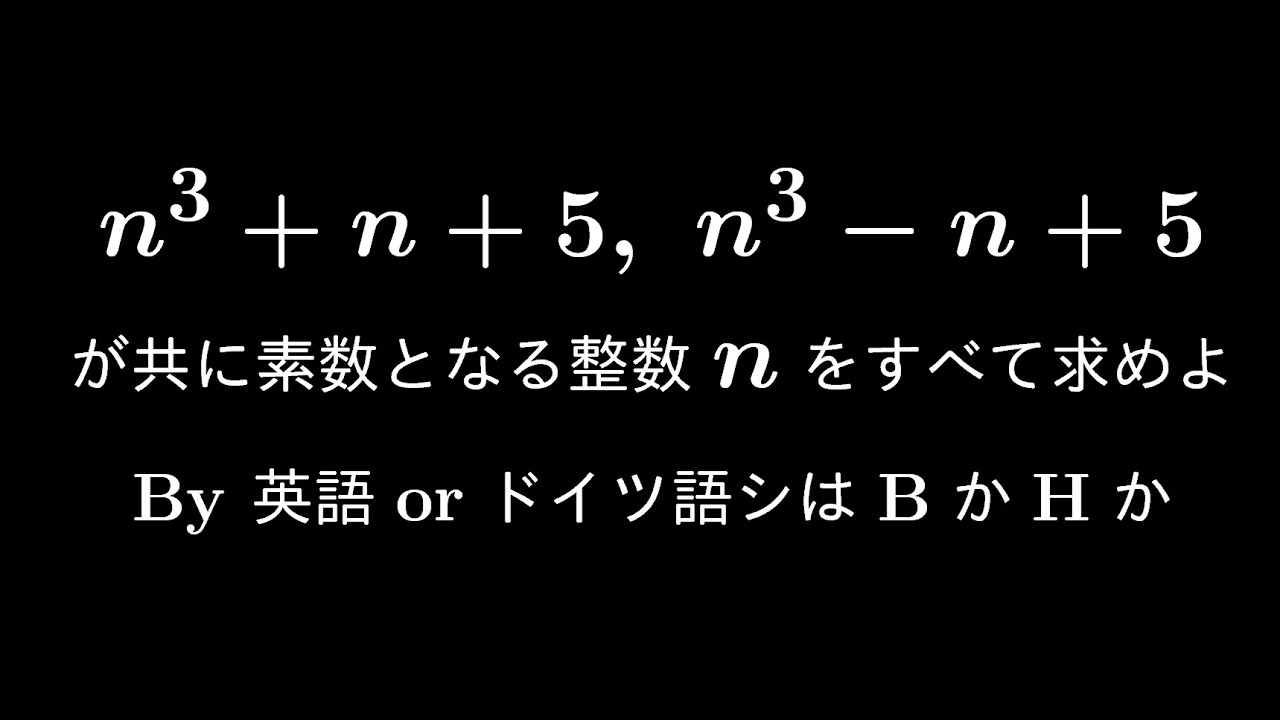
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$n^3+n+5$
$n^3-n+5$
が共に素数となるような整数$n$を求めよ
この動画を見る
$n^3+n+5$
$n^3-n+5$
が共に素数となるような整数$n$を求めよ
千葉大 整数解を持つ条件

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
Pは素数であり,
$P^2+(5-P^2)x-3P=0$が整数解をもつのは$P=2$に限ることを示せ.
千葉大過去問
この動画を見る
Pは素数であり,
$P^2+(5-P^2)x-3P=0$が整数解をもつのは$P=2$に限ることを示せ.
千葉大過去問
大学入試問題#517「どこでも解説されてる良問」 京都大学(2018) #整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$n^3-yn+9$が素数となるような整数$n$をすべて求めよ。
出典:2018年京都大学 入試問題
この動画を見る
$n^3-yn+9$が素数となるような整数$n$をすべて求めよ。
出典:2018年京都大学 入試問題
【ガチ良問】素数が絡んだ整数問題の難問です【数学】

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
pを素数,kを自然数とする。
$12p^{2}+12p+1=k^{2}$を満たすようなpの値を求めよ。
この動画を見る
pを素数,kを自然数とする。
$12p^{2}+12p+1=k^{2}$を満たすようなpの値を求めよ。
場合の数 集合の基本~ベン図を描こう~【さこすけ's サイエンスがていねいに解説】

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$U={1,2,3,4,5,6,7,8,9}$を全体集合とする。Uの部分集合A,Bについて、
$A∩B={2}$,(Aの補集合)$∩B={2,4,6,8}$,(Aの補集合)$∩$(Bの補集合)$={1,9}$であるとき、次の集合を求めよ。
(1)$A∪B$ (2)$B$ (3)$A∩$(Bの補集合)
U={$x\vert 1\leqq x\leqq 10$,xは整数}を全体集合とする。Uの部分集合
$A={1,2,3,4,8},B={3,4,5,6},C={2,3,6,7}$について、次の集合を求めよ。
(1)$A∩B∩C$ (2)$A∪B∪C$ (3)$A∩B∩$(Cの補集合) (4)(Aの補集合)$∩B∩$(Cの補集合) (5)($A∩B∩C$の補集合) (6)$(A∪C)∩$(Bの補集合)
$A={1,3,3a-2},B={-5,a+2,a^2-2a+1},A∩B={1,4}$のとき、
定数aの値と和集合$A∪B$を求めよ
この動画を見る
$U={1,2,3,4,5,6,7,8,9}$を全体集合とする。Uの部分集合A,Bについて、
$A∩B={2}$,(Aの補集合)$∩B={2,4,6,8}$,(Aの補集合)$∩$(Bの補集合)$={1,9}$であるとき、次の集合を求めよ。
(1)$A∪B$ (2)$B$ (3)$A∩$(Bの補集合)
U={$x\vert 1\leqq x\leqq 10$,xは整数}を全体集合とする。Uの部分集合
$A={1,2,3,4,8},B={3,4,5,6},C={2,3,6,7}$について、次の集合を求めよ。
(1)$A∩B∩C$ (2)$A∪B∪C$ (3)$A∩B∩$(Cの補集合) (4)(Aの補集合)$∩B∩$(Cの補集合) (5)($A∩B∩C$の補集合) (6)$(A∪C)∩$(Bの補集合)
$A={1,3,3a-2},B={-5,a+2,a^2-2a+1},A∩B={1,4}$のとき、
定数aの値と和集合$A∪B$を求めよ
